Trans. Nonferrous Met. Soc. China 22(2012) 139-146
Thermo-Calc and T-fS-CL coupling based method to determine solidification paths of alloys solidified under condition of Biot
0.1
Zhao Guang-wei1, LI Xin-zhong1, XU Da-ming1, GUO Jing-jie1, FU Heng-zhi1, DU Yong2, HE Yue-hui2
1. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
Received 25 March 2011; accepted 12 July 2011
Abstract:
A binary continuum model for dendritic solidification transport phenomena and corresponding numerical algorithm for the strong nonlinear coupling of T-fS-CL were extended to multicomponent alloys solidified under condition of Biot?0.1. Based on the extended model/algorithm, a method considering heat transfer was proposed to predict the solidification paths and microsegregation of alloys solidified under the same condition. The new algorithm and method were closely coupled with the commercial Thermo-Calc package via its TQ6-interface codes for instantaneous determination of the related thermodynamic data at each calculation time step. The sample simulation performed on an Al-2Si-3Mg alloy system indicates the availability and reliability of the model/algorithm and the proposed method for predicting solidification paths and microsegregation. Computional and experimental investigations on an Al-5.17Cu-2.63Si ternary alloy were conducted, and a reasonable agreement between the computation and experiment was obtained.
Key words:
thermo-calc; solidification transport; solidification paths; microsegregation;
1 Introduction
Conventional alloy development, especially for multicomponent alloys such as the high speed tool alloys (Fe-C-Cr-W-Mo-V-Co) [1], is costly and time consuming because it involves casting and analyzing a series of specimens. Further more, most of the metallic industry alloys are multicomponent and solidified in a dendritic form with the formation of microsegregation and several kinds of secondary phases [2, 3]. The degree of the microsegregation and the types and amounts of the secondary phases may significantly impact the mechanical properties of the solidified alloy materials both at room and working temperatures [4, 5]. Therefore, accurate prediction of the solidification paths and microsegregation of multicomponent alloys under a given solidification condition is critical in optimizing the composition and processing parameters in new alloys development [6]. The analyses of solidification of multi-component alloys are much more difficult than binary alloys because of the lack of phase-diagram information [7]. Fortunately, the use of thermodynamic calculation tools, such as the Calphad approach [8], clearly appears to be the appropriate method for multi-component systems.
It is known from heat transfer knowledge that the Biot number is a dimensionless number used for non-steady-state heat transfer calculations [9]. It is defined as Biot=hl/k, where h represents the heat transfer coefficient; l is the characteristic length which is commonly defined as the volume of the body divided by the surface area of the body and k is the thermal conductivity of the body. When the value of the Biot number is smaller than 0.1, the heat conduction inside the body is much faster than the heat convection away from its surface, and the temperature gradient inside the body is negligible [10].
In this work, a binary continuum model for dendritic solidification transport phenomena [11] and the corresponding numerical algorithm for the strong nonlinear coupling of T-fS-CL [12] were extended to multicomponent alloys solidified under a heat-transfer condition of Biot?0.1. Based on the extended model or algorithm, a method was proposed for predicting the solidification paths and microsegregation of the alloys solidified under the condition of Biot?0.1. The new algorithm and method were closely coupled with the commercial Thermo-Calc package [13] via its TQ6-interface codes, for instantaneous determination of the related thermodynamic data at each calculation time step. This method can be used for predicting the alloy solidification behaviors of the thermal analysis cups used for the developments/analyses of the alloys [14], the suspended droplets [15], and especially the alloy specimens for DTA, DSC and single pan scanning calorimeter [16]. All the solidification cases mentioned above have a similar feature, i.e., the volumes of the alloy specimens are small [17] and can easily satisfy the heat-transfer condition of Biot?0.1 (i.e. a simultaneously bulk solidification occurs).
2 Model description
A previously proposed continuum model for dendritic solidification phenomenon of binary alloys [11] was adopted and revised for multicomponent alloys, which can be described by the following governing equations.
1) Solidification heat energy transfer:
(1)
where ρm, ρL and ρS represent the density of the mushy zones, liquid phase and solid phase, respectively; cpm, cpL and cS represent the specific heat capacity of the mushy zones, liquid phase and solid phase, respectively; cp is the specific heat capacity of the alloy; λm represents the thermal conductivity of the mushy zones; t represents time and fS represents the volume fraction of solid phase.
2) Solidification species mass transfer for the nth component:
(2)
where Cnm, CnL and CnS represent the composition of the mushy zones, liquid phase and solid phase, respectively; DnL and DnS represent the diffusion coefficients of solute in liquid phase and solid phase, respectively.
3) L-S phase-change characteristic function for a specific multicomponent alloy:
(3)
4) Solidification mass conservation:
(4)
5) Momentum transfer for bulk/interdendritic liquid flow:
(5)
where T, C, fL and v represent the macroscopic fields (on an ingot/casting length-scale) of temperature, composition, volumetric fraction and velocity vector of liquid phase in the solidification process of a multicomponent alloy, respectively; μ presents the dynamic viscosity and K represents the permeability coefficient of mushy zones.
When Biot?0.1 for an alloy specimen, the internal temperature distribution in the sample is assumed to be uniform, and the whole specimen can be treated as a close system [18]. Then the continuum transfer model of Eqs. (1)-(5) can be expressed as the following form for a ternary alloy specimen when neglecting the weak macroscopic liquid flow.
Heat transfer equation:
(6)
where ρ is the density; he represents the equivalent heat transfer coefficient between the alloy specimen body and the environmental cooling medium; h is the latent heat of the alloy; V and S represent the volume and the surface area of the specimen body investigated, respectively; TR represents the room temperature and fS is the volume of fraction solid phase in the alloy specimen.
The entire alloy specimen is isolated in the material from the surrounding during cooling down, i.e. in a close solidification case, and then the solute mass balances can be expressed as:
(7)
where Cn0 and ρ0 represent the initial composition and density of the liquid phase; η represents a volume fraction variable concentration within solidifying dendrites.
Equation (7) is equivalent to
(8)
In the computation process, the liquidus temperature of the solidifying multicomponent alloy can be calculated by calling the related database COST2 and the interface program TQ6 of Thermo-Calc software at each time step according to the corresponding liquid compositions 
as:
(9)
where TL represents the liquidus corresponding to the current composition.
3 Numerical procedure
It is known that the three variables of temperature, solid fraction and liquid composition, i.e. T-fS-CL, are strongly nonlinear coupled during solidification of the alloy, and a numerical method to solve this coupling is proposed with the consideration of any solid back diffusion (SBD) in a binary dendrite solidification problem [12]. This solution method could be extended to multicomponent alloys, and directly linked with a thermodynamics database COST2 and the interface program TQ6 of a Thermo-Calc software package [13].
An explicit finite difference scheme is used to obtain the numerical solution of the strongly coupled alloy solidification problem. Omitting the latent heat term temporarily, Eq. (6) can be expressed as:
(10)
where R is the radius of the alloy specimen.
Discreting Eq. (10) and assuming 
and 
in a time interval 
, the numerical equation for calculating the temperature Ti+1 at time ti+1 can be calculated as:
(11)
where
The species mass formulation of Eq. (8) may represent a general microsegregation model when taking a differential form but in a mixture-averaged or statistical-average sense. According to the micro/ macrosegregation modeling proposed in Refs. [19, 20], Equation (8) can be rewritten for a closed single-phase α(Al), the multicomponent solidification
(12)
In this general microsegregation model of Eq.(12), the unified SBD-parameters for the nth-solute can be expressed as:
(13)
where the non-dimensional parameters of φn and θn can be written accordingly as:
(14)
and
(15)
which represent the sensibility of interdendritic liquid-concentration to the SBD-behaviors and the Fourier diffusion number with a dendrite-geometry modification for the nth-solute, respectively. Where Rf represents the solidification rate; β represents the solidification shrinkage, respectively; A2N and ζ represent a basic geometry-unit vector and a normalized weighting vector corresponding to the basic geometry-units A2N, respectively. The parameters kn and DnS represent the solute partition coefficients and the solid diffusion coefficients for the nth solute, respectively.
Now, the solidification of a typical ternary eutectic solidification-path is taken as example, i.e. 
the corresponding liquid concentrations can be calculated by the following equations for each corresponding solidification stage (the subscripts 2E and 3E represent binary and ternary eutectic solidification, respectively).
In the stage of single-solution solidification, e.g. α(Al):
(16)
where
and CF1=(fLρL)i+1+
.
For binary eutectic solidification:
(17)
where
(18)
(19)
(20)
(21)
(22)
where parameters Φn(2E), φn(2E), θn(2E), kn(2E) and DnS(2E) of the two phases eutectic solidification stage have the same meanings with Φn, φn, θn, kn and DnS of the single-solution solidification, respectively. The symbols of 
and 
denote the critical solid-fractions at which the solidification transitions of 
and 
occur, respectively.
In the process of the ternary eutectic solidification, the liquid concentrations for the both two solutes have to keep constant according to Gibbs phase rule, i.e.,
(23)
As Eq. (11) is derived without considering latent heat temporarily, the temperature Ti+1 calculated by Eq. (11) only represents the decreased value due to the heat loss by conduction/convection in the time interval 
According to the temperature- compensation method [21], the solidification temperature at time ti+1 is the liquidus temperature 
, while the latent heat released by the solid phase formed in 
is equal to the heat capacity of the temperature difference between the liquidus temperature and the temperature calculated by Eq. (11), i.e. 
. Based on the principle of heat energy balance and the assumption of local thermodynamic equilibrium solidification, the numerical formula for the solid fraction increase in the time interval can be derived as:
(24)
Although the solid fraction 
of time ti+1 can be calculated by Eq. (24), it can be seen from Eqs. (11), (16) and (17) that, the calculation of Ti+1 and 
needs the value of . As mentioned above, the solid fraction increase , the temperature 
and the liquid composition are strongly coupled and there must be a local balance among them at time ti+1, which means they need to be solved at the same time. Based on the above argument, the following iteration procedure directly coupled with a thermodynamics database COST2 and the interface program TQ6 of Thermo-Calc software package is proposed to obtain the solution to the T-fS-CL coupling.
1) The initial value of is set equal to zero (
) and the approximation of Ti+1 is calculated using Eq. (11).
2) The approximations of Ti+1, 
and 
are used as the initial values of temperature and compositions at time ti+1 (T1=Ti+1, 
and 
, respectively), the approximate compositions of 
and 
are calculated using Eqs. (16) and (17).
3) The approximate compositions of and are used, and the TQ6-interface program and the related database COST2 of Thermo-Calc are called to calculate the liquidus temperature and other thermodynamic parameters such as the solute partition coefficient.
4) The approximation of solidification increase is calculated by Eq. (24) and the average is taken 
.
5) The new approximation of is calculated with new initial values of F1 using Eq. (11), 
and 
, 
.
6) With the new initial values of T1, F1, CB1 and CC1, the new initial approximations of and are calculated by Eqs.(16) and (17), and 
and 
are taken;
7) All the following conditions are judged if they are true:
where εF, εT, εB1 and εC1 are the predefined convergence accuracies for the iterations of the solid fraction, temperature and compositions of solutes B and C, respectively. If the conditions are not true, the liquidus temperature is calculated using CB1 and CC1 via calling Thermo-Calc and steps (4)-(7) are repeated until all the above accurate conditions are satisfied.
4 Sample calculations of Al-2Si-3Mg alloy
To investigate the feasibility of the model and algorithm coupled with the ThermoCalc/databases, sample calculations are carried out on an Al-2Si-3Mg alloy. The solidification paths and T-fS curves are calculated under five assumed solidification conditions with the legends of lever-rule, he=20 (unit: W/(m2·K) and similarly hereinafter), he=476.46t-0.45, he=200 and Scheil model. These legends represent the limiting solidification case of fully equilibriums in both the solid and liquid phases, and in a relative real solidification mode, as described/calculated by Eqs. (6)-(24), with the heat transfer coefficient he valves of 20, 476.46t-0.45 and 200, and in another limiting case of complete non-solidification for both solute Si and Mg, respectively. Under the third condition, the heat transport coefficient is obtained by fitting the inversely calculated data of heat transfer coefficient for the sand mold to power function form which is the same to that in Ref. [22].
Figure 1(a) shows the calculated solidification paths and Fig. 1(b) shows the temperature vs solid fraction curve of Al-2Si-3Mg alloy under the assumed different solidification conditions. It can be seen from Fig. 1(a) that the solidification path of the Scheil model is (L→α)→(L→α+Si)→(L→α+Si+Mg2Si), while the solidification paths under the other four conditions finished on the binary trough (L→α)→(L→α+Si). It can be also seen from the temperature vs solid fraction (T-fS) curve shown in Fig. 1(b) that only the solidification path of Scheil model reaches the ternary eutectic point and with the volume fractions of 21.69% and 5.77% form binary and ternary eutectic phases, respectively. Under other conditions of Lever-rule, he=20, he=476.46t-0.45 and he=200, the solidification paths end on the binary eutectic trough at temperatures of 581.40, 580.06, 578.38 and 571.73 °C, respectively, and with the binary eutectic formed volume fraction of 23.13%, 24.87%, 26.13% and 26.80%, respectively. It can be seen that the influence of heat transfer coefficient on the solidification path is obviously. For the present Al-Si-Mg alloy, the greater the heat coefficient is, the closer the solidification path is to the predicted results by Scheil model. On the contrary, the solidification path is closer to the lever-rule model.
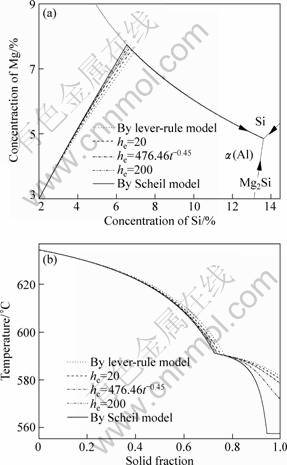
Fig. 1 Sample calculation of solidification paths (a) and temperature solid fraction (T-fs) curves (b) of Al-2Si-3Mg alloy under different solidification conditions (Limiting case of Lever-rule refers to ΦMg=ΦSi=1 and Scheil to ΦMg=ΦSi=0)
5 Experimental verification
5.1 Experimental process and results
To further investigate the reliability of the present model and algorithm, a solidification experiment of Al-Cu-Si ternary alloy is carried out. The experimental material of Al-5.17Cu-2.63Si was prepared with pure Al(99.7%), Al-49.2Cu and Al-12.7Si master alloys by ingot metallurgy in a graphite crucible in a resistance furnace. The alloy composition was analyzed chemically using samples taken from different locations of the specimens. The mold was made of sodium silicate sand. The dimensions of the specimen are shown in Fig. 2. In the pouring and solidification processes, the cooling curves were recorded using calibrated K-type thermocouples, which were linked to a PC-computer controlled data-acquisition module of ECON series (Data Translation, Inc., USA).
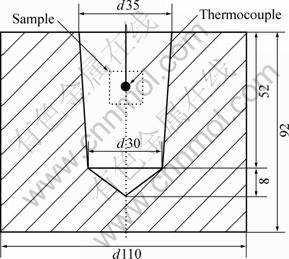
Fig. 2 Dimensions of sample (Unit: mm)
It can be seen from Fig. 3(a) that the solidification of the alloy experiences three stages including single phase solidification, binary eutectic solidification and the final ternary eutectic solidification, respectively. Figure 4 shows the BSE image of the solidified specimen (near the thermocouples, see Fig. 2) captured by a Hitachi S-4700 scanning electron microscope (SEM). As marked on the BSE image, the gray area is α(Al), the light gray area is Si phase of the divorced binary eutectic, and the rest is ternary eutectic including α(Al), Si and θ phases. The image was used for measurements of the amounts of phases formed in each solidification stage.
The function of the equivalent heat transfer coefficient between the casting and mold is determined using an inverse calculation technique [23, 24] via the present simulation program. In the inverse calculation process, the interface heat transfer coefficient is adjusted to insure the simulated cooling curves coincide with the measured values. Figure 3(a) also shows the comparison of the final determined cooling curve (the solid line) with the measured data for the sand mold alloy specimen. It can be seen from the heat transfer coefficient curves of Fig. 3(b) that the heat transfer coefficient reduces steeply in the first 50 s after pouring/solidification and then tends to be stable.
Fig. 3 Comparison of measured and simulated cooling curves (a) and corresponding heat transfer coefficient (b) for Al-5.17Cu-2.63Si specimen solidified in sand mold
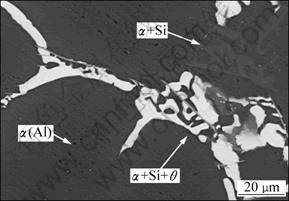
Fig. 4 BSE image of Al-5.17Cu-2.63Si alloy solidified in sand mold
5.2 Results and discussion
The thermal conductivity of Al alloy is normally k=100-300 W/(m·K) [10], the heat transfer coefficient and characteristic length of the specimen in this work are he=30-250 W/(m2·K) (see Fig.3(b)) and l=15-17.5 mm. According to the equation of 
, the Biot number in the present study is Biot=(0.0015-0.04375)< 0.1. Therefore, the model/algorithm and method proposed above are applicable to calculate the solidification paths and microsegregation of the specimen.
Figures. 5(a) and (b) show the calculated solidification path and the temperature vs solid fraction curve of the specimen, including the calculation results for the two limit models of lever-rule (i.e. 
) and Scheil model (i.e. ). It can be seen from Fig. 5(a) that the solidification path of the alloy runs down the liquidus surface from initial composition until the binary trough of L→α+Si, and reaches the ternary eutectic point of L→α+Si+θ at the end of the solidification for all the three cases, i.e. the present solidification path is (L→α)→(L→α+Si)→ (L→α+Si+θ) which is the same with the experimental results. From the temperature vs solid fraction curves shown in Fig. 5(b), it can be seen that the solidification path of the specimen meets the binary trough at 541.2 °C with volume fraction of 77.85% formed as the primary phase, and reaches the ternary eutectic point at 512.1 °C with volume fraction of 9.09% formed as ternary eutectic (α+Si+θ) and the remainder is the binary eutectic (α+Si).
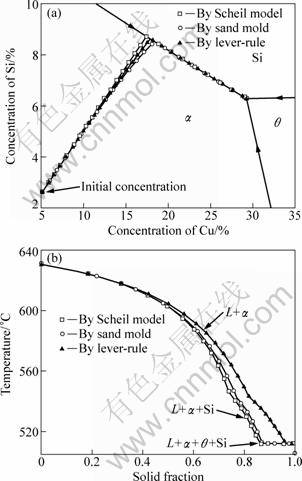
Fig. 5 Calculated solidification paths (a) and temperature vs solid fraction curves (b) of Al-5.17Cu-2.63Si alloy specimens solidified in sand mold and under different limiting solidification cases
Quantitative analysis of the microstructure is carried out using an image analysis software (Image-Pro Plus 6.0). As the atomic number of Al and Si is neighboring, it is difficult to accurately distinguish α(Al) and Si-phase by the analysis software because of the almost same contrast in the BSE image. In the present work, the image-fractions for the primary phases (α) and binary eutectic (α+Si) are counted together as a combined phase of (α+Si), and the remainder is ternary eutectic (α+Si+θ). Figure 6 shows the comparison of volume fractions for the different phases between the calculated and measured results. It can be seen that the calculated results for the present experimental conditions are reasonably agreeable to the measured results.
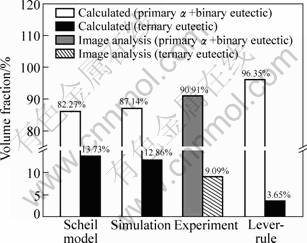
Fig. 6 Comparison of volume fractions of phases between calculated and measured results of different solidification stages of Al-5.17Cu-2.63Si alloy solidified in sand mold
It can be seen from the above sample calculations and experiment that the present model and algorithm for the prediction of the solidification paths and microsegregation of alloys solidified under the condition of Biot?0.1 are feasible and reliable. This method can be used for the analysis of any alloy solidified under the condition of Biot?0.1 in principle. As the volumes of the specimens of DTA, DSC and SPTA are small and can easily satisfy the condition of Biot?0.1, the present technique may be used for providing additional information for the solidification paths and microsegregation of an alloy for new alloy developments instead of an experimental investigation.
6 Conclusions
1) A binary continuum model for dendritic solidification transport phenomena and the corresponding numerical algorithm for the strong nonlinear coupling of T-fS-CL are extended to a multicomponent alloys solidified under the condition of Biot?0.1. Based on the extended model and algorithm, a method considering heat transfer is proposed to predict the solidification paths and microsegregation of alloys solidified under the same condition.
2) The new algorithm and method are closely coupled with the commercial Thermo-Calc package via its TQ6-interface codes, for instantaneous determination of the related thermodynamic data at each calculation time step.
3) The availability and reliability of the proposed multicomponent/multiphase model and algorithm for predicting the solidification paths and microsgregation are demonstrated by sample calculations with Al-2Si-3Mg specimens solidified under different heat transfer conditions, and by comparing the results between computations and the corresponfing experimental investigations with Al-5.17Cu-2.63Si ternary alloy.
References
[1] Boccalini M, Goldenstein H. Solidification of high speed steels [J]. Int Mater Reviews, 2001, 46(2): 92-113.
[2] Battle T P. Mathematical modeling of solute segregation in solidifying materials [J]. Int Materials Reviews, 1992, 37(6): 249-270.
[3] Kattamis T Z, Flemings M C. Dendrite morphology, microsegregation, and homogenization of low-alloy steel [J]. Transactions of the Metallurgical Society of AIME, 1965, 233(5): 992-999.
[4] Cahoon J R, Paxton H W. The mechanical properties of some unidirectionally solidified aluminum alloys: part I: Room temperature properties [J]. Transactions of the Metallurgical Society of AIME, 1969, 245(7): 1401-1409.
[5] Won Y M, Yeo T J, Seol D J, Oh K H. A new criterion for internal crack formation in continuously cast steels [J]. Metallurgical and Materials Transactions B, 2000, 31(4): 779-794.
[6] Kraft T, Rettenmayr M, Exner H E. Modeling of dendritic solidification for optimizing casting and microstructure parameters [J]. Progress in Materials Science, 1997, 42(1-4): 277-286.
[7] Chang Y A, CHEN Shuang-lin, ZHANG Fan, YAN Xin-yan, XIE Fan-you, Rainer S F, Oates W A. Phase diagram calculation: Past, present and future [J]. Progress in Materials Science, 2004, 49: 313-345.
[8] Jacot A, Rappaz M. A pseudo-front tracking technique for the modeling of solidification microstructures in multi-component alloys [J]. Acta Materialia, 2002, 50(8): 1909-1926.
[9] Geiger G H, Poirier D R. Transport phenomena in metallurgy [M]. New York: Addison-Wesley Publishing Company, 1973: 297-304.
[10] Welty J R, Wicks C E, Wilson R E, Rorrer G. Fundamentals of momentum, heat, and mass transfer [M]. New York: John Wiley & Sons, Inc, 2001: 205-270.
[11] XU Da-ming, BAI Yun-feng, FU Heng-zhi, GUO Jing-jie. Heat, mass and momentum transport behaviors in directionally solidifying blade-like castings in different electromagnetic fields described using a continuum model [J]. International Journal of Heat and Mass Transfer, 2005, 48: 2219-2232.
[12] XU Da-ming, GUO Jing-jie, FU Heng-zhi, SU Yan-qing, LI Qing-chun. Numerical solution to T-fS-CL coupling in binary dendrite solidification with any solid-back diffusion effects [J]. Transactions of Nonferrous Metals Society of China, 2003, 13(5): 1149-115.
[13] ThermoCalc Software A B. ThermoCalc Software User’ Guide (Version R) [M]. Stockholm: Stockholm Technology Park, 2006: 1-452.
[14] Vijayaraghavan R, Palle N, Boilean J, Zindel J, Beals R, Bradley F. A micro-model for aluminum-silicon a alloys [J]. Scripta Materialia, 1996, 35(7): 861-867.
[15] Gandin C A, Mosbah S, Volkmann T, Herlach D M. Experimental and numerical modeling of equiaxed solidification in metallic alloys [J]. Acta Materialia, 2008, 56(13): 3023-3035.
[16] Dong H B, Shin M M, Kurum, E C, Cama H, Hunt J D. A study of microsegregation in Al-Cu using a novel single-pan scanning calorimeter [J]. Metallurgical and Materials Transactions A 2003, 34(3): 441-447.
[17] Tenekedjiev N, Gruzleski J E. Thermal analysis of strontium treated hypoeutectic and eutectic aluminum-silicon casting alloys [J]. AFS Transactions, 1991, 35(99): 1-6.
[18] Roósz A. Exner H E, Numerical modeling of dendritic solidification in aluminum-rich Al-Cu-Mg alloys[J]. Acta Metall Mater, 1990, 38(2): 375-380.
[19] XU Da-ming. A unified micro-scale parameter approach to solidification-transport phenomena-based macrosegregation modeling for dendritic solidification: part I. Mixture average based analysis [J]. Metallurgical and Materials Transactions B, 2001, 32(6): 1129-1141.
[20] XU Da-ming. A unified micro-scale parameter approach to solidification-transport process-based macrosegregation modeling for dendritic solidification: part II. Numerical example computations [J]. Metallurgical and Materials Transactions B, 2002, 33(3): 451-463.
[21] BAI Yun-feng, XU Da-ming, GUO Jing-jieh, FU Heng-zhi, Numerical calculation for latent heat release in alloy casting of any solidification range using an extended temperature-compensation method [J]. Acta Metallurgical Sinica, 2003, 30(6): 623-629.
[22] Spinelli J E, Ferreira I L, Garcia A. Evaluation of heat transfer coefficients during upward and downward transient directional solidification of Al-Si alloys [J]. Struct Multidisc Optim, 2006, 31(3): 241-248.
[23] Sun H C, Chao L S. Analysis of interfacial heat transfer coefficient of green sand mold casting for aluminum and Tin-Lead alloys by using a lump capacitance method [J]. Journal of Heat Transfer, 2007, 129(4): 595-600.
[24] BU Kun, LI Yong-yi, DONG Yi-wei, JIANG Rui-song, TIAN Kun. Determination of interfacial heat transfer coefficient during single crystal blade casting process [J]. Foundry, 2009, 58(3): 225-228. (in Chinese)
基于Thermo-Calc及T-fS-CL耦合方法预测Biot0.1的合金凝固路径
赵光伟1，李新中1，徐达鸣1，郭景杰1，傅恒志1，杜 勇2，贺跃辉2
1. 哈尔滨工业大学 材料科学与工程学院，哈尔滨 150001；
2. 中南大学 粉末冶金国家重点实验室，长沙 410083
摘 要：将二元合金枝晶凝固传输模型及相应的T-fS-CL耦合求解方法扩展到描述多元合金在Biot?0.1条件下的凝固。基于提出的扩展模型及算法，提出一种考虑传热影响的预测Biot?0.1合金凝固路径及微观偏析的方法。该算法与Thermo-Calc热力学计算软件接口程序TQ6相耦合，用于实时计算每次迭代需要的热力学数据。Al-2Si-3Mg三元合金实例计算证实提出的模型及算法和凝固路径与微观偏析预测方法的实用性与可靠性，Al-5.17Cu-2.63Si三元合金凝固实验结果与预测结果的取得较好的一致性。
关键词：Thermo-Calc；凝固传输；凝固路径；微观偏析
(Edited by FANG Jing-hua)
Foundation item: Projects (2008112042) supported by the Open Project of State Key Laboratory of Powder Metallurgy of Central South University, China; Projects (50771041, 50801019) supported by the National Natural Science Foundation of China; Project (2011CB610406) supported by the National Basic Research Program of China
Corresponding author: ZHAO Guang-wei; Tel: +86-451-86418815; E-mail: zgwhit@163.com; damingxu@hit.edu.cn
DOI: 10.1016/S1003-6326(11)61153-9
Abstract: A binary continuum model for dendritic solidification transport phenomena and corresponding numerical algorithm for the strong nonlinear coupling of T-fS-CL were extended to multicomponent alloys solidified under condition of Biot?0.1. Based on the extended model/algorithm, a method considering heat transfer was proposed to predict the solidification paths and microsegregation of alloys solidified under the same condition. The new algorithm and method were closely coupled with the commercial Thermo-Calc package via its TQ6-interface codes for instantaneous determination of the related thermodynamic data at each calculation time step. The sample simulation performed on an Al-2Si-3Mg alloy system indicates the availability and reliability of the model/algorithm and the proposed method for predicting solidification paths and microsegregation. Computional and experimental investigations on an Al-5.17Cu-2.63Si ternary alloy were conducted, and a reasonable agreement between the computation and experiment was obtained.
