Trans. Nonferrous Met. Soc. China 23(2013) 2408-2415
Application of molecular interaction volume model in separation of Pb-Sn-Sb ternary alloy by vacuum distillation
Ling-xin KONG1,2,3, Bin YANG1,2,3, Bao-qiang XU1,2,3, Yi-fu LI1,2, Liang LI1,2, Da-chun LIU1,2, Yong-nian DAI1
1. National Engineering Laboratory for Vacuum Metallurgy, Kunming University of Science and Technology, Kunming 650093, China;
2. State Key Laboratory Breeding Base of Complex Nonferrous Metal Resources Clear Utilization in Yunnan Province, Kunming 650093, China;
3. Key Laboratory for Nonferrous Vacuum Metallurgy of Yunnan Province, Kunming 650093, China
Received 4 July 2012; accepted 30 October 2012
Abstract:
Based on the molecular interaction volume model (MIVM), the activities of components of Pb-Sn-Sb ternary alloy were predicted. The vapor-liquid phase equilibrium of Pb-Sn-Sb alloy system was calculated using the activity coefficients of Pb-Sn-Sb alloy system in the process of vacuum distillation. The calculated results show that the content of Sn in vapor phase increases with the increasing distillation temperature and content of Sn in liquid phase. However, the content of Sn in vapor phase is only 0.45% (mass fraction) while 97% in liquid phase at 1100 °C, which shows that the separating effect is very well. Experimental investigations on the separation of Pb-Sn-Sb ternary alloy were carried out in the distillation temperature range of 1100-1300 °C under vacuum condition. It is found that the Sn content in vapor phase is 0.54% while 97% in liquid phase at 1100 °C. Finally, the predicted data were compared with the experimental results showing good agreement with each other.
Key words:
molecular interaction volume model; vacuum distillation; Pb-Sn-Sb alloy; phase equilibrium;
1 Introduction
The raw materials which were used to produce Sn usually contain Pb and Sb. It is necessary to find an economic and convenient method to separate these metals. The processes which were used widely in the past, whether the chemical process (e.g., chloridization, oxidization, etc) or the electrolysis, is not consummate because of the long flow sheet, lower recovery of metals, need for retreating the by-products, and evident environmental pollution etc [1,2].
Vacuum distillation is regarded as one of the most effective and environment-friendly methods for metal separation and purification [3], which has been successfully used for the separation of Pb-Ag, Pb-Sn [4] and many other alloys, e.g. Sn-Sb, Pb-Sb, Pb-Ag, etc. [5] and the preparation of many high-purity metals, such as In and Te. It is more viable than time consuming crystallization, in terms of higher purification range and yield reached in less time in vacuum distillation [6]. Besides, it has many advantages, such as high recovery of metals (more than 99%), simple flow sheet, low power consumption and simple equipment. At the same time, a good separating effect has been achieved. However, the investigation about the separation of ternary alloys by vacuum distillation is limited.
The knowledge of the thermodynamic properties of alloys is important for providing important thermodynamic information in metallurgical process. A great deal of binary data were available in handbooks, such as Ref. [7]. But multi-component data are quite scarce because the experimental thermodynamic study is difficult and very time-consuming. Therefore, theoretical predicting is a significant and effective approach to obtain thermodynamic properties of multi-component alloys. The molecular interaction volume model (MIVM) proposed by TAO [8] has been successfully used in predicting thermodynamic properties of binary and multi-component alloys and the predicting effect is very well [9-12].
In this study, the activity of Pb-Sn-Sb ternary alloy system was predicted based on the MIVM. The vapor-liquid phase equilibrium was then calculated using the activity coefficients in the process of vacuum distillation. Experiments for the separation of Pb-Sn-Sb alloy were carried out for the proper interpretation of the results of the MIVM, and a comparison between the predicted data of MIVM and the experimental results was also executed.
2 Method
2.1 Vapor pressure
The fundamental condition to determine whether Pb-Sn-Sb ternary alloy can be separated by vacuum distillation is the difference of the vapor pressure of Pb, Sn and Sb in pure state. The saturated vapor pressure of pure substances can be calculated from the Van Laar Equation expressed as [13]
(1)
where p* is the saturated vapor pressure of pure substances; A, B, C and D are the evaporation constants given in Table 1 for the components Pb, Sn and Sb [14]; and T is the absolute temperature.
Table 1 Evaporation constants of Van Laar Equation for components Pb, Sn and Sb [14]
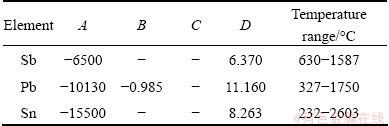
Using the data given in Table 1, the saturated vapor pressure of pure components Pb, Sn and Sb dependence of temperature can be drawn, which is shown in Fig. 1. A comparison of their values at the same temperature can be used as a rough guide in determining those elements which should exhibit preferential evaporation. As a first approximation, one dissolved element with a higher vapor pressure can be expected to evaporate preferentially. Others with lower vapor pressure can be concentrated in residual after vacuum distillation.
As can be seen from Fig. 1 that the saturated vapor pressure of Sn is the smallest among these three components, and that of Sb is the largest. Both the saturated vapor pressures of Pb and Sb are larger than that of Sn, which means that Pb and Sb will evaporate preferentially into vapor phase while Sn is still staying in liquid phase.
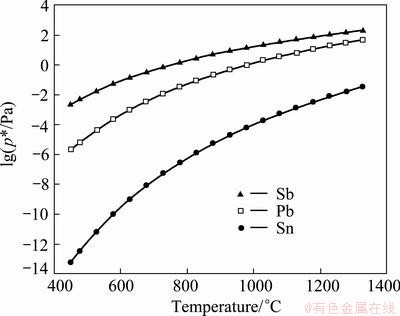
Fig. 1 lg p* at different temperatures
2.2 Separation coefficient
In order to further demonstrate the feasibility and the separating degree of different elements in Pb-Sn-Sb alloy during vacuum distillation, DAI and YANG [14] conducted the separation coefficient, β, which can be used to determine whether two elements can be separated from each other by vacuum distillation according to thermodynamic equilibrium theory. The separation coefficient was presented as follows:
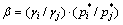(2)
where γi and γj are the activity coefficient of i and j components, respectively; 
and 
are the saturated vapor pressures of i and j in pure state, respectively. If the value of β is known, the ratio of actual vapor pressures of i and j can be expressed as
(3)
where pi and pj are the actual vapor pressures of components i and j, xi and xj are the molar concentrations of components i and j, respectively.
When β>1 or β<1, the separation of alloys could happen, but when β=1 it could not. Therefore, the separation coefficient β can be used to predict whether the components may be separated by vacuum distillation for all alloys.
2.3 Vapor-liquid phase equilibrium
In order to quantitatively predict the element distribution of Pb-Sn-Sb alloy, the vapor-liquid phase equilibrium of the Pb-Sn-Sb alloy was investigated. When the two phases are equilibrium, the mass fraction, wi,g, in gas phase is related to the vapor densities of these three components as
(4)
where ρi, ρj and ρk are the vapor densities for vapor component i, j and k, respectively, and ρj /ρi =wj,l /βwi,l, ρk /ρi=wk,l /βwi,l. Then the mass fraction of component i in vapor phase can be expressed as [14]
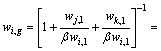
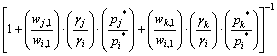(5)
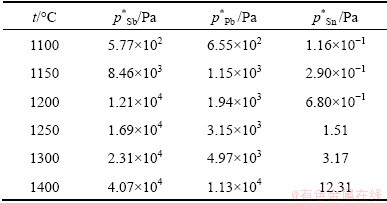
The relationship diagram of wi,g—ωi,l can be calculated by γ, p* and a series of wj,l/wi,l, wk,l/wi,l at specific temperatures, that is the vapor–liquid equilibrium composition for i–j–k system. The vapor pressures of pure Pb, Sn and Sb at different temperatures are shown in Table 2.
Table 2 Vapor pressure of components at different temperatures
2.4 Molecular interaction volume model
The MIVM was obtained from the physical prospect of liquid molecular movements in that liquid molecules are not like gas molecules, which are in continuous irregular motion, and not like solid ones, which are vibrating continuously at one site but are migrating non-randomly from one cell to another. This means that the basic feature of moving of liquid molecules is nonrandom migrating, and more details are in Ref. [9]. It is a two-parameter model and is able to predict the thermodynamic properties in a multi-component solution system using only the ordinary physical quantities of pure liquid metals and the related binary infinite dilute activity coefficients. The prediction effect of MIVM is of better stability and safety in previous work [11,12]. According to MIVM, the molar excess Gibbs energy 
of the liquid mixture i-j can be expressed as
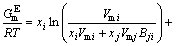
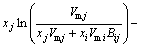
(6)
The expressions of activity coefficients of the components i and j can be respectively expressed as
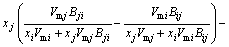
(7)
(8)
Extending Eq. (6) to a multi-component mixture, its molar excess Gibbs energy can be expressed as
(9)
And the expression of activity coefficient of any component i is
(10)
where Zi is the nearest molecule or first coordination number; xi, xj and xk are the molar fractions of component i, j and k, respectively; and the pair-potential energy interaction parameters Bij and Bji are defined as
(11)
where εii, εjj and εij are the i–i, j–j, and i–j pair-potential energies, εij = εji, k is the Boltzmann constant.
In order to determine the required binary parameters Bij and Bji, the infinite dilution activity coefficients of the binary liquid alloys and the related parameters of their components must be obtained. The related parameters of pure metals were available in Refs. [15,16]. The coordination number Zi of liquid metals can be predicted from their atomic parameters, molar volumes, melting points and melting enthalpies. The infinite dilution activity coefficients of binary liquid alloys [7] and the required binary parameters Bij and Bji are shown in Table 3.
Table 3 Values of 
, 
, Bij and Bji of related binary alloys i-j at required temperatures
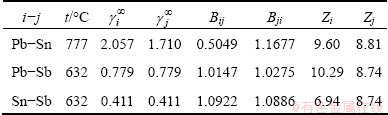
For a binary system i-j, the expression of infinite dilute activity coefficients 
and 
can be written from Eq. (8) when xi or xj approaches zero, respectively:
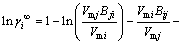
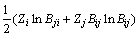(12)
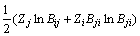(13)
Therefore, the values of Bij and Bji can be calculated from Eqs. (12) and (13) by the Newton–Raphson methodology.
Let us assume that the pair-potential energy parameters in Eq. (11), -(εji-εii)/k and -(εij-εjj)/k, are independent of temperature. Thus, we can get the values of Bji and Bij at other temperature from Eq. (11) if the values of Bji and Bij at given temperature are known.
Let the Pb-Sn-Sb liquid alloy be the 1-2-3 system, the activity coefficient of the component 1 of the system can be written from Eq. (10) as
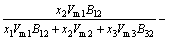
(14)
3 Experimental
3.1 Material
The material was provided by a tin smelting company of China, and the chemical composition of the material is listed in Table 4.
Table 4 Chemical composition of material (mass fraction, %)
3.2 Equipments and procedure
The laboratory apparatus for separation (see Fig. 2) mainly consisted of vacuum resistance furnace, vacuum pump, circulating water control system, graphite evaporator and condenser.
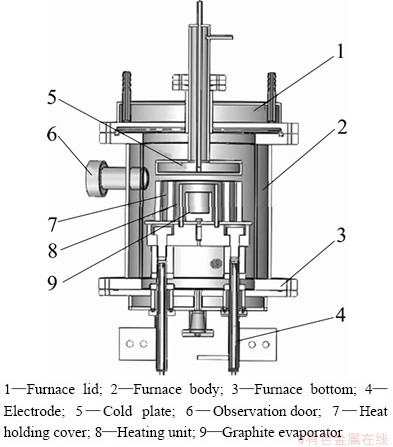
Fig. 2 Internal structure schematic diagram of vacuum furnace
The separation of Pb-Sn-Sb ternary alloy was carried out in a clean room of vacuum furnace. In a typical run of the distillation, raw Pb-Sn-Sb ternary alloy weighing 180 g was taken into the graphite crucible and placed inside the distillation section of the furnace, which was then evacuated to a vacuum of 10 Pa by means of a two-stage pumping system consisting of a mechanism pump and a blower. Melt temperatures during investigation were in the range of 1100-1300 °C, and the soaking (distillation) time was 30 min. Pressure was measured using a stand McLeod Gauge which was accurate to within 1% at pressures below 300 Pa. The feeding material was heated to different distillation temperatures at a heating rate of 50 °C/min and the temperatures were kept for 30 min when the chamber pressure was 10 Pa. The distillation temperature accuracy could be maintained at a constant value of better than 10 °C. Melt temperatures in all experiments were controlled by manually adjusting the furnace power input on the basis of continuous readings from mullite sheath- protected thermocouples inserted into molten alloy bath.
After completion of the distillation process, the temperatures in the evaporating distillation zone as well as condensing zone were lowered to room temperatures to solidify respectively the purified residue Sn and the condensed Pb and Sb.
Finally, the samples were collected from the volatile and residue phases and then mixed respectively to obtain the average concentration of samples. Flame atomic absorption spectroscopy (FAAS) and chemical analysis methods were used to determine the contents of Pb, Sn and Sb in both the volatile and residue.
4 Results and discussion
Substituting the corresponding Bji and Bij into Eq. (14), the activity of components of the liquid Pb-Sn-Sb alloy was predicted, as shown in Fig. 3.
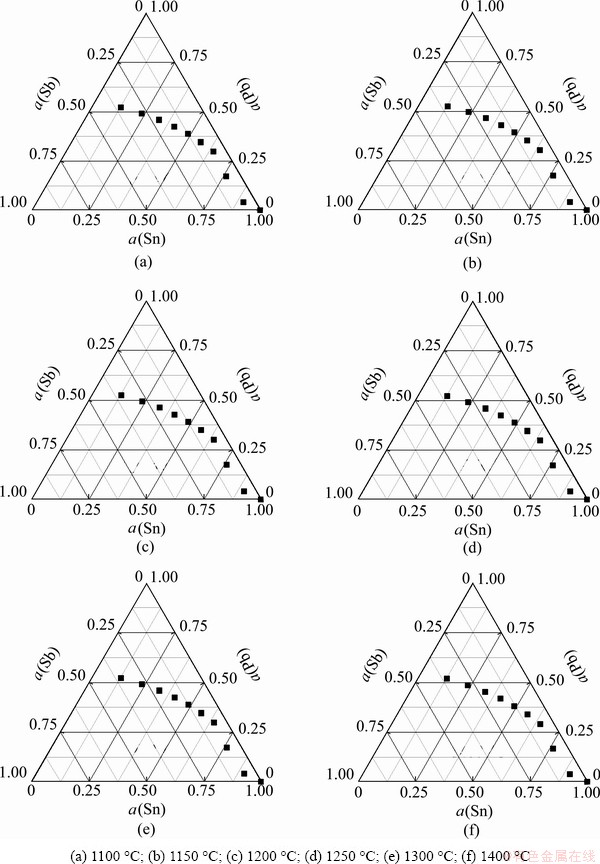
Fig. 3 Predicted activities (a) of components of Pb-Sn-Sb alloy with x(Sn)=0.1-1.0 (interval=0.1), x(Pb)= 0-0.45 (interval=0.05) and x(Sb)=0-0.45 (interval=0.05)
Substituting the activity coefficients γPb, γSn, γSb, saturated vapor pressures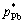 
, 
, 
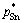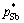and a series of wPb,l/wSn,l, wSb,l/wSn,l into Eq. (5) , the vapor–liquid phase equilibrium of Pb-Sn-Sb alloy system can be easily calculated at the required temperatures, as shown in Fig. 4.
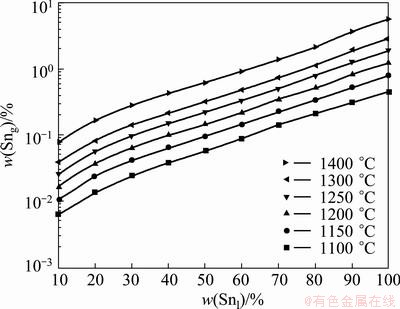
Fig. 4 Vapor–liquid equilibrium composition of Pb-Sn-Sb system at different temperatures
Figure 4 shows the change of equilibrium composition of vapor and liquid phase at different temperatures. It can be seen from Fig. 4 that the content of Sn in vapor phase increases with the increasing distillation temperature and content of Sn in liquid phase. However, the content of Sn in vapor phase is 0.45% while 97% in liquid phase at 1100 °C. This means that Sn can be separated from Pb and Sb by vacuum distillation thoroughly.
Tables 5 and 6 summarize the experimental conditions, feeding amount, and mass ratio of the volatile and residue phases of each experiment, as well as the content of components of Pb-Sn-Sb in volatile and residue phases, respectively.
As can be seen from Table 5 that the yield of the volatile increases with the increasing distillation temperature. This is because the amount of evaporated Pb and Sb increases, and the higher the distillation temperature, the well the separating effect. But the loss of the material increases with the increasing distillation temperature. The reason is that the volatile cannot condense on the condenser plate completely. Some of the volatile condense onto the inner wall or dead area of the vacuum furnace and cannot be collected.
It can be seen from Table 6 that the content of Sn in vapor phase increases with the increasing distillation temperature, this behavior can be anticipated that increasing temperature causes an increase in saturated vapor pressure of Sn. The temperature dependence of the content of Sn in vapor phase, was determined in the temperature range of 1100-1300 °C while the content of Sn in liquid phase is 97 %, and the data are plotted in Fig. 5.
It can be seen from Fig. 5 that the content of Sn in vapor phase increases with the increasing distillation temperature while the content of Sn in liquid phase is 97%. The content of Sn in vapor phase, however, is only 0.54% at 1100 °C, which indicates that Pb and Sb evaporate into vapor phase while Sn is still staying in liquid phase. Thus, Sn can be separated from Pb and Sb by vacuum distillation thoroughly. The results are consistent with the predicted results. In order to further verify the efficiency of the predicted results, the experimental results and the predicted data were compared directly in Fig. 6.
Table 5 Experimental conditions and results
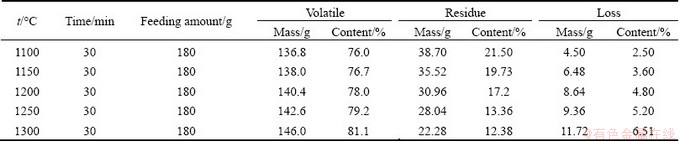
Table 6 Experimental results
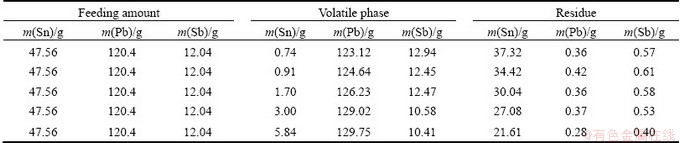
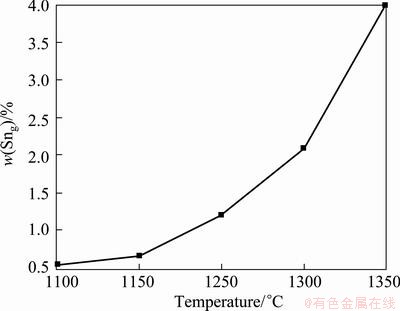
Fig. 5 Content of Sn in vapor phase dependence of distillation temperature
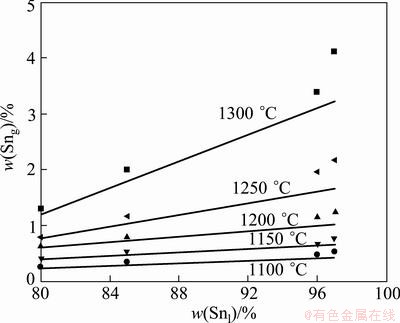
Fig. 6 Comparison of predicted content of Sn in vapor phase of MIVM (lines) with experimental data (symbols) at 1100- 1300 °C
As can be seen from Fig. 6 that the content of Sn in vapor phase increases with the increasing distillation temperature and content of Sn in liquid phase. This behavior can be anticipated that the increasing distillation temperature results in an increase in saturated vapor pressure of Sn, thus, the volatile quantity of Sn increases correspondingly. It can also be seen from Fig. 6 that the predicted data are in good agreement with the experimental results, although a little deviation was observed, and the higher the temperature, the greater the deviation. The reasons may arise from the accuracy of the experimental technique and the thermodynamic data, and the MIVM, especially for asymmetry systems [17]. The condensate Pb and Sb can also be separated by vacuum distillation which was investigated in Ref. [6].
5 Conclusions
1) Based on the MIVM, the activity of Pb-Sn-Sb ternary alloy system was predicted.
2) The vapor-liquid phase equilibrium of Pb-Sn- Sb alloy system in vacuum distillation was predicted using the activity coefficients. The predicted results show that the content of Sn in vapor phase increases with the increasing distillation temperature and content of Sn in liquid phase. The ratio of content of Sn in liquid phase to that in vapor phase is up to hundreds, and the content of Sn in vapor phase is 0.45% while 97% in liquid phase at 1100 °C.
3) Experiments for separation of Pb-Sn-Sb alloy were executed in the temperature range of 1100-1300 °C. The results show that the content of Sn in vapor phase increases with the increasing distillation temperature and content of Sn in liquid phase. The content of Sn in vapor phase is 0.54 % while 97% in liquid phase at 1100 °C.
4) The experimental results are in good agreement with the predicated values, although a little deviation was observed. This error may be due to the accuracy of the experimental technique and condition as well as the MIVM, and may also arise from out of consideration of the changes in constituent, activity and distribution coefficient of component in vacuum distillation process were not considered. The present study is helpful to get more reliable results in vacuum distillation because MIVM has a good physical basis and provides a rigorous model on which to base refining simulations for ternary alloys.
References
[1] DAI Yong-nian. Vacuum distillation and separation of Pb-Sn alloy [J]. Nonferrous Metals, 1977(9): 24-30. (in Chinese)
[2] DAI Yong-nian. HE Ai-ping. Vacuum distillation of lead-tin alloy [J]. Journal of Kunming Institute of Technology, 1989, 14(3): 16-27.
[3] QIU Ke-qiang, WU Qian, ZHAN Zhi-hua. Vacuum pyrolysis characteristics of waste printed circuit boards epoxy resin and analysis of liquid products [J]. Journal of Central South University: Science and Technology, 2009, 40(5): 1209-1215. (in Chinese)
[4] YANG Hong-wei, XU Bao-qiang, YANG Bin, MA Wen-hui, TAO Dong-ping. Calculation of phase equilibrium in vacuum distillation by molecular interaction volume model [J]. Fluid Phase Equilibria, 2011, 3: 78-81.
[5] YANG Hong-wei, YANG Bin, XU Bao-qiang, LIU Da-chun, TAO Dong-ping. Application of molecular interaction volume model in vacuum distillation of Pb-based alloys [J]. Vacuum, 2012, 86(9): 1296-1299.
[6] ALI S T, SRINIVAS RAO, LAXMAN C, MUNIRATHNAM N R, PRAKASH T L. Preparation of high pure zinc for electronic applications using selective evaporation under vacuum [J]. Separation and Purification Technology, 2012, 85: 178-182.
[7] HULTGREN R, DESAI P D, HAWKINS D T, GEISER M, KELLEY K K. Selected values of the thermodynamic properties of binary alloys [M]. American Society of Metals, Metals Park, OH, 1973.
[8] TAO Dong-ping. A new model of thermodynamics of liquid mixtures and its application to liquid alloys [J]. Thermochimica Acta, 2000, 363: 105-113.
[9] TAO Dong-ping, YANG Bin, LI Deng-fang. Prediction of the thermodynamic properties of quinary liquid alloys by modified coordination equation [J]. Fluid Phase Equilibria, 2002, 193: 167-177.
[10] TAO Dong-ping. A comparison of the molecular interaction volume model with the subregular solution model in multicomponent liquid alloys [J]. Metallurgical and Materials Transactions A, 2004, 35(2): 419-424.
[11] TAO Dong-ping. Prediction of the coordination numbers of liquid metals [J]. Metallurgical and Materials Transactions A, 2005, 36: 3495-3497.
[12] TAO Dong-ping. Molecular entity vacancy model [J]. Fluid Phase Equilibria, 2006, 250: 83-92.
[13] ZHENG Song-sheng, CHEN Wen-hui, CAI Jing, LI Jin-tang, CHEN Chao, LUOXue-tao. Mass transfer of phosphorus in silicon melts under vacuuminduction refining [J]. Metallurgical and Materials Transactions B, 2010, 41:1268-73.
[14] DAI Yong-nian, YANG Bin. Vacuum metallurgy for non-ferrous metals and materials [M]. Beijing: Metallurgical Industry Press, 2000. (in Chinese)
[15] LIDA T, GUTHRIE R I L. The physical properties of liquid metals [M]. Oxford: Clarendon Press, 1988.
[16] FERRO R, SACCONE A. Structure of solids [M]. Weinheim: VCH Verlagasgesellschaft, 1993.
[17] ZAHNG Zheng-he, SU Yan-qing, CHEN Da-zhou, GUO Jing-jie, FU Heng-zhi. Dynamics model for evaporation loss calculation of alloying elements [J]. Foundry, 2009, 58(4): 373-375.
分子相互作用体积模型在真空蒸馏分离铅-锡-锑三元合金中的应用
孔令鑫1,2,3，杨 斌1,2,3，徐宝强1,2,3，李一夫1,2，李 亮1,2，刘大春1,2，戴永年1
1. 昆明理工大学 真空冶金国家工程实验室，昆明 650093；
2. 云南省复杂有色金属资源清洁利用国家重点实验室(培育基地)，昆明 650093；
3. 云南省有色金属真空冶金重点实验室，昆明 650093
摘 要：基于分子相互作用体积模型(MIVM)，计算Pb-Sn-Sb三元合金体系的活度，并使用活度系数计算真空蒸馏过程中Pb-Sn-Sb三元合金体系的气液相平衡。结果表明：随着蒸馏温度和液相中锡含量的增加，气相中锡含量也不断增加；然而，在1100 °C液相中锡含量为97%(质量分数)时，气相中锡含量仅为0.45%，分离效果较好。在真空(10 Pa)条件下，在1100~1300 °C蒸馏温度范围内进行真空蒸馏分离Pb-Sn-Sb三元合金实验。结果表明：在1100 °C时，当液相中锡含量为97%时，气相中锡含量为0.54%。最后对比分析了实验结果和预测值，分析表明实验结果和预测值吻合较好。
关键词：分子相互作用体积模型；真空蒸馏；铅-锡-锑合金；相平衡
(Edited by Xiang-qun LI)
Foundation item: Project (2012CB722803) supported by the National Basic Research Program of China; Project (2011FA008) supported by the Key Project of Science and Technology Program of Yunnan Province, China
Corresponding author: Bin YANG; Tel: +86-871-5163583; E-mail: kgyb2005@126.com; kkmust@126.com
DOI: 10.1016/S1003-6326(13)62748-X
Abstract: Based on the molecular interaction volume model (MIVM), the activities of components of Pb-Sn-Sb ternary alloy were predicted. The vapor-liquid phase equilibrium of Pb-Sn-Sb alloy system was calculated using the activity coefficients of Pb-Sn-Sb alloy system in the process of vacuum distillation. The calculated results show that the content of Sn in vapor phase increases with the increasing distillation temperature and content of Sn in liquid phase. However, the content of Sn in vapor phase is only 0.45% (mass fraction) while 97% in liquid phase at 1100 °C, which shows that the separating effect is very well. Experimental investigations on the separation of Pb-Sn-Sb ternary alloy were carried out in the distillation temperature range of 1100-1300 °C under vacuum condition. It is found that the Sn content in vapor phase is 0.54% while 97% in liquid phase at 1100 °C. Finally, the predicted data were compared with the experimental results showing good agreement with each other.
