- Abstract:
- 1 Introduction▲
- 2 Analytical solutions of...▲
- 3 Verification of accurac...▲
- 4 Conclusions▲
- References
- Figure
- Fig.1 Crack along gradation direction in FGM medium and reference coordinate
- Fig.2 FGM medium with linear variation of elastic modulus
- Fig.3 Beam sample of FGMs with linear gradation loaded in four-point bending
- Fig.4 Finite element model for numerical experiment
- Fig.5 Local collocation estimates of stress intensity factor from finite element results
J. Cent. South Univ. Technol. (2010) 17: 1177-1184
DOI: 10.1007/s11771-010-0615-0![]()
Crack tip higher order stress fields for functionally graded materials with generalized form of gradation
YAN Xiu-fa(燕秀发)1, 2, QIAN Qi-hu(钱七虎)1, LU Hong-biao(卢红标)1,
WANG Wei(王玮)2, SUN Ao(孙翱)2
1. Engineering Institute of Engineering Corps, People’s Liberation Army University of Science and Technology,
Nanjing 210007, China;
2. People’s Liberation Army 91550 Unit, Dalian 116023, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract:
A generalized form of material gradation applicable to a more broad range of functionally graded materials (FGMs) was presented. With the material model, analytical expressions of crack tip higher order stress fields in a series form for opening mode and shear mode cracks under quasi-static loading were developed through the approach of asymptotic analysis. Then, a numerical experiment was conducted to verify the accuracy of the developed expressions for representing crack tip stress fields and their validity in full field data analysis by using them to extract the stress intensity factors from the results of a finite element analysis by local collocation and then comparing the estimations with the existing solution. The expressions show that nonhomogeneity parameters are embedded in the angular functions associated with higher terms in a recursive manner and at least the first three terms in the expansions must be considered to explicitly account for material nonhomogeneity effects on crack tip stress fields in the case of FGMs. The numerical experiment further confirms that the addition of the nonhomogeneity specific terms in the expressions not only improves estimates of stress intensity factor, but also gives consistent estimates as the distance away from the crack tip increases. Hence, the analytical expressions are suitable for the representation of crack tip stress fields and the analysis of full field data.
Key words:
1 Introduction
Recent advances in materials processing and engineering have led to a new class of materials called functionally graded materials (FGMs) that possess spatially varying composition and mechanical properties. FGMs are unique in that they offer the possibility of tailoring their constituents and gradation to match the end use [1]. Therefore, they are currently considered for many demanding engineering applications including military armor, earth moving equipment, thermal barrier coatings for turbine blades and internal combustion engines, machine tools and so on. Even though the initial research on FGMs is largely motivated by the practical applications of the concept in a wide variety of thermal shielding problems, materials with graded physical properties have almost unlimited potential in many other technological applications.
Experimental results show that fracture remains a key failure mode of these materials [2]. Consequently, FGMs pose new challenges in terms of modeling, characterization and optimization from the point of view of fracture behavior [3]. So far, considerable researches on various aspects of fracture in the FGM have been carried out. In the early work, EISCHEN [4], using a series representation of variation of elastic modulus, showed that the leading term in the crack tip stress field was of the inverse square root form for any functional form of elastic modulus variation. SHUKLA et al [5] reviewed the elementary concepts of fracture mechanics of FGMs and then presented a comprehensive experimental study of dynamic crack growth using the optical method of reflection photoelasticity and high-speed photography. Assuming that the shear modulus varied exponentially, the behavior of two parallel cracks in FGMs subjected to a tensile stress loading was investigated using Schmidt method by LIANG [6] and it was also revealed that the crack shielding effect was present in FGMs. MA et al [7] considered the plane strain problem of a crack in a functionally graded strip with a power form shear modulus by means of Fourier transform and obtained both mode I and mode II stress intensity factors (SIFs) at the crack tip of FGMs for a pure normal loading or a pure shear loading. CHEN and CHUE [8] studied antiplane fracture problems of two bonded functionally graded strips with internal cracks by using Gauss–Chebyshev integration formula for numerically solving a system of singular integral equations and further discussed the effects of material nonhomogeneous parameters, crack locations and boundary conditions on the stress intensity factor. Subsequently, CHEN et al [9] studied an antiplane collinear crack problem for a strip of FGMs with mixed boundary conditions by the similar method. The primary conclusions of the above investigations are that the classical inverse square root singular nature of the crack tip stress field is preserved in FGMs, but the stress intensity factor is influenced by material nonhomogeneity and the structure of the stress field away from crack tip is significantly altered. In addition, the SIFs for cracks in FGMs for different geometry and loading conditions are provided.
However, because of the mathematical difficulties arising from the fact that the properties of FGMs can vary arbitrarily in space, for the gradation form in a general sense, crack tip higher order stress fields in FGMs embodying nonhomogeneity specific terms for individual stress components have not been developed. Such stress fields are necessary in the analysis of full field experimental data obtained through techniques such as photoelasticity and coherent gradient and sensing (CGS) or computational results obtained by numerical methods. Most of stress fields currently available are obtained through integral transform method and the inversion has to be carried out numerically, making these stress field expressions not feasible for the extraction of fracture parameters from experimental data or numerical results [10-11]. PARAMESWARAN and SHUKLA [12] developed the structure of the first stress invariant and the out of plane displacement to bring out the effects of nonhomogeneity. However, nonhomogeneity specific terms for individual stress components were not derived. LEE [13] provided three-term asymptotic expansions of crack tip stress fields for a crack in an FGM. But, universal differential equations to solve arbitrary order expansions were not developed, and then characteristics of crack tip higher order stress fields for FGMs were not explicitly revealed. It is also important to point out that, owing to complexity of the problem, all the existing studies on crack tip stress fields have to be confined to exponential or linear variation of material properties. Moreover, so far, the validity of asymptotic expansions available for representing crack tip fields has not been investigated and verified.
In this work, to overcome the disadvantages of the works before-mentioned, a generalized form of material gradation applicable to a more broad range of FGMs was presented. The crack tip higher order stress fields for opening mode and shear mode cracks embodying nonhomogeneity specific terms for individual stress components under quasi-static loading were developed under the material model through the approach of asymptotic analysis. Not only were the six-term expansions of the stress fields obtained, but also universal differential equations for solving arbitrary term expansions were derived. On the basis of the analytical expressions, characteristics and structure of crack tip higher order stress fields for FGMs were completely revealed. In addition, in order to verify the accuracy of the higher order stress fields above-developed for representing crack tip stress fields and their validity in the full field data analysis, a numerical experiment was conducted by using them to extract the stress intensity factor from full field data obtained from a finite element analysis.
2 Analytical solutions of crack tip higher order stress fields for FGMs with generalized form of gradation
2.1 Theoretical formulation
The physical properties of FGMs varied from point to point in the material. At a given point in the material, the properties could be assumed to be the same in all directions, and hence at a continuum level FGMs were isotropic nonhomogeneous solids. For instance, large bulk FGMs produced by spark plasma sintering (SPS) technique might be modeled as isotropic materials. Therefore, a nonhomogeneous isotropic model might be appropriate in studying the mechanics of FGMs. In this work, crack tip higher order stress fields were investigated under the model.
The plane elasticity problem of a finite crack lying in a medium of FGMs was considered here. Without losing generality, it was assumed that the material properties, such as elastic modulus E and Poisson ratio μ, varied according to
![]() (1)
(1)
where E and μ are continuous, bounded and at least piecewise differentiable functions. The in-plane stress components (σij, i,j∈{x,y}) can be defined in terms of Airy’s stress function F=F(x, y), as given by
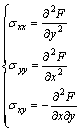 (2)
(2)
Substituting Eq.(2) into the compatibility equation through Hooke’s law, the compatibility equation for the plane problem can be expressed as
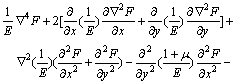
![]() (3)
(3)
where![]()
![]() Eq.(3) is
Eq.(3) is
for the generalized plane stress. The corresponding equation for plane strain is obtained by replacing E and μ by E/(1-μ2) and μ/(1-μ), respectively.
2.2 Generalized gradation form and governing equations
Consider the plane elasticity problem containing a finite crack with length of 2S on y=0 plane as shown in Fig.1. In the previous study [14], it was shown that the effect of Poisson ratio μ on crack tip stress fields was rather negligible. Consequently, μ might be assumed to be constant in the study of fracture mechanics of FGMs. In addition, the variation of the elastic and physical properties of FGMs is in general limited to a single direction. Hence, in order to describe more extensive variation of material property of FGMs, a generalized form of gradation is presented as follows:
![]() (4)
(4)
where E0 is the elastic modulus at the crack tip (x=y=0); and β and k are nonhomogeneity parameters.
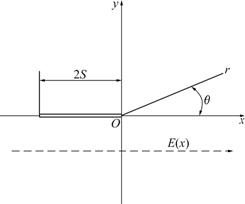
Fig.1 Crack along gradation direction in FGM medium and reference coordinate
Substituting Eq.(4) into Eq.(3), under the gradation model, the equation to be satisfied by the Airy’s stress function F=F(x, y) is
![]()
![]() (5)
(5)
For FGMs, the stress fields near the crack tip maintained the classical inverse square root singularity [4]. Therefore, expressing F(x, y) in terms of polar coordinates centered at the crack tip shown in Fig.1 as F(r, θ), it can be assumed that the stress function F(r, θ) can be expanded by a power series as follows:
![]() (6)
(6)
where![]() Switching Eq.(5) into polar
Switching Eq.(5) into polar
coordinates, the above series on substitution into Eq.(5) taking the form of polar coordinates leads to an infinite series involving differential equations associated with
each power of r (r-5/2, r-2, r-3/2, r-1, …, ![]() For Eq.(5)
For Eq.(5)
is valid for any arbitrary r, the differential equations corresponding to each power of r (r-5/2, r-2, r-3/2, r-1, …,
![]() should be identically zero. This leads to a set of
should be identically zero. This leads to a set of
differential equations for fn(θ) (n=1, 2, 3, …) as follows:
![]() (7)
(7)
![]() (8)
(8)
![]()
![]()
![]() (9)
(9)
![]()
![]()
![]() (10)
(10)
![]()
![]()
![]()
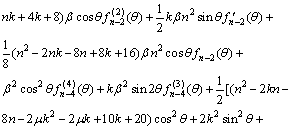

![]() (11)
(11)
In general, crack faces are supposed to be traction free, which correspond to the following boundary conditions:
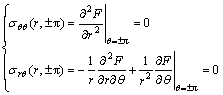 (12)
(12)
Substituting Eq.(6) into Eq.(12), Eq.(12) reduces to
![]() (13)
(13)
Solving the above-developed set of differential equations for fn(θ) (n=1, 2, 3,…) under boundary conditions (Eq.(13)), it should be noticed from Eqs.(9)- (11) that they are coupled to the lower order unknown functions such as f1(θ), f2(θ), fn-2(θ) and fn-4(θ), and Eqs.(7)-(8) can be solved easily. Hence fn(θ) (n≥3) can be obtained in a recursive manner. It is worth noting that Eqs.(11) and (13) are universal differential equations for solving arbitrary unknown functions fn(θ) (n≥5). The solutions of crack tip high order stress fields for opening mode and shear mode are provided in the following sections.
2.3 Crack tip higher order stress fields for opening mode loading
After obtaining F(r, θ), by substituting F(r, θ) for n≤6 into Eq.(2) taking the form of polar coordinates (r, θ), and considering the symmetry of the normal stress components about the line of the crack, a six-term expansion of the crack tip stress field for opening mode loading is obtained as follows:
![]()
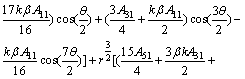

![]() (14)
(14)
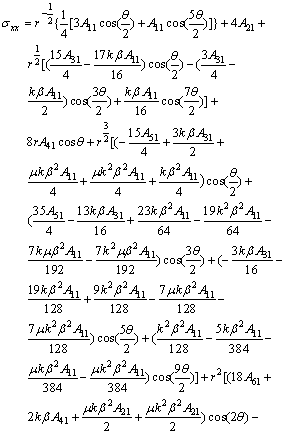
![]() (15)
(15)
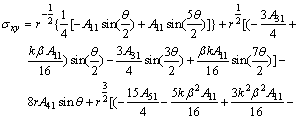 (16)
(16)
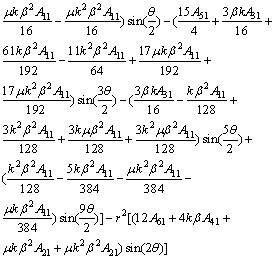
where A11, A21, A31, A41, A51 and A61 are unknown constants that can be determined by fitting the stress field to experimental or numerical data.
2.4 Crack tip higher order stress fields for shear mode loading
Following the same procedure and keeping in view the dissymmetry nature of the shear mode problem, the first six terms of the expansion for the stress field are obtained as

![]()
![]() (17)
(17)
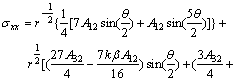 (18)
(18)

 (19)
(19)
where A12, A32, A42, A52 and A62 are unknown constants that can be determined by fitting the stress field to experimental or numerical data.
2.5 Characteristics of crack tip higher order stress fields for FGMs
It can be seen from the above-developed analytical expressions of crack tip higher order stress fields for FGMs, Eqs.(14)-(19), that they consist of two parts: the classical solution for homogenous materials and additional terms due to nonhomogeneity. By setting β or k to zero in the expressions, the stresses collapse to their homogeneous counterparts. However, unlike homogeneous materials, the stress fields contain terms having Poisson ratio for the presence of the Poisson ratio-dependent coefficient in the governing equation (Eq.(5)) as opposed to the bi-harmonic equation for homogeneous materials. The expressions further indicate that at least the first three terms in the expansions should be considered in the case of FGMs in order to explicitly account for nonhomogeneity effect on the structure of crack tip stress fields. However, the fourth term in the expansions is not affected by material nonhomogeneity. Thus, the first five terms of the expansions ought to be considered to further account for the effects of material nonhomogeneity on crack tip stress fields. Then, in order to entirely reveal the structure of crack tip higher order stress fields for FGMs, the six-term expansions above should be obtained. It can also be noted that the unknown coefficients of the angular functions associated with lower powers of r along with nonhomogeneity parameters, β and k, are embedded in the angular functions associated with higher powers of r in a recursive manner. Material nonhomogeneity shows that more evident influences on crack tip stress fields as power of r increases. A conclusion can be drawn that the angular functions corresponding to powers of r greater than 2 in the expansions all contain the terms whose coefficient includes nonhomogeneity parameters. In fact, the essential discrepancy between the crack tip higher order stress fields for FGMs presented here with ones of homogeneous materials is that the former will not satisfy the governing equations term-by-term, but only as a whole series in a more rigorous mathematical sense. Hence, the analytical expressions are of much more importance for representing the crack tip field for FGMs.
3 Verification of accuracy of crack tip higher order stress fields in representing crack tip stress fields and their validity in full field data analysis
3.1 Numerical example
Consider the beam sample of FGMs with the linear gradation form of elastic modulus for k=1 in Eq.(4) as shown in Fig.2, which is loaded in four-point bending under the plane stress condition as shown in Fig.3. In Figs.2-3, E=E(x), E1= E(0), E2= E(W), ?=C, a is the crack length, P is the loading, and W and L are the width and length of the beam, respectively.
Particular cases of sample and gradation form are chosen so that the results of the numerical experiment presented here can be compared with the existing solution [15]. The problem described above is a crack problem for opening mode loading. Then, the expansions
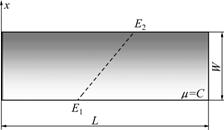
Fig.2 FGM medium with linear variation of elastic modulus
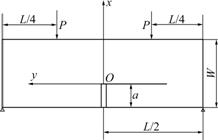
Fig.3 Beam sample of FGMs with linear gradation loaded in four-point bending
above-developed can be verified through Eq.(14). By setting k=1 in Eq.(14), stress![]() of crack tip fields for FGMs with the linear gradation of elastic modulus can be written as
of crack tip fields for FGMs with the linear gradation of elastic modulus can be written as
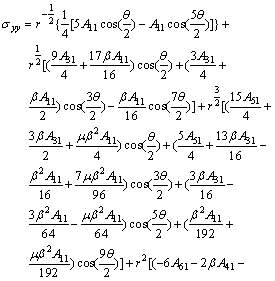
![]() (20)
(20)
By setting β to zero in the above equation, stress ![]() of crack tip fields for homogeneous materials can be obtained as
of crack tip fields for homogeneous materials can be obtained as

![]() (21)
(21)
The accuracy of the asymptotic expansions in representing crack tip stress fields is evaluated by using Eq.(20) to extract the stress intensity factors from the results of a finite element analysis by local collocation and comparing them with the known solution provided by ROUSSEAU and TIPPUR [15]. Their validity in full field data analysis is evaluated by comparing the stress intensity factors obtained by using Eq.(20) for FGMs with those obtained by using its homogeneous counterpart, Eq.(21).
3.2 Numerical implement and computational results
Numerical simulations of FGMs require implementing the required property variation, i.e., elastic modulus in the present case, in the problem domain. In the finite element analysis, this is done by discretizing the rectangular domain into rows of elements and imposing a constant value of elastic modulus to each row of elements. Then, a stepwise change in modulus is realized. For a mesh consisting of eight-node plane stress elements of size, a/200 is employed around the crack tip to model the edge crack (a/W=0.3, a/L=0.05) in the present numerical experiment, as shown in Fig.4. The level of nonhomogeneity is considered, which will result in the elastic modulus varying by a factor (E2 /E1) of 2.23 over a width of W. Due to the symmetry of the problem, only the right half of the specimen is considered in the analysis. The nodes in the region, -π≤θ≤0 and 0.1a≤ r≤a, are used as the local collocation points. Stress σyy at the each collocation node is calculated. Using σyy field, the coefficients of Eqs.(20)-(21) (A11, A21, …, A61) are obtained through an over deterministic least squares method, and then stress intensity factor KI can be obtained by the relation,![]()
Fig.5 shows the estimates of stress intensity factor KI extracted from the finite element stress σyy field. These estimates are obtained from the individual regions, Ri-1<r<Ri (Ri=0.1ai, i=2, 3, …, 10) around the crack tip, where Ri is the boundary of the data points, so that the accuracy and validity of crack tip higher order stress fields can be verified in different regions, respectively. The circles in Fig.5 indicate values of the stress intensity factor extracted using Eq.(20) for FGMs. It can be noticed that these values are closer to the results provided by ROUSSEAU and TIPPUR [15] than the estimates obtained by using Eq.(21) for homogeneous materials in all the regions of local collocation points. Moreover, these values are very consistent with the existing results as the distance away from the crack tip increases. On the contrary, the crosses in Fig.5, representing the estimates using Eq.(21), show that higher and higher errors are introduced as the distance away from the crack tip increases. It is not worthy to surprise that stress intensity factors obtained by both approaches in the regions very close to the crack tip are relatively coarse for numerical results of the standard finite element method are relatively inaccurate in the immediate vicinity of crack tip under the effect of singularity at the crack tip [16]. Contrarily, it is further confirmed that the addition of the nonhomogeneity specific terms in the above-developed crack tip higher order stress fields not only improves the estimates, but also gives consistent estimates of the stress intensity factor as the distance away from the crack tip increases. Hence, a conclusion can be drawn that the analytical expressions of crack tip higher order stress fields are suitable for the representation of crack tip stress fields and the analysis of full field data.
4 Conclusions
(1) Under a generalized form of material gradation applicable to a more broad range of FGMs, analytical expressions of crack tip higher order stress fields in a series form for opening mode and shear mode cracks are developed under quasi-static loading. It can be noted from the expressions that the unknown coefficients of the angular functions associated with lower order terms along with nonhomogeneity parameters are embedded in the angular functions associated with higher terms in a recursive manner. The essential characteristic of crack tip stress fields for FGMs is that the stress fields will not satisfy the governing equation term-by-term, but only as a whole series in a more rigorous mathematical sense.
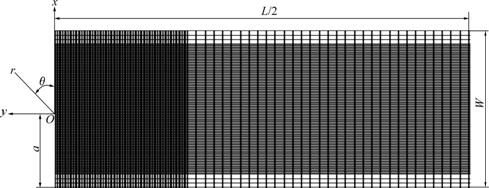
Fig.4 Finite element model for numerical experiment
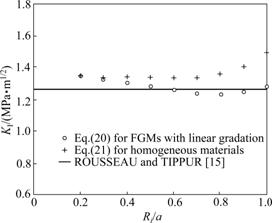
Fig.5 Local collocation estimates of stress intensity factor from finite element results
(2) A numerical experiment is conducted to verify the accuracy of the above-developed analytical expressions in representing crack tip stress fields and their validity for full field data analysis. It is confirmed that the addition of the nonhomogeneity specific terms in the crack tip higher order stress fields not only improves the estimates, but also gives consistent estimates of stress intensity factor as the distance away from the crack tip increases. Hence, the analytical expressions of crack tip higher order stress fields are suitable for the representation of crack tip stress fields and the analysis of full field data. They can further be the base of numerical methods for fracture analysis of FGMs such as the boundary collocation method and the higher order approximate method.
References
[1] DIAS C M, SAVASTANO H, JOHN V M. Exploring the potential of functionally graded materials concept for the development of fiber cement [J]. Construction and Building Materials, 2010, 24(2): 140-146.
[2] GUO L C, NODA N. Fracture mechanics analysis of functionally graded layered structures with a crack crossing the interface [J]. Mechanics of Materials, 2008, 40(1): 81-99.
[3] AHANKARI S S, KAR K K. Processing and characterization of functionally graded materials through mechanical properties and glass transition temperature [J]. Materials Letters, 2008, 62(32): 3398-3400.
[4] EISCHEN J W. Fracture of nonhomogeneous materials [J]. International Journal of Fracture, 1987, 34(1): 3-22.
[5] SHUKLA A, JAIN N, CHONA A. A review of dynamic fracture studies in functionally graded materials [J]. Stain, 2007, 43(2): 76-95.
[6] LIANG Jun. Basic solution of two parallel mode-I cracks in functionally graded materials [J]. Science in China Series E: Technological Sciences, 2008, 51(9): 1380-1393.
[7] MA Jin-ju, ZHONG Zheng, ZHANG Chuan-zeng. Analysis of a crack in a functionally graded strip with a power form shear modulus [J]. Acta Mechanica Solida Sinica, 2009, 22(5): 465-473.
[8] CHEN Y J, CHUE C H. Mode III crack problems of two bonded functionally graded strips with internal cracks [J]. International Journal of Solids and Structures, 2009, 46(3): 331-343.
[9] CHEN Y Z, LIN X Y, WANG Z X. Antiplane elasticity crack problem for a strip of functionally graded materials with mixed boundary condition [J]. Mechanics Research Communications, 2010, 37(1): 50-53.
[10] DING Sheng-hu, LI Xing. Anti-plane problem of periodic interface cracks in a functionally graded coating-substrate structure [J]. International Journal of Fracture, 2008, 153(1): 53-62.
[11] ZHONG Zheng, CHENG Zhan-qi. Fracture analysis of a functionally graded strip with arbitrary distributed material properties [J]. International Journal of Solids and Structures, 2008, 45(28): 3711-3725.
[12] PARAMESWARAN V, SHUKLA A. Asymptotic stress fields for stationary cracks along the gradient in functionally graded materials [J]. Journal of Applied Mechanics, 2002, 69(3): 240-243.
[13] LEE K H. Characteristics of a crack propagating along the gradient in functionally gradient materials [J]. International Journal of Solids and Structures, 2004, 41(21): 2879-2898.
[14] DELALE F, ERDOGAN F. The crack problem for a nonhomogeneous plane [J]. Journal of Applied Mechanics, 1983, 50(3): 609-614.
[15] ROUSSEAU C E, TIPPUR H V. Evaluation of crack tip fields and stress intensity factors in functionally graded elastic materials: Cracks parallel to elastic gradation [J]. International Journal of Fracture, 2002, 114(1): 87-111.
[16] HILTON P D, SIH G C. Applications of the finite element method to calculation of stress intensity factors [C] // Mechanics of Fracture. Leyden: Noordhoff International, 1973: 426-483.
Foundation item: Project(20080431344) supported by Postdoctoral Science Foundation of China; Project(51021001) supported by the National Natural Science Foundation of China
Received date: 2010-01-03; Accepted date: 2010-04-08
Corresponding author: YAN Xiu-fa, PhD; Tel: +86-25-80821044; E-mail: yxfrp@yahoo.com.cn
- Crack tip higher order stress fields for functionally graded materials with generalized form of gradation


