
Influence of Nb and Mo contents on phase stability and elastic property of β-type Ti-X alloys
YAO Qiang(姚 强), SUN Jian(孙 坚), XING Hui(邢 辉), GUO Wen-yuan(郭文渊)
School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
Received 15 July 2007; accepted 10 September 2007
Abstract:
The energetic, electronic structure and elastic property of β-type Ti1-xXx (X=Nb and Mo, x=0.041 7, 0.062 5, 0.125 0, 0.187 5, 0.250 0, 0.312 5 and 0.375) binary alloys were calculated by the method of supercell and augmented plane waves plus local orbitals within generalized gradient approximation. The elastic moduli of the polycrystals for these Ti1-xXx alloys were calculated from the elastic constants of the single crystal by the Voigt-Reuss-Hill averaging method. Based on the calculated results, the influence of X content on the phase stability and elastic property of β-type Ti1-xXx alloys was investigated. The results show that the phase stability, tetragonal shear constant C′, bulk modulus, elastic modulus and shear modulus of β-type Ti1-xXx alloys increase with an increase of X content monotonously. When the valence electron number of β-type Ti1-xXx alloys is around 4.10, i.e. the content of Nb is 9.87% (molar fraction) in the Ti-Nb alloy and Mo is 4.77% (molar fraction) in Ti-Mo alloy, the tetragonal shear constant is nearly zero. The Ti1-xXx alloys achieve low phase stability and low elastic modulus when the tetragonal shear constant reaches nearly zero. In addition, the phase stability of β-type Ti1-xXx alloys was discussed together with the calculated electronic structure.
Key words:
Ti alloy; elastic property; phase stability; electronic structure; First-Principle;
1 Introduction
Ti alloys have been used in various engineering fields, such as automobile, chemical and aerospace industries, because they exhibit excellent physical and chemical properties[1-2]. It is well known that titanium metal exhibits a hexagonal close packed structure (α) with spacegroup P63/mmc at room temperature but transforms to a body centered cubic phase (β) with spacegroup ![]() at high temperature. Recently, the β-type and metastable β-type Ti-base alloys containing Nb and Mo transition elements have been investigated as load-bearing orthopaedic implants due to their low elastic modulus, good biocompatibility and long lifetime in the human body[3]. However, the relationship among mechanical property, phase stability and electronic structure in the low elasticity Ti alloys has not been clear. Recently, the computer-aided material design becomes a research hotspot. KURODA et al[4] designed a series of new β-type Ti-base alloys using the d-electron alloy design method and investigated their mechanical properties systematically. They found that the phase constituent and mechanical property of Ti alloys are correlated with two electronic parameters, i.e. bond order and d-orbital energy level. A correlation between the phase stability and the elastic properties in β-type Ti-base alloys was investigated with the aid of above two electronic parameters by ABDEL-HADY et al[5]. But this method doesn’t clearly describe the physical basis of the relationship between the mechanical property and electronic parameter. In addition, IKEHATA et al[6] studied the elastic properties of the Ti1-xXx (X=Nb, V, Ta, Mo and W, x= 0, 0.25, 0.50, 0.75 and 1.00) binary alloys by the ultrasoft pseudopotential method within generalized gradient approximation. Their results showed that the rigid band model can be applied to investigate elastic properties of Ti1-xXx alloys and the valence electron number per atom is an important parameter to describe the elastic characteristics of the alloys.
at high temperature. Recently, the β-type and metastable β-type Ti-base alloys containing Nb and Mo transition elements have been investigated as load-bearing orthopaedic implants due to their low elastic modulus, good biocompatibility and long lifetime in the human body[3]. However, the relationship among mechanical property, phase stability and electronic structure in the low elasticity Ti alloys has not been clear. Recently, the computer-aided material design becomes a research hotspot. KURODA et al[4] designed a series of new β-type Ti-base alloys using the d-electron alloy design method and investigated their mechanical properties systematically. They found that the phase constituent and mechanical property of Ti alloys are correlated with two electronic parameters, i.e. bond order and d-orbital energy level. A correlation between the phase stability and the elastic properties in β-type Ti-base alloys was investigated with the aid of above two electronic parameters by ABDEL-HADY et al[5]. But this method doesn’t clearly describe the physical basis of the relationship between the mechanical property and electronic parameter. In addition, IKEHATA et al[6] studied the elastic properties of the Ti1-xXx (X=Nb, V, Ta, Mo and W, x= 0, 0.25, 0.50, 0.75 and 1.00) binary alloys by the ultrasoft pseudopotential method within generalized gradient approximation. Their results showed that the rigid band model can be applied to investigate elastic properties of Ti1-xXx alloys and the valence electron number per atom is an important parameter to describe the elastic characteristics of the alloys.
In this study, the method of supercell and augmented plane-wave plus local orbitals within the generalized gradient approximation was used to calculate the total energy of the Ti-X (X=Nb and Mo) binary alloys with β structure. The cohesive energy, phase stability and elastic property of the β-type Ti-X binary alloys were investigated. The electronic structures of these β-type Ti-X binary alloys were also calculated and applied to discuss the phase stability of β-type Ti-X binary alloys. 2 Computational details
The Wien2k software package was utilized to calculate the total energies, elastic properties and electronic structures of the β-type Ti-X (X=Nb and Mo) binary alloys[7]. The method of augmented plane wave plus local orbitals (APW+LO) method was selected, where the core states are treated fully relativistically, and the semi-core and valance states are in a scalar relativistic approximation[8]. Inside the atomic spheres the potential and charge densities are expanded in lattice harmonics up to L=10. Exchange and correlation effects are treated within density functional theory, using the generalized gradient approximation(GGA)[9]. The muffin-tin radius of 2.2 a.u. was chosen for Mo, and 2.3 a.u. for Ti and Nb, respectively. A plane-wave cutoff (RmtKmax) of 7.0 was used. The calculations were performed with 1000 k-point mesh in the Brillouin zone. The Brillouin zone integration was carried out using a modified tetrahedron method[10]. Convergence was assumed when the energy difference was less than 0.1 mRy. The calculations were performed without spin polarization.
In order to calculate the total energies, elastic properties and electronic structures of the β-type Ti-X binary alloys with different alloying contents, the supercell method was employed in the present calculation. A 16-atom supercell that contains eight BCC unit cells was constructed. When n (n=1-6) X atom substitutes the Ti atom in the supercell, the chemical formula is assumed as Ti1-xXx (x=0.062 5, 0.125 0, 0.187 5, 0.250 0, 0.312 5 and 0.375). In addition, a 24-atom 2×2×3 supercell containing one Mo atom was adopted to calculate the total energy and elastic property of the Ti1-xMox (x=0.0417) binary alloy.
3 Results and discussion
First of all, calculations of total energies as a function of cell volume were carried out to optimize the lattice constant of the Ti1-xXx binary alloys. The equilibrium lattice constant and bulk modulus were derived directly from these calculations. The calculated equilibrium lattice constants of Ti1-xNbx and Ti1-xMox alloys are plotted in Fig.1. It can be seen from Fig.1 that the lattice constants of Ti1-xNbx increase monotonously with increasing the content of Nb, while the lattice constants of Ti1-xMox decrease monotonously with an increase of Mo content. The reason for causing above phenomenon is that the diameter of Ti atom is larger than that of Mo atom and smaller than that of Nb atom. The cohesive energies for Ti1-xNbx and Ti1-xMox alloys are calculated, since the cohesive energy directly reflects the phase stability of Ti1-xNbx and Ti1-xMox alloys. Fig.2 shows the cohesive energies for Ti1-xNbx and Ti1-xMox alloys. It can be seen from Fig.2 that the cohesive energies of Ti1-xNbx and Ti1-xMox alloys increase monotonously with increasing the contents of Nb and Mo, respectively. These imply that the phase stability of β-type Ti1-xNbx and Ti1-xMox alloys can be improved by increasing Nb and Mo contents, respectively.
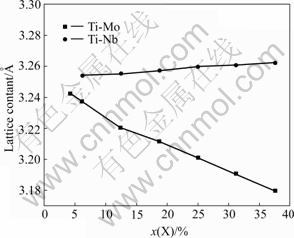
Fig.1 Relationship between lattice constant and X content
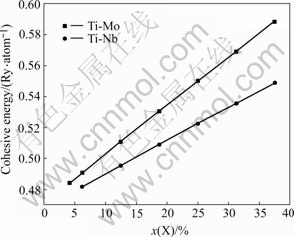
Fig.2 Relationship between cohesive energy and X content
The density of states(DOS) for the binary Ti1-xNbx and Ti1-xMox alloys was further calculated, which provided information on the physical basis of the phase stability. Fig.3 shows the total density of states of the binary Ti1-xNbx (x=0.125, 0.250 and 0.375) and Ti1-xMox (x=0.125, 0.250 and 0.375) alloys. The DOS curves of the Ti1-xNbx and Ti1-xMox are almost the same as those reported by IKEHATA et al[6]. There is a pronounced pseudogap between the low-energy bonding and high-energy anti-bonding regions in each DOS spectrum for Ti1-xNbx and Ti1-xMox. Furthermore, the Fermi level is located in the bonding region of the DOS spectrum. This means that the phase stability of the β structure is relatively low in Ti1-xNbx and Ti1-xMox alloys. It can also be seen from Fig.3 that the low-energy bonding peaks shift towards the lower energy with increasing the contents of Nb and Mo in the DOS spectra of Ti1-xNbx and Ti1-xMox, respectively. This implies that the phase stability of β-type Ti1-xNbx and Ti1-xMox alloys can be enhanced by increasing the Nb and Mo contents, respectively.
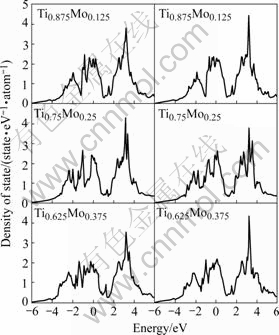
Fig.3 Density of states of Ti1-xXx (X=Mo and Nb, x=0.125, 0.250, 0.375)
To calculate the elastic constants of β-type Ti1-xNbx and Ti1-xMox alloys using the total energies, a new distorted cell is introduced by imposing deformations on the initial cell. The elastic strain energy is given by
![]()
![]()
![]() (1)
(1)
where DE is the total energy difference between the distorted and initial cells, V0 the equilibrium cell volume, Cij the elastic constant and ei, j the strain. For the cubic structure, only three elastic constants, namely C11, C12 and C44 are independent. In order to calculate the C11 and C12, we take a volume-conserving orthorhombic distortion, where the strain tensor ε is written as
 (2)
(2)
The strain energy U for an orthorhombic distortion is described by
U=(C11-C12)e2+O(e4) (3)
There is another relation between C11 and C12, that is
B=![]() (4)
(4)
where B is the bulk modulus.
C44 can be calculated by putting a volume- conserving monoclinic distortion, where the strain tensor ε is given by
 (5)
(5)
The strain energy U for a monoclinic distortion is defined by
U=![]() C44e2 + O(e4) (6)
C44e2 + O(e4) (6)
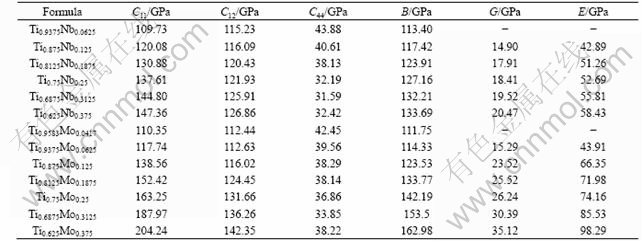
The calculated elastic constants of the Ti1-xNbx and Ti1-xMox alloys are listed in table 1. The elastic moduli and shear moduli of the Ti1-xNbx and Ti1-xMox alloys can be calculated from the elastic constants in table 1. Note that the elastic moduli in table 1 are Hill’s averages. The Hill’s average is the arithmetic mean of the VOIGT average and REUSS average[11]. In the VOIGT average, the shear modulus is given by
Gv=![]() (7)
(7)
while in the Reuss average it is given by
GR=![]() (8)
(8)
where Sij is the inverse matrix of Cij with the relations C44=1/S44, C11-C12=(S11-S12)-1 and C11+2C12=(S11+2S12)-1. The elastic modulus is given by
E=![]() (9)
(9)
It can be seen from the Table 1 that C11, C12, B, G and E of Ti1-xNbx and Ti1-xMox increase monotonously with increasing the Nb and Mo contents, respectively. However, the relationship between C44 and alloying content is not clear. In combination with Fig.1 and Table 1, it can be deduced that lattice expansion or lattice shrinkage of Ti1-xXx alloys does not have correlation with the change trend of elastic moduli of Ti1-xXx. It is known that for cubic crystals, the elastic stability requires the elastic stiffness constants satisfying the following conditions[12]:
Table 1 Elastic properties of Ti1-xNbx and Ti1-xMox
C44>0, C11+2C12>0, C11-|C12|>0
Therefore, the tetragonal elastic constant C′=(C11-C12)/2 can represent the elastic stability of cubic crystal. The tetragonal elastic constants of Ti1-xNbx and Ti1-xMox alloys are plotted in Fig.4. It can be seen from Fig.4 that tetragonal elastic constants of Ti1-xNbx and Ti1-xMox increase monotonously with increasing the contents of Nb and Mo, respectively. When the content of Nb is 9.87% (molar fraction) in the Ti-Nb alloy and Mo is 4.77%(molar fraction) in the Ti-Mo alloy, i.e. the valence electron number per atom of Ti1-xXx alloys is around 4.10, the tetragonal shear constants of Ti1-xXx are nearly zero. In other words, when the valence electron number per atom of Ti1-xXx alloys is 4.10 or more, the Ti1-xXx with β structure is stable. LI et al[13] investigated the elastic properties of Ti-V alloy by the First Principles calculation, and they found that the Ti-V alloy with BCC structure is unstable when the valence electron number per atom of Ti-V alloy is less than 4.10. Their results are in good agreement with the present calculated results. Generally speaking, if the content of β-phase stabilizing elements (e.g. Mo and Nb) doesn’t exceed a critical amount in the Ti-X binary alloys, three kinds of metastable phase transformation (β→α′, α″ and ω) can be conducted through different heating treatment processes. HO et al[14] studied the structure and properties of a series of cast binary Ti-Mo alloys. Their results showed that the alloy is dominated by the martensitic α″ phase when Mo content is 3.89% (molar fraction). When Mo content is increased to 4.7% (molar fraction), α″ phase and β phase are observed in the alloy. When Mo content is higher than 5.25% (molar fraction), β phase becomes the only dominant phase. The present calculated results for the Ti1-xMox alloy are the same as experimental results. In addition, LEE et al[15] investigated the microstructure of a series of cast binary Ti-Nb alloys. Their results indicated that when Nb content is 8.33% (molar fraction), the alloy is primarily composed of α″ phase. When Nb content is 16.35% (molar fraction), metastable β phase starts to be retained. When Nb content is 21.72% (molar fraction) or higher, β phase becomes the only dominant phase. However, the present calculated results show that when the content of Nb is 9.87% (molar fraction), β phase is stable in Ti-Nb alloy. In fact, the occurrence of β phase in Ti1-xXx alloys would depend not only on the phase stability but also on the competition of phase stability of different phases. Therefore, in titanium alloy design for the low elastic modulus, the addition of several molar fraction of alloy-ing elements is required to suppress the occurrence of the α″ and ω phases.

Fig.4 Relationship between tetragonal shear constant C′ and X content
4 Conclusions
1) The phase stability, tetragonal shear constant C′, bulk modulus, elastic modulus and shear modulus of β-type Ti1-xXx alloys increase with increasing of X content monotonously.
2) When the valence electron number of the Ti1-xXx alloys is around 4.10, i.e. the content of Nb is 9.87% (molar fraction) in the Ti-Nb alloy and Mo is 4.77% (molar fraction) in the Ti-Mo alloy, the tetragonal shear constant C′ is nearly zero.
3) The Ti1-xXx alloys achieve low phase stability and low elastic modulus when the tetragonal shear constant C′ reaches nearly zero.
References
[1] COLLINGS E W. Physical metallurgy of titanium alloys [M]. Ohio: ASM, 1984.
[2] BOYER R R, BRIGGS R D. The use of beta titanium alloys in the aerospace industry [J]. J Mater Eng Perform, 2005, 14(6): 681-685.
[3] RACK H J, QAZI J I. Titanium alloys for biomedical applications [J]. Mater Sci Eng C, 2006, 26(8): 1269-1277.
[4] KURODA D, NIINOMI M, MORINAGA M, KATO Y, YASHIRO T. Design and mechanical properties of new β type titanium alloys for implant materials [J]. Mater Sci Eng A, 1998, 243: 244-249.
[5] ABDEL-HADY M, HINOSHITA K, MORINAGA M. General approach to phase stability and elastic properties of β-type Ti-alloys using electronic parameters [J]. Scripta Mater, 2006, 55: 477-480.
[6] IKEHATA H, NAGASAKO N, FURUTA T, FUKUMOTO A, MIWA K, SAITO T. First-Principles calculations for development of low elastic modulus Ti alloys [J]. Phys Rev B, 2004, 70: 174113.
[7] SCHWARZ K, BLAHA P, MADSEN G K H. Electronic structure calculations of solids using the WIEN2k package for material sciences [J].Comput Phys Commun, 2002, 147(1/2): 71-76.
[8] MADSEN G K H, BLAHA P, SCHWARZ K, SJOSTEDT E, NORDSTROM L. Efficient linearization of the augmented plane-wave method [J]. Phys Rev B, 2001, 64(19): 195134.
[9] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Phys Rev Lett, 1996; 77: 3865-3868.
[10] BLOCHL P E, JEPSEN O, ANDERSON O K. Improved tetrahedron method for Brillouin-zone integrations [J]. Phys Rev B, 1994, 49(23): 16223-16233.
[11] ANDERSON O L. A simplified method for calculating the Debye temperature from elastic constants [J]. J Phys Chem Solids, 1963, 24: 909-917.
[12] BORN M, HUANG K. Dynamical theory of crystal lattices [M]. Oxford: Clarendon Press, 1954: 141.
[13] LI T S, MORRIS J W, NAGASAKO N, KURAMOTO S, CHRZAN D C. Ideal engineering alloys [J]. Phys Rev Lett, 2007, 98: 105503.
[14] HO W F, JU C P, CHERN-LIN J H. Structure and properties of cast binary Ti-Mo alloys [J]. Biomaterials, 1999, 20: 2115-2122.
[15] LEE C M, JU C P, CHERN-LIN J H. Structure-property relationship of cast Ti-Nb alloys [J]. J Oral Rehabil, 2002, 29: 314-322.
(Edited by YANG Bing)
Foundation item: Project(50571063) supported by the National Natural Science Foundation of China; Project(04JC14054) supported by the Science and Technology Committee of Shanghai, China
Corresponding author: SUN Jian; Tel: +86-21-54745593; E-mail: jsun@sjtu.edu.cn


