分离变量时滞微分系统的指数稳定性
蹇继贵, 孔德明, 罗海庚, 廖晓昕
(华中科技大学 控制科学与工程系, 湖北 武汉, 430074)
摘要: 讨论了一类具有有界可变时滞分离变量系统平衡点的全局指数稳定性。在所给函数为Lipschitz连续的情况下,利用Lyapunov 函数方法并结合Halanay时滞微分不等式,分别构造适当的连续但不一定可微的数量或向量Lyapunov函数和二次型Lyapunov函数,获得了几个保证此类分离变量型时滞系统的平衡点为全局指数稳定的时滞相关和时滞无关的代数判据。这些判据将问题化为代数不等式或M矩阵,可以直接根据系统方程进行检验,便于实际应用。
关键词: 非线性时滞系统;全局指数稳定性;时滞微分不等式;分离变量;时变时滞
中图分类号:O173.13 文献标识码:A 文章编号: 1672-7207(2005)02-0282-06
Exponential Stability of Differential Systems with Separated Variables and Time Delays
JIAN Ji-gui, KONG De-ming, LUO Hai-geng, LIAO Xiao-xin
(Department of Control Science and Engineering,Huazhong University of Science and Technology, Wuhan 430074, China)
Abstract: The global exponential stability of equilibrium states of a class of nonlinear separated variables systems with bounded time-varying delays was investigated. Based on Lipschitz continuous functions and Lyapunov functions method and the Halanays delay differential inequality, some algebraic criterions of globally exponential stability for the type of systems are obtained via constructing appropriate continuous and non-differential scalar and vector Lyapunov functions and quadratic form Lyapunov function, respectively, whose results are both independent of and dependent on the magnitudes of the delays. These criteria reduce the problem to a set of algebraic inequalities or M matrix and can be verified directly according to equation of the concerned systems, and therefore are convenient in practical use.
Key words: nonlinear delay system; global exponential stability; delay differential inequality; separated variables; time-varying delay
-
在自动控制理论及神经网络理论中,带时滞的分离变量系统是最常见也是最常用的系统,如时滞Hopfield神经网络模型[1-5]、时滞生态系统[6]、时滞BAM模型[7]、时滞Lurie模型[8-10]。而时滞Lurie模型可化为时滞可分离变量系统[8-10]。通过对分离变量系统的理论及应用研究[11-14],其结果主要是关于系统平凡解的全局稳定性结果。人们对其平凡解的指数稳定性研究结果较少[12],而在对如前所述的各类模型的实际应用中,由于其指数稳定性能较好[CM(22] 地保证平凡解的收敛行为,如收敛速度和时间估计等,因而有必要对时滞可分离变量系统的指数稳定性行为进行研究。在此,作者基于文献[1,15]的基本思想,利用Halanay不等式和Lyapunov函数,讨论一类有界可变时滞分离变量系统的指数稳定性。
1 模型的描述及引理
考虑n维非线性分离变量系统:
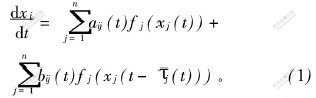
其中:i=1,2,…,n;j=1,2,…,n;0≤τj(t)≤τ;τ为常数;aij(t),bij(t)在(t0-τ,+∞)上连续且有界;fj(0)=0,fj(xj)∈C[R,R],其初始条件为xi(t)=φi(t),t∈[t0-τ,t0],函数φi(t)为连续有界函数。保证系统(1)的解存在惟一性,且满足条件:
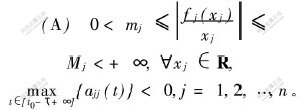
当aij(t)=aij,bij(t)=bij均为常数时,系统(1)化为更常用的系统:
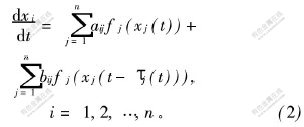
记|x|=|x1|,…,|xn|)T; M=diag(M1, …,Mn)
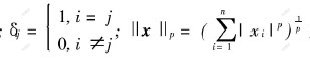
为向量x的p范数,这里p=1,2。
定义1 称系统(1)的平凡解是全局指数稳定的,若存在常数λ>0和M≥1使得系统(1)的任意解x(t)满足:
![]()
引理1[1] 若存在2个常数r1>r2>0,x(t)是[t0-τ,t0]上定义的非负连续数量函数,且在此区间上有D+x(t)≤-r1x(t)+r2[AKx-](t)。其中
![]() ,
,
常数τ≥0;则当t≥t0时,有x(t)≤![]() 。其中,λ为代数方程λ=r1-r2eλτ的惟一正根。
。其中,λ为代数方程λ=r1-r2eλτ的惟一正根。
引理2[1] 设A=(aij)n×n和B=(bij)n×n为实方阵并满足:
![]()
其中:
![]() ,
,
aij≥0,i≠j;bij≥0,i=1,2,…,n;j=1,2,…,n;
b.矩阵M=-(A+B)为M矩阵。
则存在1个常向量η=(η1,η2,…,ηn)T>0,和一个常数α>0,使不等式组(3)的解x(t)满足估计式:
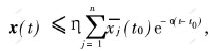
或
![]()
2 全局指数稳定性结果
定理1 若条件(A)成立,且系统(1)还满足:
a. fj(xj(t))xj(t)>0,xj(t)≠0,j=1,2,…,n;
b.存在1个正对角矩阵D=diag(d1,…,dn)>0使得:
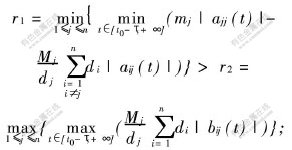
则系统(1)的平凡解全局指数稳定。
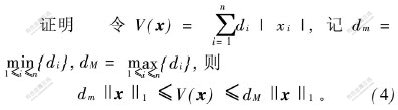
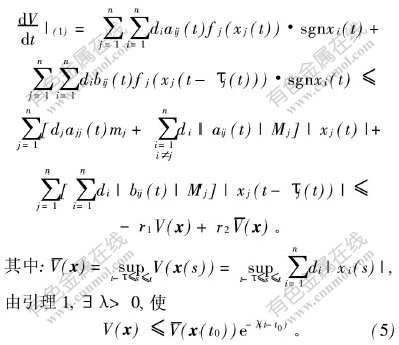
结合式(4)和式(5)得:
![]()
由定义1知系统(1)的平凡解全局指数稳定。
推论1 若条件(A)成立,且系统(2)满足:
a. fj(xj(t))xj(t)>0, xj(t)≠0, ajj〈0,j=1,2,…, n;
b. 存在1个正对角矩阵D=diag(d1, …,dn)>0,使得:
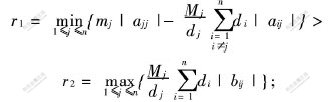
则系统(2)的平凡解全局指数稳定。
定理2 若条件(A)成立,且系统(1)满足:
a. fj(xj(t))xj(t)>0(xj(t)≠0), j=1,2,…,n;
b. 存在1个正对角矩阵D=diag(d1,…,dn)>0,使得矩阵![]() 负定。其中:
负定。其中:
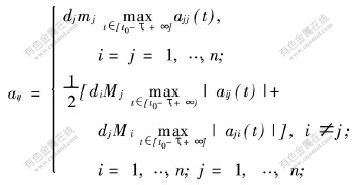
c.
![]() 。
。
其中:
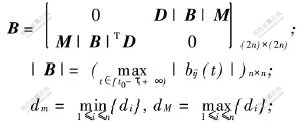
![]() 分别为矩阵A[TX~]和B[TX~]的最大特征值。则系统(1)的平凡解全局指数稳定。
分别为矩阵A[TX~]和B[TX~]的最大特征值。则系统(1)的平凡解全局指数稳定。
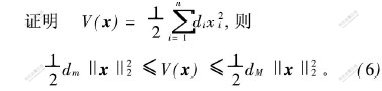
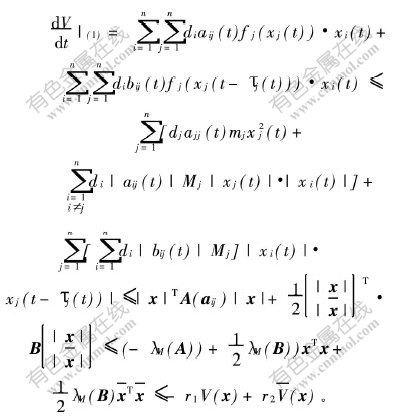
其中: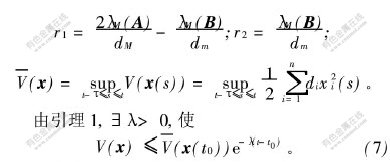
结合式(6)和式(7)得:
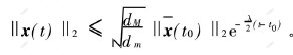
由定义1知结论成立。
推论2 若条件(A)成立,且系统(2)满足:
a. fj(xj(t))xj(t)>0(xj(t))≠0),ajj〈0,j=1,2,…,n;
b. 存在1个正对角矩阵D=diag(d1,…,dn)>0,使得矩阵![]() 负定。其中:
负定。其中:
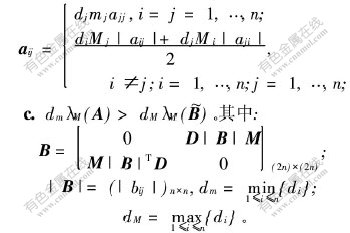
![]()
分别为矩阵A[TX~]和B[TX~]的最大特征值。则系统(2)的平凡解全局指数稳定。
当n较大时,要求出-λM(A[TX~])与λM(B[TX~])较困难。
推论3 若条件(A)成立,且系统(2)满足:
a. fj(xj(t))xj(t)>0(xj(t)≠0), ajj〈0,j=1,2,…,n;
b. r1+r2+r3〈0。其中: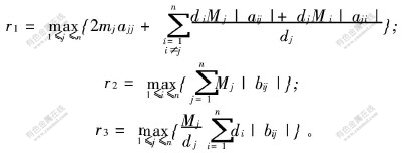
则推论2的结论成立。
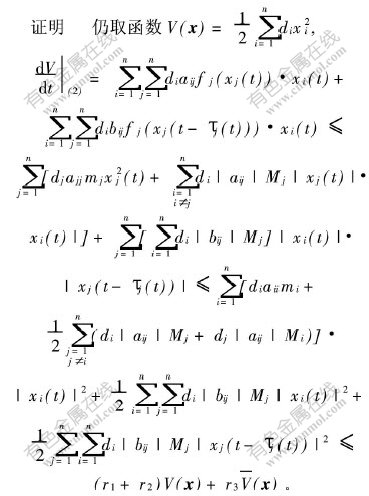
由引理1和定理2可知该结论成立。
下面通过向量Lyapunov函数来讨论系统(2)的
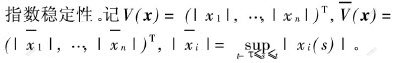
定理3 若条件(A)成立,且系统(2)满足:
a. fj(xj(t))xj(t)>0,xj(t)≠0,ajj〈0,j=1,2,…,n;
b. 矩阵-(A+B)为M矩阵。其中:
A=(-|aii|miδij+(1-δij)|aij|Mj)n×n;
B=(|bij|Mj)n×n。
则系统(2)的平凡解全局指数稳定。
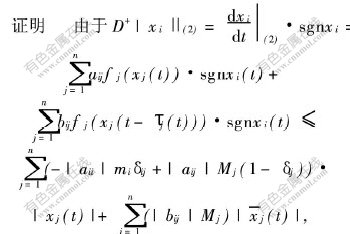
即
![]()
由引理2有,存在ηi>0(i=1,2,…,n),α>0使系统(2)的解有估计式:
![]()
式(8)表明系统(2)的零解全局指数稳定。
定理4 若条件(A)成立,且系统(2)满足
a. fj(xj(t))xj(t)>0,xj(t)≠0,ajj〈0,j=1,2,…,n;
b. 存在常数λ>0使矩阵((|aii|mi-λ)δij-(1-δij)|aij|Mj-|bij|Mjeλτ)n×n为M矩阵,则系统(2)的平凡解全局指数稳定,且收敛指数至少为λ。
证明 令|yi(t)|=|xi(t)|eλτ,则
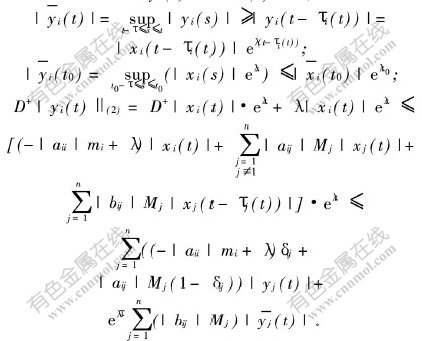
由定理3,存在ηi>0,α>0,使系统(2)的解有估计式:
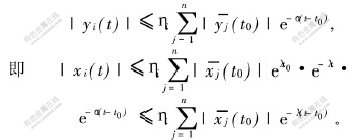
上式表明所证结论成立。
定理5 若条件(A)成立,且系统(2)满足:
a.fj(xj(t))xj(t)>0, xj(t)≠0, ajj〈0, j=1,2,…n;
b. 存在常数δ>0,使1-τ′j(t)≥δ>0, j=1,2,…,n;
c.存在常数αj>0(j=1,2,…,n)及λ>0,满足:
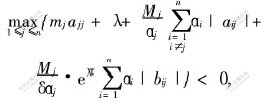
则系统(2)的平凡解全局指数稳定,且收敛指数至少为λ。
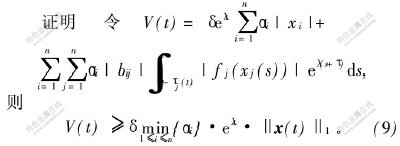
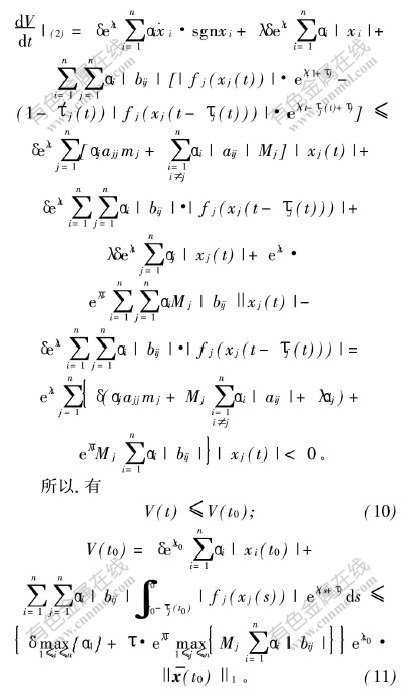
由式(9)、式(10)和式(11)得:
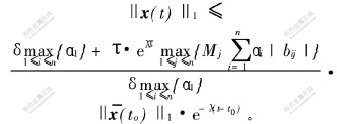
上式说明所证结论成立。
3 仿真实例
考虑系统
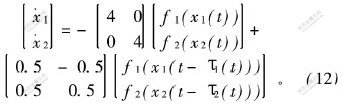
其中
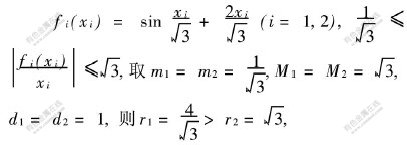
根据推论1,系统(12)的零解全局指数稳定。
又由于
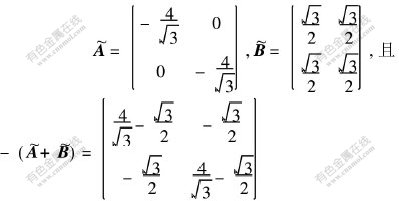
为M矩阵,定理3的条件全部满足,从而由定理3也可判定系统(12)的零解全局指数稳定。
对于初值x0=(8,-7),取常时滞τ1(t)=1,τ2(t)=2和变时滞τ1(t)=1+0.5sint,τ2(t)=0.5+0.25exp(-sint)时的轨线走向分别如图1和图2所示,可见,该仿真曲线表明了定理3结论的正确性。
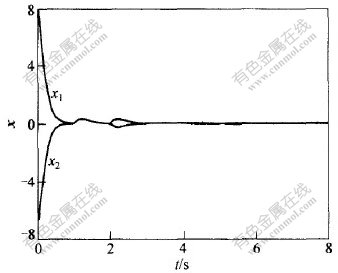
图 1 常时滞时的轨线走向
Fig. 1 Trajectory curve of system(12) for constant delay
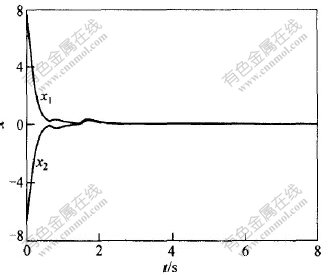
图 2 变时滞时的轨线走向
Fig. 2 Trajectory curve of system(12) for variables delay
参考文献:
[1] 廖晓昕, 肖冬梅. 具有变时滞的Hopfield型神经网络的全局指数稳定性[J]. 电子学报, 2000, 28(4): 87-90.
LIAO Xiao-xin, XIAO Dong-mei. Globally Exponential Stability of Hopfield Neural Networks with Time-varying Delays[J]. Acta Electronica Sinica, 2000, 28(4): 87-90.
[2]LIAO Xiao-xin, WANG Jun. Algebraic Criteria for Globally Exponential Stability of Cellular Neural Networks with Multiple Time Delays [J]. IEEE Transactions on Circuits and Systems—I: Fundamental Theory and Applications, 2003,50(2): 268-275.
[3]ZHANG Ji-ye. Globally Exponential Stability of Neural Networks with Variable Delays[J]. IEEE Transactions on Circuits and Systems—I: Fundamental Theory and Applications, 2003, 50(2): 288-291.
[4]ZHOU Dong-ming, CAO Jin-de. Globally Exponential Stability Conditions for Cellular Neural Networks with Time-varying Delays[J]. Applied Mathematics and Computation, 2002, 131: 487-496.
[5]SUN Chang-yin, ZHANG Kan-jian, FEI Shu-min, et al. On Exponential Stability of Delayed Neural Networks with a General Class of Activation Functions [J]. Physics Letters A, 2002, 298:122-132.
[6]LIAO Xiao-xin, LI Jia. Robust Interval Stability, Persistence and Partial Stability on Lotka-volterra Systems with Time-delay[J]. Applied Mathematics and Computation, 1996, 75:103-115.
[7]LIAO Xiao-feng, YU Jue-bang. Qualitative Analysis of Bi-directional Associative Memory Networks with Time Delays[J]. International Journal of Circuits Theory and Applications, 1998, 26:219-229.
[8]年晓红. 具有时滞的Lurie型控制系统的绝对稳定性[J]. 西北师范大学学报(自然科学版),1997,33(1): 9-14.
NIAN Xiao-hong. Absolute Stability of Lurie Control Systems with time Delay[J]. Journal of Northwest Normal University (Natural Science), 1997,33 (1): 9-14.
[9]年晓红. Lurie控制系统绝对稳定的时滞相关条件[J]. 自动化学报, 1999, 25(4): 564-566.
NIAN Xiao-hong. Delay Dependent Conditions for Absolute Stability of Lurie Type Control Systems [J]. Acta Automatica Sinica, 1999, 25(4): 564-566.
[10]徐炳吉, 廖晓昕. Lurie控制系统的时滞相关绝对稳定性判据[J]. 自动化学报, 2002, 28(2): 317-320.
XU Bing-ji, LIAO Xiao-xin. Absolute Stability Criteria of Delay Dependent for Lurie Control Systems [J]. Acta Automatica Sinica, 2002, 28(2): 317-320.
[11]廖晓昕. 稳定性的数学理论及应用 (第2版)[M]. 武汉: 华中师范大学出版社, 2001.
LIAO Xiao-xin. Mathematical Theory and Applications of Stability(2nd Ed)[M]. Wuhan: Huazhong Normal University Press, 2001.
[12]王美娟. 具有分离变量型的非线性滞后型系统解的指数稳定性[J]. 工程数学学报, 1996, 13(4) :15-20.
WANG Mei-juan. The Exponential Stability of Nonlinear Delay System Which Has Separable Variables [J]. Journal of Engineering Mathematics, 1996, 13(4): 15-20.
[13]吴晓非. 具有分离变量的非线性微分系统稳定性的一些新结果[J]. 应用数学, 1996, 9(4):503-506.
WU Xiao-fei. Some Results of Stability for Nonlinear Differential Systems with Separated Variables [J]. Mathematica Applicata, 1996, 9(4): 503-506.
[14]LIU Bi-yu, Gui Wei-hua. Stabilization Controller for a Class of Nonlinear Discrete Control Systems with Separated Variables [J]. Mathematical Theory and Applications, 2003, 23(3): 53-56.
[15]ZENG Zhi-gang, FU Chao-jin, LIAO Xiao-xin. A Delay Differential Inequality[J]. Annals of Differential Equations, 2002,18(4): 425-430.
收稿日期:2004-06-10
基金项目:国家自然科学基金资助项目(60274007, 60474011); 教育部博士点基金资助项目(20010487005)
作者简介:蹇继贵(1965-),男,四川苍溪人,副教授,博士研究生;从事动力系统稳定性及神经网络理论研究
论文联系人: 孔德明,男,讲师,博士研究生;电话:0731-2655093(H); E-mail: kong1971@163.com


