DOI: 10.11817/j.issn.1672-7207.2018.07.014
基于量子计算加速的DDC算法
刘雪娟,袁家斌,许娟,段博佳
(南京航空航天大学 计算机科学与技术学院,江苏 南京,210016)
摘 要:
具有超强的并行计算能力,拟引入量子计算以降低局部密度和delta距离度量的聚类算法(DDC)计算复杂度。DDC算法的局部密度求解过程是计数算法,提出利用量子计数算法加速局部密度的求解;delta距离是最小值查找的过程,提出利用最小值查找量子算法加速delta距离的求解。研究结果表明:利用量子计算对DDC聚类算法进行加速,能够使算法的执行效率获得显著提升。
关键词:
中图分类号:TP387 文献标志码:A 文章编号:1672-7207(2018)07-1677-06
Speed up DDC based on quantum computing
LIU Xuejuan, YUAN Jiabin, XU Juan, DUAN Bojia
(College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
Abstract: The purpose was to improve the efficiency of local density and delta distance based clustering (DDC) by using the quantum computation, which was characterized by the great performance of the parallel computation. First, the quantum counting algorithm was developed to accelerate the processing of local density for each data point. Then, the quantum algorithm for finding the minimum was incorporated to find each point’s delta distance. The results show that the efficiency of DDC can be improved significantly by using quantum computation to accelerate DDC algorithm.
Key words: local density; delta distance; clustering algorithm; quantum computation; speed up
聚类作为一种常见的数据分析处理技术,依据一定的相似性度量将数据划分成若干类,以发现其中潜在的规律[1],其广泛应用于图像处理、模式识别和社交网络等领域。常见的聚类算法或存在易陷于局部极值、对初始值敏感、不能自动确定簇的数量或存在严重依赖数据分布等缺点[2],如k-means,FCM和DBSCAN等。RODRIGUEZ等[3]提出一种基于局部密度和delta距离度量的聚类算法(density & distance clustering,DDC)。与其他聚类算法相比较,DDC聚类算法具有数据分布自适应、无需设置初始值且能自动识别簇的数量等优点,其一经提出便得到聚类研究者的极大关注及广泛应用。CHENG等[4]将DDC算法用于超网络中的社群检测中,通过利用DDC算法计算超网络中各节点的密度和距离来构建一种称为密度排序树的结构(density-ordered tree, DOT)以表示原始数据,使社群检测问题转换成DOT划分问题。CHEN等[5]将DDC算法应用于面部年龄的估计中,先将面部特征转换为LBP 集合,利用DDC算法从LBP集合中发现每个年龄组的密度峰值,根据到密度峰值的距离来估计每张面部图片的年龄。WANG等[6]将DDC算法用于社交网络,利用DDC算法计算社交网络中每个用户的距离和密度以发现其所属的社交圈。在现今的大数据时代,巨大的数据量为聚类的速度带来了巨大的挑战,为应对这种挑战,目前较为普遍的策略是采用云计算的模式对大数据进行并行聚类[7]。可是,云计算的硬件基础设施所产生的巨大的能量消耗问题又带来新的挑战[8-9]。考虑到量子计算具有超强的并行计算能力,计算的可逆性也不会带来面临能量消耗问题[10],近年来,量子计算受到研究者越来越多的关注,并被应用到各个领域以达到加速的目的[11-15]。DDC作为一种具有全新的、聚类效果优良的算法,目前为止仍未检索到量子计算对其加速的研究,本文提出利用量子计算的相关理论加速DDC算法。 提出分别利用量子计数算法和最小值量子查找算法去加速DDC算法中的局部密度和delta距离这2个参数的计算,使其在大数据环境下不但聚类效果优良,且聚类速度更快。
1 基础知识
1.1 DDC算法
DDC算法的聚类过程主要是计算每个数据点的局部密度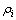 和delta距离
和delta距离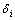 ,选取局部密度和delta距离值都较大的数据点作为聚类中心点,其中
,选取局部密度和delta距离值都较大的数据点作为聚类中心点,其中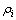 为数据点
为数据点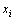 到其余各点距离
到其余各点距离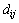 小于
小于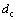 的个数,
的个数,
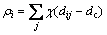 (1)
(1)
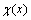 为符号函数,
为符号函数,
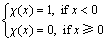 (2)
(2)
局部密度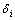 为比其局部密度大的数据点的距离最小值,
为比其局部密度大的数据点的距离最小值,
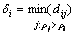 (3)
(3)
DDC算法计算所有数据点的局部密度和delta距离所需的时间复杂度均为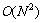 。在大数据环境下,该算法计算量较大,聚类速度较慢,故研究利用量子计算加快DDC算法的聚类速度。
。在大数据环境下,该算法计算量较大,聚类速度较慢,故研究利用量子计算加快DDC算法的聚类速度。
1.2 量子算法
Grover是一种量子搜索算法,其从给定的集合中找到目标元素x,使其满足函数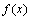 为真。该算法利用量子叠加态的性质,反复利用量子黑箱进行操作,使目标态的概率幅变大,非目标态的概率幅减小,其中用于搜索的量子黑箱O定义为
为真。该算法利用量子叠加态的性质,反复利用量子黑箱进行操作,使目标态的概率幅变大,非目标态的概率幅减小,其中用于搜索的量子黑箱O定义为
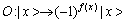
Grover算法搜索的过程为:从计算机的初态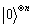 开始,通过Hadamard变换使所有基态的概率幅相等,即量子态处于均衡叠加态:
开始,通过Hadamard变换使所有基态的概率幅相等,即量子态处于均衡叠加态:
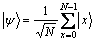
接下来迭代执行以下4步,迭代过程称之为Grover迭代:
1) 应用量子黑箱O;
2) 应用Hadamard变换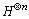 ;
;
3) 执行条件相移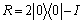 ,使
,使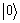 以外的每个计算基态的概率幅相位取反;
以外的每个计算基态的概率幅相位取反;
4) 应用Hadamard变换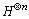 。
。
Grover迭代执行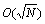 次后,可以很高的概率得到目标解[16-17]。Grover量子搜索算法一经提出,其各种扩展算法也随之提出,其中最常用的一个为最小值查找量子算法。同样利用Grover迭代进行搜索,查找到最小值的时间复杂度同样为
次后,可以很高的概率得到目标解[16-17]。Grover量子搜索算法一经提出,其各种扩展算法也随之提出,其中最常用的一个为最小值查找量子算法。同样利用Grover迭代进行搜索,查找到最小值的时间复杂度同样为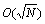 [18]。
[18]。
量子计数将Grover迭代和基于量子Fourier变换的相位估计技术相结合,能以比经典计算机快得多的方式求得解的数目[19]。Grover迭代G具有特征值为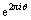 的特征向量
的特征向量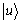 ,其中
,其中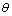 未知,相位估计算法可以利用量子Fourier技术估计
未知,相位估计算法可以利用量子Fourier技术估计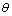 。估计的过程如下。
。估计的过程如下。
1) 输入初态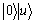 ;
;
2) 应用Hadamard变换后得到
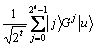
3) 应用受控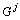 黑箱后得到
黑箱后得到
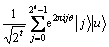
4) 应用逆Fourier变换得到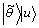
对第4)步结果中的第一寄存器进行测量便得到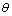 的估计值,然后进行相应的变换则能得到满足Grover迭代的解的个数[10]。
的估计值,然后进行相应的变换则能得到满足Grover迭代的解的个数[10]。
2 量子计算加速DDC算法
本节给出量子计算加速DDC算法的方案,即对每个数据点提出利用量子计数算法加速求解其局部密度,利用最小值查找量子算法加速求解其delta距离。
2.1 量子计数算法加速求解局部密度
局部密度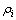 的求解过程实则为计数算法,即统计数据点
的求解过程实则为计数算法,即统计数据点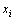 到其他各数据点的delta距离
到其他各数据点的delta距离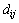 (j=0, …, N-1)中小于
(j=0, …, N-1)中小于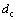 的个数。利用经典计数算法求解
的个数。利用经典计数算法求解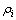 需要的时间复杂度为
需要的时间复杂度为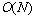 ,而量子计数算法完成同样的任务却能以比经典算法快得多的方式求得结果,故提出利用量子计数算法加速求解局部密度
,而量子计数算法完成同样的任务却能以比经典算法快得多的方式求得结果,故提出利用量子计数算法加速求解局部密度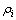 。
。
用量子计数算法求解局部密度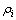 的量子线路图如图1所示。量子计数是对Grover迭代G特征值的相位
的量子线路图如图1所示。量子计数是对Grover迭代G特征值的相位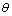 的估计过程。图1中第一寄存器包含t个量子比特,t由
的估计过程。图1中第一寄存器包含t个量子比特,t由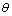 的估计位数以及相位估计过程中期望成功的概率决定,例如:若以至少
的估计位数以及相位估计过程中期望成功的概率决定,例如:若以至少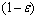 的概率估计
的概率估计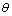 到m比特精度,则
到m比特精度,则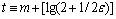 。第二寄存器包含n个量子比特,经过H门后,得到均匀叠加态
。第二寄存器包含n个量子比特,经过H门后,得到均匀叠加态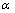 :
:
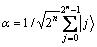
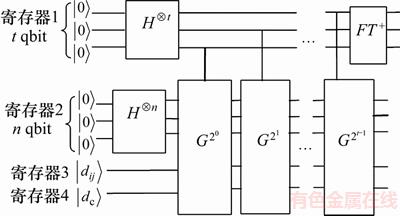
图1 求解局部密度的量子计数算法线路图
Fig. 1 Quantum circuit for solving local density
通常量子计数算法利用均匀叠加态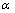 保存问题的解空间,但求解
保存问题的解空间,但求解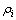 的解空间为
的解空间为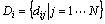 ,
,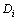 的各元素并不是和
的各元素并不是和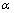 中的各量子态
中的各量子态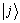 一一对应,且
一一对应,且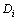 的元素可能有重复值的情况,例如:当
的元素可能有重复值的情况,例如:当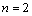 时,
时,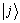 对应的量子态为
对应的量子态为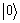 ,
,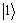 ,
,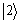 和
和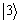 ,而
,而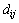 的取值可能为1,2,2和1,故
的取值可能为1,2,2和1,故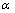 不能用于保存解空间
不能用于保存解空间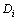 。鉴于此,另辟专门的内存区域用于保存解空间
。鉴于此,另辟专门的内存区域用于保存解空间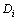 ,而
,而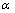 用于存放对
用于存放对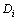 的内存索引,即当第二寄存器的状态为
的内存索引,即当第二寄存器的状态为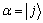 时,则
时,则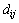 加载到第三寄存器中。由于量子计数主要是利用Grover迭代的量子黑箱Oracle实现,而Oracle工作在叠加状态下;为保证Oracle仍然工作在叠加情形,需要设计量子寻址方案,即实现第二寄存器
加载到第三寄存器中。由于量子计数主要是利用Grover迭代的量子黑箱Oracle实现,而Oracle工作在叠加状态下;为保证Oracle仍然工作在叠加情形,需要设计量子寻址方案,即实现第二寄存器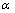 到内存区域的量子寻址。例如:1个具有4个内存单元的2 bit量子寻址方案设计如图2所示:当
到内存区域的量子寻址。例如:1个具有4个内存单元的2 bit量子寻址方案设计如图2所示:当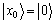 时,将量子比特接通到左侧,当
时,将量子比特接通到左侧,当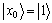 时,将量子比特接通到右侧,当
时,将量子比特接通到右侧,当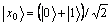 时,取2条路径的均匀叠加。图1中的第四寄存器保存
时,取2条路径的均匀叠加。图1中的第四寄存器保存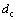 的值。
的值。
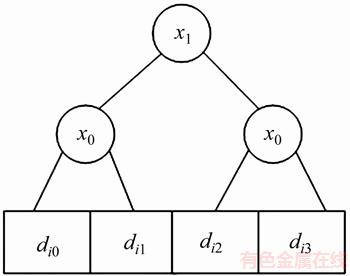
图2 两比特量子寻址方案
Fig. 2 Quantum addressing for 2 bit
利用量子计数求解局部密度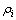 即是求解满足问题的解的数目,即满足式(1)的解的数目,解空间由Grover迭代进行搜索。Grover迭代主要是利用量子黑箱Oracle实现,用于求解
即是求解满足问题的解的数目,即满足式(1)的解的数目,解空间由Grover迭代进行搜索。Grover迭代主要是利用量子黑箱Oracle实现,用于求解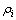 的量子黑箱定义为Oracle1,其定义如下:
的量子黑箱定义为Oracle1,其定义如下:
 (4)
(4)
由于Grover迭代可以看做是搜索问题的解与非解定义的二维空间的一个旋转,其旋转的角度为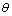 。在量子计数算法的最后一步,应用Fourier逆变换,并对第一寄存器进行测量后,可以得到
。在量子计数算法的最后一步,应用Fourier逆变换,并对第一寄存器进行测量后,可以得到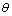 的估计值
的估计值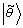 。最后利用下式即可求得解的数目
。最后利用下式即可求得解的数目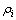 :
:
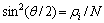 (5)
(5)
算法1:求解局部密度的量子计数算法
输入:1) 初始数据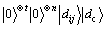 ;
;
2) 量子黑箱Oracle1。
输出:对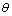 的m比特近似
的m比特近似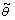 。
。
过程:
1) 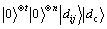 ;
;
2) 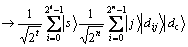 ;
;
3) 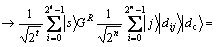
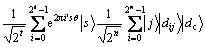
4) 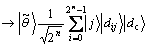 。
。
利用量子计数算法求解局部密度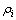 的过程详见算法1。
的过程详见算法1。
第1)步,输入初态。第2)步,应用H门到第一、第二寄存器。第3)步,进行Grover迭代,每经过1次迭代,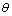 都会根据计数的情况有相应的变化。第4)步,对Grover迭代后的结果进行Fourier逆变换。对第4)步,输出结果的第一寄存器进行测量得到相位
都会根据计数的情况有相应的变化。第4)步,对Grover迭代后的结果进行Fourier逆变换。对第4)步,输出结果的第一寄存器进行测量得到相位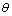 的估计值
的估计值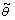 ,依据式(5)可以得出
,依据式(5)可以得出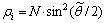 。
。
2.2 最小值查找量子算法加速求解delta距离
DDC算法求解delta距离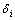 ,即求解比其局部密度
,即求解比其局部密度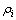 高的数据点中的距离最小值,该步骤实则为无序数据库求解最小值的过程,利用经典算法求解最小值的复杂度为
高的数据点中的距离最小值,该步骤实则为无序数据库求解最小值的过程,利用经典算法求解最小值的复杂度为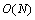 。最小值量子查找算法可以
。最小值量子查找算法可以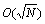 的时间复杂度查找最小值,故提出利用最小值查找量子算法求解delta距离
的时间复杂度查找最小值,故提出利用最小值查找量子算法求解delta距离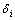 ,以期达到加速的目的。
,以期达到加速的目的。
利用最小值查找量子算法求解delta距离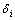 的量子线路图如图3所示。 共设置6个寄存器,寄存器1输入为初始为n比特的
的量子线路图如图3所示。 共设置6个寄存器,寄存器1输入为初始为n比特的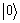 值,通过n个H门后生成均匀叠加态
值,通过n个H门后生成均匀叠加态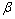 如下:
如下:
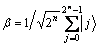
最小值查找量子算法通常利用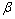 保存搜索问题的解空间;但是在DDC算法中,delta距离
保存搜索问题的解空间;但是在DDC算法中,delta距离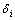 的解由其余各数据点的局部密度
的解由其余各数据点的局部密度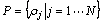 和delta距离
和delta距离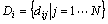 决定,且P和
决定,且P和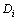 中的各元素值亦不与
中的各元素值亦不与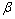 中的各量子态
中的各量子态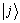 一一对应。为了充分利用解空间求得
一一对应。为了充分利用解空间求得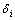 ,同样采取如2.1节中的方案,设置专门的内存区用于保存P和
,同样采取如2.1节中的方案,设置专门的内存区用于保存P和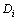 ,且
,且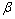 为其内存单元的索引,其量子寻址方案设计原理亦与2.1节中的相同。图3中第二至第五寄存器为n量子比特数据寄存器,其中第二寄存器用于保存
为其内存单元的索引,其量子寻址方案设计原理亦与2.1节中的相同。图3中第二至第五寄存器为n量子比特数据寄存器,其中第二寄存器用于保存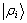 ;第四寄存器用于保存
;第四寄存器用于保存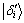 (
(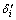 初始值为比较大的数);第三、第五寄存器初始值为
初始值为比较大的数);第三、第五寄存器初始值为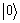 ,当内存索引寄存为
,当内存索引寄存为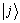 时,
时,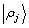 和
和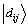 分别被加载到第三和第五寄存器中。第六寄存器保存Grover迭代的控制比特。
分别被加载到第三和第五寄存器中。第六寄存器保存Grover迭代的控制比特。
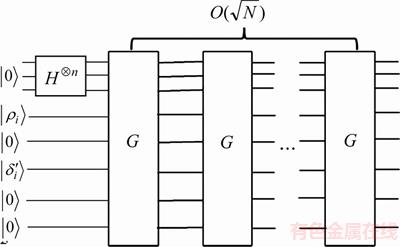
图3 求解delta距离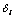 的最小值查找量子算法线路图
的最小值查找量子算法线路图
Fig. 3 Quantum circuit for solving delta distance
最小值查找量子算法搜索最小值的过程为Grover迭代,其Grover迭代实现的关键是量子黑箱Oracle的定义,用于求解delta距离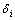 的量子黑箱定义为Oracle2,其实现的功能如下:
的量子黑箱定义为Oracle2,其实现的功能如下:
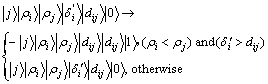 (6)
(6)
Oracle2的作用是如果同时满足条件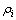 <
<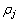 和
和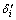 >
>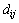 ,则控制比特进行翻转操作,同时将第四寄存器的值设置为
,则控制比特进行翻转操作,同时将第四寄存器的值设置为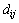 。
。
算法2:求解delta距离的最小值查找量子算法
输入:1) 初始数据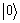
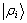
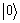
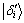
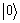 ;
;
2) 控制比特为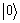 ;
;
3) 量子黑箱Oracle2。
输出:测量第四寄存器的值。
过程:
1) 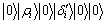 ;
;
2) 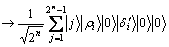 ;
;
3) 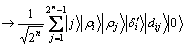 ;
;
4) if (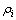 <
<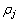 ) and (
) and (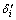 >
>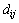 )
)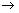

otherwise
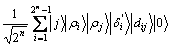 ;
;
5) 测量第四寄存器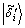 。
。
利用最小值查找量子算法求解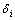 的过程见算法2。第1)步,输入初始数据。第2)步,应用H门到第一寄存器。第3)步,加载第
的过程见算法2。第1)步,输入初始数据。第2)步,应用H门到第一寄存器。第3)步,加载第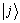 索引的内存单元数据分别到第三、五寄存器,同时标记(
索引的内存单元数据分别到第三、五寄存器,同时标记(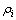 <
<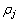 ) and (
) and (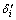 >
>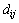 )的记录数t,该步时间复杂度为
)的记录数t,该步时间复杂度为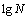 。第4)步,利用Grover迭代查找最小值,由于其最小值在满足(
。第4)步,利用Grover迭代查找最小值,由于其最小值在满足(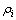 <
<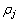 ) and (
) and (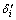 >
>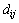 )的t条记录中,所以,该步最多需要
)的t条记录中,所以,该步最多需要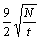 [18]。第5)步,对第四寄存器进行测量得到
[18]。第5)步,对第四寄存器进行测量得到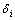 的估计值。
的估计值。
3 算法分析
3.1 量子计数算法加速求解局部密度的算法分析
量子计数算法是对Grover迭代G的相位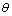 估计过程,计算的过程主要是Grover迭代。由于
估计过程,计算的过程主要是Grover迭代。由于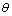 是以一定的成功概率估计到一定精度,则由
是以一定的成功概率估计到一定精度,则由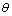 得到的局部密度
得到的局部密度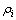 也是1个估计值,其与真实值之间存在一定误差
也是1个估计值,其与真实值之间存在一定误差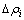 :
:
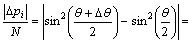
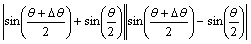 <
<
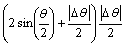 (7)
(7)
因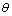 被估计到m比特精度,则
被估计到m比特精度,则
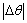 ≤
≤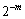 (8)
(8)
将式(5)与(8)代入式(7)可以得到
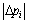 <
<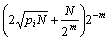 (9)
(9)
这里,取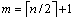 ,
,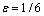 ,则
,则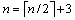 ,得到
,得到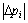 <
<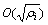 ,需要调用Oracle的次数为
,需要调用Oracle的次数为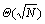 ,即其时间复杂度为
,即其时间复杂度为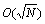 ,与经典算法
,与经典算法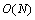 的时间复杂度相比较可以得到二次加速。
的时间复杂度相比较可以得到二次加速。
利用量子计数求解单个数据点局部密度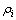 ,其时间复杂度可以从
,其时间复杂度可以从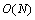 降到
降到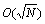 ,对于整个数据集,则时间复杂度可以从
,对于整个数据集,则时间复杂度可以从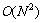 降到
降到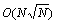 。
。
3.2 最小值查找量子算法加速求解delta距离的算法分析
文献[18]证明了给定数据规模为t的数据集,索引为r的记录被访问到的概率为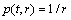 (r<t),而算法2的第1),2)和5)步为一步操作,所以,计算的过程集中在第3)和4)步,其需要的计算量为
(r<t),而算法2的第1),2)和5)步为一步操作,所以,计算的过程集中在第3)和4)步,其需要的计算量为
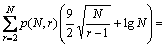
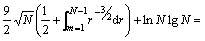
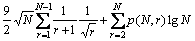 ≤
≤
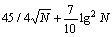
也即算法2能以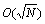 的时间复杂度求得每一个数据点的delta距离
的时间复杂度求得每一个数据点的delta距离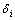 ,对于同样的任务,利用经典算法所需时间复杂度为
,对于同样的任务,利用经典算法所需时间复杂度为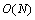 。对于规模为N的数据库,则求所有数据点的时间复杂度可以从
。对于规模为N的数据库,则求所有数据点的时间复杂度可以从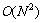 降到
降到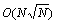 。
。
4 结论
1) 利用量子计算的相关算法对这一新颖的、可以自动识别簇数且数据分布自适应的DDC算法进行加速,对算法的2个主要参数即局部密度和delta距离的计算过程给出了量子计算的加速方案,利用量子计数算法加速求解局部密度,利用最小值查找量子算法加速求解delta距离。
2) 经过量子计算加速后,DDC算法的执行效率显著提升。
参考文献:
[1] JAIN A K, DUBES R C. Algorithms for clustering data[M]. New Jersey: Prentice-Hall, Englewood Cliffs, 1988: 45-46.
[2] XU Dongkuan, TIAN Yingjie. A comprehensive survey of clustering algorithms[J]. Annals of Data Science, 2015, 2(2): 165-193.
[3] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.
[4] CHENG Qing, LIU Zhong, HUANG Jincai, et al. Community detection in hypernetwork via Density-Ordered Tree partition[J]. Applied Mathematics and Computation, 2016, 276: 384-393.
[5] CHEN Yewang, LAI Dehe, QI Han, et al. A new method to estimate ages of facial image for large database[J]. Multimedia Tools and Applications, 2016, 75(5): 2877-2895.
[6] WANG Mengmeng, ZUO Wanli, WANG Ying. An improved density peaks-based clustering method for social circle discovery in social networks[J]. Neurocomputing, 2016, 179: 219-227.
[7] GHULIA P, SHUKLAA A, KIRANA R, et al. Multidimensional canopy clustering on iterative MapReduce framework using Elefig tool[J]. IETE Journal of Research 2015, 61(1): 14-21.
[8] 丁有伟, 秦小麟, 刘亮, 等. 一种异构集群中能量高效的大数据处理算法[J]. 计算机研究与发展, 2015, 52(2): 377-390.
DING Youwei, QIN Xiaolin, LIU Liang, et al. An energy efficient algorithm for big data processing in heterogeneous cluster[J]. Journal of Computer Research and Development, 2015, 52(2): 377-390.
[9] FORREST W. How to cut data centre carbon emissions 2008 [EB/OL]. [2014-12-08]. http//www.computerweekly.com/ Articles/ 2008/12/05/233748/how-tocut-data-centre carbon—emissions. htm.
[10] Nielsen M A, Chuang I L. Quantum computation and quantum information[M]. Cambridge, UK: Cambridge University Press, 2010: 221-263.
[11] ANGUITA D, RIDELLA S, RIVIECCIO F, et al. Quantum optimization for training support vector machines[J]. Neural Networks, 2003, 16(5): 763-770.
[12] REBENTROST P, MOHSENI M, LLOYD S. Quantum support vector machine for big data classification[J]. Physical review letters, 2014, 113(13): 130503.
[13] YOO S, BANG J, LEE C, et al. A quantum speedup in machine learning: finding an N-bit Boolean function for a classification[J]. 2014, 16(10): 103014-103028.
[14] LU S, BRAUNSTEIN S L. Quantum decision tree classifier[J]. Quantum information processing, 2014, 13(3): 757-770.
[15] 阮越, 陈汉武, 刘志昊, 等. 量子主成分分析算法[J]. 计算机学报, 2014, 37(3): 666-676.
RUAN Yue, CHEN Hanwu, LIU Zhihao, et al. Quantum principal component analysis algorithm[J]. Chinese Journal of Computers, 2014, 37(3): 666-676.
[16] GROVER L K. A fast quantum mechanical algorithm for database search[C]// Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. ACM. Philadelphia, Pennsylvania, USA, 1996: 212-219.
[17] BOYER M, BRASSARD G, H YER P, et al. Tight bounds on quantum searching[J]. Progress of Physics, 1998, 46(4/5): 493-505.
YER P, et al. Tight bounds on quantum searching[J]. Progress of Physics, 1998, 46(4/5): 493-505.
[18] DURR C, HOYER P. A quantum algorithm for finding the minimum[EB/OL]. [1999-01-07]. https://arxiv.org/pdf/quant- ph/9607014.pdf.
[19] BRASSARD G, HOYER P, TAPP A. Quantum counting[C]// International Colloquium on Automata, Languages, and Programming. Berlin Heidelberg: Springer, 1998: 820-831.
(编辑 杨幼平)
收稿日期:2017-07-04;修回日期:2017-09-17
基金项目(Foundation item):国家自然科学基金资助项目(61571226,61572053,61701229,61702367);江苏省自然科学基金资助项目(BK20170802,BK20140823) (Projects(61571226, 61572053, 61701229, 61702367) supported by the National Natural Science Foundation of China; Projects(BK20170802, BK20140823) supported by the National Science Foundation of Jiangsu Province, China)
通信作者:刘雪娟,博士研究生,从事量子计算、机器学习等研究;E mail: liu_juanjuan80@126.com
摘要:考虑到量子计算具有超强的并行计算能力,拟引入量子计算以降低局部密度和delta距离度量的聚类算法(DDC)计算复杂度。DDC算法的局部密度求解过程是计数算法,提出利用量子计数算法加速局部密度的求解;delta距离是最小值查找的过程,提出利用最小值查找量子算法加速delta距离的求解。研究结果表明:利用量子计算对DDC聚类算法进行加速,能够使算法的执行效率获得显著提升。


