Dynamic modeling of twin roll casting AZ41 magnesium alloy during hot compression processing
WANG Min(王 敏)1, WANG Shou-ren(王守仁)2, S. B. KANG3,J. H. CHO3, WANG Yan-jun(王砚军)2
1. School of Materials Science and Engineering, Shandong University, Ji’nan 250014, China;
2. School of Mechanical Engineering, University of Jinan, Ji’nan 250022, China;
3. Korea Institute of Materials Science, 66 Sangnam-dong, Changwon 641010, Korea
Received 23 September 2009; accepted 30 January 2010
Abstract:
A dynamic material model of Mg-4.51Al-1.19Zn-0.5Mn-0.5Ca (AZ41, mass fraction, %) magnesium alloy was put forward. The results show that the dynamic material model can characterize the deformation behavior and microstructure evolution and describe the relations among flow stress, strain, strain rates and deformation temperatures. Statistical analysis shows the validity of the proposed model. The model predicts that lower deformation temperature and higher strain rate cause the sharp strain hardening. Meanwhile, the flow stress curve turns into a steady state at high temperature and lower strain rate. The moderate temperature of 350 ℃ and strain rate of 0.01 s-1 are appropriate to this alloy.
Key words:
AZ41 alloy; flow stress; deformation behavior; dynamic model; twin-roll casting; hot compression;
1 Introduction
The inherently poor workability of magnesium alloys is the large obstacle in their engineering application. Owing to more workable at elevated temperatures because of the activation of non-basal slip systems such as prismatic áa? and pyramidal plane slip ác+a?, the studies about hot deformation behavior and microstructural evolution are necessary. So, many researchers have been dedicated to the dynamic material modeling (DMM) of Mg alloys at elevated temperatures[1-5]. LIU et al[6] put forward a new model of flow stress characterizing dynamic recrystallization of AZ31 as-cast magnesium alloy. TAKUDA et al[7] supposed a formula expressed in a simple form by means of the temperature-compensated strain rate. The famous mathematic model is power law which describes the strain hardening behavior of many alloys: 
, where 
is the strain rate, σ is the steady stress, n is the strain hardening exponent, Q is the activation energy, R is the gas constant and T is the deformed temperature. For creep, the power law is preferred. For hot-working materials, it is limited to relatively high deformed temperatures and low strain rates[8]. Whereas another equation, the exponential law
is suitable for hot deformation conditions of relatively low deformed temperatures and high strain rates[9]. There is a comprehensive and perfect equation, the sine hyperbolic law
which combines the power law and the exponential law. The description for the Zener-Hollomon parameter can be suitable for not only low and high deformed temperature but also the low and high strain rate regime. Despite a great deal previous publication describing DMM, however, little attention has been paid to the systematic study of associated twin-roll-cast (TRC) and hot compression (HC) processing of magnesium alloy. In this work, a detailed dynamic model was put forward to investigate the hot deformation behavior, microstructure evolution and deformation mechanism of AZ4.51-1.19Zn-0.5Mn-0.5Ca magnesium alloy by associated TRC-HC processing.
The AZ41 magnesium alloy used in this work has the chemical composition of Mg-4.51Al-1.19Zn-0.5Mn- 0.5Ca (mass fraction, %) of which optical micrograph is shown in Fig.1(a). The specimens were obtained by the
Fig.1 Optical micrographs of AZ41 alloy: (a) As cast; (b) As cast-strip; (c) Hot compression
twin-roll casting technique (TRC) and hot compression (HC). The microstructures of alloy after TRC and HC are shown in Figs.1(b) and (c), respectively. Firstly, a horizontal type twin roll caster with water-cooling system was used to manufacture AZ41 magnesium alloy strip. Pair of copper alloy rollers with 300 mm in diameter was used for the horizontal type twin roll caster. Molten alloy was heated to 720 ?C and then flowed down into the casting tundish. The molten metal contacted with cooled rollers and was rolled between the upper and lower rollers. The rolling speed was 5-6 r/min and the roller gap was 2 mm. A strip with 3.2 mm thick, 100 mm wide and 10 m long was manufactured. Secondly, late-form specimens with 50 mm long, 20 mm wide and 3 mm thick were machined from the strip for uniaxial compression tests which were carried out under isothermal conditions. HC tests were conducted at the temperatures of 573, 623 and 673 K and strain rates of 0.001, 0.01, 0.1 and 1.0 s-1, respectively. The specimens were quenched by nitrogen gas immediately after compression in order to prevent the microstructure from changing after deformation. Specimens for optical microstructural observation were cut from the strip along the plane formed by the rolling and normal direction and mechanically polished with polycrystalline diamond suspension glycol based solution. The grain structure was revealed by subsequent etching in 7 s with a solution of picric acid (5 g), acetic acid (5 mL), distilled water (10 mL), and ethanol (100 mL).
3 Results and discussion
3.1 True stress—true strain curve
The typical true stress—true strain plots obtained at the lower and higher temperatures of hot working range of Mg-4.51Al-1.19Zn-0.5Mn-0.5Ca alloy are shown in Fig.2. It is shown that the flow behavior of the materials is distinctly different at different temperatures and strain rates. It can be seen that the peak stress increases with the decreases of temperature and decrease with the decrease of strain rate. At the lower temperature (<573 K) and higher strain rates (>0.1 s-1), the materials exhibit severe strain hardening followed by failure occurred, thereby, the curve declines severely presenting load released. At the same time, at lower strain rate (<0.01 s-1), the materials exhibit the flow softening behavior followed by a steady decline towards a plateau. At the intermediate temperature (623 K), if the strain rates exceed 1.0 s-1, the materials still exhibit severe strain hardening and failure occur ultimately (Fig.2(b)). However, the flow stresses increase to a peak value and then decrease to a steady state under low strain rates (<0.1 s-1). At high temperature (673 K), the initial strain hardening components decrease and are inclined to steady state flow behavior at both lower and higher strain rate (Fig.2(c)). In conclusion, despite of the higher and lower strain rate and deformation temperature, the strain hardening mechanism plays a main role in hot working until the true strain exceeds the strain corresponding to the peak stress. Once the strain exceeds a critical value, the strain hardening will be restricted and flow softening mechanism takes up a dominant position.
3.2 Dynamic materials model
The relationship among true stress σ, true strain ε, strain rate and deformation temperature T can be described as
(1)
According to BASARAN and NIE[10], energy dissipations can be divided into two terms as intrinsic dissipation and thermal dissipation. The intrinsic
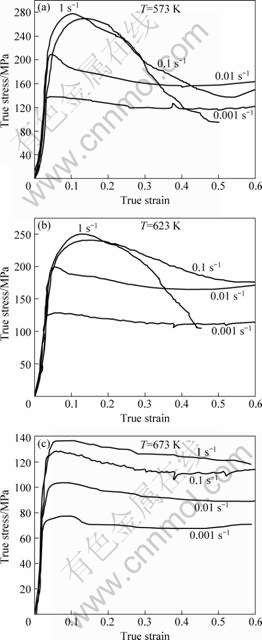
Fig.2 True strain—true stress curves obtained for AZ4.51- 0.5Mn-0.5Ca magnesium alloy by TRC-HC processing at different temperatures: (a) 573 K; (b) 623 K and (c) 673 K
dissipation consists of flow deformation and structural evolution dissipation. Then, it is possible to use the following statement:
(2)
where P is the total energy dissipation; G is the content dissipation related to kinetic energy and J is the co-content dissipation related to potential energy. The total energy dissipation can be divided by σ - curve where content G represents the area under the curve and co-content J represents the area above that curve shown in Fig.3(a). The content G and co-content J are related to a partitioning parameter, called the strain rate sensitivity (m):
(3)
If the flow softening mechanism taken up a dominant position holds a steady state, strain rate sensitivity falls into the range of 0＜m＜1. If no strain hardening occurs, the lower limit m=0 represents strain rate independent deformation for which no power is dissipated within the deformed material[11]. The upper limit m=1 means plastic deformation like a viscous fluid shown in Fig.3(b). So the co-content J can be denoted as
(4)
Eq.(4) is based on constitutive relation abided by the materials, 
where C is constant. When m=1, there is
(5)
The efficiency of power dissipation is defined as η=J/Jmax and can be calculated as
(6)
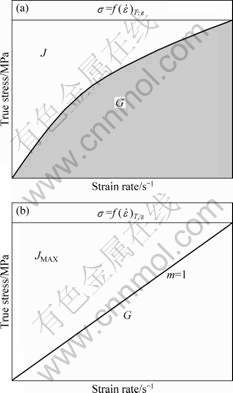
Fig.3 Schematic representation of constitutive relation of material system as energy dissipation: (a) Nonlinear energy dissipation; (b) Liner energy dissipation
where η is the non-dimensional efficiency index.
According to Arrhenuis equation, the Zener- Hollomon parameter is defined as[12]
(7)
where A and α are materials constants; n is stress exponent; R is the gas constant; Q is the activation energy; is the strain rate and T is the adiabatic deformation temperature. According to the linear relationship in ln—lnσ and ln—σ (Fig.4(a) and (b)), it can be calculated that the value of α=0.008 1 MPa-1. It is noted that σ value in Fig.4 is the stress corresponding to true strain of 0.5. Owing to the failure occurred in the higher strain rate (>1 s-1), ln—lnσ and ln—σ line deviate the corresponding peak stress value.
The logarithmic transformation for Eq.(7) is:
(8)
(9)
(10)
Then, n and Q can be expressed as
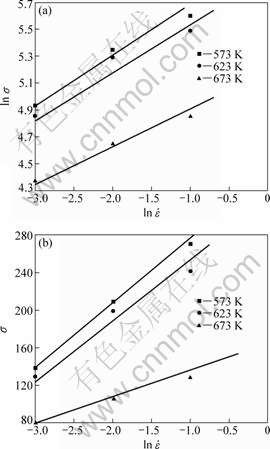
Fig.4 Relationship between strain and stress at different temperatures: (a) ln
as function of ln σ; (b) lnas function of σ
(11)
(12)
If Q and n are calculated, the flow stress equation is described as
(13)
(14)
3.3 Model constitution and verification
Eq.(9) demonstrates that there is a liner relation between 
and 
at different temperatures (Fig.5(a)) whose liner slope is 1/n. Eq.(10) demonstrates that the intercept of — line, A1(T), is linear related to 1/T. The liner slope of A1(T)—1/T is Q/nR and the intercept of that is -lnA/n (Fig.5(b)), so, n and Q can be calculated which are shown in Table 1 and the constant can also be calculated in an average as A=0.000 316.
Table 1 n and Q at different temperatures
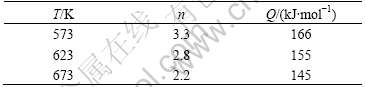
It is shown that stress exponent n increases with the decrease of temperature while activation energy increases with the increases of temperature. n falls into range from 2 to 12 referred by the Ref.[13]. Meanwhile, activation energy Q in the temperature range is larger than that for self-diffusion of pure magnesium which is 135 kJ/mol at 773-903 K. This is owing to the TRC-HC processing. So, the flow stress strain constitutive related model is constituted as
(15)
(16)
where n=2.2-3.3; Q=145-166 kJ/mol.
The peak stress (σP), steady stress (σS) and stress corresponding to strain 0.3 (σ0.3) at different strain rates and temperatures are shown in Fig.6. It is shown that peak stress is caused by superposition of hardening by dislocation storage and softening by dynamic recrystallization[12], and decreases with the increase of the deformation temperature at all strain rates (Fig.6(a)). There are high steady stresses at 623 K (Fig.6(b)). Meanwhile, it can be found that the steady stress value at 573 K and 0.1 s-1 appears an abnormal phenomenon which is lower than that of 573 K and 0.01 s-1 and 623 K and 0.1 s-1. This phenomenon also appears in Fig.6(c).
The model can be validated by statistics. Let and σ be two real-valued random variables over a common probability space. It is sometimes necessary to obtain information on the nature of the association (probabilistic relation) between and σ, beyond dependence or independence. A useful measure of statistical association between and σ is their correlation coefficient, defined by γ[14]:
(16)
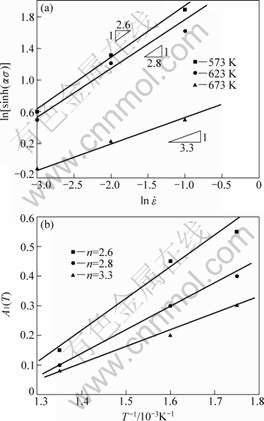
Fig.5 Linear relation of strain and stress at different temperatures: (a) 
—
and (b) A1(T)—1/T
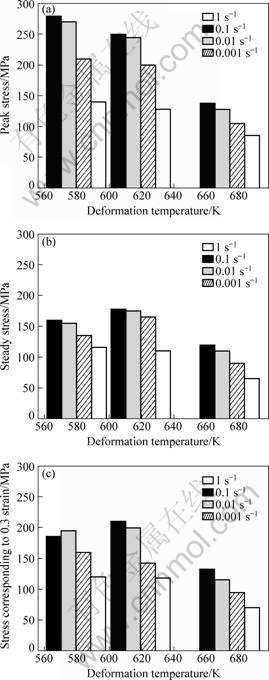
Fig.6 Stress variations of AZ4.51-0.5Mn-0.5Ca magnesium alloy by TRC-HC: (a) σP; (b) σS; (c) σ0.3
The correlation coefficient has the following properties as[15]: (I) -1≤γ≤1; (II) if |γ|=1, then and σ have a total correlation; (III) 0.3<|γ|<0.5, low correlation; and (IV) 0.5<|γ|<0.8, significant correlation.
When T=673 K, γ=0.699, which shows a significant correlation. It is indicated that the stress strain model is correct at high deformation. But when T=573 K, γ=0.356, which presents a low correlation showing that the relation between and σ cannot obey the power law relationship at high strain rate. This is just about the reason why the sample failures at strain rate of 1 s-1. The deviation between the model prediction values and the test values is about 3.25% according to statistical calculations.
1) A new model of flow stress under different deformation conditions (strain, strain rate and deformation temperature), characterizing the micro- structural evolution and DRX is put forward. It is validated by statistic and has been proved suitable for wide applications under intermediate deformation conditions of AZ41 alloy during TRC-HC processing.
2) The flow softening occurred at high temperature and low strain rate and the power-law behavior is followed. Nevertheless, the stress hardening behavior plays a main role at low temperature and high strain rate whilst the power law breaks down at this range.
AcknowledgementsAuthors thank Mr. S. S. JUNG and Mr. D. B. KIM for twin roll strip casting and Mr. E. S. WOO for hot compression test, who are working in Korea Institute of Materials Science.
References[1] MYSHLYAEV M M, McQUEEN H J, MWEMBELA A, KONOPLEVE E. Twinning, dynamic recovery and recrystallization in hot worked Mg-Al-Zn alloy [J]. Mater Sci Eng A, 2002, 337(1/2): 121-133.
[2] MWEMBELA A, KONOPLEVA E B, McQUEEN H J. Microstructural development in Mg alloy AZ31 during hot working [J]. Scripta Mater, 1997, 37(11): 1789-1795.
[3] SIVAKESAVAM O, RAO I S, PRADAD Y V R K. Processing map for hot working of as cast magnesium [J]. Mater Sci Technol, 1993, 9(9): 805-810.
[4] SRINIVASAN N, PRASAD Y V R K, RAMA RAO P. Hot deformation behavior of Mg-3Al alloy—A study using processing map [J]. Mater Sci Eng A, 2008, 476(1/2): 146-156.
[5] BEER A G, BARNETT M R. Influence of initial microstructure on the hot working flow stress of Mg-3Al-1Zn [J]. Mater Sci Eng A, 2006, 423(1/2): 292-299.
[6] LIU Juan, CUI Zhen-shan, LI Cong-xing. Modeling of flow stress characterizing dynamic recrystallization for magnesium alloy AZ31B [J]. Computational Materials Science, 2008, 41(3): 375-382.
[7] TAKUDA H, FUJIMOTO H, HATTA N. Modelling on flow stress of Mg-Al-Zn alloys at elevated temperatures [J]. J Mater Process Tech, 1998, 80/81: 513-516.
[8] SLOOFF F A, ZHOU J, DUSZCZYK J, KATGERMAN L. Constitutive analysis of wrought magnesium alloy Mg-Al4-Zn1 [J]. Scripta Materialia, 2007, 57(8): 759-762.
[9] MCQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Mat Sci Eng A, 2002, 322(1/2): 43-63.
[10] BASARAN C, NIE S. An irreversible thermodynamics theory for damage mechanics of solids [J]. Int J Damage Mech, 2004, 13(3): 205-223.
[11] POLETTI C, DEGISCHER H P, KREMMER S, MARKETZ W. Processing maps of Ti662 unreinforced and reinforced with TiC particles according to dynamic models [J]. Mater Sci Eng A, 2008, 486(1/2): 127-137.
[12] GALIYEV A, KAIBYSHEV R, GOTTSTEIN G. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60 [J]. Acta Mater, 2001, 49(7): 1199-1207.
[13] SONG S X, HORTON J A, KIM N J, NIEH T G. Deformation behavior of a twin-roll-cast Mg-6Zn-0.5Mn-0.3Cu-0.02Zr alloy at intermediate temperatures [J]. Scripta Materialia, 2007, 56(5): 393-395.
[14] ALTIOK T, MELAMED B. Simulation modeling and analysis with ARENA[M]. London: Academic Press,2007: 23-53.
[15] DUNN S M, CONSTANTINIDES A, MOGHE P V. Numerical methods in biomedical engineering [M]. London: Academic Press,2006: 345-388.
Foundation item: Project(Y2008F27) supported by the Natural Science Foundation of Shandong Province, China
Corresponding author: WANG Shou-ren, Tel: +86-531-82765476; Fax: +86-531-87108467; E-mail: sherman0158@tom.com
