J. Cent. South Univ. Technol. (2008) 15(s1): 302-306

DOI: 10.1007/s11771-008-368-1

Constitutive models in stability analysis of rock slope

YAN Zhi-xin(言志信)^{1, 2}, DUAN Jian(段 建)^{1, 2}, WANG Hou-yu(王后裕)³

(1. Key Laboratory of Mechanics on Disaster and Environment in Western China, Ministry of Education, Lanzhou University, Lanzhou 730000, China;

2. School of Civil Engineering and Mechanics, Lanzhou University, Lanzhou 730000, China;

3. Air Force Engineering Design and Research Bureau, Beijing 100077, China)

Key words:

equivalent Mohr-Coulomb yield criterion; constitutive model; rock slope; safety parameter；

1 Introduction

Rock slope has special mechanical properties owing to its unique structure and character of rock. It has almost all the mechanical properties that solid materials have, such as stickiness, elasticity, plasticity, nonhomogeneity, anisotropy, and so on, compared with other materials. This makes it difficult to get accurate answers in most rock projects^[1]. The deformation of rock mass not only varies from the level of load under the external load, but also is relevant to the stress of the loading. Besides the reversible elastic deformation, it can also have reversible plastic deformation^[2-3]. The researchers not only studied the constitutive models of rock materials but also got the calculating methods of stability safety parameters of rock slope without conspicuous slide surface and proved that it is liable to apply equivalent Mohr-Coulomb yield criterion to the measurable assessment of rock slope stability.

2 Equivalent Mohr-Coulomb yield criterion

2.1 Establishment of equivalent Mohr-Coulomb yield criterion

Since the yield surface of Mohr-Coulomb yield criterion is an informal hexahedron of a rhombohedron in main stress space, the surface’s angles are difficult to be calculated^[4]. Equal-surface area transform was made to Mohr-Coulomb yield criterion, that is to transform the angle-unequal, margin-equal hexagon on  plane into a circle whose area remains the same. Thus, a round cone yield surface is built up in main stress space and this makes the programming work easier. The round cone yield surface built in this way is called equivalent Mohr-Coulomb yield criterion. The criterion is a circle on  plane, which is also a Drucker-Prager(D-P yield criterion)^[5-6].

According to equivalent assumption, the concrete basic parameters of equivalent Mohr-Coulomb yield criterion are as follows:

Equivalent radius  is

                      (1)

Then

                        (2)

Equivalent cone rode angle  is:

(3)

where

Parameters  and k are

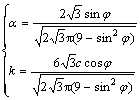                      (4)

2.2 Realization of equivalent Mohr-Coulomb yield criterion on Ansys

In order to use finite element software Ansys^[7-8] with equivalent Mohr-Coulomb yield criterion applied as the yield criterion of rock material at the same time, the transformation relationship needs to be built up among equivalent Mohr-Coulomb yield criterion and exterior angle points and circumscribed circles D-P yield criterion, and the later realizes the application of equivalent Mohr-Coulomb yield criterion on Ansys.

These two criteria (i.e., Equivalent Mohr-Coulomb yield criterion and exterior angle points and circumscribed circles D-P yield criterion) all act as a cone surface in vacuum and a circle on π surface with only difference in parameters  and k. However,  and k are functions relevant to material parameters c and . Therefore, taking the relationship among the criteria into account, the actual cohesion c and internal friction angle  of rock mass must transform into the material parameters  and  which are necessary to the analysis of Ansys, as Eqn.(6) shows.

Assuming that the actual cohesion c and internal friction angle  of rock mass are c and , the parameters needed in the analysis of Ansys under equivalent Mohr-Coulomb yield criterion are  and . According to the relationship among equivalent Mohr-Coulomb yield criterion and exterior angle points and circumscribed circles D-P yield criterion, there are:

         (5a)

         (5b)

The values of parameters needed in the analysis of Ansys  and  are:

   (6)

2.3 Comparison of parameters among equivalent Mohr-Coulomb yield criterion and exterior angle points and circumscribed circles D-P yield criterion

Assuming  is internal friction angle of rock mass, so its range is 0?≤≤90?, ∈[0, 1],

＜0,

so

＞9

According to Eqn.(6), there is

＜

＜

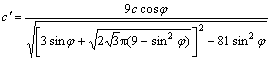With the analysis above, the parameters of rock become smaller compared with the original ones after transformation. According to the safety parameters principle of calculating slope safety parameter using finite element method intensity reducing method, the results calculated by equivalent Mohr-Coulomb yield criterion are constantly smaller than those using exterior angle points and circumscribed circles D-P yield criterion.

3 Safety parameters calculation of rock slope without conspicuous slide surface

Ansys is usually used to figure out relative safety parameter F of slide path regardless of its amount. Assuming that  is the maximum anti-slide force that the lower rock brings to resist the relative slide of the upper rock on slide path,  is the actual shearing force upon the lower stable rock which is put on by upper slide rock along slide path, namely descent slide force. Therefore, safety parameter F of rock slope is the ratio of  to . According to the structure network of rock, the slide path which is random in quantity is an irregular polygonal line pattern made up of polygonal line connected by a rock bridge and structure end to end. Thus, anti-slide force  is brought out by rock bridge, slide force  is brought out by structure surface. Therefore, the safety parameter F is:

                     (7)

where   and  are anti-slide forces and slide forces brought out by all rock bridges along slide path, respectively,  and   are anti-slide forces and slide forces brought out by all the structure surfaces along slide path, respectively.

3.1 Assurance of anti-slide force and slide force brought out by single rock bridge

Assuming that  is shearing angle,  is rock bridge incline angle,  is angle between horizontal direction and direction of principal stress producing tensile chap,  is angle between tensile chap and shearing direction, ,  and  derive from the data of stress field obtained by making finite element calculation. According to the theory of Lajtai and Einstein, when ＜, rock bridge will be damaged in the form of shearing failure; when ≥, rock bridge will be damaged in the form of tensile disruption. The formulas for calculating R_i and T_i under different forms of damage are shown as follows.

1) Shearing failure (＜)

            (8)

Where  c_i is the cohesion force of rock bridge,  is the normal stress put on rock bridge,  is the shear stress intensity of rock bridge,  is the shear force put on rock bridge.

    2) Tensile disruption (≥)

      (9)

where   is the tensile strength of rock,  is the tensile stress put on rock.

3.2 Assurance of anti-slide force and slide force brought out by single structure surface

It is simple to calculate R_j and T_j on structure. According to Mohr-Coulomb rule, there are:

            (10)

where   and  are the internal friction angle and cohesion force on structure surface, respectively; ,  and  derive from the data of stress field obtained by making finite element calculation; ,  and  are normal stress, shear stress intensity and shear stress put on structure surface, respectively; L is the length of structure surface.

4 Case analysis

4.1 Basic information

The height of a rock slope is H=60 m, slope angle β=70?. The physical parameters of rock slope and structure surface are shown in Table 1. Analyzing range is: 2 times of slope height in vertical direction, 4 times of slope height in horizontal direction, as shown in Fig.1.

4.2 Finite element analysis of rock slope

The marginal conditions of finite element model are as follows: land surface and slope surface are free boundary without confinement; the boundary of the model bottom is confined by the displacement in vertical direction; the horizontal boundary of the model is confined by horizontal displacement. Taking rock Plane42 element

Table 1 Material parameters used in calculation

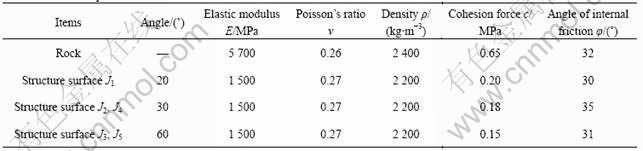
as its unit, and contact172 and targe169 to investigate structure surface, the model was divided into 590 units and 553 nodes, as shown in Fig.2. After finite element calculating in Ansys, normal stress on structure surface  and shear stress are shown in Figs.3-4.

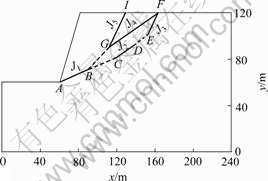
Fig.1 Slope section

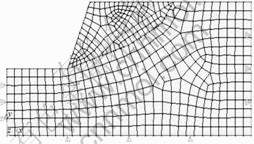
Fig.2 Finite element calculation model

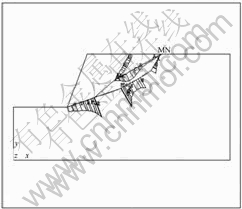
Fig.3 Normal stress on structure surface σ_n

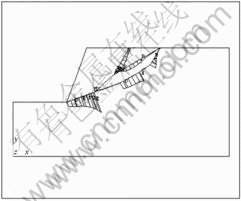
Fig.4 Shear stress on structure surface τ_s

4.3 Assurance of rock slope slide path

According to the searching principle of rock structure surface network and rock slope slide path, this rock slope case has 3 paths: A→B→C→D→E→F, A→B→G→F and A→B→G→I.

4.4 Assurance and validation of rock slope dangerous slide path

By analyzing the results of slope stress field in finite element method and using path tools in Ansys, with the judgment of damage upon rock bridge, through numerical integration of stress along the path of structure surface and rock bridge, anti-slide force, slide force and slide-resisted reserve are shown in Table 2.

With the data in Table 2, the results of different slide paths are shown in Table 3.

It can be seen form Table 3 that the safety parameter of path A→B→C→D→E→F(2.828) is the smallest one in these three paths, it is the dangerous slide path of this rock slope. The total slide-resisted reserve of path A→B→G→I(30 892 kN) is the smallest in these 3 paths. However, its relative safety parameter is 3.059. So it can be concluded that it is not the safest path. After analyzing the stability of rock slope with finite element intensity reducing method further, the safety parameter of this rock slope is 2.796, relatively close to the one of path A→B→C→D→E→F. So the algorithm presented by SHAN and CUI^[9], i.e. the path of which total slide-resisted reserve is the smallest is the dangerous slide path. It is inaccurate and needs to be amended.

Table 2 Results of rock bridge and structure surface

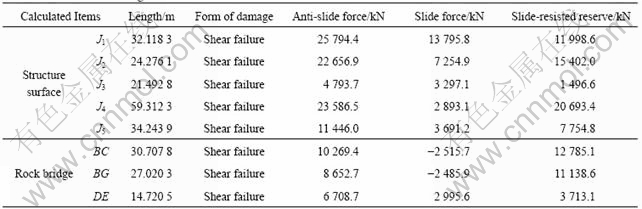
Table 3 Results contrast analysis of different paths

5 Conclusions

1) Equivalent Mohr-Coulomb yield criterion can be applied in the analysis of rock material elasticity and plasticity model and can also be applied using the giant finite element software Ansys. Meanwhile, the magnitude relationship of transformed material parameters and original ones is validated, that is, transformed parameters are constantly smaller than those of the original ones. Therefore, the results calculated by using equivalent Mohr-Coulomb yield criterion is constantly smaller than those calculated by using exterior angle points and circumscribed circles D-P yield criterion.

2) The results using finite element analysis can demonstrate the stress distribution of rock slope without conspicuous slide path along different paths reasonably and correctly and realize the accurate calculation of rock slope safety parameter.

3) Taking equivalent Mohr-Coulomb yield criterion into account, the safety parameter obtained by using finite element software Ansys is very close to that obtained by using finite element intensity reducing method.

4) The results obtained by the algorithm that selecting the path with the smallest total anti-slide force is inaccurate, it needs to be amended.

5) Although the safety parameter of rock slope without conspicuous slide path studied is larger than 1, the rock slope is constantly changeable, the parameter of rock slope becomes smaller and smaller, with the changeable speed becoming faster and faster in the last phase, finally, the safety parameter loses stability.

References

[1] LADE P V. Elasto-plastic stress-strain theory for cohesionless soil with curved yield surface[J]. Intern J Solids and Struct, 1977, 11(6): 1019-1035.

[2] ZHENG Ying-ren, SHEN Zhu-jiang, GONG Xiao-nan. The principle of geotechnical plastic mechanics[M]. Beijing: China Architecture and Building Press, 2003. (in Chinese)

[3] LADE P V. Modeoling yield surface for granular in three dimensions[J]. Computer Methods and Advances in Geomechanics, 1997, 25(4): 79-89.

[4] SUN D A, MATSUOKA H. An elastoplastic model for c+φ materials under complex loading[C]//9th Int Conf on Computer Methods and Advances in Geomechanics. Balkema, 1997.

[5] SHI Wei-min, ZHENG Ying-ren. The equivalent transform of Mohr-Coulomb yield criterion and its application in rock slope analysis[J]. Geotechnical Engineering Technique, 2003, 17(3): 155-159. (in Chinese)

[6] XU Gan-cheng, ZHENG Ying-ren. The study of yield criterion application in rock projects[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(2): 93-99. (in Chinese)

[7] LIU Tao, YANG Feng-peng, LI Gui-ming. Mastering ANSYS[M]. Beijing: Tsinghua University Press, 2001. (in Chinese)

[8] Bojia Science and Technology. Achieve mastery through a comprehensive study of finite element analysis soft-ANSYS[M]. Beijing: ChinaWater PowerPress, 2002. (in Chinese)

[9] SHAN Yan-jing, CUI Jun-zhi. Expectant slide route method of rock mass stability analysis in view of Statistical Model of structure surface and stress field[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(2): 151-157. (in Chinese)

(Edited by CHEN Can-hua)

Foundation item: Project(10672191) supported by National Natural Science Foundation of China; Project(06JJ50093) supported by Hunan Provincial Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: YAN Zhi-xin; Tel: +86-931-8632418; E-mail: yzx10@163.com