J. Cent. South Univ. Technol. (2009) 16: 0658-0662

DOI: 10.1007/s11771-009-0109-0

Strain rate effects on sand and its quantitative analysis

LI Fu-lin(李福林)^{1, 2}, PENG Fang-le(彭芳乐)^{1, 2}, LI Jian-zhong(李建中)³, KONGKITKUL W⁴

(1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China;

2. Key Laboratory of Geotechnical and Underground Engineering, Ministry of Education,

Tongji University, Shanghai 200092, China;

3. School of Geoscience and Environment Engineering, Central South University, Changsha 410083, China;

4. Department of Civil Engineering, King Mongkut’s University of Technology Thonburi, Bangkok 10140, Thailand)

Key words:

sand; strain rate; viscous properties; stress—strain relation；

1 Introduction

Viscous properties such as stain rate effects, creep, and relaxation play significant role in the behavior of soils. Strain rate effect is that stress—strain behaviors are affected by loading strain rate, that is, the curve of  stress—strain may change if loading strain rate changes. Most of the past experimental and theoretical studies of strain rate effects of soils have been focused on the characteristics of clayey soils [1-4]. On the other hand, the study on the strain rate effects of sand has been relatively limited [5-8]. Among these previous studies, all the considered sands exhibit significant viscous properties. However, the effects of loading method, wet condition and confining pressure on the viscous properties of sand have not been well studied and the viscous properties of sand has not been well quantified. To better understand the strain rate effects due to material viscous properties, a set of plane strain and triaxial compression tests on two clean sands (Hostun and Toyoura sands) were performed and a parameter β was introduced to characterize the observed viscous properties of sand in this work.

2 Experimental finding

2.1 Plane strain compression tests on Hostun sand

As can be seen in Fig.1, a series of drained plane strain compression (PSC) tests were performed at a constant confining pressure (i.e. the effective horizontal stress) of =392 kPa on saturated dense specimens of a clean sand (batch A of Hostun sand: a French sand with mean particle size D₅₀=0.31 mm, uniformity coefficient U_c=1.94, specific gravity G_s=2.65, and maximum/ minimum void ratio e_max/e_min=0.95/0.55) with precise stress and strain measurements [9-11]. The PSC specimens were rectangular prismatic with 20 cm in height, 16 cm in length and 8 cm in width (in the  direction). All the specimens were prepared by pluviating air-dried sand particles through air and were then made saturated during the respective plane strain compression test.

The specimens were first anisotropically consolidated at a stress ratio R=3.0 and a constant vertical strain rate = 0.012 5%/min, which means the basic axial strain rate, from the initial stress state with =29 kPa towards the final consolidation stress state with = 392 kPa. After that, the respective specimen was subjected

to drained PSC to the ultimate state. The initial void ratios e₀ of the specimens, measured at an isotropic stress state of =29 kPa, were nearly the same. As the cohesion of sand is equal to 0, stress ratio R is relevant to the internal friction angle representing the strength of sand. R =/=/, where  is the effective vertical stress;  and  are the effective major and minor principal stress, respectively. The following trend of behavior can be seen from these test results in Fig.1.

Fig.1 Relationship between R and γ from PSC tests on saturated Hostun sand

(1) From the tests H302C through H307C, the dense specimens were subjected to continuous monotonic loading (ML) at different vertical strain rates  by a factor of up to 500, and during each test  was kept constant. Noticeable strain rate effects can be seen only at the initial R and shear strain γ relationship immediately after the start of ML following anisotropic compression. γ=ε_v-ε_h=ε₁-ε₃, where ε_v and ε_h are the vertical and horizontal strains, respectively; ε₁ and ε₃ are the major and minor principal strains, respectively. The effects of strain rate on the overall stress—strain behavior are negligible.

(2) In another test HOS01, the axial strain rate was changed stepwise many times by a factor of 100 during otherwise ML at a constant axial strain rate. It may be seen in Fig.1 that the R increases with a very high stiffness, nearly elastic behavior, immediately after the strain rate is increased suddenly. Then, as long as ML continues at the changed strain rate, the stress—strain curve exhibits a marked change in the tangent modulus and gradually rejoins the essentially unique stress—strain curve obtained by continuous ML at any constant strain rate. The behavior opposite to the above takes place immediately after a stepwise decrease in the strain rate.

(3) It can also be seen from the test HOS01 that, the stress—strain curve exhibits a noticeable stress- overshooting immediately after the strain rate is increased stepwise during otherwise ML. On the other hand, a phenomenon of stress-undershooting takes place immediately after a step decrease in the strain rate during otherwise ML.

Nearly the same trends of behavior have been observed in PSC tests on air-dried Hostun sand and in triaxial compression (TC) tests on water-saturated and air-dried Toyoura sand as shown in the next section. Fig.2 shows the relationship between R and γ from another drained PSC test (Hsd02) on air-dried Hostun sand (batch B, e₀=0.700), in which  was changed stepwise several times by a factor of 100. The test conditions for this test (on air-dried Hostun sand) are essentially the same as those for test HOS01 (on saturated Hostun sand), of which the test results are presented in Fig.1. Fig.3 shows the result from a similar drained PSC

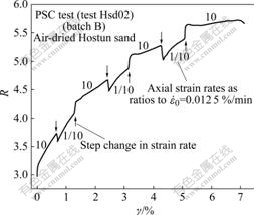
Fig.2 Relationship between R and γ from PSC test (Hsd02) on air-dried Hostun sand

Fig.3 Relationship between R and γ from PSC test (Hsd03) on air-dried Hostun sand

test (Hsd03) on air-dried Hostun sand (batch B, e₀= 0.698), in which the constant axial strain rate  was changed stepwise by a factor of 10 or 100 or 1 000.

2.2 Triaxial compression tests on Toyoura sand

The strain rate effects are observed not only on water-saturated and air-dried Hostun sand under plane strain conditions, but also on water-saturated and air-dried Toyoura sand under triaxial compression conditions. Figs.4 and 5 show the relationship between R and irreversible shear strain γ^ir=-, where  and  are the irreversible vertical and horizontal strains, from a pair of TC tests on the saturated (CC200r) and air-dried (DR200r) specimens, respectively. Rectangular prismatic specimens (18 cm in height and 11 cm×11 cm in cross-section) of Toyoura sand (a Japanese sand with D₅₀=0.21 mm, U_c=1.20, G_s=2.65, e_max=0.98 and e_min= 0.60) were prepared by the air-pluviation method. This specimen shape has been employed to use lateral local deformation transducers (LDTs) for sand previously [12-13]. To avoid an interaction with the lateral LDTs,

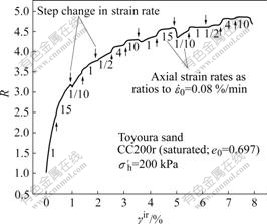
Fig.4 Relationship between R and γ^ir from TC test (CC200r) on saturated Toyoura sand

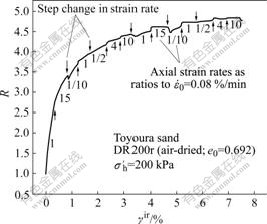
Fig.5 Relationship between R and γ^ir from TC test (DR200r) on air-dried Toyoura sand

the vertical LDTs were set on 7 mm-wide vertical belts that were made by trimming off the corners of the specimen.

The specimens were first isotropically compressed at a =0.002 5%/min from =30 kPa to =  200 kPa. Then, the specimens were performed by drained TC loading at a constant effective confining pressure.  was changed stepwise by a factor of between 2 and 150 during otherwise ML at a constant strain rate and = 0.08%/min. The irreversible strains were obtained by integrating their increments dε^ir=dε-dε^e. The elastic strain increment dε^e for a given stress increment was obtained based on a hypo-elastic model [14-15]. It can be found that the trends of strain rate effects observed in these two tests are essentially the same with those observed in the PSC tests on saturated and air-dried specimens of Hostun sand.

2.3 Summary

The observations discussed above can be summarized in Fig.6, and the very high initial stiffness immediately following the strain rate changed and the stress overshooting or undershooting phenomena can be found in all the concerned tests. As the strain rates were very small in all tests depicted in Figs.1-5, it is very likely that the specimens were always essentially under fully drained conditions, and therefore it is very unlikely that the viscous effects seen in Figs.1-5 are due to an interaction between the pore water and the sand skeleton and testing system. Furthermore, the effect of the inertia of the loading system on the measured stress values was utterly negligible when the strain rate was changed stepwise [10]. Therefore, the aforementioned strain rate effects should be attributed to the viscous properties of the tested sands.

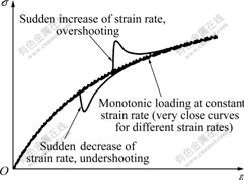
Fig.6 Schematic diagram of strain rate effects on sand

3 Quantitative analysis

The definition of stress jump DR upon a stepwise increase and decrease in the strain rate  is illustrated in Figs.7(a) and (b), respectively. It can be seen in Figs.1-5 that DR caused by each step change in  is essentially proportional to the instantaneous R, in which the step change in  was made. Subsequently, the following relationship is unique for these data obtained in the PSC tests.

                    (1)

where  and  are the irreversible vertical strain rates before and after a change in the strain rate, respectively; and the parameter β is the rate-sensitivity coefficient. For drained TC tests at a fixed confining pressure , Eqn.1 can be rewritten as follows:

                      (2)

where  and are the irreversible shear strain rates before and after a change in the strain rate, respectively.

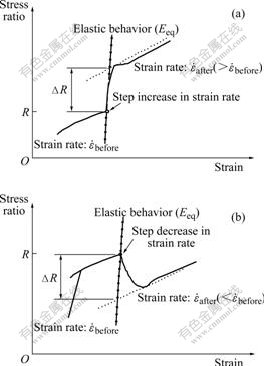
Fig.7 Definition of stress jump DR: (a) Step increase; (b) Step decrease

The stress ratios, DR/R, are plotted against the logarithm of the ratio of the irreversible strain rates after and before the respective step change, and , as shown in Figs.8 and 9 for the PSC tests (Hsd02 and Hsd03) and the TC tests (CC200r and DR200r), respectively. The following trends of behavior may be seen in Figs.8 and 9.

(1) DR/R is essentially independent of the value of R, which validates that the value of DR is always proportional to the instantaneous value of R.

(2) DR/R increases linearly in a broad sense as lg(/) increases. This fact means that the viscous stress component changes in a non-linear manner with the changes in the strain rate, unlike the Newtonian viscosity.

(3) β represents the characteristics of viscous property, which equals 0.021 3 and 0.024 2 for Hoston and Toyoura sands, respectively. It can be seen that β values obtained from PSC and TC tests are similar to each other, and the effects of the wet conditions and confining pressure are deemed to be negligible with sand.

Fig.8 Relationship between DR/R and ratio of irreversible strain rate from PSC tests (Hsd02 and Hsd03)

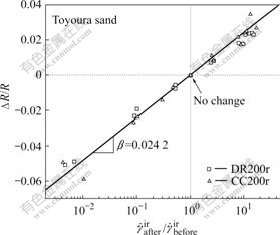
Fig.9 Relationship between DR/R and ratio of irreversible strain rate from TC tests (CC200r and DR200r)

4 Conclusions

(1) Significant strain rate effects due to material viscous properties, not due to delayed dissipation of excess pore water pressure, are observed with all the tested sands, including drained saturated and air-dried specimens of sand.

(2) The stress jump upon any stepwise changes in the strain rate decays with an increase in the irreversible strain when ML continues at a changed strain rate. The manner of stress decay observed in the TC tests is essentially the same as the one observed in the PSC tests.

(3) The viscosity of the tested sands can be represented by the rate-sensitivity coefficient β, which is essentially independent of loading method, wet condition and confining pressure under the considered conditions.

Acknowledgements

The authors would like to express their sincere thanks to Prof. TATSUOKA Fumio, Department of Civil Engineering, Tokyo University of Science, for his erudite guidance and discussions. The authors acknowledge gratefully the support provided by the Ministry of Education, Government, Science and Culture of Japan.

References

[1] SANTAGATA M, GERMAINE J T, LADD C C. Factors affecting the initial stiffness of cohesive soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(4): 430-441.

[2] XU Li-sheng, LI Jian-zhong. Viscous property of dried clay [J]. Journal of Central South University of Technology, 2006, 13(2): 204-207.

[3] DENG Jian-liang, TATSUOKA F, ZHANG Xiang-xia. Viscous effects on deformation of kaolin clay in drained 1D compression with cyclic loading [J]. Journal of Central South University of Technology, 2007, 14(S1): 405-408.

[4] LEONI M, KARSTUNEN M, VERMEER P A. Anisotropic creep model for soft soils [J]. Geotechnique, 2008, 58(3): 215-226.

[5] DIAZ-RODRIGUEZ J A, MARTINEZ-VASQUEZ J J, SANTAMARINA J C. Strain-rate effects in Mexico City soil [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(2): 300-305.

[6] LADE P V, LIU C T. Modelling creep behaviour of granular materials [C]// Proc 10th Int Conf on Comput Methods Adv Geomech. Tucson: Balkema, 2001: 277-284.

[7] AUGUSTESEN A, LIINGAARD M, LADE P V. Evaluation of time-dependent behaviour of soils [J]. International Journal of Geomechanics, 2004, 4(3): 137-156.

[8] WU P K, MATSUSHIMA K, TATSUOKA F. Effects of specimen size and some other factors on the strength and deformation of granular soil in direct shear tests [J]. Geotechnical Testing Journal, 2008, 31(1): 45-64.

[9] IBRAIM E, DI BENEDETTO H, DOANH T. Time-dependent behaviour and static liquefaction phenomenon of sand [J]. Geotechnical and Geological Engineering, 2009, 27(1): 181-191.

[10] MATSUSHITA M, TATSUOKA F, KOSEKI J, CAZACLIU B, DI BENEDETTO H, YASIN S J M. Time effects on the pre-peak deformation properties of sands [C]// Proc 2nd Int Conf on Pre-failure Deform Charact of Geomat. Torino: Balkema, 1999: 681-689.

[11] DI BENEDETTO H, TATSUOKA F, ISHIHARA M. Time-dependent shear deformation characteristics of sand and their constitutive modeling [J]. Soils and Foundations, 2002, 42(2): 1-22.

[12] TATSUOKA F. Inelastic deformation characteristics of geomaterial [C]// Proc Geotech Symp. Roma: Springer, 2006.

[13] HOQUE E, SATO T, TATSUOKA F. Performance evaluation of LDTs for the use in triaxial tests [J]. Geotechnical Testing Journal, 1997, 20(2): 149-167.

[14] NAWIR H, TATSUOKA F, KUWANO R. Experimental evaluation of the viscous properties of sand in shear [J]. Soils and Foundations, 2003, 43(6): 13-31.

[15] HOQUE E, TATSUOKA F. Anisotropy in the elastic deformation of materials [J]. Soils and Foundations, 1998, 38(1): 163-179.

(Edited by YANG You-ping)

Foundation item: Project(50679056) supported by the National Natural Science Foundation of China; Project(06-0378) supported by Program for New Century Excellent Talents in University; Project(05SG25) supported by the “Dawn” Program of Shanghai Education Commission, China; Project(B308) supported by the Shanghai Leading Academic Discipline, China

Received date: 2008-09-26; Accepted date: 2008-12-20

Corresponding author: PENG Fang-le, Professor, PhD; Tel: +86-21-65987532; E-mail: pengfangle@mail.tongji.edu.cn