中国有色金属学报

中国有色金属学报 2004,(04),534-538 DOI:10.19476/j.ysxb.1004.0609.2004.04.003

低铝含量Ni₇₅Al_xV_25-x合金早期沉淀过程的原子尺度计算机模拟

赵宇宏 陈铮 王永欣 唐丽英

西北工业大学材料科学与工程学院,西北工业大学材料科学与工程学院,西北工业大学材料科学与工程学院,西北工业大学材料科学与工程学院 西安710072 ,西安710072 ,西安710072 ,西安710072

摘 要：

采用微观相场模型,基于离散格点形式的微观扩散方程和非平衡自由能函数,编制了三元Ni75AlxV25-x合金的原子层面计算机模拟程序。模拟发现:低铝含量Ni75AlxV25-x合金的θ相先于γ′相析出,其沉淀机制为等成分有序化+失稳分解;γ′相在θ相的相界处非经典形核,二者均先形成非化学计量比有序相,之后向化学计量比有序相转变。

关键词：

早期沉淀;原子尺度;计算机模拟;

中图分类号： TG111

作者简介：赵宇宏(1974),女,博士.;

收稿日期：2003-03-25

基金：国家自然科学基金资助项目(50071046);

Atomic-scale computer simulation for early precipitation process of Ni₇₅Al_xV_75-x alloys with lower Al concentration

Abstract：

With the microscopic phase-field model, the atomic-scale computer simulation programs of the ternary Ni-based alloys were worked out based on the microscopic diffusion equation and nonequilibrium free energy. The results show that for Ni₇₅Al_xV_25-x alloy with lower Al composition, θ ordered phase precipitates earlier than γ′ ordered phase does by congruent ordering and spinodal decomposition mechanism, and thus produces a nonstoicheometric θ single ordered phase. Then, the nonstoicheometric γ′ phase precipitates by a non-classical nucleation and growth mechanism at the APBS of θ phases.

Keyword：

early precipitation process; atomic-scale; computer simulation;

Received： 2003-03-25

合金早期沉淀的时间尺度在秒级, 空间尺度在数十至数百原子, 即形成纳米级弥散强化相, 现有的实验手段研究合金沉淀早期的规律和机制非常困难, 采用原子层面的计算机模拟研究具有必要性, 并显示出实验手段无可比拟的优越性。 Pareige ^[1] 和Poduri ^[2] 等分别采用蒙特-卡洛法及相场法简单研究了Ni-Al-V合金的沉淀序列, 但均没有对合金沉淀早期的不同机制、 原子尺度的有序-无序转变及非平衡现象作深入探讨。

本文作者基于三元体系微观扩散方程, 通过对沉淀过程中原子图像、 序参数等的模拟和计算分析, 对低铝含量Ni-Al-V体系早期沉淀过程中γ′相(Ni₃Al)和θ相(Ni₃V)共存时有序相的析出序列及不同沉淀机制进行了研究。

1三元体系微观相场扩散方程

该模型首先由Khachatuyran ^[3] 提出, Chen等 ^[4,5,6,7] 做了发展。 设p_A(r, t), p_B(r, t), p_C(r, t)分别为A, B和C原子在t时刻占据格点位置r的几率, 由于p_A(r, t)+p_B(r, t)+p_C(r, t)=1, 所以每个格点上只有2个方程是独立的。 假设以A和B原子的占位几率为2个独立变量, 微扩散方程为

$\{\begin{array}{l}\frac{\text{d}p{}_{\text{A}}(r,t)}{\text{d}t}=\frac{1}{k{}_{\text{B}}{\rm T}}{\displaystyle \underset{r^{\prime }}{\sum }[L{}_{\text{A}\text{A}}(r-r^{\prime })\frac{?F}{?p{}_{\text{A}}(r^{\prime },t)}+}\\ L{}_{\text{A}\text{B}}(r-r^{\prime })\frac{?F}{?p{}_{\text{B}}(r^{\prime },t)}]\\ \frac{\text{d}p{}_{\text{B}}(r,t)}{\text{d}t}=\frac{1}{k{}_{\text{B}}{\rm T}}{\displaystyle \underset{r^{\prime }}{\sum }[L{}_{\text{B}\text{A}}(r-r^{\prime })\frac{?F}{?p{}_{\text{A}}(r^{\prime },t)}+}\\ L{}_{\text{B}\text{B}}(r-r^{\prime })\frac{?F}{?p{}_{\text{B}}(r^{\prime },t)}]\end{array}\text{?}\text{?}\text{?}(1)$

式中 L_αβ(r-r′)为与单位时间内1对α和β原子在格点位置r和r′上的交换几率有关的常数, α, β=A, B或C; F为体系的总自由能, 采用平均场自由能; T为温度; k_B为玻尔兹曼常数。

式(1)为确定方程, 不能描述形核过程, 需添加随机项来模拟热起伏, 使之变为随机方程, 并作傅立叶变换后, 得到傅立叶空间中的微观Langevin方程

$\{\begin{array}{l}\frac{\text{d}\stackrel{?}{{\displaystyle p}}{}_{\text{A}}(k,t)}{\text{d}t}=\frac{1}{k{}_{\text{B}}{\rm T}}{\displaystyle \underset{r^{\prime }}{\sum }［\stackrel{?}{{\displaystyle L}}{}_{\text{A}\text{A}}(k)\{\frac{?F}{?p{}_{\text{A}}(r^{\prime },t)}\}}{}_k+\\ \stackrel{?}{{\displaystyle L}}{}_{\text{A}\text{B}}(k)\left\{\frac{?F}{?p{}_{\text{B}}(r^{\prime },t)}\right\}{}_k]+\xi (k,t)\\ \frac{\text{d}\stackrel{?}{{\displaystyle p}}{}_{\text{B}}(k,t)}{\text{d}t}=\frac{1}{k{}_{\text{B}}{\rm T}}{\displaystyle \underset{r^{\prime }}{\sum }［\stackrel{?}{{\displaystyle L}}{}_{\text{B}\text{A}}(k)\{\frac{?F}{?p{}_{\text{A}}(r^{\prime },t)}\}}{}_k+\\ \stackrel{?}{{\displaystyle L}}{}_{\text{B}\text{B}}(k)\left\{\frac{?F}{?p{}_{\text{B}}(r^{\prime },t)}\right\}{}_k]+\xi (k,t)\end{array}\text{?}\text{?}\text{?}(2)$

式中 k为第一布里渊区定义的倒易格矢; $\stackrel{?}{{\displaystyle p}}{}_{\text{A}}(k,t)?\stackrel{?}{{\displaystyle p}}{}_{\text{B}}(k,t)?\stackrel{?}{{\displaystyle L}}{}_{\text{A}\text{A}}(k)?\stackrel{?}{{\displaystyle L}}{}_{\text{A}\text{B}}(k)?\stackrel{?}{{\displaystyle L}}{}_{\text{B}\text{A}}(k)?\stackrel{?}{{\displaystyle L}}{}_{\text{B}\text{B}}(k)?\xi (k,t)$ 为晶格位置坐标r有关函数的傅立叶变换。

用欧拉方法求解方程, 得到不同时刻的原子占位几率, 进而得到原子图像、 序参数分布等。

2模拟结果与分析

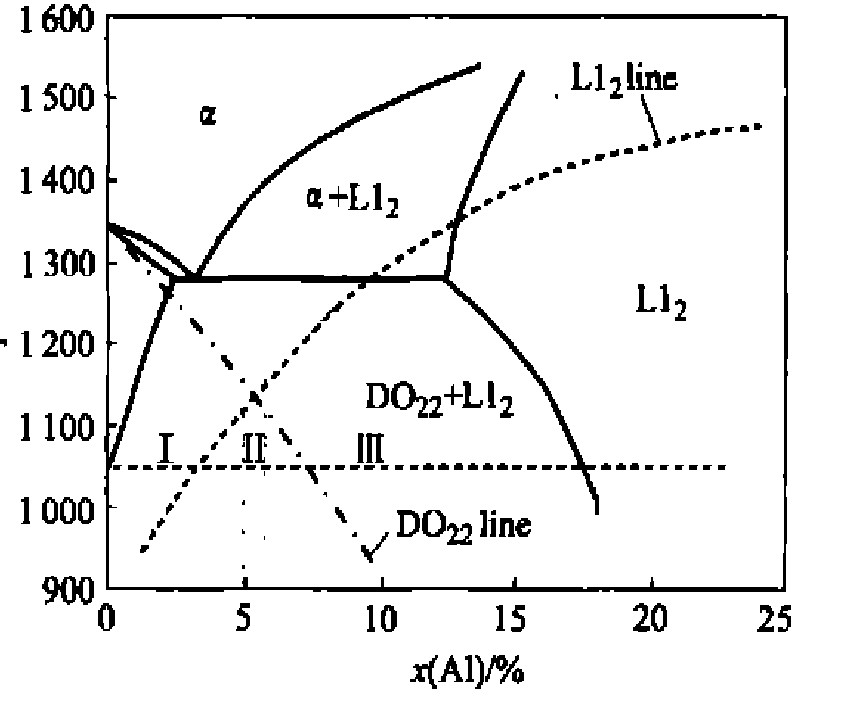
图1所示为由平均场理论计算的Ni₃Al-Ni₃V伪二元相图。 相图上粗实线为平衡相界线, 虚线“L1₂line”为L1₂相有序化失稳线, 其下方无序相因L1₂结构有序化而绝对失稳; 点划线“DO₂₂line”为DO₂₂相有序化失稳线, 其下方无序相因DO₂₂结构有序化而绝对失稳。 2条有序化失稳线交点对应的铝含量为5.3%。 本文将两相场区大致划分为3个区域: Ⅰ区低铝含量合金, 成分范围为0.8%～5.0%; Ⅱ区中间铝含量合金, 成分范围为5.0%～6.0%; Ⅲ区高铝含量合金, 成分范围为6.0%～1.7%。 本文选取位于Ⅰ区的Ni₇₅Al_3.2V_21.8合金为研究对象。

图1 由平均场理论计算的 Ni-Al-V伪二元Ni3Al-Ni3V相图

Fig.1 Computed pseudobinary Ni₃Al-Ni₃V phase diagram with mean field model

图2所示为不同时间步上该合金的模拟原子图像的演化,图3 和图4所示分别为该合金中θ相和γ′相晶核内部的成分序参数和长程序参数分布随时间的变化。

图2所示为铝含量为3.2%时, 不同时间步上合金的模拟原子图像演化过程,时间步长为0.000 2, 格点数为128×128, 镍, 铝和钒原子在每个格点上的占位几率值不同, 从而构成不同的有序结构。 图2(a)的时间步数为2 000, 此时合金仍处于无序基体状态。 图2(b)的时间步数为4 600, 无序基体开始发生有序化转变, 基体中出现一些DO₂₂有序结构。 图2(c)的时间步数为6 000, 合金中基本完全形成DO₂₂结构的θ有序畴及其90°旋转畴, 畴与畴之间被反相畴界(APBS)隔开, 铝原子在θ相界处聚集。 图2(d)的时间步数为15 000, 在有些APBS处开始出现另一种L1₂结构有序畴。 从图2(e)～2(f)中可观察到θ有序相的进一步粗化、 γ′相的继续长大及新的γ′相的形核。

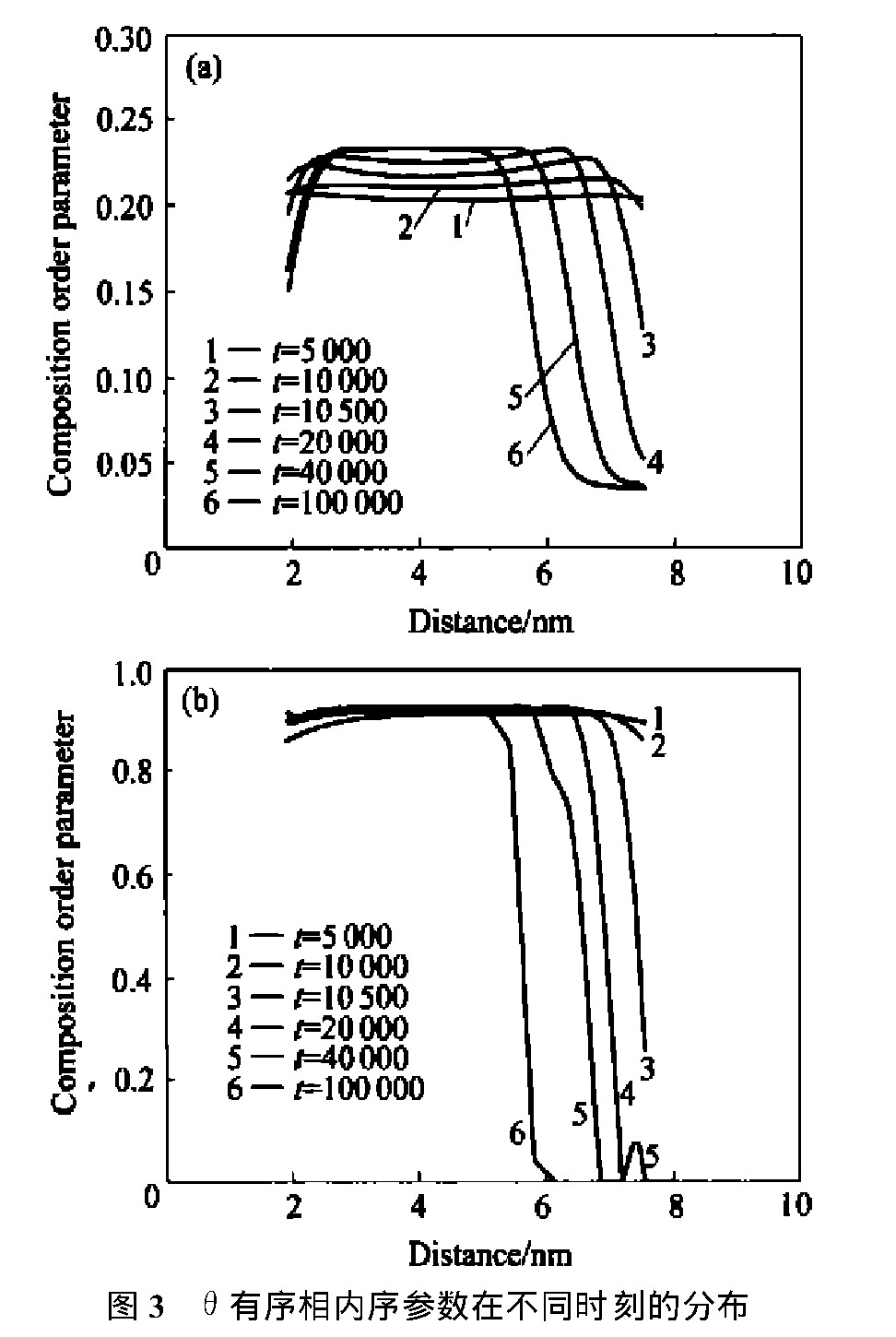
图3中, 在t=5 000时, 成分序参数分布很平, 没有起伏, 而同样时间步数上的长程序参数已经达到最大值, 此为典型的等成分有序化过程, 而且先形成的是非化学计量比θ有序相, 即成分低于平衡值而长程序参数已达平衡值。 接下来, 成分序参数发生范围甚大而程度较小的起伏, 并逐渐升至平衡值, 变为化学计量比θ有序相, 且具有明显的中间凹、 两头凸的特征, 是由于所选θ相左右两边相界处均有γ′相形核, 钒原子从θ相界向θ相内部扩散导致。 随着两边γ′相的逐渐长大, 此θ相变小, 反映在序参数变窄, 相内成分序参数分布逐渐变平, 说明钒原子已扩散至θ相中并达到平衡。

图2 铝含量为3.2%的合金在1 050 K时效时溶质原子占位几率随时间的演化Fig.2 Temporal evolution of occupation probabilities solute atoms at 1 050 K for alloy with 3.2%Al

(a)—t=2 000;(b)—t=4 600;(c)—t=6 000;(d)—t=15 000;(e)—t=20 000;(f)—t=100 000

图3 θ有序相内序参数在不同时刻的分布Fig.3 Order parameter profiles acrossθordered phase for alloy with 3.2%Al at different times

(a)—Composition order parameter;(b)—Long-range order parameter

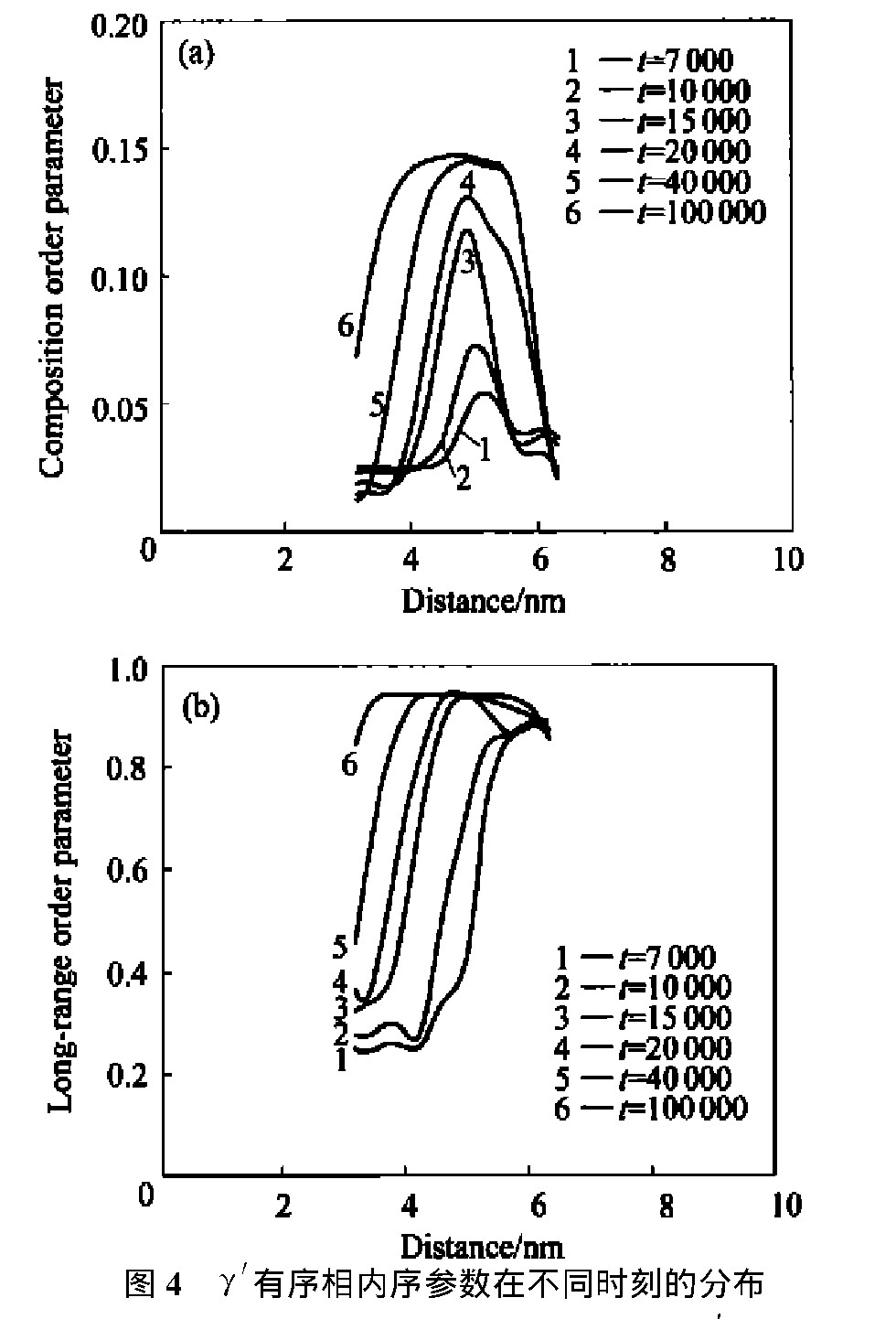
图4 γ′有序相内序参数在不同时刻的分布Fig.4 Order parameter profiles acrossγ′ordered phase for alloy with 3.2%Al at different times

(a)—Composition order parameter;(b)—Long-range order parameter

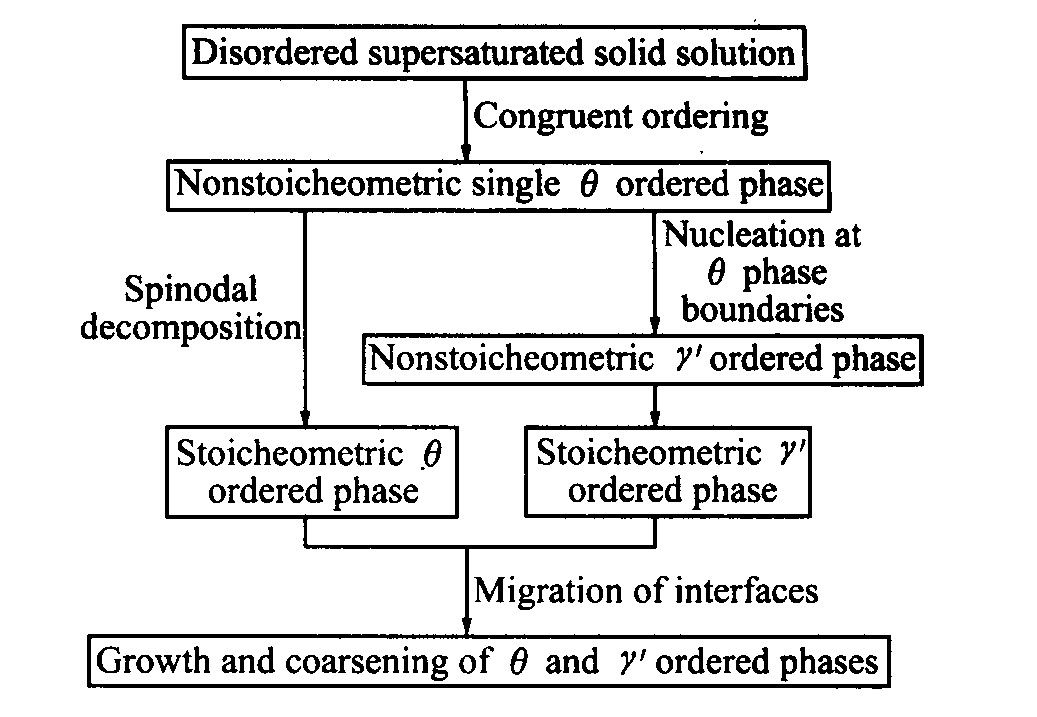
从图4可见, 该γ′有序相内成分序参数分布满足非经典形核的特点: 核心成分值较低, 远小于平衡值; 成分分布在相界面处有一定的空间延展尺度。 结合长程序参数, 认为先形成非化学计量比γ′相。 随着时效时间的延长, 核心成分值逐渐接近平衡, 转变为化学计量比γ′相。 Ni₇₅Al_3.2V_21.8合金的沉淀过程如图5所示。

3与相似实验的对照

美国宾夕法尼亚州大学Bendersky等 ^[8] 在对Ni₇₅Al_xV_25-x合金体系在1 073 K时效早期的实验观察中, 发现Ni₃Al和Ni₃V共存的组织形态, 认为Ni₃Al和Ni₃V构成伪二元系。 本文的模拟结果与其实验研究一致。

Zapolsky等 ^[9] 利用三维原子探针分析(3DAP)对三元Ni_78.5Al₇V_14.5体系在800 ℃等温时效时的转变路径进行了研究, 其研究发现, 沉淀过程中DO₂₂结构的θ相(Ni₃V)和L1₂结构的γ′相(Ni₃Al)同时析出。 图6所示为该研究提供的2种有序相的三维原子探针图。

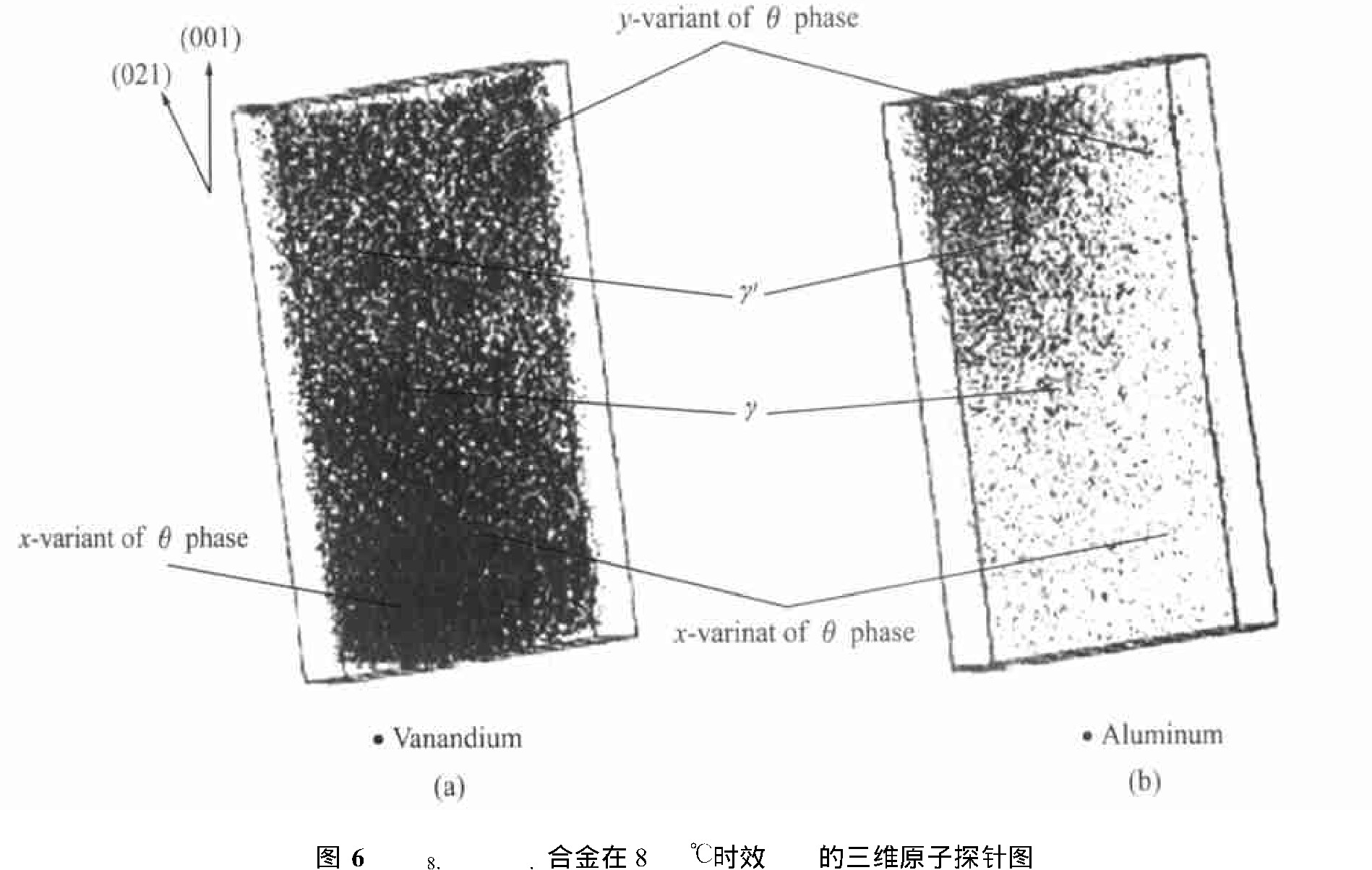
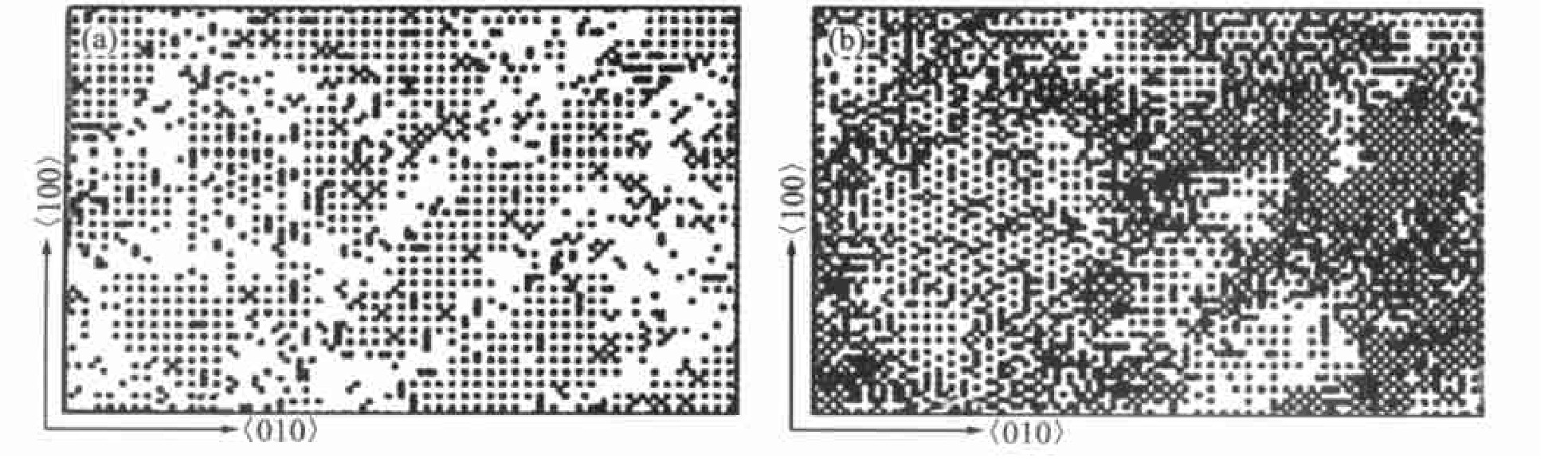
图7所示为Pareige采用蒙特卡洛方法对Ni_78.3Al_6.6V_15.1合金在800 ℃等温时效的早期过程进行研究 ^[1,2,6] 所得的三维原子图, 同样发现存在FCC→FCC+L1₂+DO₂₂动力学反应, 体系中θ相(Ni₃V)和γ′相(Ni₃Al)同时析出。

图5 Ni75Al3.2V21.8合金的沉淀过程

Fig.5 Precipitate process of Ni₇₅Al_3.2V_21.8 alloy

图6 Ni78.5Al7V14.5合金在800℃时效1 h的三维原子探针图Fig.6 3D atomic probe maps for Ni78.5Al7V14.5alloy aged at 800℃for 1 h

(a)—θphase;(b)—γ′phase

图7 Ni78.3Al6.6V15.1合金在800℃时效时的模拟图Fig.7 3D elemen tmaps of Ni78.3Al6.6V15.1alloy aged at 800℃with Monte-Carlo simulation

(a)—L1₂long ordered zones;(b)—DO₂₂long ordered zones

4结论

1) 低铝含量Ni₇₅Al_xV_25-x合金的无序相有序化动力学过程中有2种有序相沉淀析出, 分别是DO₂₂结构的θ有序相和L1₂结构的γ′有序相, 2种有序相构成伪二元体系。

2) 2种有序相的析出序列为: θ有序相先于γ′有序相析出。

3) 2种有序相的沉淀过程为: 原子的等成分有序化导致形成DO₂₂结构的单相θ有序畴, 畴与畴之间被反相畴界(APBS)隔开, 随后发生失稳分解, 铝原子开始在θ有序相的相上聚集, 同时钒原子从APBS上减少。 随着铝原子在相上聚集程度的增加, γ′有序相开始形核和长大。 所以θ相的沉淀机制为等成分有序化+失稳分解, γ′相的沉淀机制为异相非经典形核。

4) 两者均先形成非化学计量比有序相, 然后向化学计量比有序相转变。

参考文献

[1] 　PareigeC,BlavetteD.SimulationoftheFCC→FCC+L12+DO22kineticreaction[J].ScriptaMater,2001,44(2):243247.

[2] 　PoduriR,ChenLQ.Computer simulationofatomicorderingandcompositionalclusteringinthepseudobinaryNi3Al Ni3Vsystem[J].ActaMater,1998,46(5):17191729.

[3] 　KhachatuyranAG.TheoryofStructuralTransformationsinSolids[M].NewYork:Wiley,1983.139.

[4] 　MiyazakiT,KoyamaT,KozakaiT.Computersimulationofthephasetransformationinrealalloysystemsbasedonthephasefieldmethod[J].MaterSciEngA,2001,A312:3849.

[5] 　PoduriR,ChenLQ.Computersimulationofmorphologicalevolutionandcoarseningofδ′(Al3Li)precipitatesinAl Lialloys[J].ActaMater,1998,46(11):39153928.

[6] 　ChenLQ.Computersimulationofspinodaldecompositioninternarysystems[J].ActaMetallMater,1994,42(10):35033513.

[7] 　ChenLQ.Acomputersimulationtechniqueforspinodaldecompositionandorderinginternarysystems[J].ScriptaMetallurgicaetMaterialia,1993,29(5):683688.

[8] 　BenderskyLA.Solid SolidPhaseTransfomations[M].Warrendale,PA:TMS,1994.899902.

[9] 　ZapolskyH,PareigeC,MarteauL,etal.AtomprobeanalysesandnumericalcalculationofternaryphasediagraminNi Al Vsystem[J].Calphad,2001,25(1):125134.