
Finite element analysis of thermal residual stresses at cemented carbide rock drill buttons with cobalt-gradient structure
HUANG Zi-qian(黄自谦)1, HE Yue-hui(贺跃辉)1, CAI Hai-tao(蔡海涛)2,
XIAO Yi-feng(肖逸锋)1, HUANG Bai-yun(黄伯云)1
1. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;
2. School of Mathematical Sciences and Computing Technology, Central South University,Changsha 410083, China
Received 21 June 2007; accepted 12 November 2007
Abstract:
The aim of this study is to apply the concept of functionally graded materials(FGMs) to cemented carbides and to develop high-performance rock drill buttons. Cobalt-gradient structure was introduced to the surface zone of the buttons by carburizing process. Finite element method and XRD measurement were used to decide the distribution of thermal residual stress. Constitutive parameters were determined by constraint factor. Numerical results show that residual stresses of gradient buttons mainly concentrate in cobalt-gradient zone. There is compressive stress in the surface zone and tensile stress in the cobalt-rich zone. The maximum value of surface compressive stress is 180 MPa for WC-6Co cemented carbides. And the numerical results agree with the results of XRD measurement.
Key words:
cemented carbide; cobalt-gradient structure; finite element method; rock drill button; constraint factor;
1 Introduction
During machining application of cemented carbide tools, tensile stress occurs due to the thermal expansion difference arising from large temperature gradient. Thermal cracks easily develop and propagate to cause failure at work condition. According to the investigation of NOMURA et al[1], tool failure of cemented carbides was found mainly due to thermal cracking. Therefore, in order to develop high-performance tools, compressive residual stress should be introduced to material surface to prevent the occurrence of thermal cracking. This goal can be achieved by application of the concept of functionally graded materials(FGMs).
Between 1980s and 1990s, Sandvik introduced new materials that were described as “the most significant innovation in the history of cemented carbides” since the early 1950s[2-4]. The patented dual phase(DP) technology permits a simultaneous increase in both the wear resistance and toughness of cemented carbide, or either in property independently. The DP materials were achieved by changing the distribution of the cobalt within the insert, i.e. the formation of a cobalt-gradient structure. The DP grade cemented carbides showed an increase of 40% in service lifetime compared with conventional materials. Cobalt-gradient structure can be achieved by carburizing. The relationship among the morphology, content of η phase and the carbon content was studied[5-9]. The influence of the carburizing sintering temperature and carbon content on the formation of the gradient structure of the cemented carbide for mining was discussed, and the formation mechanism of gradient structure was analyzed. In this case, surface compressive stresses developed during cooling from processing temperature are good for service lifetime. But it is difficult to obtain the detailed data and distribution of residual stresses by experimental measurement.
Finite element method has a significant advantage to analyze the mechanism of residual stress formation. In 1973, TAMURA et al[10] proposed a concept of constraint factor q and the modified rule-of-mixtures. In 1993, WILLIAMSON et al[11-12] employed the modified rule-of-mixtures to simulate elastoplastic responses of FGMs. However, the graded region was discretized into strips of homogenous composition of the composites in WILLIAMSON’s model. It is time- consuming and less effective. Later GLANNAKOPOULOS et al used the modified rule-of- mixtures to determine the stress-strain parameters similarly[13], furthermore, the continuous functions of the spatial position were used to determine constitutive parameters instead of discretization of the graded region. It is the great progress of FGMs modeling.
In this study, carburization was used to form cobalt-gradient structure. The constitutive response for continuous and smooth variation of material properties is developed by constraint factor. XRD measurement was used to test the results of finite element calculation.
2 Experimental
The WC-6Co samples with total carbon content of 5.27%(mass fraction) were prepared by conventional powder metallurgy(PM) and carburized at 1 420-1 460 ℃ for different time in a pure H2 atmosphere. The morphology was analyzed by scanning electron microscopy(SEM) and the cobalt concentration gradient was analyzed by electron-probe microanalyses(EPMA). Fig.1 shows the three-layered structure of the cemented carbide after carburizing. In the backscattered- electron image, the outer layer and the inner layer are much brighter than the middle layer, in which a Co-rich region is formed. From Ref.[11], the microstructure of the presintered sample was mainly composed of WC, γ and η phase. η phase consisted of such complex carbides as Co2W4C, Co3W3C, and Co4W2C, and was formed only when the gross carbon content of the alloy was below the equilibrium level. On the surface, the microstructure was rich in WC, with η phase absent. The middle layer was rich in cobalt, also without η phase. The microstructure of the core alloy was almost the same as that of the as-presintered sample. Fig.2 shows the cobalt content distribution from the surface to the core. It can be seen that the cobalt content is around 3%(mass fraction) on the surface, then increases smoothly from the outer layer to the middle layer, suddenly cobalt content drops to the nominal content from the middle layer to the inner layer. The cobalt content is around 13% in the cobalt-rich zone and 6% in the core. Thus good wear resistance is obtained in the outer WC-rich zone and toughness of the alloy increases in the middle cobalt-rich zone.

Fig.1 Backscattered-electron image (BSE-SEM) showing graded structures of cemented carbide at 1 420 ℃ for 80 min
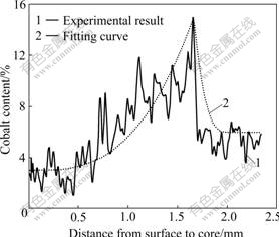
Fig.2 Cobalt content distribution from surface to core in substrate
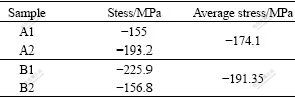
Thermal residual stresses of cemented carbides after carburizing were measured by XRD. For the same processing parameter, two samples were measured and the final results were average values. Samples were numbered A1, A2 and B1, B2, 60 min for A1, A2, and 120 min for B1, B2. Plane (103) of WC crystal was used to measure and the elastic modulus of WC was 534.4 GPa. Table 1 lists the measured results after carburizing. It can be seen from Table 1 that the surface compressive stress is 174.1 MPa for sample A and 191.35 MPa for sample B. The results show the surface macrostresses and the whole stress distribution could be achieved by finite element method.
Table 1 Surface residual stresses of cemented carbides by XRD
3 Numerical formulation and material model
As mentioned above, a model for continuous and smooth spatial variations in the composition and properties of materials was used. The model is available in the MSC. Marc2005 software.
We consider axisymmetric small strain problem of gradient buttons. The geometry model is given, as shown in Fig.3. The cobalt gradient is near the surface zone. The drill button is a cylinder with a hemisphere end.
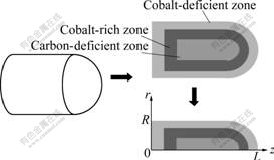
Fig.3 Finite element model of rock drill button
In the axisymmetric calculations, a cylindrical coordinate system (r, θ, z) is introduced and all field quantities are independent of θ. The dimension of buttons is 0≤r≤R ,0≤z≤L, and the ratio of L to R is 3/1. Free boundary condition is assumed.
The effective values of the thermal expansion coefficient, α, and Poisson’s ratio, ν, of the compositionally graded solid buttons were calculated by a volume fraction-based interpolation:
α=f1α1+f2α2, ν=f1ν1+f2ν2, f1+f2=1 (1)
where fi is the volume fraction of material i (0≤f1, f2≤1), and subscripts 1 and 2 refer to cobalt and tungsten carbide, respectively. Here, the isotropic properties of two phases are assumed. The approximate characteristics of the serial rule of mixture in Eqn.(1) is obvious. The effects of internal constraints at the level of the microstructure of the composite are not taken into account. Detailed knowledge of the microstructure is required if a more advanced rule of mixture is employed. Nevertheless, the present analyses provide first order results for the effect of compositional variations on the overall thermomechanical response to graded materials.
The stress—strain curves of composite were modeled using the intermediate law of mixture, as originally shown for cemented carbide by TAMURA et al[10] and later adopted for functionally graded materials(FGMs) by WILLIAMSON et al[11-13]. The gradient button is treated as an isotropic composite, for which the uniaxial stress σ and strain ε are related to the corresponding average uniaxial stress and strain of the two constituent phases as
σ=f1σ1+f2σ2, ε=f1ε1+f2ε2 (2)
And the elastic constraint factor (i.e., the ratio of strain transfer) p, is taken to be
p=ε1/ε2 (3)
If E1<E2, then 1≤p≤E2/E1 (4)
Obviously, p=1 and p=E2/E1, which correspond to properties of equal strain and equal stress, respectively. For Eqns.(2) and (3), effective elastic modulus E is derived explicitly as
![]() (5)
(5)
where Ei is the elastic modulus of material i. According to the test results, the value of p is taken as 3, which generally depends on the internal constraints arising from specific microstructural dispersion of the two phases, the thermomechanical properties and the residual stresses from processing.
Experimental measurements of elastoplastic deformation conducted on powder-metallurgy process show that when the composition, f1, of Co falls typically below 10%(mass fraction), the graded composite behaves essentially like an elastic solid. The experiment shows that there is no plastic deformation[14]. The cobalt content analyzed is less than 10%(mass fraction). Therefore, plastic deformation of WC-Co cemented carbide is ignored in this study. From the processing point of view, the above constitutive responses are approximations with respect to the constitutive volume fraction of the metal, f1, which in fact can be controlled through processing. The formulation is complete, once f1 is known as a function of the position.
According to experimental results of cobalt concentration, a function of the cobalt content distribution for the WC-Co graded alloys (i.e. the volume fraction f1 as a function of radial distance r) is constructed:
![]() (0≤r≤R) (6)
(0≤r≤R) (6)
where the constants m, n, k and l are correction factors; m represents the nominal cobalt content (mass fraction, %) in raw materials; n denotes the position of cobalt-rich zone with normalized unit; k is used to adjust the slope of cobalt gradient without unit and l to modify the least cobalt content (mass fraction, %) for avoiding the appearance of negative values of cobalt content. By varying the values of m, n, k and l, the different distributions of the cobalt content from the core to the surface zone are obtained. When m, n, k and l equal 6, 0.8, 0.015 and 0.035, respectively, the curve of cobalt content distribution is obtained (shown in Fig.4(a)). The corresponding distribution of elastic modulus and coefficient of thermal expansion is also shown in Fig.4. The majority of the simulation for gradient button model system incorporates the variation of mechanical properties with temperature, as listed in Table 2[14].
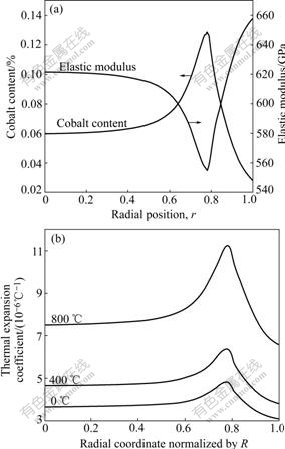
Fig.4 Curves of material property: (a) Cobalt content and elastic modulus; (b) Coefficient of thermal expansion at different temperatures
Table 2 Temperature-dependence of thermomechanical properties of WC(α1, α2) and γ-Co[14]
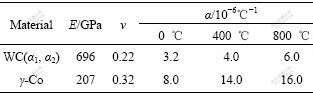
4 Numerical results
In this study, macrostresses of gradient buttons derived from cobalt gradient were considered. Free boundary condition and uniform cooling were assumed. The cobalt concentration difference in the cobalt gradient zone is about 0.1. Fig.5 shows the distribution of equivalent Von Mises stress after the temperature drops from initial stress-free temperature of 800 ℃ to 0 ℃. From Fig.5, it can be found that thermal equivalent stress mainly concentrates in cobalt-gradient zone and in the core, and the stresses are quite small. There are two peak zones of stress in the cobalt-rich zone and the surface zone. High stress concentration occurs in cobalt-gradient zone. There is a pile-up of tensile stress in the cobalt- rich zone and a compressive stress pile-up in the surface zone (shown in Fig.6). A neutral stress plane exists between the cobalt-rich zone and the surface zone. The maximum value of surface compressive stress is around 180 MPa and the maximum value of tensile stress in cobalt-rich zone is around 252 MPa. Table 1 shows that the surface compressive stress is 174.1 MPa for sample A and 191.35 MPa for sample B. Here, the sample used for finite element model was carburized for 80 min. The value of 180 MPa is between the measured results and just agrees with the experimental results. Strain distribution has similar characteristics of stress distribution. Material deformation mainly concentrates in cobalt gradient zone (shown in Fig.7). There is a little elastic deformation in the core. In the bottom margin of drill buttons, strain values are smaller than those of the counterparts with the same thickness.
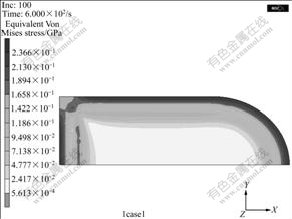
Fig.5 Contour plot of equivalent Von Mises stress after temperature dropping from initial stress-free temperature of 800 ℃ to 0 ℃
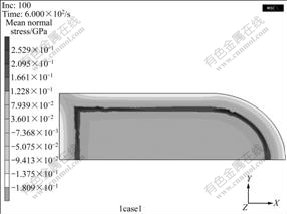
Fig.6 Contour plot of mean normal stress
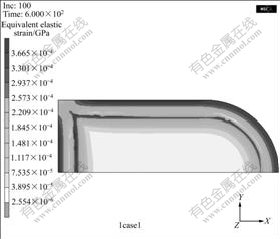
Fig.7 Contour plot of equivalent of elastic strain after temperature dropping from initial stress-free temperature of 800 ℃ to 0 ℃
According to NOMURA’s investigation[1], the compressive stress value should be 500-700 MPa in order to prevent the occurrence of thermal cracks. Thus, the cobalt content difference should be increased to obtain more large compressive stress on the surface. The numerical results show that the difference of cobalt concentration should be above 15%(mass fraction) so as to get enough compressive stress values. In order to get enough cobalt concentration difference, the initial cobalt content in the compact should increase to about 10%(mass fraction).
5 Conclusions
1) Cobalt-gradient structure is formed near the surface by carburizing. Compressive residual stress is introduced to prevent thermal cracking of gradient buttons by grading the composition. XRD measurement shows that the surface compressive stress is 174.1 MPa for 60 min-carburized sample and 191.35 MPa for 120 min-carburized one.
2) According to finite element calculation, thermal residual stresses of gradient buttons mainly concentrate in cobalt gradient zone. There is compressive stress in the surface zone and tensile stress in the cobalt-rich zone. The maximum value of surface compressive stress is around 180 MPa and the maximum value of tensile hydrostatic stress in cobalt-rich zone is around 252 MPa. Numerical results agree with the results of XRD measurement.
3) The difference of cobalt concentration should be above 15% so as to get the enough compressive stress values on the surface. So the initial cobalt content in the compact should be increased to about 10%.
References
[1] NOMURA T, MORIGUCHI H, TSUDA K, ISOBE K, IKEGAYA A, MORIYAMA K. Material design method for the functionally graded cemented carbide tool [J]. Int J Refract Met H, 1999, 17: 397-404.
[2] FISCHER U K R, HARTZELL E T, AKERMAN J G H. Cemented carbide body used preferably for rock drilling and mineral cutting [P]. US 4743515, 1998-05-10.
[3] AKERMAN J G H, FISCHER U K R, HARTZELL E T. Cemented carbide body with extra tough behavior [P]. US 5279901, 1994-01-18.
[4] FISCHER U K R, HARTZELL E T, AKERMAN J G H. Cemented carbide body with a binder phase gradient and method of make the same [P]. US 4820482, 1989-04-11.
[5] LIU Yong, WANG Hai-bin, YANG Jian-gao. Formation mechanism of cobalt-gradient structure in WC-Co hard alloy [J]. Journal of Materials Science, 2004, 39: 4397-4399.
[6] YANG Jian-gao, WANG Hai-bing, LIU Yong, ZHANG Lin-qiu, LI Fang, LONG Zheng-yi. Influence of carbon content on formation of gradient structure of cemented carbide for mining [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(3): 424-428. (in Chinese)
[7] ZHANG Li, CHEN Shu, XIONG Xiang-jun, HUANG Bai-yun, ZHANG Chuan-fu. Microstructure and Vickers hardness of functionally graded WC-Co cemented carbide with dual phase structure [J]. The Chinese Journal of Nonferrous Metals, 2005, 15(8): 1194-1199. (in Chinese)
[8] ZHANG Wu-zhuang, LIU Yong, HE Yue-hui, YANG Jian-gao, LONG Zheng-yi. Coated cemented carbide with gradient structure [J]. The Chinese Journal of Nonferrous Metals, 2005, 15(5): 757-762. (in Chinese)
[9] TAN Xing-long, QIU Shao-yu, HE Wen-yan, LEI Dai-fu, REN Da-peng. WC/ Co nano hardmetal materials made by spark plasma sintering technology [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(s1): 276-279.
[10] TAMURA I, TOMOTA Y, OZURA M. Strength and ductility of Fe-Ni-C alloys composed of austenite and martensite with various strength [C]// Proc Third Int Conf Strength of Metals and Alloys. London: Institute of Metals, 1973: 611-615.
[11] WILLIAMSON R L, RABIN B H, DRAKE J T. Finite element analysis of thermal residual stresses at graded ceramic-metal interfaces (Part I): Model description and geometrical effects [J]. J Appl Phys, 1993, 74: 1310-1320.
[12] WILLIAMSON R L, RABIN B H, DRAKE J T. Finite element analysis of thermal residual stresses at graded ceramic-metal interfaces (Part II): Interface optimization for residual stress reduction [J]. J Appl Phys, 1993, 74: 1321-1326.
[13] GLANNAKOPOULOS A E, SURESH S, FINOT M, OLSSON M. Elastoplastic analysis of thermal cycling: Layered materials with compositional gradients [J]. Acta Metal Mater, 1995, 43: 1335-1354.
[14] KIEFFER R, SCHWARZKOPF P. Hardmetals [M]. WANG Shao-gang, transl. Beijing: China Industry Press, 1963: 337, 359.
Foundation item: Project(50323008) supported by the National Natural Science Foundation of China
Corresponding author: HE Yue-hui; Tel: +86-731-8877391; E-mail: yuehui@mail.csu.edu.cn


