J. Cent. South Univ. Technol. (2011) 18: 140-145

DOI: 10.1007/s11771-011-0671-0

Linearization of T-S fuzzy systems and robust H∞ control

YOON Tae-Sung, WANG Fa-guang(王法广), PARK Seung-Kyu, KWAK Gun-Pyong, AHN Ho-Kyun

School of Mechatronics, Changwon National University, Changwon 641-773, Korea

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Key words:

T-S fuzzy control; linearization; H∞ control; sliding mode control；

1 Introduction

T-S fuzzy model is widely applied in many works [1-4]. A T-S fuzzy controller is described by using a set of local linear controllers. A global controller is constructed from the local controllers in such a way that global stability with various performance indexes of the closed-loop fuzzy control system is guaranteed. The major techniques that have been used include quadratic stabilization, linear matrix inequalities (LMIs), Lyapunov stability theory, bilinear matrix inequalities and so on [5-8]. Definitely, T-S fuzzy model provides a basis for the development of systematic approaches to stability analysis and controller design of fuzzy control systems in view of powerful conventional control theory and techniques. However, the requirement of stability condition is conservative for the designing of a T-S fuzzy controller. So, a great deal of attention is focused on the stability analysis of T-S fuzzy system. The requirement of stability conditions and their conservatism make it difficult to use the linear conventional control techniques for the T-S fuzzy model. These difficulties are more severe in the case of the existence of uncertainties and time delay in the T-S fuzzy system [9-12]. These difficulties are not shown in control of linear systems. Once the T-S fuzzy model has been linearized, the conventional linear controllers can be used without such difficulties. Therefore, the purpose of this work is to linearize T-S fuzzy model and makes direct use of linear control theories possible. To the best of our knowledge, there is less linearization technique applicable for T-S fuzzy model. The conventional linearization methods cannot be used for T-S fuzzy model because fuzzy rules and membership functions are included in the T-S fuzzy model. So, a new linearization technique for T-S fuzzy model by using T-S fuzzy state transformation is proposed. A T-S fuzzy model was transformed into linearizable form and then fuzzy feedback changed it into a linear controllable canonical form. The linearizable condition of the proposed linearization technique is just the controllability of linear local models which is easy to be checked and guaranteed. In the conventional linearization techniques, checking the size of the class of linearizable systems has been considered as an open problem [13-15]. Therefore, the result of this work can be considered as a new approximate linearization which has easier linearizable conditions for nonlinear systems. In this work, the T-S fuzzy system with uncertainties is also considered.

The SMC and optimal control were applied for the linearized T-S fuzzy system. The SMC input pushed the state onto the predetermined sliding surface and states could have the desirable dynamics of the surface in spite of uncertainties. Therefore, the system could be robust to parameter uncertainties and disturbances [16-19]. In this work, a robust H_∞ controller was designed for T-S fuzzy model by using the proposed linearization and SMC.

2 Problem formulation

The T-S fuzzy model was proposed by TAKAGI and SUGENO [5] to represent the local linear dynamic relations of nonlinear systems. The local linear models are described by fuzzy If-Then rules and can be employed to deal with the control design problem of nonlinear systems. The i-th rule of the fuzzy model is of the following form:

Plant Rule i:

If λ₁(t) is F_il, …, and λ_g(t) is F_ig

Then                 (1)

for i=1, 2, …, L, where F_ig is the fuzzy set,   L is the number of If-Then rules, and λ₁(t), λ₂(t), …, λ_g(t) are premise variables.

By using a standard fuzzy inference method, that is, using a singleton fuzzifier, product fuzzy inference, and center-average defuzzifier, the T-S fuzzy model in Eq.(1) can be rewritten as

               (2)

where λ(t)=[λ₁(t), λ₂(t), …, λ_g(t)], F_ij(w(t)) is the grade of membership of λ_j(t) in F_ij and

                        (3)

In this work, it is assumed that μ_i(λ(t))≥0 for i=1,

2, …, L and  for all t. Therefore, h_i(λ(t))≥ 0 was obtained for i=1, 2, …, L and

                               (4)

Classical T-S controller has the following form:

                        (5)

Overall, T-S fuzzy system is written as

     (6)

Each local linear controller must be designed based on the stability conditions of the above system. Typical stability conditions are found in Refs.[5-7]. And the conditions are more conservative in the case of the system with uncertainties and time delays [11-12]. This makes it difficult to use linear control theories for the T-S fuzzy system. The best way of using linear control theories freely in the control of the T-S fuzzy system is the linearization. Therefore, the problem of this work is formulated as a linearization of T-S fuzzy system.

3 T-S fuzzy feedback linearization

A new linearization technique was proposed for the T-S fuzzy model under the following assumption.

Assumption 1: All of the linear models are controllable. i.e., the following condition is satisfied:

              (7)

This is a very common condition for most control systems. Under the above assumption, the following i-th rules of the fuzzy model were proposed to deal with the coordinate change for linearization.

Plant Rule i:

If λ₁(t) is F_i1, …, and λ_g(t) is F_ig

Then ,

                       (8)

and

                        (9)

for i=1, 2, …, L, where

By using product fuzzy inference and center- average defuzzifier, the overall z(t) could be rewritten as

                       (10)

which was considered as the summation of the states x(t) through transformation T_i with the proportion of h_i. After coordinate change, the overall fuzzy system was inferred from Eq.(9) as follows:

             (11)

The above system could be a linearizable form by determining T_i as follows.

Under assumption 1, the following T_i was obtained:

               (12)

where the parameters in A_ci are obtained from the following characteristic equation of the i-th local linear model:

          (13)

Then, the above state transformation T_i changed the i-th linear system into the following controllable canonical form:

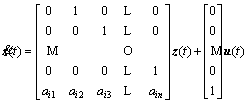     (14)

The overall fuzzy system with local linear models (Eq.(14)) is now a linearizable T-S fuzzy system:

(15)

where  and  from Eq.(4).

The following theorem presents a controller which linearizes the T-S fuzzy system.

Theorem 1: The following nonlinear feedback input linearizes the T-S fuzzy system into the controllable canonical form:

                 (16)

where the overall state z(t) is inferred in Eq.(1).

The proof is obvious from Eq.(15).

Fig.1 shows the overall description for the proposed linearization method.

Fig.1 Overall scheme of T-S fuzzy feedback linearization

4 Robust H_∞ control with SMC and lineari- zation

In this work, A T-S fuzzy system with uncertainties was considered and the robustness of SMC was added to the linearized T-S fuzzy system:

        (17)

where w_T(t)=w₁(t)+w₂(t), is lumped uncertainties including parameter uncertainties and disturbances and bounded by ||w_T(t)||<>_max, w₁(t) is the unmatched uncertainty and w₂(t) is the uncertainties satisfying the following matching condition:

 for i=1, …, L                 (18)

In order to design robust H_∞ controller with SMC, H_∞ controller was designed first and then SMC input was determined based on the sliding surface which has the dynamics of H_∞ controlled system.

In the linearized system, the uncertainties in the system (Eq.(17)) can also be classified into unmatched uncertainties w_u(t) and matched one w_m(t).

H_∞ controller was designed for the linearized system with the unmatched uncertainties only as follows:

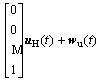                (19)

where u_H(t) is the H_∞ controller.

The effect of w_u(t) deteriorated the control performance of fuzzy control system. H_∞ control is one of the most effective designs to eliminate the effect of w_u(t) on the control system satisfying the following control performance [7]:

                        (20)

where t_f denotes the terminal time of the control, ρ is a prescribed value which denotes the worst case effect of w(t) on x(t), and Q is a positive-definite weighting matrix.

The physical meaning of Eq.(19) is that the effect of w(t) on x(t) must be attenuated below a desired level ρ from the viewpoint of energy, no matter what w(t) is, i.e., the L₂ gained from w(t) to x(t) must be equal to or less than a prescribed value ρ². In general, ρ is chosen as a positive small value less than 1 for the attenuation of w(t).

The H_∞ controller of this work is a state feedback u_H(t)=-Kz(t) where K is determined as K=YW^-1, and Y and W are the solutions of the following LMI’s [7]:

       (21)

If the LMI in Eq.(21) has a positive-definite solution for W, then the closed-loop system is stable and the control H_∞ performance in Eq.(20) is guaranteed for a prescribed ρ.

First, the virtual state was defined based on the following controllable canonical form of the nominal system:

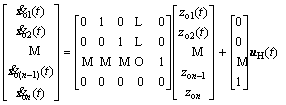(22)

The virtual state was defined as

         (23)

The sliding surface was defined as

     (24)

where

If the state of the system (Eq.(17)) is on the sliding surface (Eq.(25)), the state has the dynamic of the Eq.(20). To guarantee the state on the sliding surface, the following hitting condition must be satisfied:

                               (25)

The above condition is satisfied by the discontinuous control input presented in Theorem 2 [18].

Theorem 2: The SMC system with the following control input has the dynamics of the nominal optimal control system:

       (26)

(Proof) See the proof of Th1. in Ref.[18].

As mentioned in Theorem 2 and sliding mode control theory, the state x(t) follows the trajectory of the nominal system controlled by sliding mode control input v(t) which is designed to put the states of the system onto the sliding surface.

The following initial virtual state makes the initial value of S(z, z_v) equal to zero without reaching phase:

        (27)

5 Example and simulation results

To show the robustness of the proposed robust H_∞ controller and its performance, an example of a DC motor controlling an inverted pendulum via a gear train was considered [20].

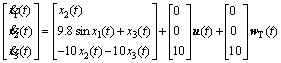 (28)

where x₁ is the angle of the pendulum, x₂ is the acceleration of the pendulum, x₃ is the current of driver DC motor, u is control voltage of DC motor, and w_T is disturbance.

The above system is described as

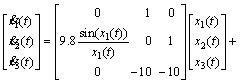
                  (29)

The local linear models in the T-S fuzzy model are as follows:

,,

                             (30)

The membership functions h₁(t) and h₂(t) are defined as

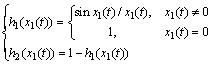          (31)

The membership functions are shown in Fig.2.

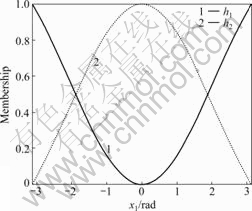
Fig.2 Membership function

This fuzzy model exactly represents the dynamics of the nonlinear mechanical system under -π≤x₁(t)≤π.

The state transformation matrices are obtained as

,      (32)

The controllable canonical forms are

, ,

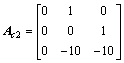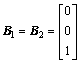                              (33)

From the above, the following vectors are identified:

,          (34)

Unmatched disturbance is assumed as

                  (35)

where s(t) is the square wave with the period of 6 s and amplitude of 0.5. The matched uncertainty is given as the same one with unmatched uncertainty.

With ρ²=0.216 2, the solution of LMI and controller gains are obtained as

The following H_∞ controller for the linearized system is used.

                 (36)

The virtual state is defined as follows:

             (37)

Sliding surface is given by

      (38)

By differentiating Eq.(38), the following equation is obtained:

                     (39)

The following novel sliding mode control input is obtained from the hitting condition:

 (40)

To eliminate reaching phase, the following initial virtual state must be set:

 (41)

To show the robustness of the proposed controller, it was compared with the H_∞ controller through the state responses with uncertainties. The simulation results are shown in Figs.3-7.

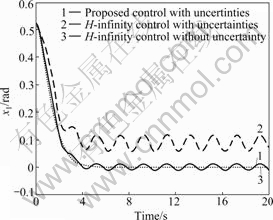
Fig.3 State trajectories of x₁

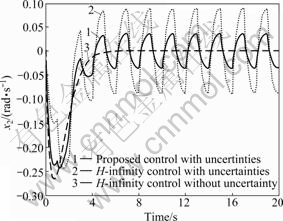
Fig.4 State trajectories of x₂

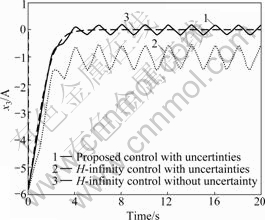
Fig.5 State trajectories of x₃

Under the same uncertainties, the state trajectories of the proposed controller are closer to the nominal trajectories than those of H_∞ control trajectories. This means that the proposed controller is more robust than

Fig.6 Control input of proposed controller

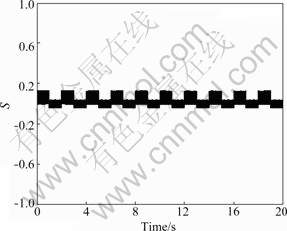
Fig.7 Sliding function

H_∞ controller. The proposed controller has the robustness of SMC which is robust for the matched uncertainties.

In Fig.6, the control input chattering is shown because of SMC characteristic and this is not critical because the elimination method for this kind of chattering is well-known already.

Fig.7 shows small value of sliding function and this means that the robustness is achieved sufficiently.

6 Conclusions

Novel linearization of T-S fuzzy model was proposed by using the T-S fuzzy state transformation and fuzzy feedback control. After linearization, LMI based H-infinity controller with SMC was used for the performance of H-infinity control and the robustness of SMC. This new linearization method can be classified as a kind of approximate linearization through T-S fuzzy system and makes many linear control theories useful for T-S fuzzy systems. This work must be extended to the case of multi-input.

References

[1] HO W H, TSAI J T, CHOU J H. Robust-stable and quadratic-optimal control for TS-fuzzy-model-based control systems with elemental parametric uncertainties [J]. IET Control Theory & Applications, 2007, 1(3): 731-742.

[2] HO W H, TSAI J T, CHOU J H. Robust quadratic-optimal control of TS-fuzzy-model-based dynamic systems with both elemental parametric uncertainties and norm-bounded approximation error [J]. IEEE Trans Fuzzy Systems, 2009, 17(3): 518-531.

[3] HSU M R, HO W H, CHOU J H. Stable and quadratic optimal control for TS fuzzy-model-based time-delay control systems [J]. IEEE Trans Man and Cybernetics Systems, Part A: Systems and Humans, 2008, 38(4): 933-944.

[4] KRUSZEWSKI A, WANG R, GUERRA T M. Nonquadratic stabilization conditions for a class of uncertain nonlinear discrete time TS fuzzy models: A new approach [J]. IEEE Trans Automatic Control, 2008, 53(2): 606-611.

[5] TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control [J]. IEEE Trans Man and Cybernetics Systems, Part A: Systems and Humans, 1985, 15: 116-132.

[6] TNANKA K, IKEDA T, WANG H O. Fuzzy regulators and fuzzy observers: Relaxed stability conditions and LMI-based designs [J]. IEEE Trans Fuzzy Systems, 1998, 6: 250-265.

[7] CHEN Bor-sen TSENG Chung-shi, UANG Huet-jian. Robustness design of nonlinear dynamic systems via fuzzy linear control [J]. IEEE Trans Fuzzy Systems, 1999, 7(5): 571-585.

[8] TNANKA K, WANG H O. Fuzzy control systems design and analysis: A linear matrix inequality approach [M]. New York: John Wiley & Sons Inc, 2001: 49-81.

[9] FENG Gang. A survey on analysis and design of model-based fuzzy control systems [J]. IEEE Trans Fuzzy Systems, 2006, 14(5): 676-697.

[10] MOHANMMAND N, LAM H K. Relaxed LMI-based stability conditions for Takagi–Sugeno fuzzy control systems using Regional-Membership-Function-Shape-Dependent analysis approach [J]. IEEE Trans Fuzzy Systems, 2009, 17(5):1221-1228.

[11] ZHAO Yan, GAO Hui-jun, LAM J, DU Bao-zhu. Stability and stabilization of delayed T-S fuzzy systems: A delay partitioning approach [J]. IEEE Trans Fuzzy Systems, 2009, 17(4):750-762.

[12] SOUZA F O, MOZELLI L A, PALHARES R M. On stability and stabilization of T–S fuzzy time-delayed systems [J]. IEEE Trans Fuzzy Systems, 2009, 17(6): 1450-1455.

[13] LEE H G, KIM Y M, JEON H T. On the linearization via a restricted class of dynamic feedback [J]. IEEE Trans AC, 2000, 45: 1385-1391.

[14] KHALIL H K. Nonlinear systems [M]. New Jersey: Prentice Hall, 2002: 505-544.

[15] LEE H G, ARAPOSTATHIS A, MARCUS S I. Linearization of discrete-time systems via restricted dynamic feedback [J]. IEEE Trans AC, 2003, 48: 1646-1650.

[16] YOUNG K D, UTKIN V I, OZGUNER U. A control engineer’s guide to sliding mode control [J]. IEEE Trans on Control Systems Technology, 1999, 7(3): 328-342.

[17] PARK S K, AHN H K. Nonconservative sliding mode control with the feedback linearization or nonlinear system [C]// Proceedings of the 39th IEEE Conference on Decision and Control. Sydney: 2000: 2210- 2216. (in Sydney)

[18] PARK S K, AHN H G. Robust optimal controller design with novel sliding surface [J]. IEEE Proc Control Theory Appl, 1999, 146(3): 242-246.

[19] LIUTANAKUL P, PIERFEDERICI S, TABAR F M. Application of SMC with I/O feedback linearization to the control of the cascade Controlled-Rectifier/Inverter-Motor drive system with small dc-link capacitor [J]. IEEE Trans Power Electro, 2008, 23: 2489-2499.

[20] KUSCHEWSKI J G, HUI S, ZAK S H. Application of feed forward neural networks to dynamical system identification and control [J]. IEEE Trans Control Systems Technology, 1993, 1(1): 37-49.

(Edited by YANG Bing)

Foundation item: Research financially supported by Changwon National University in 2009

Received date: 2010-03-28; Accepted date: 2010-06-24

Corresponding author: YOON Tae-Sung, Professor, PhD; Tel: +82-55-213-3634; E-mail: skpark@changwon.ac.kr