Trans. Nonferrous Met. Soc. China 24(2014) 1859-1865
Integrated identification method of rheological model of sandstone in Sanmenxia bauxite
Chun-yang ZHANG1, 2, Ping CAO2, Cheng-zhi PU2, Jie LIU2, Pi-hua WEN3
1. School of Resources and Environment Engineering, Wuhan University of Technology, Wuhan 430070, China;
2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
3. School of Engineering and Materials Science, Queen Mary University of London, Mile End Road, London E1 4NS, UK
Received 23 March 2013; accepted 25 March 2014
Abstract:
Based on the uniaxial compression creep experiments conducted on bauxite sandstone obtained from Sanmenxia, typical creep experiment curves were obtained. From the characteristics of strain component of creep curves, the creep strain is composed of instantaneous elastic strain, εme, instantaneous plastic strain, εmp, viscoelastic strain, εce, and viscoplastic strain, εcp. Based on the characteristics of instantaneous plastic strain, a new element of instantaneous plastic rheology was introduced, instantaneous plastic modulus was defined, and the modified Burgers model was established. Then identification of direct screening method in this model was completed. According to the mechanical properties of rheological elements, one- and three-dimensional creep equations in different stress levels were obtained. One-dimensional model parameters were identified by the method of least squares, and in the process of computation, Gauss-Newton iteration method was applied. Finally, by fitting the experimental curves, the correctness of direct method model was verified, then the examination of posterior exclusive method of the model was accomplished. The results showed that in the improved Burgers models, the rheological characteristics of sandstone are embodied properly, microscopic analysis of creep curves is also achieved, and the correctness of comprehensive identification method of rheological model is verified.
Key words:
uniaxial compression creep experiments; instantaneous plastic rheological model element; improved Burgers model; direct screening method; posterior exclusive method;
1 Introduction
So far, most bauxite resources have been mined out by open-pit mining, but with the depletion of the bauxite resources in shallow earth in recent years, it becomes a trend that underground mining researches will be conducted for the development of bauxite resources [1,2]. Due to the natural existence condition and the properties of surrounding rocks, the major problem faced in underground mining is how to ensure the roadway stability. An important influence on the long-term stability of roadway will be exerted by the rheological properties of surrounding rocks, so extensive researches have been conducted previously. Based on the Burgers model, BAI et al [3] performed study on the roadway stability to provide guidance to the design of roadway support in Malin Coalmine. WANG et al [4] conducted researches on the effects of the rheological factors on the economical and effective support methods. LU et al [5] proposed that the highly resistant and yielding support system was beneficial to the long term stability of the broken soft rock in depth. The study carried out by ZHAO et al [6] on the roadway support in soft rocks showed that rheological behavior was the main factor involved in roadway deformation in depth. LI et al [7] believed that mastering the fractures development is very important to maintain the stability of soft rock roadway.
Many scholars have conducted relevant researches about rheological model. For example, a nonlinear rheological model [8] was introduced to study long-term stability of backfill material in roadway, and the engineering practice comparative analysis indicated its correctness. GRGIC et al [9] used two constitutive laws to analyze the phenomena involved in the mining collapses. YANG and CHENG [10] put forward a new non-stationary and nonlinear visco-elastic shear creep model, and the experimental data verified its reasonability. HOXHA et al [11] established a creep model describing primary and inverse creep of gypsum rock. In their research, the new model fitted better laboratory results and allowed describing of the accelerated creep.
In the identification process of rheological model, based on the practical rheological curves, the analysis and generalization are required to choose or establish the rheological model. The combination of direct screening method and posterior exclusive method was applied [12].
With respect to instantaneous plastic strain, OIKAWA1 and SUGAWARA [13] indicated that transient plastic strain generated as temperature increased. YUAN et al [14] mentioned instantaneous plastic strain in their article too. However, the definition of the instantaneous plastic strain and the derivation of the constitutive equation were not made in these work. LI et al [15] proposed instantaneous plastic strain constitutive equation, but the applicability was limited due to the requirement of great number of parameters.
There are many identification methods for model parameters, and some scholars have also identified rheological model parameters which contribute to the feasibility of model examination [16-18].
2 Experimental data analysis and rheological model establishment
Loading and unloading creep experiments of sandstone in natural condition were carried out on the computer controlled rock shear rheometer (RYL-600). In the experiment process, the mode of graded incremental cycle was applied and the unloading processes were force controlled. Samples were strictly processed in accordance with the requirements of international rock mechanics test, and the dimensions were d 50 mm × 100 mm. Three typical loading and unloading curves of sandstone samples are shown in Fig. 1.
Data analysis indicates that creep curves exhibit both the instantaneous elastic deformation and the instantaneous plastic deformation. If ε represents the total strain of a sample, εme represents instantaneous elastic strain, εmp represents instantaneous plastic strain, εce represents viscoelastic strain, εcp represents viscoplastic strain, then ε=εme+εmp+εce+εcp. The division of strain components is shown in Fig. 2.
Based on the characteristics of experimental curves, preliminary identification of rheological model is conducted. In this model, the elastic strain, εme, can be represented by the elastic element (H), the viscoelastic strain, εce, is represented by (H|N) element, and then the strain, εcp, can be represented by viscous element (N).
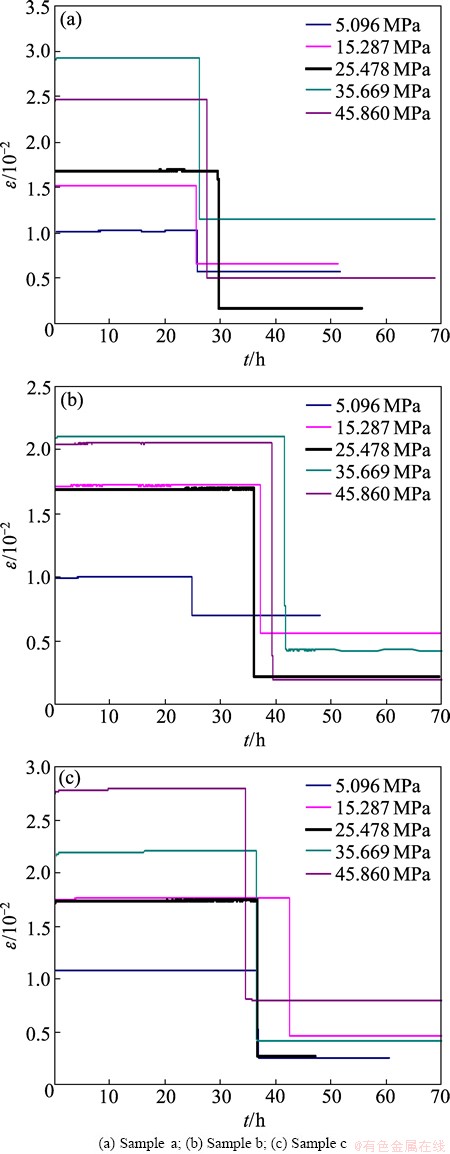
Fig. 1 Typical creep loading and unloading curves
Fig. 2 Strain components diagram
Because of the lack of the specific rheological element which represents the instantaneous plastic strain εmp, in this work, a new instantaneous plastic model element, in which P0 is defined as the instantaneous plastic modulus, and σs1 is defined as initial stress of instantaneous plastic deformation, is proposed, and the new model is shown in Fig. 3. Therefore, instantaneous plastic deformation εmp can be represented by new instantaneous plastic model element, and a modified Burgers model is established initially.
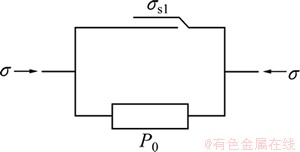
Fig. 3 Instantaneous plastic model element
In instantaneous plastic model, definition of P0 is the key of model establishment. Referring to the instantaneous elastic deformation, the ratio, σ/εme, in which σ is the loading stress and εme is the instantaneous elastic strain, is defined as the instantaneous elastic modulus E. Just as the instantaneous elastic deformation, instantaneous plastic deformation is caused in a very short time, therefore, the relationship among σ, εmp and t, can be simplified as the relationship between σ and εmp. Combined with the component of instantaneous plastic strain after separating, the accumulated instantaneous plastic strain under different stress levels is obtained. Because of the unrecoverable characteristic of instantaneous plastic deformation during unloading, the iterative equation of accumulated instantaneous plastic strain when stress ranges from 5.096 MPa to 45.860 MPa is shown in Eq. (1), and the accumulated values of instantaneous plastic strain under different stress levels are shown in Table 1.
(1)
where εmp1, εmp2, εmp3, …, εmpn are the accumulated values of instantaneous plastic deformation under different stress levels, respectively.
Table 1 Accumulated values of instantaneous plastic strain
Linear fittings of the accumulated instantaneous plastic strain are shown in Fig. 4, in which the correlation coefficients, R2, of the samples approximately ranges from 0.95 to 0.97. It can be concluded that the relationship between σ and εmp is linear when the sample is loaded, so the instantaneous plastic modulus P0 can be defined as
(2)
where σ0 (σ0=σ-σs1) is the stress of instantaneous plastic element. Under the action of stress σ, the strain of the model is defined as
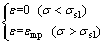(3)
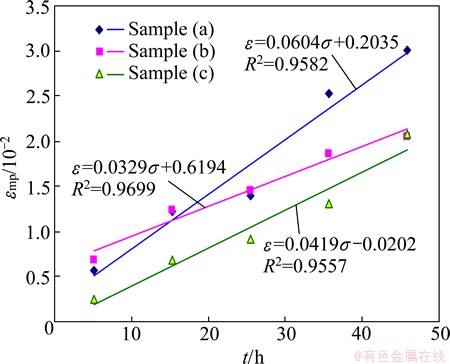
Fig. 4 Relationship between εmp and σ
It can be concluded from above analysis that the creep constitutive model shown in Fig. 5 is composed of instantaneous elastic element (H), instantaneous plastic element, viscoelastic element (H|N) and viscous deformation element (N) under uniaxial compression. This model is built on the basis of both loading and unloading conditions, so it is suitable for analysis of decay or steady-state creep in the loading and unloading processes.
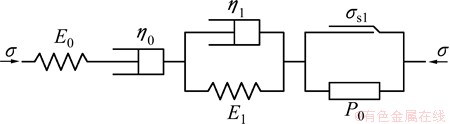
Fig. 5 Modified Burgers model
3 Formulae derivation of one-dimensional creep model
1) When σ<σs1, the model regresses to Burgers model. The derivation process of creep formulae is shown as
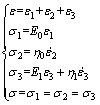(4)
The constitutive equation which is obtained by eliminating ε1, ε2 and ε3 is shown as
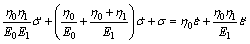(5)
The creep equation of Burgers model can be obtained by applying Laplace transform or superposition principle in Eq. (5) as
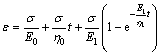(6)
2) When σ>σs1,
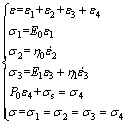(7)
The constitutive equation is shown as follows:
(8)
And the creep equation can be written as
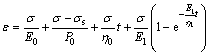(9)
According to one-dimensional creep equation, model characteristic curves can be obtained. When σ<σs1, the characteristic curves are the same as Burgers model. When σ>σs1, the characteristic curves are shown in Fig. 6, in which σ is a constant equal to σ0.
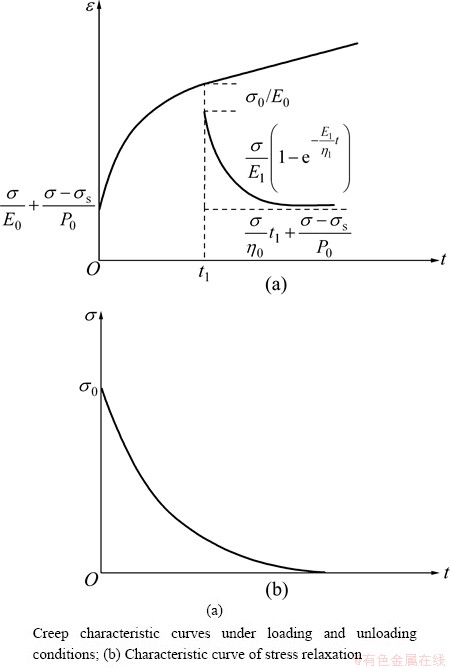
Fig. 6 Characteristic curves of modified Burgers model
4 Formulae derivation of three-dimensional creep model
Based on the tensor theory, under three-dimensional conditions, tensors can be decomposed into the spherical stress tensor σm and the deviatoric stress tensor Sij. In general, the change in material volume is caused by the spherical tensor σm, and the change in shape is caused by deviatoric tensor Sij. Stress σij presented in the form of tensor is shown as
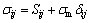(10)
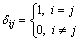(11)
where δij is a spherical unit tensor.
As shown in Eq. (12), strain tensor can also be decomposed into the spherical strain tensor εm and the deviatoric strain tensor εij:
(12)
Under different axial stress, three-dimensional creep formulae of new model are shown as follows.
1) When σ<σs1,
(13)
2) When σ>σs1,
(14)
where G0 and G1 are the shear modulus. The conversions among elastic constants are shown in Eq. (15). Combining with the rule on instantaneous plastic modulus P0, 
which can be written as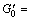 
is obtained on the assumption that has a similar definition as G0.
(15)
Based on the creep formulae of new model under three-dimensional condition, the creep equations under triaxial stress can be derived. In creep experiments, σm 
can be obtained on the assumption that no confining stress is applied (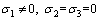
). Therefore, the creep stress can be expressed in the form of tensors as
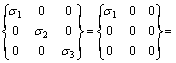
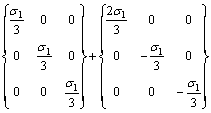(16)
The triaxial creep equations of the modified Burgers model (the confining pressure is zero) are shown as follows.
1) When σ<σs1,
(17)
2) When σ>σs1,
(18)
where K is the volume deformation modulus; ε1 is the axial creep equation without confining stress; ε2 and ε3 are the lateral creep equations without confining stress. The lateral creep data can also be fitted by the lateral creep equation.
5 Model parameter identification
In the one-dimensional model, least squares method is applied to the indentation process of parameters and Gauss-Newton method is adopted in the calculation process. Parameters, such as E1, η0, η1, can be obtained by substituting the separated instantaneous elastic and plastic strain into creep formula. Because of the linear relationship between instantaneous elastic, plastic strain and load stress, E0 and P0 can be obtained as
(19)
After the identification of parameters in the modified Burgers model, the creep experimental data of sandstone are fitted using the calculated data. The identification results of parts rock sample (b) are shown in Table 2, and the fitting results are shown in Fig. 7.
As shown in Fig. 7, the fitting correlation coefficient, R2, of the modified Burgers model is high. The results again prove the correctness of the new model. According to the parameter indentation and the analysis of fitting results, the model examination by using posterior exclusive method is completed. Based on the program interface provided by FLAC3D, secondary development of the new model can be carried out to analyze the long-term stability of roadway after excavation.
Table 2 Modified Burgers model identification parameters of rock sample (b)
Fig. 7 Sandstone rheological model fitting curves
6 Conclusions
1) Based on the analysis of sandstone creep data and the mechanical characteristics of each strain component, instantaneous plastic element and instantaneous plastic modulus P0 were defined. Physical equation of the instantaneous plastic modulus P0 was derived by conducting analysis on the relationship among σ, εmp and t. According to the direct selection method, the modified Burgers model was established initially by series-parallel combination of different model elements.
2) Based on the mechanical characteristics of model elements, one-dimensional creep equation of the modified Burgers model was derived. Combined with the three-dimensional tensor theory, three-dimensional creep equations of the model under different stress conditions were continuously derived.
3) Based on the creep experimental data, Gauss-Newton iterative calculation for the modified Burgers model was carried out, and basic parameters of the model were identified. The results show that the model can be used to fit the experimental curves properly, and the correlation coefficient R2 is high, the correctness of new model established by using direct selection method was proved once again, and the model identification by applying posterior exclusive method was also completed.
References
[1] NAGHADEHI M Z, MIKAEIL R, ATAEI M. The application of fuzzy analytic hierarchy process (FAHP) approach to selection of optimum underground mining method for Jajarm Bauxite Mine, Iran [J]. Expert Systems with Applications, 2009, 36 (4): 8218-8226.
[2] ZHOU Ke-ping, CHEN Qing-fa, HU Jian-hua. Concept of the mining environment reconstructing continuous mining in underground bauxite [J]. Journal of Guangxi University, 2008, 33(2): 168-172. (in Chinese)
[3] BAI Qi-shu, XIA Yuan-you, LIU Xin-xi, YANG Zi-han. Mining roadway support technology based on rheological analysis in malin coalmine [J]. Energy Procedia, 2012, 16: 1129-1134.
[4] WANG C, WANG Y, LUB S. Deformational behaviour of roadways in soft rocks in underground coal mines and principles for stability control [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(6): 937-946.
[5] LU Yin-long, WANG Lian-guo, ZHANG Bei. An experimental study of a yielding support for roadways constructed in deep broken soft rock under high stress [J]. Mining Science and Technology, 2011, 21(6): 839-844.
[6] ZHAO Guo-zhen, MA Zhan-guo, ZHU Qing-hua, MAO Xian-biao, FENG Mei-mei. Roadway deformation during riding mining in soft rock [J]. International Journal of Mining Science and Technology, 2012, 22(4): 539-544.
[7] LI Xue-hua, YAO Qiang-ling, MAN Jian-kang, CHEN Chao-qun, HE Li-hui. Development of fractures in soft rock surrounding a roadway and their control [J]. Mining Science and Technology, 2011, 21(4): 573-579.
[8] ZHANG Tian-jun, MA Mi-na, WANG Hong-sheng, XU Hong-jie. A nonlinear rheological model of backfill material for retaining roadways and the analysis of its stability [J]. Mining Science and Technology, 2011, 21(4): 543-546.
[9] GRGIC D, HOMAND F, HOXHA D. A short- and long-term rheological model to understand the collapses of iron mines in Lorraine, France [J]. Computers and Geotechnics, 2003, 30(7): 557-570.
[10] YANG Sheng-qi, CHENG Long. Non-stationary and nonlinear visco-elastic shear creep model for shale [J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(6): 1011-1020.
[11] HOXHA D, GIRAUD A, HOMAND F. Modelling long-term behaviour of a natural gypsum rock [J]. Mechanics of Materials, 2005, 37(12): 1223-1241.
[12] WANG Zhi-ying, LI Yun-peng. Rock rheology theory and its numerical simulation [M]. Beijing: Science Press, 2008. (in Chinese)
[13] OIKAWA1 H, SUGAWARA K. Instantaneous plastic strain associated with stress increments during the steady state creep of Al and Al-5.5 At. Pct. Mg alloy [J]. Scripta Metallurgica, 1978, 12(1): 85-89.
[14] YUAN Hai-ping, CAO Ping, WAN Wen, XU Wang-zhong. Study on creep rules of soft and intricate ore-rock under step load and unload [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(8): 1575-1581. (in Chinese)
[15] LI Liang-quan, XU Wei-ya, WANG Wei. A nonlinear viscoelastoplastic rheological model based on Nishihara’s Model [J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(5): 671-680. (in Chinese)
[16] GAVRUS A, MASSONI E, CHENOT J L. An inverse analysis using a finite element model for identification of rheological parameters [J]. Journal of Materials Processing Technology, 1996, 60(15): 447-454.
[17] LEWANDOWSKI R, CHORAZYCZEWSKI B. Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers [J]. Computers & Structures, 2010, 88(2): 1-17.
[18] XIA Cai-chu, XU Chong-bang, WANG Xiao-dong, ZHANG Chun-sheng. Method for parameters determination with unified rheological mechanical model [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(2): 425-432. (in Chinese).
三门峡铝土矿砂岩流变模型的综合辨识方法
张春阳1, 2，曹 平2，蒲成志2，刘 杰2，文丕华3
1. 武汉理工大学 资源与环境工程学院，武汉 430070；
2. 中南大学 资源与安全工程学院，长沙 410083;
3. School of Engineering and Materials Science, Queen Mary University of London, Mile End Road, London E1 4NS, UK
摘 要：通过对三门峡铝土矿砂岩进行单轴压缩蠕变实验，获取该类岩石的蠕变实验曲线。通过分析蠕变曲线各应变分量特征，将蠕变总应变细分为瞬时弹性应变εme、瞬时塑性应变εmp、黏弹性应变εce、黏塑性应变εcp。根据瞬时塑性应变数据特征，引入新的瞬时塑性原件，定义瞬时塑性模量，建立改进的伯格斯(Burgers)流变模型，完成模型的直接筛选法辨识。根据模型元件力学性质，推导模型在不同应力等级下的一维和三维蠕变方程。采用最小二乘法辨识一维模型各参数，迭代时采用高斯-牛顿法计算，最后拟合实验曲线，验证直接法模型建立的正确性，完成模型后验排除法检验。研究表明，改进的伯格斯模型较好地描述了砂岩流变特征，实现砂岩流变曲线的微观分析，此外，也验证了流变模型综合辨识方法的正确性。
关键词：单轴压缩蠕变实验；瞬时塑性流变模型元件；改进的伯格斯模型；直接法；后验排除法
(Edited by Sai-qian YUAN)
Foundation item: Projects (51174228, 51274249) supported by the National Natural Science Foundation of China
Corresponding author: Ping CAO; Tel: +86-13973128263; E-mail: pcao_csu@sina.com
DOI: 10.1016/S1003-6326(14)63264-7
Abstract: Based on the uniaxial compression creep experiments conducted on bauxite sandstone obtained from Sanmenxia, typical creep experiment curves were obtained. From the characteristics of strain component of creep curves, the creep strain is composed of instantaneous elastic strain, εme, instantaneous plastic strain, εmp, viscoelastic strain, εce, and viscoplastic strain, εcp. Based on the characteristics of instantaneous plastic strain, a new element of instantaneous plastic rheology was introduced, instantaneous plastic modulus was defined, and the modified Burgers model was established. Then identification of direct screening method in this model was completed. According to the mechanical properties of rheological elements, one- and three-dimensional creep equations in different stress levels were obtained. One-dimensional model parameters were identified by the method of least squares, and in the process of computation, Gauss-Newton iteration method was applied. Finally, by fitting the experimental curves, the correctness of direct method model was verified, then the examination of posterior exclusive method of the model was accomplished. The results showed that in the improved Burgers models, the rheological characteristics of sandstone are embodied properly, microscopic analysis of creep curves is also achieved, and the correctness of comprehensive identification method of rheological model is verified.
