自适应的over-relaxed快速动态均值漂移算法
杨 斌1，赵 颖2，樊晓平2，周芳芳2
(1. 清华大学 计算机科学与技术系 智能技术与系统国家重点实验室，北京，100084；
2. 中南大学 信息科学与工程学院，湖南 长沙，410075)
摘 要：
摘 要：为了解决高斯核均值漂移算法收敛速度慢、计算效率不高的问题，提出自适应over-relaxed快速动态更新方法改进高斯核均值漂移算法。首先，在静态均值漂移算法中引入数据集的动态更新机制，每次迭代后将数据集更新到新的数据点，然后，将迭代过程中聚集在一起的数据点用1个收敛点表示，逐步减少参与计算的数据，保证准确性的同时降低计算量。由于非正态分布的数据集动态更新时，主方向上的数据点的收敛速度较慢，采用over-relaxed的策略来提高主方向数据点的迭代步长，并根据数据集直径的变化，自适应地计算步长参数。实验结果表明，改进后的高斯核均值漂移算法以超线性的速度收敛，收敛点的应用降低了收敛过程中的计算量。
关键词：
中图分类号：TP301 文献标识码：A 文章编号：1672-7207(2008)06-1296-07
Adaptive over-relaxed fast dynamic mean shift
YANG Bin1, ZHAO Ying2, FAN Xiao-ping2, ZHOU Fang-fang2
(1. State Key Laboratory of Intelligent Technology and Systems, Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China;
2. School of Information Science and Engineering, Central South University, Changsha 410075, China)
Abstract: An adaptive over-relaxed fast dynamic mean shift was proposed to speed up the convergence of Gaussian mean shift. Firstly, the convergence speed of Gaussian mean shift was improved by dynamically updating the data set and the number of the data set decreased using a special point replacing the points overlapped during the iterations. Secondly, as the data set didn’t follow the normal distribution, the direction of principal component converged more slowly than other directions. So the convergence of the data in the direction of principle component was accelerated by the over-relaxed strategy and the parameter was adaptively calculated by the diameter of the dynamic data set. The experimental results prove that the convergence speed of the proposed method is non-linear and the use of convergence points can lower the complicacy of process of iteration.
Key words: mean shift; Gaussian kernel; bound optimization; dynamic update
均值漂移算法是一种高效的统计迭代算法，它由核密度估计公式推导获得[1]，能在特征空间中沿数据集密度上升的方向搜索到局部极值[2]。由于不需要先验知识并且计算简单，适合对未知的数据集进行分析，近年来，均值漂移算法被广泛应用于模式分类[3-4]、图像分割[5-6]和视频跟踪等领域[7-9]。均值漂移算法的收敛性由核函数决定[10]，常用的核函数有均匀核、Epanechnikov核和高斯核，但是，它们的收敛速度各不相同。均匀核和Epanechnikov核计算简单，收敛速度快，但计算精度不高。高斯核函数计算精度高，分类效果好[5]，收敛路径平滑，但收敛速度慢。因此，在处理大规模的高维数据时，很少采用高斯核均值漂移算法。在此，本文作者主要针对高斯核均值漂移算法的收敛速度和计算效率进行改进。为了提高高斯核均值漂移算法的收敛速度，扩大算法的应用范围，近年来，一些研究者对均值漂移算法的原理进行了深入研究，提出通过减少迭代次数和降低每次迭代的计算量的方法来提高算法的效率[11]。Cheng等[2, 12]提出了在均值漂移算法中引入数据集的模糊机制，每次迭代后更新数据集，直到数据点收敛到局部极值点为止。Fashing等[13]证明，当核函数是连续函数时，均值漂移算法是一种边界优化算法。Carreira[14]则进一步证明了高斯核均值漂移算法类似于EM(Expectation Maximization)算法。Salakhutdinov提出了over-relaxed策略来提高EM算法的收敛速度[15]。在数据量很大时，上述算法的速度和准确性均不高。本文作者提出自适应的over-relaxed快速动态均值漂移算法。该算法首先在标准的均值漂移算法中引入动态更新的机制，每次迭代后，将数据点“漂移”到均值点处，使数据点迅速地收敛到极值点，减少了迭代次数。同时，在每次迭代过程中，将聚集在一起的数据点用1个收敛点表示，该收敛点的权值为聚集点的权值之和，减少了数据量，降低了每次迭代的计算量。当数据集不满足正态分布时，数据集各维度的收敛速度各不相同，非主方向的收敛速度快，主方向上的数据点收敛速度慢。为此，采用over-relaxed的策略来提高主方向上数据点的步长，并根据数据集各维度的直径的变化来自适应的计算步长参数。
1 快速的动态高斯核均值漂移算法
1.1 标准高斯核均值漂移算法
给定d维空间Rd中的n个采样点S={xi, 1≤i≤n}，由于高斯轮廓函数k(x)= exp(-x/2) (x＞0) 满足非负、非增和连续的特点，因此对应的高斯核函数为： KN(x) = (2π)-d/2exp(-||x||2/2) (x＞0)。根据KN(x)及带宽h，密度函数f的高斯核密度估计公式为：
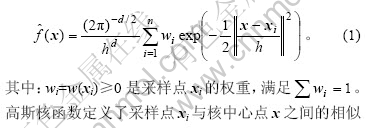
其中：wi=w(xi)≥0是采样点xi的权重，满足
。高斯核函数定义了采样点xi与核中心点x之间的相似性度量，xi与x之间的距离越近，相似度越高；距离越远，相似度越低。带宽h决定了核函数的影响范围，概率密度估计f(x)是每个采样点处的高斯核函数加权求和的结果。搜索密度极值点就是寻找密度梯度为零的采样点，即
，因此，
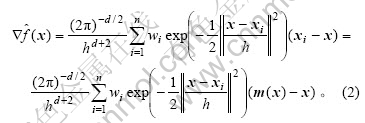
令M(x)=m(x)-x，称作均值漂移向量，表示迭代的步长，其中：
式(3)为均值漂移迭代公式，它表示采样点的加权平均值，类似于“重心”的概念，因此，m(x)处的密度一般大于x处的密度。由式(1)~(3)可得：
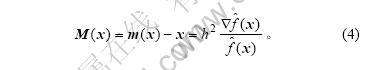
由式(4)可知均值漂移向量M(x)的方向总是指向密度大的方向，均值漂移算法的收敛点为密度极大值点。均值漂移算法的过程为：首先从S中随机地选择数据点xi作为起始点，然后，根据式(3)对该点不断地迭代更新，直到收敛到局部密度极大值点为止。对数据集中的其他点进行类似均值漂移，可以获得数据集中所有的极值点。最后，将距离接近的极值点合并为1个极值点。
1.2 快速的动态均值漂移算法
在标准高斯核均值漂移算法中，数据集S固定不变，路径点T不断更新。为了提高高斯核均值漂移算法的收敛速度和计算效率，首先，采用数据集的动态更新机制来减少迭代次数，并通过合并近距离的采样点来降低数据集的采样点个数，降低迭代的计算量。动态的均值漂移算法对数据集S和路径T同时进行更新，每次迭代都计算数据集中每个数据点的均值漂移向量，并对数据点进行更新，下一次迭代则在新的数据集上进行，最后，数据点收缩到局部极值点。
假设数据集S={xi, 1≤i≤n}服从正态分布N(μ, σ2)，其中，μ为均值，σ2为方差。由大数定律可得式(2) 中的高斯核密度估计函数f分布服从正态分布 N(μ, σ2+h2)。因此，由中心极限定理可得密度估计f(x)的均值也呈正态分布：
。由于梯度是线性运算，所以，梯度估计的均值为：
[15]。均值漂移算法的步长为：
其中：plim表示概率的极限。文献[12]证明了当数据集服从正态分布时，动态更新后的数据集合仍然满足正态分布，均值μ不变，方差σ2减小为
，
，即各个方向的收缩速度相同。而当数据集不满足高斯分布时，数据点亦会收缩，极值点保持不变，但是，各个方向数据点的收缩速度不同，主方向上的数据点收缩速度慢，非主方向上的数据点收缩速度快。
动态均值漂移算法虽然使数据点逐渐地收缩到极值点，但是，数据集的数目始终保持不变，数据点逐渐重叠在一起，而每次迭代都需要计算数据点与周围n-1个数据点的距离。为了减少每一次迭代的计算量，本文作者提出将重叠的数据点用1个收敛点表示，该点的权值是所有重叠点的权值之和。
定义1 当数据集G={xi, i = 1, …, l}中的点重叠在一起时，即
(i, j = 1, …, l且i≠j)，可以用1个点c=(wc, nc)来表示数据集G。其中：点c的权值为
；nc=l，为记录重叠的数据点的数目。因此，称c为G的收敛点。
用收敛点计算均值漂移算法不会影响算法的准确性，并显著地降低了每次迭代的计算量，尤其是接近密度极值点时，数据点数目显著下降，计算速度得到很大提高，迭代结束时的收敛点就是所求的极值点，将收敛到同一个极值的数据点划分为一类，实现了数据点的分类。
快速的动态均值漂移算法的停止规则是当数据集中只剩下极值点时，就可以结束迭代，因此，可以比较连续2次迭代后数据集中数据量的个数：当数据量不变，即n(t) = n(t+1)时，表示可以结束迭代。通过实验发现，当数据集中包含多种模式时，数据点可能会收敛到鞍点，降低了算法的准确性。通常情况下，收敛到鞍点的数据点的个数非常少，远小于收敛到峰值点处的数据点个数。因此，可以通过判断收敛点c中的nc将鞍点中的数据点归并到离峰值点最近的一类中。快速的动态均值漂移算法在不影响算法的准确性的情况下，通过减少数据集的数据量降低算法的计算量。
2 自适应的over-relaxed二次边界优化算法
2.1 二次边界优化算法的证明
由于当数据集不满足正态分布时，主方向的数据点收敛速度慢。下面证明动态的均值漂移算法是一种二次边界优化算法，并采用over-relaxed策略来提高主方向的收敛速度。
在模式识别和机器学习领域中，很多问题都可以通过优化某个目标函数来解决。当目标函数具有某些特殊结构时，可以利用该结构，得到目标函数的边界函数，并通过优化边界来求解目标函数[13]。在理想情况下，边界函数在参数空间中有效，容易被优化，在某些点处等于目标函数。
定义2 设q(x)为目标函数，x∈X。若存在函数p(x)，在切点处x0处满足q(x0) = p(x0)，在其他点满足p(x)≤q(x)，则函数p(x)称作q(x)的边界函数。
若边界函数p(x)切于目标函数q(x)，并且最大化边界函数p(x)的计算量远小于直接计算目标函数q(x)，则可以根据p(x)构造边界优化算法。边界优化算法通过搜索静态点来计算边界函数p(x)的最大值，求解目标函数q。可以证明标准的和动态的高斯核均值漂移算法是二次的边界优化算法。
定理1 高斯核密度估计f(x)的边界函数为：
。
其中：a为常数。高斯核均值漂移算法能最大化边界函数p(x)，因此，高斯核均值漂移算法是二次边界优化算法。
证明 首先证明p(x)是高斯核密度估计函数f(x)的边界函数。
记r=||(x-xi)/h||2，将p(x)和f(x)看作为r的函数，此时，
； (6)
。 (7)
k为高斯轮廓函数，p为r的线性函数，称为超平面。令p(x0) = f(x0)，求得：
。
此时，p(x)在x0处与f(x)相切，p(x)为与f(x)相切的超平面。由于高斯轮廓函数k(x)为凸函数，密度估计函数f(x)是高斯核函数的加权和，因此，f(x)亦为凸函数。因为超平面p(x)在切点x0处，p(x0) = f(x0)，在其他地方，p(x)＜f(x)，满足定义1，所以，p(x)为f(x)的边界函数。
下面证明高斯核均值漂移算法可以最大化边界函数p(x)。
。 (8)
式(8)和式(2)相同，当x＝x0时，在切点处
，取极大值。因此，利用高斯核均值漂移算法可以求得边界函数p(x)的最大值，即高斯核均值漂移算法是边界函数p(x)的最大化算法。又由于p(x)是x的二次函数，即，p(x)为f(x)二次边界函数，高斯核均值漂移算法是二次边界优化算法。动态的均值漂移算法更新后的数据集是原数据集的子空间，因此，具有相同的属性，动态的均值漂移算法也是二次边界优化算法。
2.2 自适应的over-relaxed边界优化改进
动态的高斯核均值漂移算法与标准的均值漂移算法相比，收敛速度提高。但是，对于非正态分布的数据，主方向的收敛速度较慢，因此，需要提高主方向数据点的收敛速度。根据定理1的证明，动态的高斯核是二次的边界优化算法，可以通过over-relaxed边界条件对动态的均值漂移算法的收敛速度进行改进。Over-relaxed动态均值漂移算法的迭代公式为：
。 (9)
参数β控制收敛的步长，当β=1时，over-relaxed边界优化就是标准的均值漂移算法，而β＞1则表示加大迭代步长，使迭代算法更快的收敛到极值。若β太大，则迭代算法可能发散，而若太小，则起不到加快收敛速度的效果，所以，求最优化的参数β是over-relaxed边界优化算法的关键。文献[15]证明了当β∈(0, 2)时，边界优化算法一定收敛。然而，求解最优化的β的计算量太大，降低了迭代算法的效率，尤其是对动态的均值漂移算法，数据点不断收缩，无法求解全局的最优的β。为了提高主方向上数据点的收敛速度，根据数据集合结构的变化，自适应地计算β参数。通过计算数据集的直径的变化来自适应地更新各个维度的步长。
定义3 给定d维的欧拉空间Rd中的采样点S = {xi, 1≤i≤n}，xi = {xi1,…, xid }，计算ρ ={ρj = max(xij) – min(xij), i = 1, …, n, j = 1, …, d }，ρ为d×d的对角矩阵，ρj为对角线上的元素，称ρ为数据集的直径。
t次迭代后的数据集S(t)的直径为ρ(t)，据快速动态均值漂移算法，t+1次迭代后数据集S′(t+1)的直径为ρ(t+1)。2次数据集直径之比为γ =ρ(t) /ρ(t+1)。为了保证各个方向的收敛速度，根据γ求得自适应β。若γj(j = 1, …, d)很大，则说明其为非主方向，βj为1。若γj(j = 1, …, d)很小，说明其为主方向，因此，要加大数据点在该方向上的迭代步长。为了保证收敛的一致性，并不需要对所有的数据点增加步长，而是要对主方向上处于边界区域的点增加步长。因此，over-relaxed动态的均值漂移算法的步骤为：
a. 根据公式(4)计算均值漂移的步长M(x)，并将数据集S更新到S′；
b. 计算S和S′各个维度的直径，并求得γi (i=1, …, d)和γ的平均值γ′，计算βi=γ′/γi：
若βi＜1，则说明数据集在第i维度上直径变化很大，为非主方向，具有较快的收敛速度，不需要进行加速，βi＝1；
若1＜βi＜2，则说明数据集在第i维度直径变化不大，为主方向，βi＝βi；
若βi＞2，为了保证迭代算法不发散，βi＝2；
c. 计算数据集S中数据点的梯度值
和平均梯度值
，若数据点的梯度大于平均梯度值，则认为这些数据点为边界处的数据点，获得处于边界处的数据点的序号；
d. 根据β增大边界处的数据点的步长，更新数据集S；
e. 比较连续2次数据集中数据的数目，若相等则停止迭代；否则循环执行步骤a。
3 收敛速度和复杂度分析
当数据集服从正态分布时，快速动态均值漂移算法使数据集的方差逐渐地收敛到0，即：
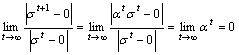。 (10)
因此，快速动态均值漂移算法满足超线性收敛。当数据集不服从高斯分布时，Over-relaxed加速后的数据集仍满足超线性收敛。而静态的高斯核均值漂移算法中，数据集的方差始终保持不变，
＜1，因此，采用标准的均值漂移算法时呈线性收敛[12]。
本文通过分析算法中数据点访问的次数来计算算法的复杂度。在静态的均值漂移算法中，数据点的计算次数约为t1dn2(其中：t1为平均迭代次数，d为数据点的维数，n为数据点的个数)。动态的均值漂移算法中，数据点的访问次数约为t2dn2(其中：t2为动态均值漂移算法的迭代次数)，因为采用动态的均值漂移算法时以超线性的速度收敛，而采用静态的均值漂移算法时以线性的速度收敛，因此，t1＞t2。快速的动态均值漂移算法的数据点的计算次数约为
(其中，n(t)为每次迭代数据点的个数，n＞n(t)＞n(t+1), t = 1, …, t2)。over-relaxed快速动态均值漂移算法的数据点计算次数为
，t2≥t3，与快速的动态均值漂移算法相比，每次迭代过程中数据点的数目 n(t)≥n′(t)。
4 实验结果
采用Matlab对算法进行运算，并对人工合成的数据进行实验。图1所示为快速动态均值漂移的过程。图2所示为over-relaxed的快速动态均值漂移算法的过程。从图2可以看出，非主方向的数据点的收敛速度提高。
(a) 第1次迭代；(b) 第2次迭代；(c) 第4次迭代；(d) 分类结果
图1 快速动态均值漂移算法
Fig.1 Fast dynamic MS
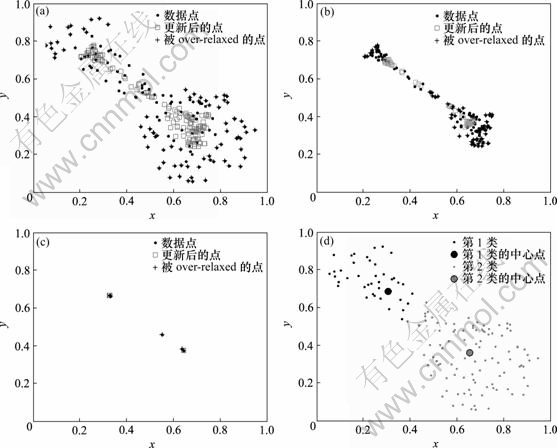
(a) 第1次迭代；(b) 第2次迭代；(c) 第4次迭代；(d) 分类结果
图2 Over-relaxed快速动态均值漂移算法
Fig.2 Over relaxed fast dynamic MS
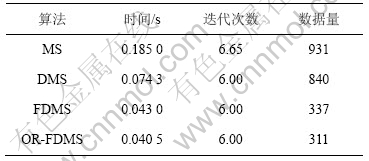
标准均值漂移算法(MS)、动态的均值漂移算法(DMS)、快速动态均值漂移算法(FDMS)和over-relaxed的快速动态均值漂移算法(OR-FDMS)的计算时间、迭代次数和数据点的访问次数如表1所示。可见，Over-relaxed快速动态均值漂移算法与标准的均值漂移算法、标准的动态漂移算法以及加速的动态均值漂移算法相比，计算速度分别提高78.1%，45.5%和5.81%。
表1 算法比较
Table 1 Comparisons of performance of algorithms
5 结 论
a. 在标准的均值漂移算法基础上引入数据集动态更新机制，每次迭代后将数据集更新到均值漂移点，实现了超线性的收敛速度。将聚集在一起的数据点合并为收敛点，逐渐减少数据点的数目，降低了每次迭代的计算量，提高了算法的效率。
b. 当数据集为非正态分布时，主方向收缩速度低于非主方向的收缩速度，采用over-relaxed策略来增加主方向上数据点的迭代步长，并利用数据集的直径自适应计算over-relaxed参数，进一步提高了主方向上的收敛速度。
参考文献：
[1] Fukunaga K, Hostetler L D. The estimation of the gradient of a density function, with applications in pattern recognition[J]. IEEE Transactions on Information Theory, 1975, 21(1): 32-40.
[2] Cheng Y Z. Mean shift, mode seeking, and clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 790-799.
[3] Comaniciu D. An algorithm for data-driven bandwidth selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(2): 281-288.
[4] Georgescu B, Shimshoni I, Meer P. Mean shift based clustering in high dimensions: A texture classification example[C]//IEEE International Conference on Computer Vision. New York: IEEE CS Press, 2003: 456-463.
[5] Comaniciu D, Meer P. Mean shift: A robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619.
[6] 王兆虎, 刘 芳, 焦李成. 一种基于视觉特性的遥感图像分割[J]. 计算机学报, 2005, 28(10): 1687-1691
WANG Zhao-hu, LIU Fang, JIAO Li-cheng. A remote sensing image segmentation algorithm based on vision information[J]. Chinese Journal of Computers, 2005, 28(10): 1687-1691.
[7] Comaniciu D, Ramesh V, Meer P. Kernel-based object tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5): 564-575.
[8] 彭宁嵩, 杨 杰, 刘 志, 等. Mean-Shift跟踪算法中核函数窗宽的自动选取[J]. 软件学报, 2005, 16(9): 1542-1550.
PENG Ning-song, YANG Jie, LIU Zhi, et al. Automatic selection of kernel-bandwidth for Mean-Shift object tracking[J]. Journal of Software, 2005, 16(9): 1542-1550.
[9] Collins R T. Mean-Shift blob tracking through scale space[C]// Processings 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Los Alamitos: IEEE Computer Society, 2003, 2: 234-240.
[10] 李乡儒, 吴福朝, 胡占义. 均值漂移算法的收敛性[J]. 软件学报, 2005, 16(3): 365-374.
LI Xiang-ru, WU Fu-chao, HU Zhan-yi. Convergence of a mean shift algorithm[J]. Journal of Software, 2005, 16(3): 365-374.
[11] Carreira-Perpinan M A. Acceleration strategies for Gaussian mean-shift image segmentation[C]//Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEEE CS, 2006: 543-549.
[12] Zhang K, Kwok J T, Tang M. Accelerated convergence using dynamic mean shift[C]//In the 9th European Conference on Computer Vision. New York: Springer, 2006: 257-268.
[13] Fashing M, Tomasi C. Mean shift is a bound optimization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(3): 471-474.
[14] Carreira-Perpinan M A. Gaussian mean shift is an EM algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(5): 767-776.
[15] Shen C, Brooks M J, Hengel A. Fast global kernel density mode seeking with application to localization and tracking[C]//IEEE International Conference on Computer Vision. Los Alamitos: IEEE Computer Society, 2005: 1516-1523.
收稿日期：2008-03-08；修回日期：2008-06-30
基金项目：国家自然科学基金资助项目(60433030)
通信作者：赵 颖(1980-)，男，湖南益阳人，讲师，从事虚拟现实、临场感、人工智能和情感计算等研究；电话：0731-2656373；E-mail: Zhaoying511@126.com
