DOI: 10.11817/j.issn.1672-7207.2018.10.030

动态失速下H型垂直轴风力机实时变桨控制规律

张立军¹，马东辰¹，赵昕辉¹，米玉霞¹，张松²，王旱祥¹，姜浩¹

(1. 中国石油大学(华东) 机电工程学院，山东 青岛，266580；

2. 中国石油大学(华东) 化学工程学院，山东 青岛，266580)

摘要：针对垂直轴风力机风能利用率低、自启动能力弱的问题，以1 kW H型垂直轴风力机为研究对象，通过对比美国Sandia国家实验室动态失速下测得的风力机实验结果与风洞静态实验结果，分析动态失速对桨距角调节的影响规律；以风轮的最大切向力为目标，得到垂直轴风力机在上风区和下风区的最佳理论攻角分别为14.8°和-14.8°。为使风轮在旋转过程中维持在最佳攻角附近，基于双致动盘多流管理论进行Matlab编程计算，建立风轮工作状态下的受力模型，获得垂直轴风力机在各个方位的桨距角。通过对0°和180°方位角下的桨距角进行修正，给出垂直轴风力机1周变桨距规律。最后，利用双致动盘多流管理论对提出的变桨控制规律进行理论验证。研究结果表明：利用该变桨距规律得到的风能利用率可以由34.6%提高到42.8%。

关键词：垂直轴风力机；动态失速；桨距角；最佳攻角；双致动盘多流管

中图分类号：KT83             文献标志码：A         文章编号：1672-7207(2018)10-2610-08

Real-time variable-pitch control laws of H-type vertical axis wind turbine under dynamic stall

ZHANG Lijun¹, MA Dongchen¹, ZHAO Xinhui¹, MI Yuxia¹, ZHANG Song², WANG Hanxiang¹, JIANG Hao¹

(1. College of Electromechanical Engineering, China University of Petroleum, Qingdao 266580, China;

2. College of Chemical Engineering, China University of Petroleum, Qingdao 266580, China)

Abstract: Aiming at the disadvantages of low efficiency and poor self-starting ability of vertical axis wind turbine, the study takes 1 kW H-type vertical axis wind turbine as the research object, the influence of dynamic stall on pitch angle adjustment was analyzed by contrasting the experimental results of wind turbine measured by dynamic stall at Sandia National Laboratory. The maximum tangential force of the wind wheel was regarded as the target, and the theoretical optimum angles of attack 14.8° and -14.8° at upwind area and downwind areas of wind turbine were obtained, respectively. In order to keep the wind wheel near the optimum angle of attack, the programming calculation in Matlab software based on double-multiple streamtubes theory was carried out, and the force model of the wind turbine was established and the pitch angle of the vertical axis wind turbine in each direction was obtained. By adjusting the pitch angle of 0° and 180° azimuth angle, the rule of the variable pitch of a vertical axis wind turbine was given. Finally, the proposed real-time variable-pitch control laws were verified based on the multi flow management theory of double actuated disk. The results show that the wind energy utilization rate can be increased from 34.6% to 42.8% by using the variable pitch.

Key words: vertical axis wind turbine; dynamic stall; pitch angle; optimum angle of attack; double-multiple stream tubes

由于能源危机日益严重，风能以其绿色、无污染、可再生等特点受到人们的广泛关注。我国风能资源丰富，根据国家气象局资料，我国近海70 m高度年平均风功率密度可达300 W/m²以上，大于6 m/s风速的累计时间可达4 000 h。风力发电机根据风轮旋转轴相对地面的安装角度分为垂直轴风力发电机(VAWT)和水平轴风力发电机(HAWT)，其中，垂直轴风力发电机以其无需安装对风装置、易于安装和维修等优点，越来越受到人们的关注。然而，现有商业H型垂直轴风力发电机风能利用率仅在30%~35%之间，且存在自启动能力弱等不足，在很大程度上限制了其规模化发展和应用。在垂直轴风力机旋转过程中，叶片攻角随方位角不断变化，不能维持在最佳攻角处，是其风能利用率低的主要原因^[1]。通过改变桨距角以达到调节攻角的目的是改善风力机风能利用率的主要途径。曹成帅等^[2]针对风剪、湍流等影响因素，提出基于系统分解的独立变桨距控制策略，通过将互不耦合子系统叠加得到变桨距变化规律；廉正光等^[3-4]利用双曲柄调距机构及双偏心轴机构，设计了一种新型调距机构，并且采用该机构制造出风力发电机样机；赵振宙等^[5]采用扰流技术，通过适当增大0°和180°处扰流角以提高风力机的整体性能；梁云峰等^[6]针对变速恒频风力发电机组的功率控制，设计了一套可以实现快速控制的液压变桨距系统。 上述研究提出的叶片桨距角调节方法在一定程度上可以提高风能利用率，改善风力机启动性能，但所运用的气动参数是在静态失速条件下设定的，未考虑动态失速的影响，而翼型的静态结果^[7]是在风轮固定不动时，通过风洞实验测得的各个攻角下的升阻力系数, 这不能真实反映风力机的实际工作状况。垂直轴风力机在正常工作中，叶片攻角随方位角不断变化总会发生动态失速^[8]。因此，有必要研究动态失速下垂直轴风力机桨距角调节方法，得出动态失速下叶片桨距角随方位角的变化规律，以提高风能利用效率。

1  动态失速对桨距角调节的影响

动态失速是垂直轴风力发电机在低尖速比下运行时的必然结果^[8]，是指在进口来流攻角快速变化的过程中，风轮叶片所表现出的与静态风洞实验完全不同的气动特性^[9]。

美国Sandia国家实验室测试正常工作时的垂直轴风力机，在雷诺数Re=3.6×10⁵条件下，得到了动态失速时NACA0012翼型的升阻力系数^[10]，2组结果对比如图1和图2所示。由于NACA翼型为对称翼型，其升力系数曲线关于原点对称，阻力系数曲线关于纵轴对称，故图1和图2中仅分别给出了叶片攻角大于0°时的升力系数和阻力系数。

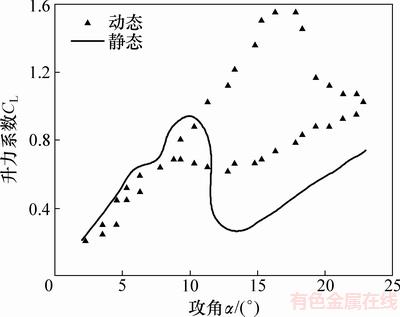
图1  升力系数对比图

Fig. 1  Comparison diagram of lift coefficient

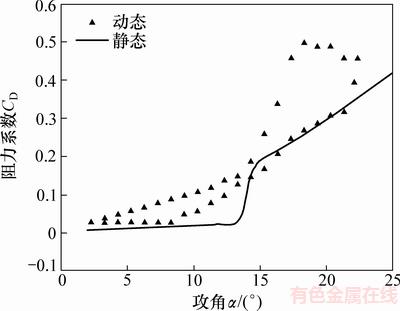
图2  阻力系数对比图

Fig. 2  Comparison of drag coefficient

从图1和图2可知：在静态条件下，当叶片攻角α=10°左右时，升力系数达到最大值。而在动态失速下所测的实验结果表明：当攻角α=17°左右时，升力系数达到最大值，风力机发生失速的攻角出现了延迟。在风力机旋转过程中，攻角最大值出现在23°左右。此后，攻角逐渐变小，按照静态风洞实验结果，在攻角变小过程中，升力系数在各个攻角处的值与攻角变大过程中的值一致。而考虑动态失速影响所测得的实验结果显示：在攻角变小过程中，升力系数变化趋势出现了明显的滞回现象；在攻角变大和攻角变小过程中，同一个攻角对应的升力系数不同，且在变大过程中升力系数较大。

同样，从图2可以看出：垂直轴风轮阻力系数由于受动态失速的影响，也发生了明显的滞回现象。在风力机旋转过程中，同一个攻角对应2个不同的阻力系数，其中，攻角变大过程中对应的阻力系数较大。对比上述2种情形可知：考虑动态失速影响所测得的翼型升力系数和阻力系数与静态条件下风洞实验结果有较大差异。所以，有必要对风轮在动态失速下的受力模型进行研究。

2  桨距角调节规律

H型垂直轴风力机属于升力型垂直轴风力发电机，风作用在叶片上产生的切向力是风轮运转的主要驱动力，它是叶片所受升力和阻力在切线方向上的合力。由翼型空气动力学可知^[11]，叶片的切向力随攻角的变化而变化，在某一攻角处切向力会达到最大值。因此，计算最大切向力所对应的叶片攻角，进而通过这个攻角调节叶片桨距角使风轮获得最大的风能利用率^[12]。

2.1  叶片理论最佳攻角计算

本文采用的1 kW H型对称翼垂直轴风轮模型如图3所示，垂直轴风轮的相关参数如表1所示，计算时雷诺数仍选为Re=3.6×10⁵。

对垂直轴风轮进行受力分解，得到作用在风轮上各力之间的关系如图4所示。图4中：W为诱导速度v和切向速度Rω的合成风速；ω为风轮旋转角速度；α为叶片攻角，即合成风速方向与叶片弦线方向的夹角；β为叶片桨距角，即切向速度方向与叶片弦线方向的夹角，可通过机构直接调节，此处β=0°；θ为叶片方位角，当方位角θ位于0°~180°时，该区域称为风轮的上风区，当θ位于180°~360°时，称为风轮的下风区；F_L和F_D分别代表叶片运动时受到的升力和阻力，将F_L和F_D沿叶片运动的切向和法向正交分解，可得到叶片受到的切向力F_T和法向力F_N，其中切向力F_T是推动风轮运转的主动力。以下讨论当升力驱动风轮产生最大切向力F_T时叶片的攻角。

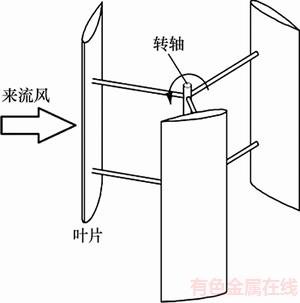
图3  H型垂直轴风力机模型

Fig. 3  Model of VAWT

表1  垂直轴风力发电机的相关参数

Table 1  Parameters of VAWT

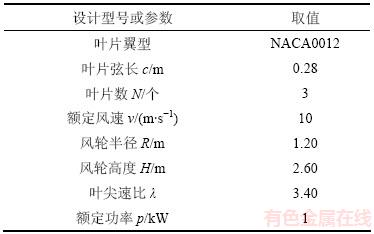
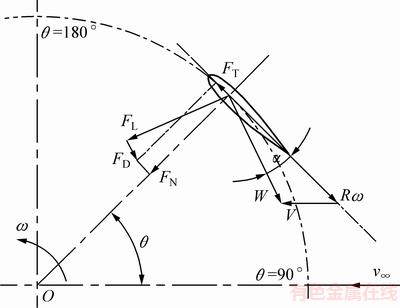
图4  叶片受力分析图

Fig. 4  Force analysis diagram of blade

以叶片在风轮上风区为例，分析图4中参数间的几何关系，可以得出垂直轴风轮叶片攻角α和合成风速W间的表达式为

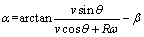          (1)

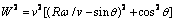       (2)

叶片所受的升力F_L和阻力F_D分别为^[12]

           (3)

如图4所示，F_L和F_D沿叶片切向运动的合力，即切向力F_T为

            (4)

式中：ρ为空气密度，在标准大气压下取1.225 5 kg/m³；c为叶片弦长；H为翼型展向的长度；C_L和C_D分别为翼型的升力系数和阻力系数，其值可由NACA系列翼型空气动力学特性数据库查得；C_T为切向力系数，是C_L和C_D在弦长方向的合成值，它们之间的关系如图5所示。

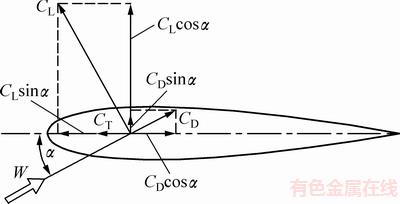
图5  叶片翼型气动力系数

Fig. 5  Aerodynamic coefficient of blade airfoil

由图5中的几何关系，得到C_T的计算式为

          (5)

由式(4)和(5)可知：要求切向力F_T，必须得到C_L和C_D。考虑到动态失速的影响，利用Sandia风力机的实验结果，并结合式(5)得到升力系数C_L、阻力系数C_D和切向力系数C_T随攻角变化的图形，如图6所示。

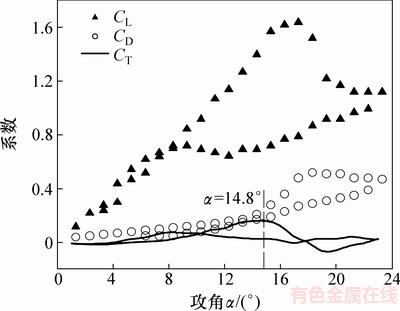
图6  动态失速下垂直轴风轮气动系数

Fig. 6  Aerodynamic coefficient of wind turbine under dynamic stall

由式(4)并结合图6中的结果可计算出驱动风轮运转的切向力F_T。风能利用率C_P为风轮的输出功率P与对应风轮的风功率P_max的比值，即

           (6)

式中：N为叶片数；S为风轮的扫掠面积。由式(6)可知：在其他参数不变情况下，当叶片攻角的取值使切向力F_T达到最大时，风能利用率C_P也为最大值。由图6可知：当攻角α=14.8°时，切向力系数C_L达到最大值，即切向力F_T达到最大值，α=14.8°就是考虑动态失速影响下叶片的最佳攻角。考虑到无论是上风区还是下风区，攻角都有逐渐变大的过程，所以，可以认为：在上风区，当攻角α=14.8°时，切向力达到最大值；同理，在下风区，当攻角α=-14.8°时，切向力达到最大值，对应的C_P也达到最大值，即风轮上风区和下风区的理论最佳攻角分别为14.8°和-14.8°。然而，目前的垂直轴风轮旋转过程中叶片攻角随方位角的变化呈类正弦规律^[13]，不能始终保持在理论最佳攻角附近，故需要对桨距角进行调节，以此维持在最佳攻角处。为使计算结果更加精确，本文结合双致动盘多流管理论对风轮桨距角的调节方法进行分析。

2.2  垂直轴风力机攻角及诱导速度计算

双致动盘多流管模型是目前研究垂直轴风力机的主要分析模型^[14]，经实验验证，该模型的计算精度较高。这里采用双致动盘多流管理论计算垂直轴风轮各个方位诱导速度，从而得到叶片攻角的实际变化情况。双致动盘多流管分析模型如图7所示。

据图7和双致动盘多流管理论，无穷远来流风v_∞流经垂直轴风轮时分为3个阶段，分别为上风区诱导速度v、转轴处的均衡诱导速度v_e和下风区诱导速度v′，其三者之间的关系为^[11]

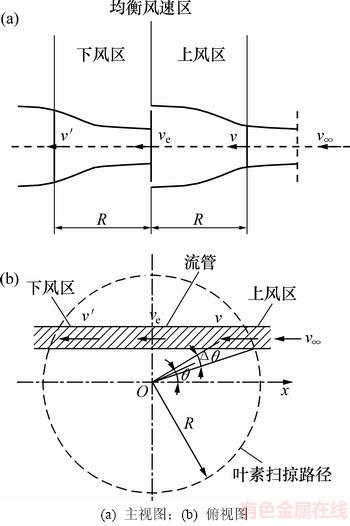
图7  双致动盘多流管理论计算模型

Fig. 7  Calculation models of multiple stream-tube and double actuator-disk theory

                 (7)

              (8)

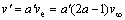          (9)

式中：a和a′分别为上风区诱导因子和下风区的诱导因子，且a＜1，a′＜1。

从方位角θ=0°开始记为第1个流管，假设模型共分为n个流管，则第i个流管的宽度为

       (10)

对每个流管进行受力分析，将流向力F_xi分解为法向力F_N和切向力F_T，得到每个流管上的流向力为

          (11)

假设风轮叶片数为N，流管总数为n，则在风轮旋转1周过程中，作用在n个流管上的平均流向力为

               (12)

对每一个流管，建立连续方程、伯努利方程和动量方程，得到作用在流管上的平均流向力F_x为

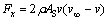             (13)

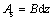                  (14)

式中：ρ为空气密度(kg/m³)；A_s为流管面积；dz为流管在竖直方向的高度。

由式(10)~(14)可得

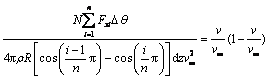 (15)

为了表达方便，将式(15)等号左边部分记为F^*，结合式(10)，则F^*为

            (16)

式(15)可以表示为

             (17)

式(17)即为风轮上风区诱导因子的迭代公式。编制Matlab程序进行计算，令诱导因子a的迭代初值为1，残差标准设置为10^-4。当诱导因子迭代计算结果收敛后，分别用式(7)计算上风区各个方位的诱导速度，用式(2)计算合成风速W，结果如图8所示。从图8可以看出：合成风速随方位角不断变化，在方位角为180°时(如图4所示)，由于切向速度的方向发生变化，合成风速的方向也发生了改变，但其大小未变。需要说明的是：上述H型垂直轴风力机的参数是在叶尖速比λ=3.40时得到的，在其他叶尖速比条件下，本文建立的双致动盘多流管分析模型同样适用。

图8  合成风速与叶片方位角的关系

Fig. 8  Relationship between resultant wind speed and azimuthal angle

2.3  桨距角调节方法

上述研究是在桨距角β=0°时进行的。根据式(1)，叶片攻角随方位角不断变化，不能保证风轮在旋转过程中保持理论最佳攻角。为提高风轮风能利用率，通过调节桨距角，达到间接改变攻角的目的。由式(1)可知叶片桨距角的表达式为

       (18)

在上风区令叶片攻角α等于14.8°，在下风区令叶片攻角α等于-14.8°，据式(18)就能得到叶片桨距角的调节规律。由于此时调节桨距角后又会对上、下风区诱导速度的分布产生影响，故需重新利用双致动盘多流管理论对调节桨距角后的模型进行迭代计算，求解新的攻角调节规律。重复此过程，直至得到的攻角与理论最佳攻角的残差小于10^-4为止，得出此时桨距角的调节规律如图9所示。

按图9所示的规律调节桨距角，得到变桨前后叶片攻角随方位角的变化规律，如图10所示。

从图10可知：叶片桨距角调节前，攻角随方位角呈类正弦规律变化，这与用矢量分析法所得的计算结果一致^[15]；叶片变桨后，风轮上、下风区叶片攻角都能够维持在最佳攻角处。

2.4  特殊方位角下桨距角调节规律修正

按此桨距角调节规律能够很好地维持叶片攻角，但是由图9可以看到，当方位角θ=0°和θ=180°时，由于风向突然改变，桨距角发生了跳变，而在实际调节过程中，这种跳变是很难实现的，因此，需要对上述桨距角调节规律进行修正。根据叶片气动性能分析结果，在当前尖速比下，当方位角θ=0°和θ=180°，且叶片受到的升力沿风轮旋转的径向时，不能当作风轮旋转推动力^[16]。所以，在方位角为0°和180°时，将桨距角调节为0°，此时攻角为0°，叶片的阻力矩最小。图11所示为修正后的叶片桨距角调节规律。

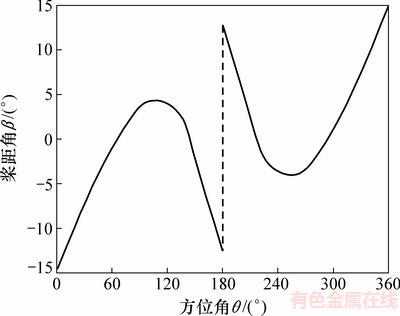
图9  叶片桨距角调节规律

Fig. 9  Adjusting rule of pitch angle

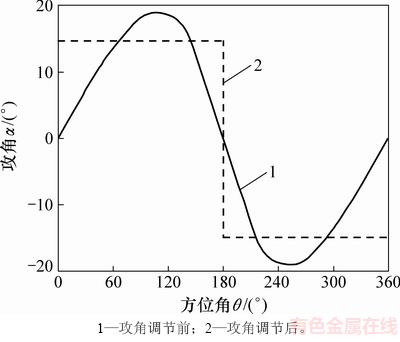
图10  调节前后叶片攻角对比

Fig. 10  Comparison of angle of attack before and after angle of attack

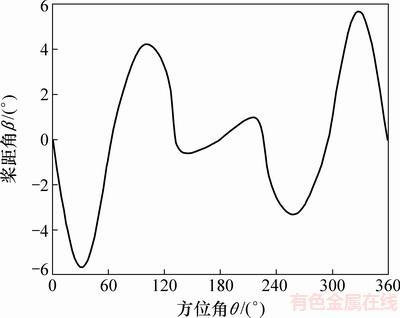
图11  修正后的叶片桨距角调节规律

Fig. 11  Revised adjusting rule of pitch angle

3  桨距角调节前后风力机性能对比

为了验证本文提出的叶片桨距角调节规律的有效性，针对本文研究的H型垂直轴风轮模型，依据表1中风力机参数，利用双致动盘多流管理论计算叶片桨距角调节前后风轮的切向力和风能利用率。

3.1  切向力对比

利用双制动盘多流管理论计算上、下风区各流管的诱导速度，利用式(4)求得变桨距前后垂直轴风轮所受的切向力如图12所示。从图12可知：叶片桨距角调节后，当60°＜θ＜150°，225°＜θ＜290°时，切向力都较之前明显增大，而在切向力小于变桨前的部分，2条曲线的差距不大。这说明这种变桨距规律能够较好地提高垂直轴风力机的切向力，进而增大风轮的转矩。

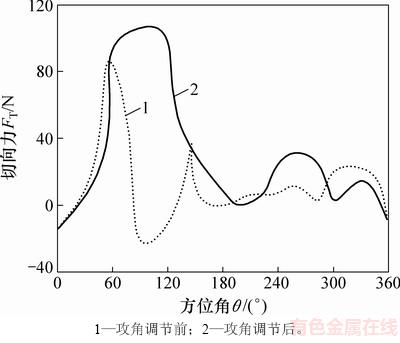
图12  变桨前后风轮所受切向力对比

Fig. 12  Contrast of tangential force before and after pitch angle adjustment

3.2  风能利用率对比

为计算风轮的风能利用率，首先求解单个叶片对风轮主轴中心的转矩T为

        (19)

N个叶片旋转1周过程中产生的平均转矩和平均输出功率分别为

              (20)

                (21)

在此基础上，风轮的风能利用率为

             (22)

式中：S为风轮扫风面积，对于垂直轴风力发电机，

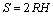               (23)

由式(19)~(23)，利用图12中切向力并结合图7中合成风速，即可计算出变桨前后垂直轴风力机的风能利用率。Matlab软件编制的计算流程如图13所示。计算结果显示：由表1中的H型定桨距垂直轴风力机计算得到的风能利用率为34.6%；而采用本文提出的变桨距方案所得风能利用率为42.8%，可见变桨效果明显。

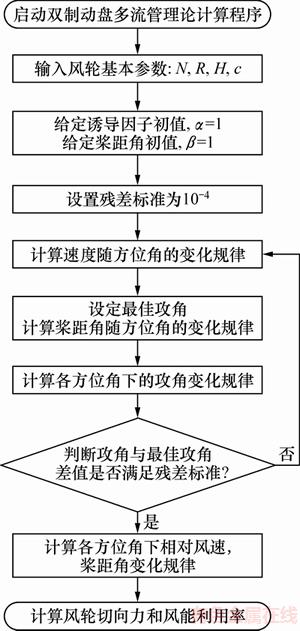
图13  双致动盘多流管理论计算流程图

Fig. 13  Calculation process under the guidance of multiple stream-tube & double actuator-disk theory

4  结论

1) 以获得最大切向力为目标，得到动态失速下本文研究的H型垂直轴风轮在上风区和下风区的理论最佳攻角分别为14.8°和-14.8°。

2) 利用双致动盘多流管理论进行Matlab编程计算，得到风轮旋转1周的变桨距规律。利用该变桨距规律，H型垂直轴风力机的风能利用率由变桨前的34.6%提高到42.8%，体现了该变桨距方法的有效性。

3) 考虑到特殊方位角下叶片升力沿风轮旋转的径向，为了减小阻力矩，规定0°和180°方位角的桨距角为0°，进一步明确了叶片变桨距变化规律。

参考文献：

[1] NOBUYUKI F, SATOSHI S. Observations of dynamic stall on Darrieus wind turbine blades[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(2): 201-204.

[2] 曹成帅, 赵允贵, 王太国. 一种新型独立变桨控制器设计[J]. 电工电气, 2016(12): 27-30.

CAO Chengshuai, ZHAO Yungui, WANG Taiguo. Design of a new type of independent variable pitch controller[J]. Electrotechnics Electric, 2016(12): 27-30.

[3] 廉正光. 采用双曲柄调距机构的垂直轴风力发电机机理研究与样机设计[J]. 机械设计, 2016, 33(8): 100-104.

LIAN Zhengguang. Principle research and prototype design of a vertical axis wind turbine with double crank adjustment mechanism[J]. Journal of Machine Design, 2016, 33(8): 100-104.

[4] 廉正光, 张宏伟, 李恺. 一种变桨距垂直轴风力发电机: 中国, 201410009955.3[P]. [2014-03-26].

LIAN Zhengguang, ZHANG Hongwei, LI Kai. A vertical axis wind turbine with variable pitch: China, 201410009955.3[P]. [2014-03-26].

[5] 赵振宙, 陈潘浩, 王同光, 等. 基于扰流技术的直叶片升力型垂直轴风轮的性能改善[J]. 机械工程学报, 2016, 52(22): 146-152.

ZHAO Zhenzhou, CHEN Fanhao, WANG Tongguang, et al. Performance improvement of lift type wind turbine with straight blades based on interference airflow technology[J]. Journal of Mechanical Engineering, 2016, 52(22): 146-152.

[6] 梁云峰, 谷凤民, 陈宇, 等. 变速恒频风力发电机组液压变桨距系统的设计与仿真[J]. 机床与液压, 2017, 45(2): 63-68.

LIANG Yunfeng, GU Fengmin, CHEN Yu, et al. Design and simulation for hydraulic variable pitch system of wind turbine with variable speed and constant frequency[J]. Machine Tool & Hydraulics, 2017, 45(2): 63-68.

[7] SHELDAHL R E. Aerodynamic characteristics of seven airfoil sections through 180 degrees angle of attack for use in aerodynamic analysis of vertical axis wind turbines[R]. Sandia: Sandia National Laboratories, 1981: 12-40.

[8] NOBUYUKI F, SATOSHI S. Observations of dynamic stall on Darrieus wind turbine blades[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(2): 201-214.

[9] 查顾兵. 风力机动态失速模型的研究及其在性能预测中的应用[D]. 上海: 上海交通大学机械与动力工程学院, 2009: 37-46.

ZHA Gubing. Research and application of dynamical stall model in wind turbine[D]. Shanghai: Shanghai Jiaotong University. School of Mechanical Engineering, 2009: 37-46.

[10] ALLET A, PARASCHIVOIU I. Viscous flow and dynamic stall effects on vertical-axis wind turbines[J]. International Journal of Rotating Machinery, 1995, 2(1): 1-14.

[11] 伊恩·帕拉斯基沃尤. 垂直轴风力机原理与设计[M]. 李春, 叶舟, 高伟, 译. 上海: 上海科学技术出版社, 2013: 62-86.

PARASCHIVOIU I. Principle and design of vertical axis wind turbine[M]. LI Chun, YE Zhou, GAO Wei, trans. Shanghai: Shanghai Science and Technology Press, 2013: 62-86.

[12] CHOUGULE P, NIELSEN S. Overview and design of self-acting pitch control mechanism for vertical axis wind turbine using multi body simulation approach[C]//The Science of Making Torque from Wind. Lyngby, Denmark, 2014: 1-10.

[13] 张立军, 刘华, 赵昕辉, 等. 垂直轴风力机非对称翼型叶片变攻角方法[J]. 可再生能源, 2016, 34(2): 232-237.

ZHANG Lijun, LIU Hua, ZHAO Xinhui, et al. The method for wind turbine to vary angle of attack of asymmetric airfoil blade[J]. Renewable Energy Resources, 2016, 34(2): 232-237.

[14] BLUSSEAU P, PATEL M H. Gyroscopic effects on a large vertical axis wind turbine mounted on a floating structure[J]. Renewable Energy, 2012, 46(5): 31-42.

[15] 张立军, 刘华, 赵昕辉, 等. 垂直轴风力机非对称翼型叶片变攻角方法[J]. 可再生能源, 2016, 34(2): 232-237.

ZHANG Lijun, LIU Hua, ZHAO Xinhui, et al. The method for wind turbine to vary angle of attack of asymmetric airfoil blade[J]. Renewable Energy Resources, 2016, 34(2): 232-237.

[16] KIRKE B K, LAZAUSKAS L. Limitations of fixed pitch Darrieus hydrokinetic turbines and the challenge of variable pitch[J]. Renewable Energy, 2011, 36(3): 893-897.

(编辑  陈灿华)

收稿日期：2017-11-18；修回日期：2018-01-12

基金项目(Foundation item)：山东省自然科学基金资助项目(ZR2014EEP022)；中央高校基本科研业务专项资金资助项目(17CX05021)(Project (ZR2014EEP022) supported by Natural Science Foundation of Shandong Province; Project(17CX05021) supported by the Fundamental Research Funds for the Central Universities)

通信作者：张立军，博士，教授，硕士生导师，从事可再生能源技术和绿色装备制造研究；E-mail：zhanglijun@upc.edu.cn