J. Cent. South Univ. (2020) 27: 432-448

DOI: https://doi.org/10.1007/s11771-020-4307-0

Cooperative task allocation for heterogeneous multi-UAV using multi-objective optimization algorithm

WANG Jian-feng(王建峰), JIA Gao-wei(贾高伟), LIN Jun-can(林君灿), HOU Zhong-xi(侯中喜)

College of Aerospace Science and Engineering, National University of Defense Technology,Changsha 410073, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: The application of multiple UAVs in complicated tasks has been widely explored in recent years. Due to the advantages of flexibility, cheapness and consistence, the performance of heterogeneous multi-UAVs with proper cooperative task allocation is superior to over the single UAV. Accordingly, several constraints should be satisfied to realize the efficient cooperation, such as special time-window, variant equipment, specified execution sequence. Hence, a proper task allocation in UAVs is the crucial point for the final success. The task allocation problem of the heterogeneous UAVs can be formulated as a multi-objective optimization problem coupled with the UAV dynamics. To this end, a multi-layer encoding strategy and a constraint scheduling method are designed to handle the critical logical and physical constraints. In addition, four optimization objectives: completion time, target reward, UAV damage, and total range, are introduced to evaluate various allocation plans. Subsequently, to efficiently solve the multi-objective optimization problem, an improved multi-objective quantum-behaved particle swarm optimization (IMOQPSO) algorithm is proposed. During this algorithm, a modified solution evaluation method is designed to guide algorithmic evolution; both the convergence and distribution of particles are considered comprehensively; and boundary solutions which may produce some special allocation plans are preserved. Moreover, adaptive parameter control and mixed update mechanism are also introduced in this algorithm. Finally, both the proposed model and algorithm are verified by simulation experiments.

Key words: unmanned aerial vehicles; cooperative task allocation; heterogeneous; constraint; multi-objective optimization; solution evaluation method Cite this article as: WANG Jian-feng, JIA Gao-wei, LIN Jun-can, HOU Zhong-xi. Cooperative task allocation for heterogeneous multi-UAV using multi-objective optimization algorithm [J]. Journal of Central South University, 2020, 27(2): 432-448. DOI: https://doi.org/10.1007/s11771-020-4307-0.

1 Introduction

Unmanned aerial vehicles (UAV) are widely used in the suppression of enemy air defense (SEAD) missions since it has high viability, low cost, flexible features [1]. However, with the increasingly complex application environments and sophisticated mission requirements, individual UAV is not enough, and a UAVs team is required. Thus, the heterogeneous UAVs refers to UAVs with different operational capabilities [2]. It is widely accepted that a proper allocation plan can lead the heterogeneous UAVs to perform a variety of tasks flexibly. Task allocation has an extraordinary significance in the application of the multi-UAV system [3]. The key issue of cooperative task allocation is to allocate necessary tasks and schedule the task execution sequence to get a satisfactory performance [4]. Theoretically, Task allocation problem is a combinatorial optimization problem containing various contradictory optimization objectives, and it’s also a typical NP-hard problem [5]. There are two difficult points in the problem: problem modeling and model solving.

As for the modeling, the cooperative multiple task allocation problem (CMTAP) [6] is usually formulated as the traveling salesperson problem [4, 7] or vehicle routing problem [8]. The Dubins vehicle method is usually introduced to reflect UAV basic dynamics constraints [9, 10]. In this paper, the following characters should be fully considered during the realistic CMTAP for heterogeneous UAVs, i.e., task coupling, time constraint and heterogeneity.

Firstly, the coupled task should be considered. The assignment of UAVs for independent tasks has been widely studied, such as reconnaissance [4, 11], attack operation [2], farmland operation [3] and other independent tasks [12, 13]. However, tasks are coupled and need be performed sequentially in the SEAD operation, e.g., reconnaissance, attack, and verification [14]. Secondly, the time window needs to be considered at some time-critical targets [13, 15, 16], namely, a target is expected to appear in a limited period. Thirdly, the heterogeneity of the UAV platform should be treated specially. The operational capabilities of UAVs may not be isomorphic, since different types of aircrafts (fixed-wing, rotor) have specific kinematic characteristics (minimum turning radius, reconnaissance range and speed) [11]. With limited and unequal resources (ammunition), the cooperation of heterogeneous formation is applicable to distinct tasks. Finally, the economic cost of the allocation plan should be considered, e.g., the cost of UAVs, the damage of targets and the task reward.

Generally, there are two categories of solving methods: traditional methods and intelligent optimization methods. Through the traditional methods, such as dynamic programming [16], mixed integer linear problem method (MILP) [17, 18], optimal solutions can be obtained, while large-scale allocation problems cannot be solved efficiently. For the task allocation problem, an optimal solution is difficult to be obtained within the reasonable time by the traditional method. To obtain approximate solutions with less computational time, intelligent optimization algorithms have been widely applied [19], such as particle swarm optimization (PSO) [3, 15, 20], ant colony algorithm [21], evolutionary algorithm (NSGA-II) [1, 22], simulated annealing algorithm. These methods are more efficient than traditional algorithms since substantial gradient information is not required. However, the solution space expands exponentially with the scale of the UAVs, targets and optimization objectives increases, which puts forward higher requirements for algorithm efficiency. Quantum-behaved particle swarm optimization (QPSO), a new variant of PSO, has stronger global search capabilities and fewer control parameters than the original PSO [19, 23].

In this paper, a modified model is established to describe the cooperative task assignment problem for heterogeneous UAVs in the SEAD operation. More detailed constraints are contained in the model for UAVs and tasks based on the three attributes (task coupling, time constraint and heterogeneity). A constraint scheduling method is designed to handle the critical logical and physical constraints if the feasibility of plan is limited by certain constraints. Subsequently, an improved multi-objective quantum-behaved particle swarm optimization (IMOQPSO) algorithm is proposed to solve the model efficiently. A comprehensive evaluation method is added to evaluate the solutions, so as to increase the selection pressure during updating. Based on the evaluation results, each particle can be adaptively adjusted to improve the search performance.

The rest of this paper is organized as follows. In Section 2, the task scenario, the basic model (target, task and UAV), optimization objectives and constraints are defined. In Section 3, multi-objective optimization algorithm is improved from three perspectives: solution evaluation method, adaptive control factor, and mixed search mechanism. In Section 4, the simulation and result are explained, including the analysis of allocation plans and the validation of the feasibility of the optimization method. The conclusions are drawn in the last section.

2 Task allocation model for heterogeneous UAVs

2.1 Scenario description

In the SEAD operation, multiple tasks need to be performed based on each target, e.g., reconnaissance, classification, attack, and verification. A variety of different equipment is required in these operations, and if all the equipment is mounted on a single UAV, it will be a huge challenge due to its limited payload. Heterogeneous UAVs with different equipment can satisfy this kind of requirement, and perform complex tasks through effective cooperation among UAVs. Accordingly, the following preconditions are established to analyze the cooperation task allocation problem:

1) Targets are static with known locations. The operating area is simplified to a two-dimensional area.

2) UAVs have limited range and resource on board. The attack task is performed by the ammunition unit carried by the UAV. Different types of UAVs work at different altitudes.

3) Time-window constraints need to be considered in the task execution.

It is noted that the task allocation can be divided into two types: the centralized allocation method and the distributed allocation method [24]. The centralized allocation method can reflect global characteristics and is suitable for strongly coupled task allocation problems. Thus, the centralized allocation strategy is adopted in this paper.

2.2 Basic model definition

In this section, four basic models are defined: target model, task model, heterogeneous UAV model and path planning model.

2.2.1 Modeling of target and task

Stationary targets in the SEAD operation are mainly studied in this paper. Figure 1 shows the schematic of the task allocation in the operation. There are N_T targets with known location information. Each target T_i, i=(1, 2, …, N_T) contains three types of tasks (N_type=3): reconnaissance, attack and verification. Three tasks of the same target need to be performed sequentially. The target can only be attacked after being reconnoitered, and the verification task needs to be performed to evaluate the status of targets after completing the attack task. The time intervals between these consecutive tasks are represented by parameter Δt_w.

In the operation, M_k, k={1, 2, …, N_M}, represents the k-th task, in which N_M=N_TN_type represents the total number of tasks. In order to describe the relationship between tasks and targets, the correlation coefficient C_ik is proposed in the model. If task M_k belongs to target T_i, then C_ik=1; otherwise, C_ik=0.

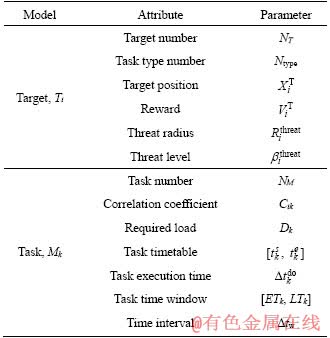
Table 1 shows detailed attributes of targets and tasks. For the target,denotes the location of the target; 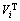represents the reward for completing all tasks of the target; 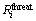denotes the threat radius of the target;is the probable damage caused by the target to UAVs.

For the task, D_k indicates the task resources requirement;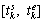represents the task timetable; 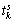and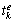denotes the start time and completion time, respectively;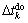indicates the task execution time, and it is related to UAV type and task type; 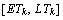indicates the time window constraint; ET_k is the earliest allowed execution time of the task; and LT_k is the latest allowed completion time.

2.2.2 Modeling of heterogeneous UAV

There are N_V UAVs in the heterogeneous multi-UAV system. U_j, j={1, 2, …, N_V}, denotes the j-th UAV. Three types of UAVs are applied in the operation: reconnaissance UAV, attack UAV and integrated UAV. The differences between heterogeneous UAVs are mainly characterized in operational capabilities and kinematic constraints.

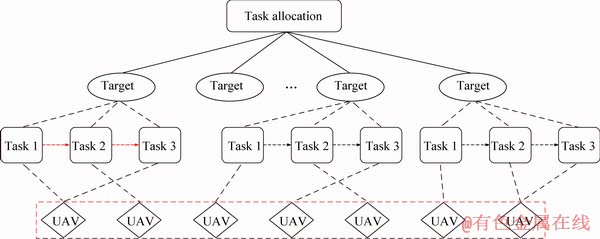
Figure 1 Schematic of targets and tasks

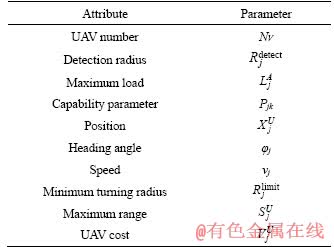
Table 1 Attributes of target and task

In terms of the operational capability, reconnaissance UAV is equipped with the information reconnaissance equipment, which can perform reconnaissance task and verification task. Attack UAV is equipped with limited ammunition unit, which is responsible for attack task. Integrated UAV can perform reconnaissance, attack and verification tasks omnipotently. is introduced to describe the detection radius of the onboard sensor. The number of ammunition units is limited by the maximum load 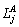of UAV. Furthermore, the capability parameter 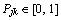is proposed to describe the task ability, and it represents the performing ability of UAV U_j to task M_k.

The dynamic model U_DM of the UAV is as follows [4]:

               (1)

where 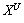represents the UAV position; φ represents the heading angle; v denotes the speed; R^limit represents the minimum turning radius; S^U denotes the maximum range.

Table 2 shows attributes of these UAVs.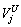represents the cost of UAV, and it is introduced to describe the economy of the allocation plan. For example, the integrated UAV has a higher cost than the other two types of UAVs, so it is uneconomical to assign the integrated UAV to perform high-risk tasks.

Based on the UAV model and task model, the allocation parameter X_jk is proposed to describe the relationship between UAVs and tasks. The parameter is defined as follows:

         (2)

Table 2 Attributes of UAV model

2.2.3 Modeling of path planning

The transfer time and task execution time can be calculated in path planning model based on the UAV dynamic attributes. The standard Dubins method is widely used in path planning by simplifying the dynamics of UAVs. It consists of four elements: starting waypoint, starting heading, terminal waypoint and terminal heading [25]. The distribution relationship between the UAV and the target should be considered in the task allocation problem, so as to determine the start waypoint and terminal waypoint of the path. Dubins method with terminal heading relaxation is introduced for calculation. In other words, the terminal heading is not pre-specified, and it is related to the shortest transfer track.

In the calculation, 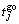indicates the take-off time of the UAV;is defined as the transfer time from the previous task to the next task M_k;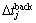 represents the returning time of UAV to the take-off base after completing all tasks. In the path planning, the following settings are created:

The detection radius of the UAV is greater than the threat radius of the target, and the threat radiusis greater than the minimum turning radius.

       (3)

When performing the reconnaissance or verification tasks, UAV is considered to complete the task after hovering around the target with the detection radius of 3/4 circle. In practice, it is generally believed that 3/4 circle is sufficient to get the information. The hovering time of the UAV is taken as the execution time.

The trajectories of UAVs are related to task types. The trajectory calculation rules are as follows:

1) Reconnaissance or verification task: Find the shortest flight path from the starting point to the circular reconnaissance track (the target position is the center, and detection distance is the radius). The angle of entry into the track is related to the shortest Dubins path.

2) Attack task. The target position serves as the next waypoint for the UAV. The heading of the UAV is not constrained when the target is achieved.

3) When the UAV completes a mission, the current heading angle is the starting heading angle of the next trajectory.

4) The initial heading angle of the drone is preset. UAVs return to the take-off base after finishing tasks.

Figure 2 shows a schematic diagram of the path planning, including two UAVs (an attack UAV at point A and a reconnaissance UAV at point F), and two targets (T₁ at points C and T₂ at point E). R₁ is the turning radius of the attack UAV (black dotted circle O₁); R₂ is the turning radius of the reconnaissance UAV (brown dotted circle O₂); R₃ is the detection radius (green dotted circle); R₄ and R₅ denote the threat radius of the target T₁ and T₂, respectively (two red dotted circles, the center of circle represents the target position).

The red line indicates the trajectory of the attacking UAV: after the UAV completes the attack mission to the target T₁ (arc AB and line BC), the current heading angle is used as the starting heading angle of the next mission, and Dubins method is used to calculate the path to the T₂ target point (arc CD and line DE). The blue line represents the trajectory of the reconnaissance UAV. The UAV first enters the hover reconnaissance mission in the circular route centered on the target T₁. After hovering 3/4 circle (arc HI), the heading angle at I is the current heading angle, planning to the route at T₂.

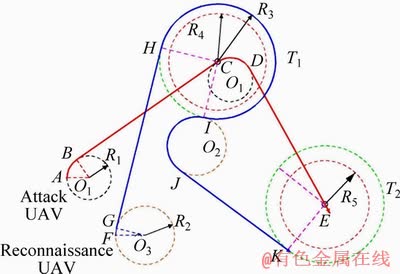
Figure 2 Dubins paths of UAVs

2.3 Formulation of optimization problem

Based on the four basic models, model constraints and optimization objectives are formulated in this section.

2.3.1 Mathematical constraint

All the constraint can be divided into two parts: physical constraint and logical constraint. Physical constraints are generated from capability limitations of the UAV, such as the allocated constraint, capacity constraint, load constraint and range constraint. Logical constraints are related to the requirements of the task, such as time-window constraint and dependency constraint.

Allocated constraint: in the operation, each task needs to be performed by one UAV, but each UAV can perform many tasks if it has quality and resource.

                    (4)

Capacity constraint: the selected UAV must match its tasks. The quality parameter Q_k is defined to assess the quality of task execution. If Q_k=0, it indicates that the task M_k is not performed correctly.

                (5)

Load constraint: The resources spent by UAV cannot exceed its own load limit:

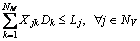                    (6)

Range constraint: The flying distance of each UAV should be less than its range.

     (7)

Time-window constraint: Some tasks need to be executed in a specific time window. If the constraint is violated, the targets may be lost, and the survival probability of UAV is reduced.

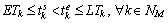                (8)

Dependency constraint: Execution sequence and task interval need to be considered when there is a coupling relationship between tasks. This constraint will be analyzed in detail during the task scheduling process in the next section.

2.3.2 Mathematical optimization objective

Four optimization objectives are defined in the task allocation model to evaluate various allocation plans: completion time, task reward, UAV damage, and total range.

Completion time (makespan) objective: The completion time is widely used as an optimization function. Most decision-makers aim to find a plan to complete the mission as soon as possible under the constraint conditions [3, 22].

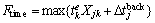                  (9)

Reward objective: The reward objective is introduced to ensure that high-value tasks can be assigned to a UAV with a higher success rate. The reward objective is calculated by Eq. (10). Rather than calculating the individual benefits of each task, the computation of reward calculates the overall benefits of UAV group performing the tasks of the same target. In order to minimize all optimization objectives, the reward optimization function is set to the target’s lost value. The lower the value of the reward objective, the better the task completion.

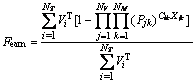             (10)

Damage objective: The damage objective is defined to assess the threat of targets to UAVs. In the SEAD operation, the target is harmful to UAVs, so high-value drones need be selected carefully. So, UAV damage objectives are proposed to evaluate the risk of the mission. The objective is related to the cost of the UAV and the threat level of the target. The objective is calculated by Eq. (11), in which f(C_TW) is the time-window indicator. If the task violates the time-window constraint f(C_TW)=1; otherwise, f(C_TW)=0.

   (11)

Total range objective: The total range is used to assess the economy of the plan [3]. The range is directly proportional to its energy consumption and equipment loss. The total range of UAV is taken as an optimization objective, so that task allocation plan can be evaluated more accurately. The range function is given by Eq. (12):

       (12)

In summary, the heterogeneous UAV cooperative task allocation model is as follows:

               (13)

2.4 Task scheduling

In this section, a task scheduling method is described to obtain feasible solutions that satisfy all constraints.

2.4.1 Task scheduling framework

The allocation plan contains two parts: task assignment and time schedule. Task assignment focuses on the relationship between tasks and suitable UAVs. Time schedule contains the timetable for each task, take-off time and landing time of UAV. In the calculation, the generated initial solution may violate certain constraints. The illegal solutions need to be adjusted in three parts: task sequence, selected UAV and task schedule. Figure 3 shows the task scheduling process and the corresponding constraints.

The initial solution contains two parts: a task list and the selected UAV. In the SEAD operations,tasks are interrelated rather than isolated. All tasks must be performed in the prescribed order. The task relationship matrix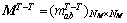is proposed to describe the coupling relationship. If task M_a must be completed before task M_b, then ; otherwise, The task sequence needs to be adjusted according to the task relationship matrix. The corresponding UAV moves with the task when adjusting the sequence. The pseudo code of the task sequence adjustment is as follows:

Algorithm 1: Task sequence adjustment

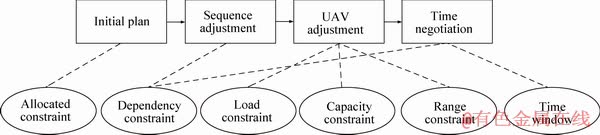
Figure 3 Task scheduling process and constraint handling

2.4.2 UAV adjustment and time negotiation

After adjusting the task sequence, UAVs which do not meet the requirements will be adjusted. The selected probability PS_jk that the UAV U_j is allocated to the task M_k is calculated by the available resources 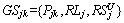and task demand where P_jk is the capability; RL_j is the remaining load; 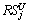is the remaining range; DP_k is the demand probability; DL_k is the demand loads; DS_k is the demand ranges; NS_j is the number of tasks that have been assigned to the UAV. The selected probability is calculated by Eqs. (14) and (15).

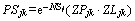                   (14)

                  (15)

The demand range DS_k is related to the UAV position and mission status. Due to the coordination relationship between tasks, after the UAV reaches the target, the pre-order task may not be completed or the time window is not satisfied. Then, UAV needs to hover and wait, which increases the range requirements. The demand range is calculated by Eq. (16), where 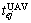is the completion time of the previous task performed by the selected UAV. if the UAV performs the task for the first time.

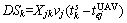                     (16)

The purpose of time negotiation is to coordinate the time schedule. The adjusted task sequence satisfies the coupling relationship. The time negotiation mainly calculates the start time, end time of the task and the departure time of the UAV. The task M_a will be taken as an example for calculation. Its start time is calculated by the Eq. (17). 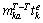indicates the completion time of the task with the higher priority higher than M_a. The start time needs to meet the UAV’s own dynamic constraints, task dependency constraint and time window constraints. The departure time of the UAV U_j is defined by Eqs. (17) and (18).

    (17)

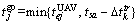                   (18)

If the start time or demand range cannot satisfy Eqs. (19) and (20). The UAV needs to be re-selected.

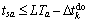                          (19)

                     (20)

2.4.3 Complete scheduling process

The pseudo code of the task scheduling:

Algorithm 2: Task scheduling

3 Method for multi-objective optimization

To efficiently solve this problem, the details of particle coding and the improved algorithms are described in this section.

3.1 Multi-layer encoding

The proposed coding method is derived from the idea of multi-layer encoding in the genetic algorithm. A real-number encoding method is used to establish the mapping between the particle and the actual problem. Real-number coding is most useful for function optimization problems, and it is convenient for the crossover mutation operation.

The allocation plan is generated by simple decoding. The particle dimension is the same as the total number of tasks to ensure that each task is assigned to a single UAV. The particle position X is divided into the integer part and the decimal part. The integer part [X] represents the serial number of the selected UAV. The decimal part {X} is used to generate the task sequence according to the initial sequence. Figure 4 shows an example of the decoding process in operation, which describes the allocation of four UAVs and two targets.

The establishment of the task sequence is the core of the particle decoding process, and the blue dashed box portion in Figure 4 shows the task sequence generation process. The initial sequence is generated in ascending order of the target number. Since each target has 3 coupled tasks, targets 1 and 2 appear three times in the initial sequence. The sorted decimal part is generated by arranging the decimal parts of the particles in ascending order. A correspondence can be established by the sorted decimal part and the initial sequence. Based on this correspondence, the new task sequence can be generated by the original decimal part (not sorted). The distinction of multiple tasks of the same target is discriminated by the order in which the tasks appear. As shown by the red number in Figure 4, the first one is the reconnaissance task; the second is the attack task, etc.

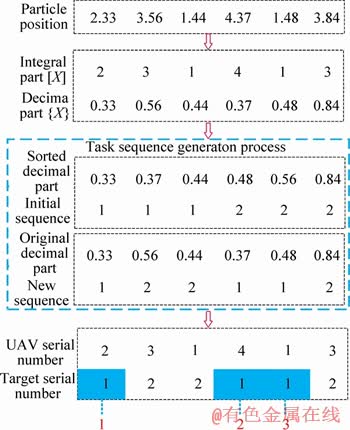
Figure 4 Particle decoding schematic

3.2 Improved optimization algorithm

3.2.1 Mixed search strategy

The improved algorithm is based on the quantum particle swarm optimization algorithm, blending with the crossover and mutation operations.

The quantum-behaved particle swarm update strategy is the main body update mechanism. The selection of global optimal points has a great influence on the computational results. Particles in the external repository with higher evaluation function values (top 10%) are selected to guide the evolution of the algorithm. The particles in QPSO evolve as follow:

    (21)

where x_ij(t) represents the position of t-th generation. i (i=1, 2, …, m) denotes the i-th particle of the population, andis the population size. j (j=1, 2, …, n) represents the j-th dimension of the particle, and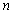is the particle dimension. p_ij(t) is local attractor. β denotes the contraction-expansion factor. c_j(t) represents the average best location.u_ij(t) and φ_i(t) are random numbers in the range of [0, 1]. y_ij(t) and 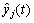represent the best previous position and the global best position respectively.

Another search mechanism is used in the external repository to enhance the diversity of non-dominated solutions and avoid trapping into a locally optimal solution. The crossover strategy is adopted. After the particle is decoded, it can be equivalent to a chromosome. Figure 5 is a schematic diagram of the crossover operation. A pair of chromosomes is randomly selected from the population and repository respectively. In this way, information exchange between the repository and the population can be promoted. The new location of the selected particle is calculated by using the following equation:

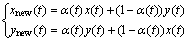            (22)

where t represents the location of chromosomes. 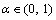is the random variable with the same chromosome length. Single point mutation method is adopted in the algorithm. The mutation operator randomly selects the mutant individuals from the population first and then selects the mutation positions. New values are generated within the mutation range to replace the selected locations. Crossover and mutation operations only change the allocation of UAVs and the order of tasks.

3.2.2 Solution evaluation method

Bi-objective problems are common in the multi-objective optimization problems, and more optimization objectives will reduce the selection pressure of Pareto dominance. Hence, a modified solution evaluation method is designed to keep reservations for promising solutions effectively.

Our allocation problem doesn’t have the prior knowledge. If algorithm focuses on the convergence only, particles will be crowded around the ideal point (Z=(0, 0, …, 0)). Besides, if it focuses on the distribution, the final solutions will be loosely distributed and away from the front [26, 27]. Accordingly, the evaluation method focuses on the convergence state and distribution state synthetically.

The calculation contains four main parameters: convergence parameter C_v, projection parameter C_p1, vertical projection parameter C_p2 and distributed parameter C_d. Based on these parameters, particles will be divided into certain area with different priority. The evaluation value g(x) is established by Eq. (23). λ denotes the distribution coefficient. δ represents the weight coefficient for reward or punishment. The higher the evaluation value, the better the performance of the solution.

                 (23)

Convergence parameter C_v: it is calculated by measuring the distance between the particle and the ideal point in Eq. (24).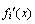,i={1, 2, …, m}, represents the normalized objectives and ranges from [0, 1].

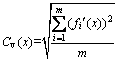                      (24)

Parameter C_v is somewhat unfair for the special boundary solutions. C_p1 and C_p2 are used to compensate for the lack of the traditional convergence parameter in BFE method [26]. C_p1 is the projection of the particle convergence parameter to the reference line (Figure 6 shows the line connecting ideal point Z to worst point Z_w=(1, 1, …, 1)). C_p2 represents the vertical distance. These two parameters will be used as the basis for judging the boundary solutions.

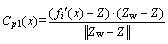               (25)

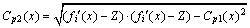    (26)

The averages of three parameters: meanC_v, meanC_p1 and meanC_p2. Based on the six parameters, the solution space can be partitioned. Figure 6 shows a schematic. The space is divided into four parts: areas A, B, C, and others.

Figure 5 A sample of crossover operation

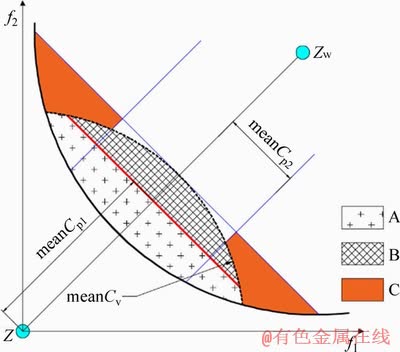
Figure 6 Particle partitioning schematic for bi-objective

1) Area A: C_vv, C_p1p1. The particles in this region are closer to the Pareto front, which is the best convergence region in the evolution of the algorithm.

2) Area B: C_vv, C_p1>meanC_p1. The convergence performance of this region is slightly poor, which is not effective for promoting algorithm evolution.

3) Area C: C_v>meanC_v, C_p1v, C_p2> meanC_p2. The boundary solutions are mainly distributed in this area, which should be retained to increase the diversity of the allocation plans.

4) The particles in the remaining regions are not of high evolutionary value and are not grouped in detail.

Distribution parameter C_d: The shift-based density estimation [28] (SDE) method is used to assess the distribution. It is calculated by Eqs. (27)- (29). The SDE distance is an index to measure the spatial distribution of solutions. And it has lower computational complexity than other method, such as the crowded distance, grid dominance [29], destiny estimator [30], etc. sde denotes the distance of the j-th solution in the i-th normalized objective. In Eq. (29): in the i-th objective dimension, take x_a and x_b as examples, when a is greater than b, c is 4; otherwise, it is 0. In the i-th optimization objective dimension, take a and b as an example. When f ′_i(x_a) is greater than f ′_i(x_b), sdei_ab is f ′_i(x_a)-f ′_i(x_b); otherwise, it is 0. The larger the SDE value, the further the particle is from surrounding particles. meanC_d is the average of parameter C_d. Distribution states: sparse C_d>meanC_d, crowded C_dd.

                   (27)

                   (28)

        (29)

Without the loss of generality, the setting of the coefficients in Eq. (23) is as follow. In area A, coefficient δ=1 is set to retain particles in the area. In area B, coefficient δ=0.8 is set to punish particles in this area slightly. In area C, δ=1.2 is set to reward some solutions of the boundary. In other area δ=0.2 is set to discard the solution in this area. The distribution coefficient λ is calculated by Eq. (30). When the particles are in a crowded state, the parameters of the region are preserved by randomly setting.

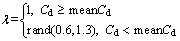             (30)

If particles in the external repository exceed their prescribed scale, all non-dominated solutions will be sorted according to the evaluation value, and the solutions with low evaluation value will be removed.

3.2.3 Adaptive control factor

In QPSO, there is a single contraction- expansion factor β to balance the local and global search during the search process. β<1.781 should be set to guarantee convergence of the particle [31]. If the factor is too large, there is a strong global search ability of the algorithm; if the factor is too small, there is a strong local search ability. The actual search process is non-linear and highly complex, and the factor has a great influence on the efficiency of the algorithm.

In order to improve the accuracy of evolution, the contraction-expansion factor of each particle is dynamically set according to its evaluation function. The control factor is divided into two factors: the evolutionary factor s_d and the aggregation factor j_d.

The evolutionary factor s_d is defined as follow, where The larger the evolutionary factor, the better the performance of the particle, and the local search ability can be enhanced.

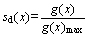                          (31)

The aggregation factor j_d is defined as follows, where 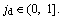The larger the aggregation factor, the higher the degree of particle aggregation, and the global search ability can be enhanced.

                           (32)

The adaptive contraction-expansion factor is defined by Eq. (33). For each particle, it is possible to set a contraction-expansion factor which is suitable for its state, thereby the efficiency of the algorithm is improved, so the algorithm parameters are set as follows:

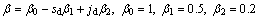   (33)

3.2.4 Complete algorithm framework

Based on the improved algorithm, detailed steps to solve the task allocation problem are presented as follows:

Step 1: Set algorithm parameters and initialize the population and the external repository.

Step 2: Perform task scheduling operation for the particles according to contents of Section 2.4, and calculate the optimization objectives.

Step 3: Calculate the evaluation function value and the adaptive control parameter of the particle according to its optimization function values.

Step 4: Fill the external repository according to the dominant relationship, and use the evaluation function to maintain the size of the repository.

Step 5: Select global best particles with higher evaluation function values (top 10%) from the external repository.

Step 6: Update the particles in the population according to the quantum behavior particle swarm algorithm mechanism. Some particles in external repositories are selected to update through the mixed update mechanism.

Step 7: Determine whether the termination condition (maximum iteration) is satisfied or not. If not, skip to step 2 and cycle until the final condition is satisfied.

Figure 7 shows the process of solving the issue.

4 Simulations and results

The implementation of anti-radar operations by heterogeneous multi-UAV systems is a vital combat style for the SEAD operation, and it has received extensive attention. The anti-radar operation will be discussed as a typical application scenario for heterogeneous UAVs in the simulation.

There are six targets and nine UAVs in the simulation. Multiple solutions are generated by various optimization algorithms. By comparing the non-dominated solutions, it is proved that the proposed IMOQPSO algorithm can efficiently solve the task allocation problem of heterogeneous UAVs. The simulation environment is an Intel (R) Core i5-3470 CPU with 8 GB RAM.

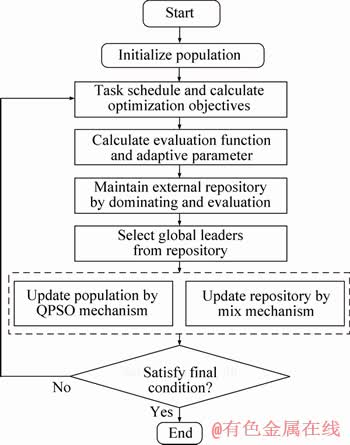
Figure 7 Flowchart of improved algorithm

4.1 Simulation statement

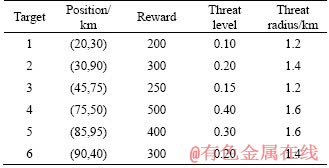
In order to conform to the actual situation, the total coverage of the operation area is 10000 km², representing by the coordinate (0, 100) in the x-axis and (0, 100) in the y-axis, respectively. The positions of the targets are simplified to point representation. Table 3 lists the details of targets.

Table 3 Detail of targets with required load of 1

The time window of the attack task is set for each target, and a certain time interval is also set between attack and verification missions. Table 4 shows the time window for the presupposed targets. For example, the attack mission for the target 1 should satisfy the time window [30, 90] min. In addition, there must be at least a 5-min interval between verification task and attack task to avoid the smoke and dust interference caused by the attack task.

Table 4 Task time window

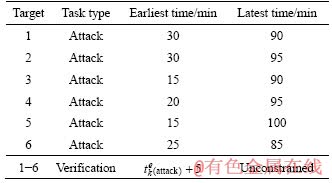
Figure 8 shows the initial positions of the UAVs and targets. The six targets are marked by the red triangles, and the take-off positions of UAVs are marked by the blue diamonds.

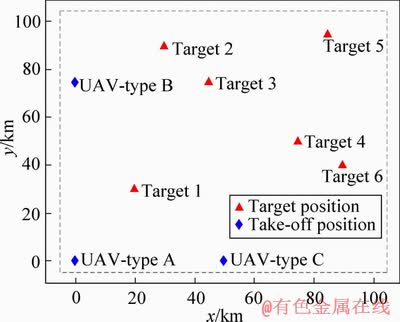
Figure 8 Scenario configuration-initial positions of target and UAV

In the simulation, nine UAVs are arranged to perform these tasks. UAVs 1-3 are reconnaissance UAVs (Type A). UAVs 4-6 are attack UAV (Type B). UAVs 7-9 are integrated UAVs (Type C).Table 5 indicates the necessary information about the three types of UAVs. UAVs are limited by range and load, and can perform limited tasks.

4.2 Allocation plans and analysis

Table 6 shows the details of the optimization objectives for four representational allocation plans. The details of the task assignment and task schedule are shown by Gantt charts.

Table 5 Basic information about UAVs

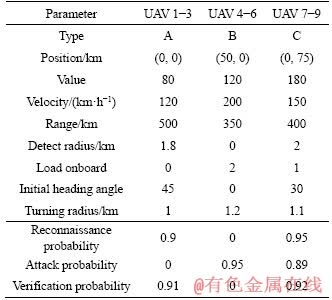
Table 6 Alternative solutions

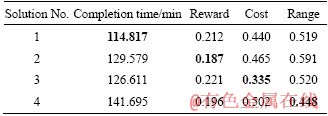
In these Gantt charts, M in M0N represents the target number; 0N is the mission number. 01 represents reconnaissance task; 02 represents the attack task; 03 represents the verification task. Then Gantt charts are analyzed and compared in the following part as shown in Figures 9-12.

Solution 1 has the shortest completion time. Most of the missions are coordinated by two or three UAVs to reduce the makespan maximally. In task assignment, UAVs with higher speeds are more popular (types B and C). The average number of tasks, for type A is 2; type B is 1.33; type C is 2.67. UAVs in type A are allocated to the closer targets to shorten their transfer time. Some selected UAVs have a low success probability due to the priority of makespan, which can explain the unsatisfied reward objective.

Solution 2 is outstanding in reward objective, indicating that the allocation plan has a high mission success rate. The average number of tasks, for type A is 2; type B is 2; type C is 2. UAV in Type-B has a higher success rate than type-C for the attack task. Therefore, all attack tasks are allocated to type B. High-value targets are completed by high-powered UAVs as much as possible to get a higher reward. However, some missions cannot be assigned to closer low-power UAVs, thus the total range of missions is increased.

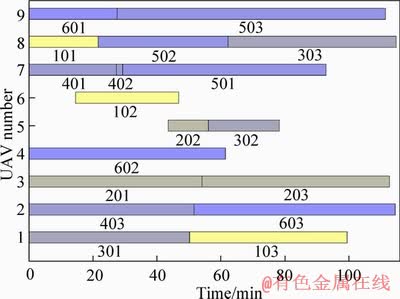
Figure 9 Gantt chart for solution 1

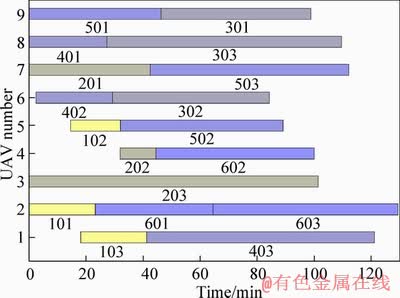
Figure 10 Gantt chart for solution 2

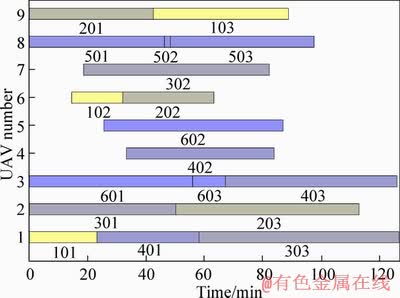
Figure 11 Gantt chart for solution 3

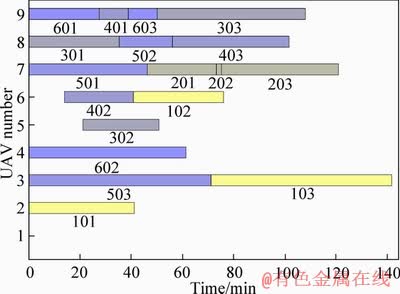
Figure 12 Gantt chart for solution 4

Solution 3 performs well in cost objective. The average number of tasks, for type A is 2.66; type B is 1.33; type C is 2. The targets with a high threat level (target 4) are allocated to types A and B to achieve the lower cost value. High-value UAVs (type C) have fewer dispatches.

The total range value of solution 4 is the lowest. In this plan, the reduction of the selected number of UAVs has reduced the range to some extent. The average number of tasks, for type A is 1; type B is 1.33; type C is 3.67. The integrated UAVs (type C) perform more tasks to avoid other UAVs visiting this target again. But the decline in the number of UAVs increases the completion time, and the increased flight time of high-value UAVs results in greater UAV cost.

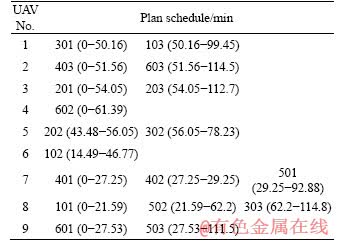
These four allocation schemes reflect the differences in the UAV and target parameter settings in the model effectively. In addition, the above Gantt chart also indicates the task schedules. Table 7 shows the timetable of solution 1(Figures in brackets indicate the start and end time of the task execution). The UAV’s last mission execution time includes the return time of the UAV.

Table 7 Mission execution flow of solution 1

Through the comparison of solutions, focusing on one optimization objective alone may degrade other objectives. The multi-objective optimization method can consider the influence of all optimization objectives better.

4.3 Validation of feasibility of optimization method

This paper proposes an improved quantum particle swarm optimization algorithm to solve this task allocation problem. In order to further verify its performance, the comparison is carried out. With unknown Pareto front, a reference solution set S^* is constructed by dominance relation in the evaluation of algorithm performance. Two performance metrics parameters are proposed to evaluate the algorithm: inversion generation distance (IGD) and hyper volume (HV) [32].

In the comparison, five algorithms are adopted: standard multi-objective particle swarm optimization (SMOPSO) [33], multi-objective particle swarm optimization based on adaptive grid (AGA-MOPSO) [29], multi-objective quantum- behaved particle swarm optimization based on crowding distance sorting (MOQPSO-CD) [34], multi-objective evolutionary algorithm based on decomposition (MOEA/D) [35] and the non- dominated sorting genetic algorithm [36]. The dominance relationships and external repository are introduced in SMOPSO as the comparison basis. Adaptive grid method is applied to handle the multi-objective problems in AGA- MOPSO. MOQPSO-CD uses the crowdeddistance to maintain the external repository. MOEA/D is based on scalarizing function. NSGA-II is well-known for its non-dominated sorting operation. The detailed parameters of these algorithms are listed in Table 8. In these parameters, w represents the weight vector; n_g represents the grid numbers of each objective; P_c and P_m represent the crossover probability and mutation probability, respectively; T denotes the neighborhood size among the weight coefficients; Z is the reference point.

These algorithms have the same size of population and repository with population of 100, external repository of 20, a maximum iteration number of 5000. All these algorithms are operated for 50 times independently, and then the mean and standard deviation of the IGD and HV are recorded for comparison.

Table 8 Basic parameter for algorithms

Figure 13 shows the inversion generation distance of each algorithm. Std denotes the standard deviation. The improved algorithm is outperformed in all algorithms with the lowest IGD value, indicating that the solutions are evenly distributed around the Pareto front. MOEA/D and NSGA-II algorithms are typical evolutionary algorithms based on cross mutation operation. Evolutionary operations are poorly stable but do not fall into a local optimum. The IMOQPSO algorithm outperforms the SMOPSO by 46.44%, by evaluating the overall performance of the particles, the retained solution distribution is more uniform with the satisfactory convergence.

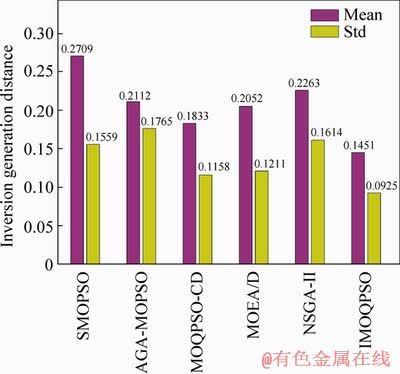
Figure 13 Inversion generation distance of algorithms

Figure 14 shows the hyper volume index of each algorithm. Different weights for particles set by the improved algorithm in different regions, especially for special boundary solutions, so that the diversity of understanding is improved with the stable convergence. IMOQPSO algorithm outperforms in all algorithms with stable performance. MOEA/D and NSGA-II algorithms have a strong ability to discover new solutions with a higher HV value. This also illustrates the effectiveness of crossover and mutation operations in population updates.

Based on the above analysis, the improved algorithm improves the ability to find high-quality solutions through the novel evaluation method, adaptive parameter control and mixed search strategy. The distribution of Pareto solutions is more uniform, and the number of optimal solutions is also stable. The improved algorithm improves the instability of the algorithm in the genetic algorithm.

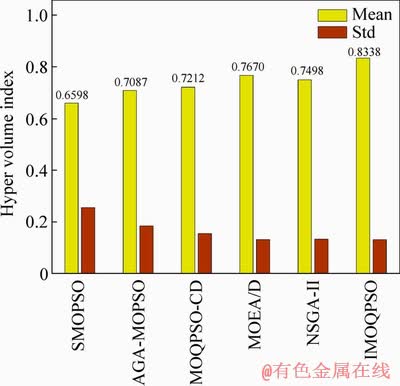
Figure 14 Hyper volume index of algorithms

5 Conclusions

In this paper, the cooperative task allocation problem for heterogeneous UAVs is considered a multi-objective and multi-constraints optimization problem. The main conclusions are drawn as follows:

Mathematical models of the heterogeneous UAVs and timing coupling tasks are established. More detailed constraints are concerned to meet the requirements for practical application in the SEAD operation. Four optimization objectives are introduced to effectively evaluate various allocation plans. The multi-layer encoding and the task scheduling method are proposed to solve the critical logical and physical constraints existing in the problem. Compared with the traditional punishment method, the proposed method can handle constraints more granularly and improve the quality of the solution.

An improved algorithm based on quantum particle swarm is constructed to solve the model effectively. To comprehensively consider the convergence and distribution of particles, a modified solution evaluation method is designed in the improved algorithm to keep reasonable reservations for some special boundary solutions. Based on the evaluation function, adaptive parameter control is designed to precisely guide each particle. The feasibility of the distribution model is proved by the simulation, and the allocation plans can effectively reflect the characteristics of the UAV and the task. The effectiveness of the improved algorithm is proved by comparison with other algorithms.

In addition, the dynamical location issue can be further studied based on the current location scheme. In the dynamic environments, some unexpected tasks may be inserted into the current schedule, and some UAVs may be added into the operation or lose capability. The algorithm should be able to handle these dynamics within a reasonable time. The number of tasks and agents participating in the replanning determines the convergence speed of the algorithm. A complete reset strategy can get a satisfactory result, but it ignores that the team has reached a conflict-free solution. The re-planning algorithm selects the number of tasks involved in the reset dynamically to balance the convergence speed and the overall reward without a full real location. A new high-value task requires large-scale resets. A limited response time situation requires a small reset.

References

[1] EUN Y, BANG H. Cooperative task assignment/path planning of multiple unmanned aerial vehicles using genetic algorithm [J]. Journal of Aircraft, 2009, 46(1): 338-343. DOI: 10.2514/1.38510.

[2] DENG Qi-bo, YU Jian-qiao, WANG Ning-fei. Cooperative task assignment of multiple heterogeneous unmanned aerial vehicles using a modified genetic algorithm with multi-type genes [J]. Chinese Journal of Aeronautics, 2013, 26(5): 1238-1250. DOI: 10.1016/j.cja.2013.07.009.

[3] ZHAI Zhao-yu, ORTEGA J M, MARTINEZ N L, RODRIGUEZMOLINA J. A mission planning approach for precision farming systems based on multi-objective optimization [J]. Sensors, 2018, 18(6): 1795. DOI: 10.3390/s18061795.

[4] CHEN Hao-xiang, NAN Ying, YANG Yi. Multi-UAV reconnaissance task assignment for heterogeneous targets based on modified symbiotic organisms search algorithm [J]. Sensors, 2019, 19(3): 734. DOI: 10.3390/s19030734.

[5] BUCKMAN N, CHOI H L, HOW J P. Partial replanning for decentralized dynamic task allocation [C]// AIAA Scitech 2019 Forum. San Diego: AIAA, 2019: 0915.

[6] EDISON E, SHIMA T. Integrated task assignment and path optimization for cooperating uninhabited aerial vehicles using genetic algorithms [J]. Computers & Operations Research, 2011, 38(1): 340-356. DOI: 10.1016/j.cor. 2010.06.001.

[7] LOZANO A, CARIDAD J, DE J P, VILLARRUBIA G G, BAJO J. Smart waste collection system with low consumption lorawan nodes and route optimization [J]. Sensors, 2018, 18(5): 1465. DOI: 10.3390/s18051465.

[8] JIANG Jun, NG K M, POH K L, TEO K M. Vehicle routing problem with a heterogeneous fleet and time windows [J]. Expert Systems with Applications, 2013, 41(8): 3748-3760. DOI: 10.1016/j.eswa.2013.11.029.

[9] SAVLA K, FRAZZOLI E, BULLO F. Traveling salesperson problems for the dubins vehicle [J]. IEEE Transactions on Automatic Control, 2008, 53(6): 1378-1391. DOI: 10.1109/ TAC.2008.925814.

[10] ZHAO Zhe, YANG Jian, NIU Yi-feng, ZHANG Yu, SHEN Lin-cheng. A hierarchical cooperative mission planning mechanism for multiple unmanned aerial vehicles [J]. Electronics, 2019, 8(4): 443. DOI: 10.3390/ electronics8040443.

[11] WANG Zhu, LIU Li, LONG Teng, WEN Yong-lu. Multi-UAV reconnaissance task allocation for heterogeneous targets using an opposition-based genetic algorithm with double- chromosome encoding [J]. Chinese Journal of Aeronautics, 2018, 31(2): 339-350. DOI: 10.1016/j.cja.2017.09.005.

[12] SCHWARZROCK J, ZACARIAS I, BAZZAN A L C, MOREIRA L H, FREITAS E P D. Solving task allocation problem in multi unmanned aerial vehicles systems using swarm intelligence [J]. Engineering Applications of Artificial Intelligence, 2018, 72: 10-20. DOI: 10.1016/j.engappai. 2018.03.008.

[13] WANG Jing-jing, ZHANG Y F, GENG L, FUH J Y H, TEO S H. A heuristic mission planning algorithm for heterogeneous tasks with heterogeneous uavs [J]. Unmanned Systems, 2015, 3(3): 205-219. DOI: 10.1142/S23013850155 00132.

[14] SHIMA T, RASMUSSEN S, SHIMA T, RASMUSSEN S. Uav cooperative decision and control: Challenges and practical approaches [M]. Society for Industrial and Applied Mathematics, 2008. DOI: 10.1137/1.97808987 18584.

[15] DE A, KUMAR S K, GUNASEKARAN A, TIWARI M K. Sustainable maritime inventory routing problem with time window constraints [J]. Engineering Applications of Artificial Intelligence, 2017, 61: 77-95. DOI: 10.1016/ j.engappai.2017.02.012.

[16] KUO R J, CHENG W C. Hybrid meta-heuristic algorithm for job shop scheduling with due date time window and release time [J]. International Journal of Advanced Manufacturing Technology, 2013, 67(1-4): 59-71. DOI: 10.1007/s00170- 013-4753-z.

[17] SCHUMACHER C, CHANDLER P, PACHTER M, PACHTER L. Uav task assignment with timing constraints via mixed-integer linear programming [C]// AIAA 3rd Unmanned Unlimited Technical Conference. 2004: 6410. DOI: 10.2514/6.2004-6410.

[18] SCHUMACHER C, CHANDLER P R, PACHTER M, PACHTER L S. Optimization of air vehicles operations using mixed-integer linear programming [J]. Journal of the Operational Research Society, 2007, 58(4): 516-527. DOI: 10.1057/palgrave.jors.2602176.

[19] SINGH M R, MAHAPATRA S S. A quantum behaved particle swarm optimization for flexible job shop scheduling [M]. Pergamon Press, 2016. DOI: 10.1016/j.cie.2015.12.004.

[20] BUI K H, JUNG J, CAMACHO D. Consensual negotiation- based decision making for connected appliances in smart home management systems [J]. Sensors, 2018, 18(7): 2206. DOI: 10.3390/s18072206.

[21] PEREZ-CARABAZA S, BESADA-PORTAS E, LOPEZ- OROZCO J A, JESUS M. Ant colony optimization for multi- uav minimum time search in uncertain domains [J]. Applied Soft Computing, 2018, 62: 789-806. DOI: 10.1016/j.asoc. 2017.09.009.

[22] MILORADOVIC B, CURUKLU B, EKSTROM M. A genetic planner for mission planning of cooperative agents in an underwater environment [C]// IEEE Symposium Series on Computational Intelligence. Athens: IEEE, 2016: 1-8. DOI: 10.1109/SSCI. 2016.7850163.

[23] SUN Jun, FENG Bin, XU Wen-bo. Particle swarm optimization with particles having quantum behavior [C]// Congress on Evolutionary Computation. Portland: IEEE, 2004: 325-331. DOI: 10.1109/CEC.2004.1330875.

[24] CHANDLER P, SPARKS A. Decentralized control for an autonomous team [C]// AIAA Unmanned Unlimited Conference 2013. San Diego: AIAA, 2013. DOI: 10.2514/6.2003-6571.

[25] CHEN Qing-yang, LU Ya-fei, JIA Gao-wei, LI Yue, ZHU Bing-jie, LIN Jun-can. Path planning for uavs formation reconfiguration based on dubins trajectory [J]. Journal of Central South University, 2018, 25: 2664-2676. DOI: 10.1007/s11771-018-3944-z.

[26] LIN Qiu-zhen, LIU Song-bai, ZHU Qing-ling, TANG Chao-yu, SONG Rui-zhen, COELLO C A C, WONG K C, ZHANG Jun. Particle swarm optimization with a balanceable fitness estimation for many-objective optimization problems [J]. IEEE Transactions on Evolutionary Computation, 2016, 22(1): 32-46. DOI: 10.1109/TEVC.2016.2631279.

[27] WANG Rui, PURSHOUSE R C, FLEMING P J. Preference- inspired coevolutionary algorithms for many-objective optimization [J]. IEEE Transactions on Evolutionary Computation, 2013, 17(4): 474-494. DOI: 10.1109/TEVC. 2012.2204264.

[28] LI Mi-qing, YANG Sheng-xiang, LIU Xiao-hui. Shift-based density estimation for pareto-based algorithms in many-objective optimization [J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 348-365. DOI: 10.1109/TEVC.2013.2262178.

[29] YANG Jun-jie, ZHOU Jian-zhong, FANG Reng-cun, LI Ying-hai, LIU Li. Multi-objective particle swarm optimization based on adaptive grid algorithms [J]. Journal of System Simulation, 2008, 20(21): 5843-5847. DOI: 10.1088/0953-8984/20/42/425208.

[30] AL M N, PETROVSKI A, MCCALL J. D2MOPSO: Mopso based on decomposition and dominance with archiving using crowding distance in objective and solution spaces [J]. Evolutionary Computation, 2014, 22(1): 47-77. DOI: 10.1162/EVCO_a_00104.

[31] XU Ming-ming, ZHANG Liang-pei, DU Bo, ZHANG Le-fei, FAN Yan-guo, SONG Dong-mei. A mutation operator accelerated quantum-behaved particle swarm optimization algorithm for hyperspectral endmember extraction [J]. Remote Sensing, 2017, 9(3): 197. DOI: 10.3390/rs9030197.

[32] FAN Zhun, LI Wen-ji, CAI Xin-ye, WEI Cai-min, ZHANG Qing-fu, DEB K, GOODMAN E D. Push and pull search for solving constrained multi-objective optimization problems [J]. Swarm and Evolutionary Computation, 2017, 44: 665- 679. DOI: 10.1016/j.swevo.2018.08.017.

[33] COELLO C A C, LECHUGA M S. MOPSO: A proposal for multiple objective particle swarm optimization [C]// Congress on Evolutionary Computation. 2002: 1051-1056. DOI: 10.1109/CEC.2002.1004388.

[34] PENG Guang, FANG Yang-wang, PENG Wei-shi, CHAI Dong, XU Yang. Multi-objective particle optimization algorithm based on sharing–learning and dynamic crowding distance [J]. Optik, 2016, 127(12): 5013-5020. DOI: 10.1016/j.ijleo.2016.02.045.

[35] ZHANG Qing-fu, LI Hui. MOEA/D: A multiobjective evolutionary algorithm based on decomposition [J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI: 10.1109/TEVC.2007.892759.

[36] DEB K, PRATAP A, AGARWAL S, MEYARIVAN T. A fast and elitist multiobjective genetic algorithm: NSGA-II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI: 10.1109/4235.996017.

(Edited by ZHENG Yu-tong)

中文导读

基于多目标优化算法的异构多无人机协同任务分配

摘要：近年来，关于多无人机在复杂任务中的应用有了广泛的探索。无人机具有部署灵活、成本低廉和自持力强的优点，合理的协同方案可以实现无人机之间的高效信息融合与资源互补，突破单架无人机能力限制，提升任务执行效率。在现实应用中，异构任务分配需要满足多种现实约束，如飞行平台差异、任务时间窗、任务耦合关系等。因此，作为无人机集群应用的顶层规划，异构无人机任务分配可以建模为基于无人机动力学约束的多目标优化问题。在问题模型构建中，设计了多层编码策略和约束调度方法来处理多种耦合约束，引入了任务时间、任务收益、无人机损耗和飞行航程四个优化目标对分配方案进行综合评估。为高效求解这一高维多目标优化问题，本文提出了一种改进的多目标量子粒子群算法，即利用改进的非支配解评估方法来引导算法进化，综合考虑解的收敛性和分布性，并保留了合理的边界解。仿真结果验证了构建模型的可行性与改进算法的有效性。

关键词：无人机；协同任务分配；异构；模型约束；多目标优化；解评估方法

Foundation item: Project(61801495) supported by the National Natural Science Foundation of China

Received date: 2019-04-17; Accepted date: 2019-10-08

Corresponding author: JIA Gao-wei, PhD, Lecturer; Tel: +86-731-87007138; E-mail: ji_as@126.com; ORCID: 0000-0001-5786-6436