J. Cent. South Univ. Technol. (2008) 15(s1): 013-016

DOI: 10.1007/s11771-008-304-4

Viscoelastoplastic constitutive model for creep deformation behavior of asphalt sand

YE Yong(叶 永)^{1, 2}, YANG Xin-hua(杨新华)¹, CHEN Chuan-yao(陈传尧)¹

(1. College of Civil Engineering and Mechanics, Huazhong University of Science and Technology,

Wuhan 430074, China;

2. College of Civil and Hydroelectric Engineering, Three Gorges University, Yichang 443002, China)

Abstract: A uniaxial viscoelastoplastic model that can describe whole creep behaviors of asphalt sand at different temperatures was presented. The model was composed of three submodels in series, which describe elastoplastic, viscoelastic and viscoplastic characteristics respectively. The constitutive equation was established for uniaxial loading condition, and the creep representation was also obtained. The constitutive parameters were determined by uniaxial compression tests under controlled-stress of 0.1 MPa with five different test temperatures of 20, 40, 45, 50 and 60 ℃. Expressions of the model parameters in terms of temperatures were also given. The model gave prediction at various temperatures consistent with the experimental results, and can reflect the total deformation characterization of asphalt sands.

Key words: asphalt sand; viscoelastoplastic model; creep experiment; model parameters

1 Introduction

Asphalt mixture exhibits linear viscoelasticity at small strain^[1]. However, at larger strain or higher temperature, its behavior is non-linear, and cannot be adequately modeled by a linear viscoelastic approximation^[2]. Non-linear viscous behaviors of asphalt mixture have been investigated by many researchers^[3-4]. Their work shows that the responses of asphalt mixture to loads are very complex. As an approximation, mechanical properties of asphalt mixture were considered separately according to whether deformations measured in creep and recovery tests are time dependent and recoverable or not during unloading^[5-6]. KETTIL  et al^[7] proposed an elasto-visco-plastic model for asphalt concrete to predict inelastic deformation in road structures. In his model, elastic strain was given by the isotropic Hooke's law, viscoplastic strain was defined by the flow potential and viscoplastic parameter, and the strain hardening power law was used to describe evolution of viscoplastic strain. GONZ?LEZ et al^[8] developed a viscoplastic model in which elastic and viscoplastic strains were evaluated individually and the Young’s modulus and the viscosity parameter were strain-rate dependent. CHEN et al^[9] investigated mechanical behavior of brittle rock based upon the above approaches. However, because elastoplastic or viscoelastic strain occurring during creep tests of asphalt sand is not concerned in the above models, it is difficult to apply them to simulate the real deformation behavior perfectly. The objective of this paper is to establish a viscoelastoplastic (VEP) model with elastoplastic (EP), viscoelastic (VE) and viscoplastic (VP) strain components for asphalt sand experimentally.

The basic strategy for the constitutive model of asphalt mixture is to develop separate models for the different strain components and then to integrate them to a whole model. Elastic and plastic responses are combined as an EP model, and viscoelastic and viscoplastic responses are characterized by VE and VP models, respectively. Thus, the total strain can be expressed as

                            (1)

where ε_ep, ε_ve and ε_vp denote EP, VE and VP strains respectively. The material model at uniaxial compression is shown in Fig.1.

The EP part is described by a submodel combining two springs and a frictional element. Its constitutive equation can be written as

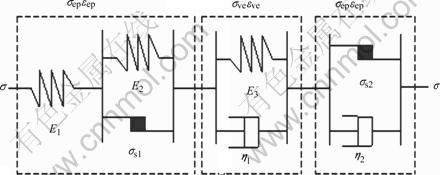
Fig.1 Constitutive scheme for viscoelastoplastic model

       (2)

where E₁ and E₂  are Young’s moduli of the springs, and σ_s1 is yield stress of the frictional element.

For the VE part, the constitutive equation is

                          (3)

where E₃ is Young’s modulus of the third spring, and η₁ is viscosity coefficient of the first dashpot.

The axial VP strain for uniaxial constant stress loading is assumed to follow a strain hardening model of the following form:

                                 (4)

where ε_vp is the VP strain, g(σ) is the uniaxial stress loading function, and A and m are material constants. The stress loading function is given as

       (5)

where the angle bracket denotes a on/off operator.

Accordingly, the strain hardening model can be described as follows:

          (6)

where C, m and n are material constants, and can be determined experimentally.

The constitutive equation of the integrated model can be obtained. Under uniaxial compression σ=σ₀H(t), the total strain response of the VEP model is

              (7)

The experimental Bitumen is AH-70, whose softening point is 47 ℃. The aggregate sizes are from 1.18 mm to 2.36 mm. Cylindrical asphalt sand specimens are with dimension of Φ50 mm×50 mm and aggregate volume fraction of 64%. Under constant stress loading of 0.1 MPa, tests are performed at five different tempera- tures of 20, 40, 45, 50 and 60 ℃.

First, two yield stresses σ_s1 and σ_s2 need to be defined. GONZ?LEZ et al^[8] concluded from the experiments that the yield stress of asphalt mixture is 0.04 MPa≤σ_s≤0.06 MPa. The plastic property of asphalt mixture mainly comes from bitumen, so it is reasonable that the yield stress of asphalt sand is approximately regarded as that of asphalt mixture, and it can be assumed that σ_s1 is equal to σ_s2. Accordingly, σ_s1 and σ_s2 is postulated as 0.05 MPa in this paper. After that, there are still seven quantities to be determined: E₁, E₂, E₃, η₁, C, m and n. These constitutive parameters can be determined by fitting Eqn.(7) with the experimental data through the least square technique. A nonlinear fitting procedure is developed based on creep tests. The obtained parameters are provided in Table 1. It is found from Table 1 that these quantities are all dependent upon testing temperature conditions. The correlation coefficients greater than 0.99 show a high precision fit.

In succession, the model parameters are regarded as functions of testing temperature T, and the linear or second-order polynomial expressions of parameter functions are given as

E₁(T)=0.001 3T²-0.150 6T+6.049 4                (8)

E₂(T)=0.175 7T²-4.010 2T+20.504 8               (9)

E₃(T)=0.007 9T²-0.937 7T+29.120 1              (10)

η₁(T)=-122.210 1T+9 858.7                      (11)

C(T)=0.278 8T+10.814 1                        (12)

Table 1 Model parameter values at σ=0.1 MPa and different test temperatures

m(T)=0.014 2T+1.077 2                          (13)

n(T)= 0.004 4T-0.659 5                          (14)

To verify the validity of the VEP material model, Eqn.(7) combined with Eqns.(8)-(14) are used to simulate the deformation behavior of asphalt sand at different temperatures. For the sake of convenience for comparison, simulating and experimental results are both plotted in Fig.2. The dashed lines denote the results from the model, and the solid lines show the experimental results. As is apparent from visual inspection, the model has remarkably good accuracy and can capture most of the main features from the experimental curves except for a small discrepancy in the deceleration creep stage at 20 ℃. In particular, the model can predict the acceleration creep behavior of asphalt sand rather well from the lower temperature (20 ℃) to the higher tem- perature (60 ℃).

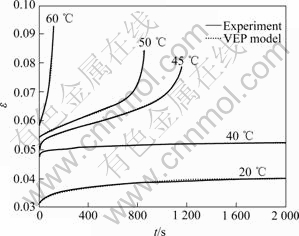
Fig.2 Comparison between predictions and experiments at σ=0.1 MPa and different temperatures

Fig.3 shows variation of VP strain, expressed as a percent of total strain, with loading time for all five temperatures. It can be seen that the composition percent of VP strain increases with the increase of testing temperature and time. When temperature approaches the softening point 47 ℃ of Bitumen AH-70, the VP strain increases rapidly. At the third stage of creep, the maximum VP strain from the proposed model could account for about 2% in total strain at 20 ℃, and its percent even exceeds 20% at 60 ℃, approximately decuple at 20 ℃.

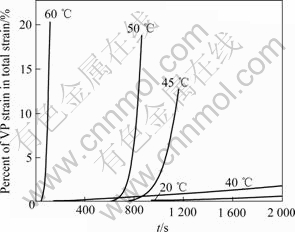
Fig.3 VP strain percent at σ=0.1 MPa and different temperatures

1) The VEP model is proposed for simulating creep behavior of asphalt sand by combining three submodels, which describe EP, VE and VP strains respectively. It can cover all of elastoplastic, viscoelastic and viscoplastic deformation components in a creep process.

2) Uniaxial compressive creep tests are carried out at five temperatures. The experimental data are used to determine material parameters, and expressions of parameter functions with temperatures are also obtained.

3) By comparison, the VEP model shows a good match to the experimental data at different temperatures.

4) Due to the softening point 47 ℃ of Bitumen AH-70, the VP strain rapidly increases as temperature rises from 40 ℃ to 60 ℃. In particular, its percent in total strain even exceeds 20% at 60 ℃, so that linear viscoelastic models fail to describe deformation of asphalt sand.

[1] KIM Y R, LITTLE D N. Linear viscoelastic analysis of asphalt mastics [J]. Journal of Materials in Civil Engineering, 2004, 16(2): 122-132.

[2] DESHPANDE V S, CEBON D. Uniaxial experiments on idealized asphalt mixtures [J]. Journal of Materials in Civil Engineering, 2000, 12(3): 262-271.

[3] DESHPANDE V S, CEBON D. Steady-state constitutive relationship for idealized asphalt mixtures [J]. Mechanics of Materials, 1999, 31: 271-287.

[4] BANDYOPADHYAYA R, DAS A, BASU S. Numerical simulation of mechanical behaviour of asphalt mix [J]. Construction and Building Materials, 2007, 18: 1-8.

[5] ZHAO Y Q. Permanent deformation characterization of asphalt concrete using a viscoelastoplastic model [D]. North Carolina: Department of Civil Engineering, North Carolina State University, 2002.

[6] BAHUGUNA S. Permanent deformation and rate effects in asphalt concrete: Creep modeling and numerical implementation [D]. Cleveland: Department of Civil Engineering, Case Western Reserve University, 2003.

[7] KETTIL P, LENHOF B, RUNESSON K, WIBERG N E. Simulation of inelastic deformation in road structures due to cyclic mechanical and thermal loads [J]. Computers & Structures, 2006, 85: 59-70.

[8] GONZ?LEZ J M, MIQUEL CANET J, OLLER S, MIRO R. A viscoplastic creep model with strain rate variables for asphalt mixtures-numerical simulation [J]. Computational Materials Science, 2007, 38: 543-560.

[9] CHEN Feng, SUN Zong-qi, XU Ji-cheng, ZHANG Jing-yi. A composite material model for investigation of microfracture mechanism of brittle rock subjected to uniaxial compression [J]. J Cent South Univ Technol, 2001, 8(4): 258-262.

(Edited by YANG You-ping)

Foundation item: Project(10672063) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: YANG Xin-hua, Doctor; Tel: +86-27-87540153; E-mail: yangxinh@263.net