J. Cent. South Univ. Technol. (2007)03-0374-06
DOI: 10.1007/s11771-007-0074-4
Thermal contact conductance at continuous roll-casting interface
HU Shi-cheng(胡仕成), MA Wei-ce(马维策), DU Lei(杜 磊), LI Xiao-qian(李晓谦), ZHONG Jue(钟 掘)
(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: The effects of surface roughness, strain rate, friction coefficient and pressure on real contact area were analyzed based on the research of Stupkiewicz. The real contact area model taking account of the effect of friction and deformation of material was obtained. The model of contact conductance at the rolling interface was obtained by integrating the specific feature of heat transfer through the interface of continuous roll-casting. The results indicate that the real contact area increases obviously when the material is under yield, and the real contact area varies inversely with surface roughness, whereas it varies exponentially with friction coefficient, strain rate and pressure, and the power factor depends on strain rate.
Key words: real contact area; strain rate; pressure; thermal contact conductance
1 Introduction
The heat is produced during the melt aluminum solidification and crystallization at the zone between two reversely rotating rollers and transfers to the cooling water through the work interface and roller in the process of continuous roll casting. In this process, heat transfer at the interface is very important, and it directly affects the process of nuclei, solidification,growth and rheological forming. When liquid metal first approaches the roller surface, bring about contact at the peaks of asperities, rapid cooling at these peaks causes solidification, nucleate, shrinkage, growth and then a fine stable crust of solidified of metal is formed. The solidified metal brings about plastic rheologic. The heat transfer coefficient at the interface is a function of temperature, coating film and oxide films and pressure. Recently, the fluid flowing, temperature fields and distribution of rolling force in the process of roll-casting are lively researched, and some simulating mathematical models are proposed[1-8]. The theory of roll-casting is developed, but the basic researches with regard to material property at the mushy zone and the heat transfer coefficient at the interface are still lack.
The metal under rolling conditions brings about elastic, elastic-plastic and plastic deformation in the process of roll-casting. The heat is mainly transferred by conduction in the real contact area when the radiation, conduction of media at the interface and convection are ignored, and the thermal contact conduction is decided by the following factors, such as the real contact area, the thickness of surface layers (oxide films, alloy layers and lubrication layer) and the temperature. The recent researches about the thermal contact resistance are mainly under the condition of the static interface without sliding[9], elastic deformation and small strain plastic deformation. The rolling interface possesses the following characteristics: 1) high temperature; 2) larger deformation, the plastic deformation of materials happens under rolling pressure; 3) there exists fore- sliding and afterwards sliding; 4) the metal atoms diffuse to the surface of rollers under high temperature and large pressure, so the materials are transferred to the rollers. At the same time, the oxide layer is partly removed by rubbing, which gives rise to the contacted material proning to sticking. Due to the complexity of the forming interface, it will lead to errors to analyze the temperature field of roll-casting process by directly citing the existing thermal contact conduction models.
In this paper, the effects of roughness, bulk strain rate, friction coefficient and pressure on real contact area were analyzed based on the researches of Stupkiewicz. The aim is to obtain the thermal contact conductance model in the process of roll-casting through analyzing the deformation of asperities.
2 Model of real contact area at roll interface
2.1 Deformation analyzing
The asperities of aluminum surface bring about plastic deformation under the rolling pressure, which leads to the real contact area between the surface of aluminum and rollers to increase in the process of roll-casting. Based on the researches of STUPKIEWICZ et al[10], the surface asperities of the workpiece together with a thin layer of inhomogeneous plastic deformation around the asperities can be replaced by a homogeneous surface layer (Fig.1), thus we can only consider macroscopic (averaged) stresses and strains in the layer, and the stresses and strains at the whole layer can be considered as constant because the thickness of surface layer is much less than that of workpiece.
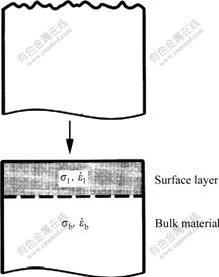
Fig.1 Thin homogeneous surface layer representing region of inhomogeneous deformation field of asperities
We assume a linear relation between the contact area and volumetric strain in the layer[10], namely
 (1)
(1)
where a is the real contact area,a=Ar/An; ev,l, ev, max are the bulk strain of surface layer and the maximum bulk strain corresponding to a=1, respectively, namely
 (2)
(2)
where  is the bulk strain rate of surface layer.
is the bulk strain rate of surface layer.
So the maximum logarithmic volumetric strain of two-dimensional wedge-like asperities is[10]
 (3)
(3)
We use the following expression (the linear term of Taylor expansion of Eqn.(3) at q=0):
 (4)
(4)
where h=H0/l0,H0 is the thickness of surface layer; l0 is the half width of wedge-like asperity; q is the initial inclination angle; the parameter n depends on the initial surface roughness and is defined as the fraction of volume occupied by the (undeformed) asperities in a layer contained between the highest asperity peaks and the deepest asperity valleys before deformation. For wedge-like asperities, v=1/2.
Assuming the bulk body is rigid plasticity, according to the yield condition and flow rule, STUPKIEWICZ et al[10] obtained the yield condition of asperities under the condition that bulk material brought plastic deformation:
 (5)
(5)
where Pt and Pn are the dimensionless shear stress and normal stress, respectively, 
 , sy is yield stress,MPa; pn and tt are the normal stress and effective friction stress,MPa; Ev is the dimensionless effective bulk strain rate,
, sy is yield stress,MPa; pn and tt are the normal stress and effective friction stress,MPa; Ev is the dimensionless effective bulk strain rate, ,
,  is the average strain rate; g1, g2 and g3 are functions concerned with area contact fraction.
is the average strain rate; g1, g2 and g3 are functions concerned with area contact fraction.
We can obtain the relation between real contact area and pressure by considering the effect of friction, asperity configuration, material property and deformation rate.
 (6)
(6)
where vf is the flattening velocity; l is half of the asperity spacing.
2.2 Analysis of factors affecting on real contact area
The formula of real contact area a concerned with yield strength, thickness of surface layer, surface rough, friction coefficient, bulk strain rate and pressure is obtained through the above analysis. The computation model of real contact area was obtained through computing the effect of surface rough, strain rate, pressure and pressure on real contact area at certain layer thickness because we cannot directly obtain the relation between real contact area and pressure.
2.2.1 Thickness of surface layer
For wedge-like asperities, we take roughness to be σa=1 mm,Pt=0,the results of real contact area varying with pressure for h is 0.5, 1.0 and 1.5, respectively (Fig.2). It can be seen that the effect of parameter h on real contact area is obvious when dimensionless pressure is 0.05n<4.00. SUTCLIFFE[11] found that parameter h is 0.48 and 0.46 corresponding to bulk strain of 0.36 and 0.38, respectively, according to the bulk strain results of experiment and theory.
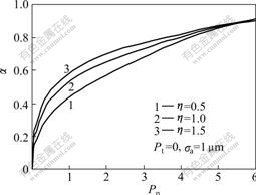
Fig.2 Real contact area as function of pressure at different layer thicknesses
2.2.2 Roughness
Surface roughness is an important parameter affecting real contact area, and the real contact area decreases with roughness increasing. When the roughness of surface is smaller, more obvious asperities are prone to deforming under pressure (Fig.3). The effect of roughness on real contact area becomes small with increasing pressure.
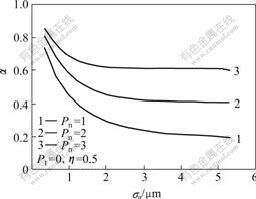
Fig.3 Real contact area as function of roughness
2.2.3 Friction coefficient
Friction produces shear stress, and real contact area increases because of friction (Fig.4). It can be seen that the effect of friction on real contact area is not obvious, and real contact area increases by 20% because of friction when the friction coefficient is 0.9. PHILLP et al[12] pointed out that the friction coefficient at the roll-casting interface depends on solid phase fraction of solidified metal, it is about 0.2 when the solid phase fraction is 30%-70%, whereas it reaches 0.5 when solid phase fraction is bigger than 70%. From Fig.4, it can be seen that real contact area increases by 5% when friction coefficient is 0.5.
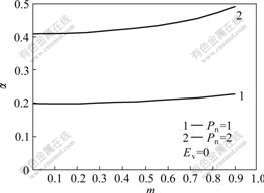
Fig.4 Real contact area as function of friction coefficient under different pressures
2.2.4 Bulk strain rate
Real contact area will increase with increasing bulk strain rate(Fig.5). The results of experiment and theory indicate that the real contact area increases when the plastic deformation of bulk material takes place because the asperities are prone to deform under this condition. The bulk strain rate is about 0.15 s-1 in the process of general roll-casting, and it reaches 3 s-1 in the process of high speed roll-casting, so it will bring about great error to calculate the real contact area if ignoring the effect of bulk plastic deformation.
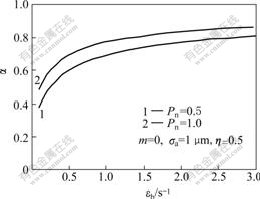
Fig.5 Real contact area as function of bulk strain rate under different pressures
2.2.5 Pressure
Pressure is one of the most important parameters to affect real contact area. The real contact area fraction is only 0.01%-0.10% without pressure. Real contact area will increase obviously by increasing of the pressure to flat the asperities. The real contact area in the process of roll-casting is obviously bigger than that without bulk deformation, because pressure introduces material yielding and produces bulk deformation. From Fig.6 it can be seen that real contact area increases by exponential with pressure when bulk deformation is considered. The curve shape of real contact area as a function of pressure is different corresponding to different bulk strain rates. This indicates that the exponential is different and varies with bulk strain rate under the condition of bulk deformation.
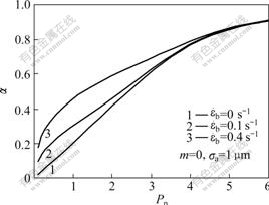
Fig.6 Real contact area as function of pressure
2.3 Model of real contact area at roll interface
The model of real contact area as a function of surface roughness, friction coefficient, bulk strain rate and pressure is obtained based on the above analysis.
 (7)
(7)
From Figs.2-6, it can be seen that the real contact area varies inversely with surface roughness, exponentially with bulk strain rate and pressure, and the exponential is a function of bulk strain rate.
Adopt the dimensionless parameters convenient for describing and computing, and define  =1 mm,
=1 mm,  0= 1 s-1),the dimensionless roughness and strain rate are
0= 1 s-1),the dimensionless roughness and strain rate are ,
, , respectively.
, respectively.
So the real contact area model can be expressed as
 (8)
(8)
Real contact area is a function of friction coefficient, the relation can be obtained according to the Misses plasticity conditions.
 (9)
(9)
The friction stress of tf equals 0 under reasonable unidirectional compress condition without friction.
when sn=ssf, K=ssf, so
 (10)
(10)
Assuming the real contact area is  when there exists relative sliding, the following relation can be obtained
when there exists relative sliding, the following relation can be obtained
 (11)
(11)
 (12)
(12)
Uder the condition of non-relative sliding, it can be gotten
 (13)
(13)
The following relation can be obtained by comparing the above two formulas:
 (14)
(14)
 (15)
(15)
where α0 is corresponding to m=0.
So the regression model of real contact area is

 (16)
(16)
In the process of general roll-casting, surface roughness is 1 mm, bulk strain rate is 0.15 s-1, friction coefficient is 0.5, so the following relation between real contact area and pressure can be obtained through regressing the results computed with formula (6):
 (17)
(17)
The maximum error of the model results is 0.006; the average error is 0.003 8, and the average relative error is 2.2%.
In the process of high speed roll-casting, the bulk strain rate reaches above 1 s-1, the regression model of real contact area is as follows by adopting the bulk strain rate to be 1.5 s-1:
 (18)
(18)
The maximum error of the model results is 0.01, average error is 0.004 7, the average relative error is 1.43%.
3 Thermal contact conductance at roll
interface
In the process of roll-casting, the temperature of roller surface reaches above 200 ℃ when the metal leaves the roll zone, the minimum temperature on the roll surface is also above 50 ℃ owing to the strong cooling by the roller inner water, and the temperature of roll surface in the process of high speed roll-casting is even higher, and at the same time, the roller shell is under the moist environment and prone to forming oxide film. The oxide layer is very thin under the room temperature, for example, the thickness of oxide film for iron and copper is about 1 to 3 nm. And the thickness of oxide film will increase obviously at high temperature. The thickness of oxide film for high chrome cast iron roller is about 50 mm. The thickness of oxide film for roller material at room temperature is about 1 mm, and it reaches several tens of micronmeter above 200 ℃. The tunneling effect of electron is ultimately vanished at the real contact zone when the thickness of oxide film reaches the level of micronmeter. The boundary resistance caused by acoustic mismatch is much smaller than the conduction resistance of oxide film. Therefore, we can consider that thermal contact resistance is mainly caused by gap gas, oxide film and lubrication media at the roll-casting interface. The conductivity of air is 0.026 24 W/(m?K) at the room temperature, and it reaches 0.046 59 W/(m?K) at 600 K. The real contact area fraction is only 0.1% without pressure, the gap gas has some effect on interface heat transfer under this condition. In the process of roll-casting, the bulk strain rate reaches 0.15 s-1 because the material undergoes plastic deformation under the roll pressure. The real contact area fraction can reach 40% when the pressure is bigger than the yield stress following the above analysis. But in the process of high speed roll-casting, the real contact area fraction can even exceed 70% because the bulk strain rate is increased. So we can ignore the effect of gap gas on thermal contact conductance at the roll interface. The conductivity of graphite by way of lubrication media is about 59 W/(m?K), and it is bigger than that of oxide film of roller shell. The thermal contact resistance will decrease because the conductivity of graphite is bigger than that of gas when the gap is filled with graphite.
Assuming that the thicknesses of oxide film of roller and work material are lox1, lox2, and the conductivities are kox1, kox2, respectively. The thickness of lubrication media is llub, and conductivity is klub.
So the thermal contact conductance in the process of general roll-casting can be expressed as

(19)
The thermal contact conductance in the process of high speed roll-casting can be expressed as
 (20)
(20)
4 Conclusions
1) The real contact area increases when the bulk material is under yielding, and it varies inversely with roughness, exponentially with friction coefficient, bulk strain rate and pressure, the real contact area model taking into account of friction and bulk deformation can be expressed as
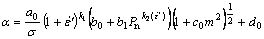
2) The exponent varies with bulk strain rate in the relation of real contact area and pressure, the bulk strain rates of general and high speed roll-casting are different. The regression models of real contact area are as follows:
General roll-casting: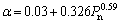
High speed roll-casting:
3) The heat is mainly transferred through real contact area at the roll-casting interface, the main factors affecting the interface of heat transfer are the thickness of oxide film and the thickness of lubrication and its conductivity. Thermal contact conductance can be expressed as
General roll-casting:

High speed roll-casting:

References
[1] CHANG J C, WENG CⅠ. Numerical modeling of twin-roll casting by the coupled fluid flow and heat transfer model[J]. International Journal for Numerical Methods in Engineering, 1997, 40(3): 493-509.
[2] BRADBURY P J, HUNT J D, Coupled fluid flow, deformation and heat transfer model for a twin roll caster[J]. Minerals, Metals & Materials Soc, 1995, 125(2): 739-746.
[3] SEYEDEIN S H, HASAN M. Numerical simulation of turbulent flow and heat transfer in the wedge-shaped liquid metal pool of a twin-roll caster[J]. Numerical Heat Transfer, Part A: Application. 1997, 31(2): 393-410.
[4] JARRY P, TOITOT D, MENET P Y. Thermo-mechanical modeling of 3C roll casting of alloys[J]. Metals & Materials Soc, 1996, 47(4): 905-911.
[5] YUN M, HUNT J D, EDMONDS D V. Heat line formation during roll-casting of aluminum alloys at thin gauges[J]. Journal de Physique, 1993, 3(7): 227-230.
[6] YUN M, LOKYER S, HUNT J D. Twin roll casting of aluminum alloys[J]. Material Science and Engineering A, 2000, A280(1): 116-123.
[7] WANG B, ZHANG J, ZHANG Y, et al. Numerical and physical simulation of a twin-roll strip caster[J]. Journal of University of Science and Technology Beijing , 2006, 13(5): 393-400. (in Chinese)
[8] SANTOS C A, SPIM J A, GARCIA A. Modeling of solidification in twin-roll strip casting[J]. Journal of Materials Processing Technology, 2000, 102(1/3): 33-39.
[9] COOPER M G, MIKIC B B, YOVANOVICH M M. Thermal contact conductance[J]. Int J Heat Mass Transfer, 1969, 23(12): 279-300.
[10] STUPKIEWICZ S, MORZ Z. Phenomenological model of real contact area evolution with account for bulk plastic deformation in metal forming[J]. International Journal of Plasticity, 2003, 19(2): 323-344.
[11] SUTCLIFFE M P F. Surface asperity deformation in metal forming process[J]. Int J Mech Sci, 1988, 30(11): 847-868.
[12] PHILLP J, DENIS T, PIERRE Y M, Thermo-mechanical modeling of 3C roll casting of alloys[J]. Light Metals, 1996, 15(4): 905-911.
Foundation item: Project(1999064906) supported by the National Key Fundamental Research and Development of China
Received date: 2006-06-28; Accepted date: 2006-09-25
Corresponding author: HU Shi-cheng, PhD; Tel: +86-731-8876167; E-mail: schenghu@163.com(Edited by LI Xiang-qun)