DOI: 10.11817/j.ysxb.1004.0609.2021-40002

扭转角和晶向对含微缺陷纳米镍双晶断裂的影响

丁  军¹，童  权¹，张圣来¹，王路生²，黄  霞¹，宋  鹍¹，路世青¹

(1. 重庆理工大学 机械工程学院，重庆 400054；

2. 合肥工业大学 材料科学与工程学院，合肥 230009)

摘  要：采用分子动力学方法研究了单轴拉伸载荷下扭转晶界(Twist boundary, TB)扭转角和晶向对含微缺陷的纳米镍双晶断裂的影响机理。结果表明：扭转角和晶向决定了扭转晶界处失配位错密度大小，影响位错的形核与发射。随着扭转角的增加，晶界处位错形核与发射增多，裂纹扩展加快，孔洞变形变小，镍双晶断裂从0°时由孔洞导致变为45°时由裂纹扩展导致。对含有不同晶向扭转晶界的镍双晶，(110)扭转晶界镍双晶相比于(010)和(111)扭转晶界镍双晶具有更大的裂纹扩展速率，塑形变形的集中也让孔洞长大不明显，并在应变达到0.3之前就已经完全断裂。而(110)与(111)扭转晶界镍双晶裂纹扩展较难，孔洞长大明显，并在应变达到0.3时也未发生完全断裂，因此拥有更好的延展性。

关键词：镍双晶；分子动力学；扭转晶界；扭转角；晶向；孔洞；裂纹

文章编号：1004-0609(2021)-08-2146-14　　     中图分类号：TG111.91 　     文献标志码：A

引文格式：丁  军, 童  权, 张圣来, 等. 扭转角和晶向对含微缺陷纳米镍双晶断裂的影响[J]. 中国有色金属学报, 2021, 31(8): 2146-2159. DOI: 10.11817/j.ysxb.1004.0609.2021-40002

DING Jun, TONG Quan, ZHANG Sheng-lai, et al. Influence of twist angle and orientation on fracture of nano-nickel bicrystal with micro-defects[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(8): 2146-2159. DOI: 10.11817/j.ysxb.1004.0609.2021-40002

镍基合金具有良好的高温强度、抗氧化性及抗腐蚀性能，广泛用于航空发动机和燃气轮机的涡轮叶片热端部件^[1-2]。由于服役过程中复杂载荷的耦合作用，会导致镍基合金材料产生裂纹等缺陷而引起零部件断裂失效^[3-4]，因此研究含有微观缺陷的镍基高温合金断裂问题以及不同条件下的裂纹扩展性能对航空发动机以及涡轮叶片等热端部件的研发和生产具有一定的指导意义。同时，为进一步探明微裂纹和孔洞对镍基合金材料失效破坏微观机理，有必要从微观尺度开展镍基合金材料裂纹萌生、贯穿和扩展以及微孔洞演化形成机理及其影响因素研究。

到目前为止，已有许多学者对镍基合金材料内微裂纹扩展和孔洞演化进行了相关研究。CATON等^[5]通过实验研究了650 ℃下IN100镍基合金材料疲劳裂纹的宏观扩展行为，结果表明疲劳寿命差异源于裂纹的产生阶段和早期裂纹(裂纹尺寸小于100 μm)的扩展阶段。KEVINSANNY等^[6]通过实验研究了镍基高温合金不同微缺陷拉压疲劳性能，研究发现疲劳强度在不同的晶粒尺寸下对缺陷的敏感性不同，当晶粒尺寸越小时，镍基合金更容易受到微缺陷的影响。张宝宁等^[7]研究了GH4742合金的疲劳裂纹扩展行为，发现裂纹的扩展方式受相邻晶粒的面向角和取向差相关。然而，实验研究局限于微米级以上尺寸，达不到纳米级甚至原子级尺度，难以深入开展材料内部微缺陷特征对材料力学性能影响的微观机理研究。由于金属材料的宏观性能源于纳米尺度的原子堆积结构和微米尺度的细观结构及其不同尺度下的变形机理，因此有必要开展纳米及以下尺度微缺陷演化研究。LI等^[8]采用分子动力学方法研究了含微裂纹和孔洞镍单晶在拉伸载荷作用下微缺陷演化机理及其邻近区域的应力变化，研究发现加载条件相同情况下，预设初始裂纹会导致较大的裂纹扩展速率，而初始孔洞缺陷则会导致更高的材料屈服应变，但是，该研究没有考虑裂纹和空洞的耦合作用对损伤的影响。JIANG等^[9]从微观角度研究了孔洞密度对镍单晶孔洞变形的位错机理影响，结果表明增加孔洞密度可以促进镍单晶的屈服。LIANG等^[10]研究了镍基单晶Ni、Ni3Al、Ni/Ni3Al界面孔洞在拉伸作用下的变形机理和孔洞的尺寸效应影响，结果发现在Ni和Ni3Al模型中，a/6[112]肖克莱不全位错首先在孔洞处成核，Ni/Ni3Al界面模型位错在界面处成核，对孔洞的尺寸效应分析发现大尺寸孔洞导致较低的屈服应力和弹性模量。

由此可见，微观缺陷的存在对单轴拉压载荷作用下镍基合金材料的宏观力学性能有明显影响。然而，晶体晶向和晶界的存在会对材料中微裂纹的扩展与孔洞的演化产生影响^[11-12]，并且当晶界为扭转晶界时，扭转晶界的扭转角的差异会造成材料力学性能的差异^[13-16]。已有一些学者针对晶向与晶界对镍基合金中微裂纹的扩展与孔洞的演化做了相关研究。SUNG等^[17]通过分子动力学研究了拉伸载荷作用下晶向对含预设裂纹镍单晶材料裂纹扩展的影响，研究表明裂纹在[111]晶向时，纳米镍单晶具有最高的临界应力与临界应变。GHOSH等^[18]通过分子动力学研究了不同晶向镍单晶在裂纹附近的变形机制，发现在相同的加载情况下，位错在达到临界应力之前发射并阻碍了裂纹的扩展，不同的晶向发射位错各不相同，这是由于不同晶向的镍基单晶边缘位错的形核和交叉滑移的影响。YUE等^[19]通过分子动力学研究了不同晶向镍单晶在拉伸载荷作用下的孔洞演化行为，结果表明晶向为[111]断裂应变最大，表明初始孔洞相同情况下[111]晶向的镍单晶具有很好的延展性。ZHANG等^[20]通过分子动力学研究了镍三晶晶界交接处孔洞生长的晶向相关性，由于滑移发生在具有较大施密德因子滑移系上，使得镍三晶的孔洞生长具有明显的晶向依赖性，滑移方向在不同的晶向存在明显差异。同时，已有学者围绕扭转晶界开展了扭转角对其裂纹扩展的影响研究。ZHANG等^[21-22]开展了扭转角对(010)扭转晶界的纳米镍双晶薄膜晶界处裂纹扩展的影响研究，发现扭转角增加引起了不全位错密度增加，导致了裂纹扩展速率增大。此外，他还研究了扭转角对纳米镍双晶中预设裂纹穿晶行为的影响，研究表明存在一个临界扭转角阻止裂纹到达晶界处后继续扩展。

综上所述，已有研究主要集中在晶界和晶向对裂纹扩展或者孔洞演化的影响，对于裂纹与孔洞耦合作用的研究集中在单晶材料^[23-24]。而针对含有扭转晶界纳米镍双晶中同时存在裂纹和孔洞的机理研究相对缺乏，因此有必要对此开展深入机理研究。为了探究晶向和扭转晶界扭转角对镍基合金材料中微缺陷演化的影响，本文以含扭转晶界的纳米镍双晶为研究对象，利用分子动力学方法研究拉伸作用下其扭转晶界的扭转角和晶向对纳米镍双晶中裂纹扩展和孔洞变形过程的影响。

1  计算方法

1.1  计算模型

ZHANG等^[21]研究了单一晶向下镍双晶扭转晶界扭转角对裂纹扩展的影响。为了研究扭转晶界的扭转角和晶向对纳米镍双晶中裂纹扩展和孔洞变形过程的影响，本文对其模型进行改进，在其基础上增加了两个孔洞^[24]。图1所示为用来模拟扭转角和晶向对纳米镍双晶扭转晶界裂纹和孔洞演化进程影响的镍双晶示意图。镍属于面心立方(FCC)结构晶体，镍的晶格常数a=3.52 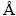。在本模拟中，对于所有的模型，其大小为50a×50a×10a。晶粒A的晶向所组成的笛卡尔坐标系如表1所示。晶粒B的晶向是通过绕着y轴旋转扭一定转角θ确定，由于FCC晶体的对称性，θ的取值分别是0°、14°、45°。在镍双晶的左边缘预设一个大小为15a× 2a×10a的边缘缺口。并在晶粒A和晶粒B中各预设一个半径为5a的圆柱形孔洞。

表1  不同晶向晶粒A的笛卡尔坐标系取向

Table 1  Cartesian coordinate system orientation of grain A with different orientations

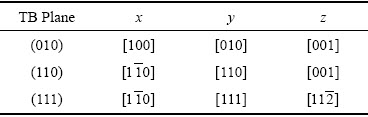
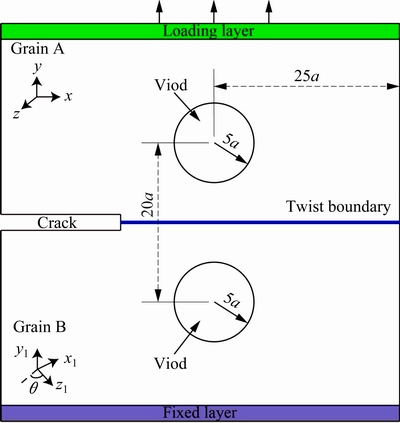
图1  含有扭转晶界和双孔洞的纳米镍双晶原子模型示意图

Fig. 1  Schematic diagram of nano-nickel bicrystal atom model with twist boundaries and double void

1.2  分子动力学方法

在本研究中，所有的模拟都是由分子动力学模拟软件LAMMPS^[25]完成。在整个模拟过程中，3个方向的边界都运用非周期性边界。整个模拟过程包含两个过程。首先，模型在温度10 K下进行驰豫，整个驰豫过程在NVT系综下进行5 ps，采用NOSE^[26]提出的方法对温度进行控制，使其达到能量最低的稳定状态。接下来，在如图1所示的加载端进行速度加载，应变率为2×10⁹ s^-1。所有的模拟都在温度为10 K的环境下进行，以消除另外两个方向上的热效应。整个模型的变形过程在NVE系综下进行。

采用FOILES等^[27]提出的嵌入原子法(EAM)势函数来描述镍原子之间的相互作用。EAM势可以表示为

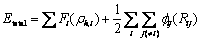            (1)

式中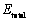：为系统总能量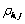；为其它原子在原子i处的电子云密度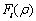；为将原子i嵌入电子云密度背景为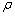的背景中所需要的能量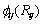；是距离为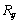的原子i与原子j之间的核对核斥力，值得注意的是，F_i只取决于原子i的元素并且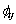只取决于原子i和原子j的元素。如上所述，电子的密度由原子的叠加来近似，即

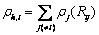                             (2)

式中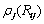：是由原子j提供的电子密度。

本文利用可视化软件OVITO^[28]对每个原子周围环境进行分析和分类，并对模拟过程中的各种变形机制进行识别。采用公共领域分析方法^[29](CNA)来实现MD模拟结果中的镍双晶晶中缺陷的可视化；该方法能够准确区分原子所处环境，并根据局部结晶分类，来实现对原子颜色进行标定。采用位错分析(DXA)^[30]来实现位错密度的收集和位错发射的可视化。

2  结果和讨论

2.1  扭转角对含孔洞与裂纹镍双晶演化的影响

2.1.1  变形过程

图2所示为具有不同扭转角的含(010)扭转晶界纳米镍双晶模型的微观变形过程原子构型图。如图2(a)所示，扭转角θ为0°时，随着应变的增加，裂纹尖端发生了一定程度的钝化，孔洞也逐渐长大。在应变达到0.14时，裂纹和晶粒B中的孔洞处出现明显的滑移；在应变达到0.25时，这些滑移导致了晶粒B中的孔洞与预设裂纹之间出现严重的塑性变形；随着塑性变形的加剧，在应变达到0.275时，这些滑移造成晶粒B中的孔洞与裂纹之间的断裂。随着加载的继续进行，在应变达到0.3时，晶粒B孔洞右侧的滑移所造成的塑性变形使镍双晶在孔洞右侧出现新裂纹并开始沿着滑移带扩展。当扭转角θ增加到14°时，如图2(b)所示，在变形的开始阶段，裂纹尖端发生了轻微的钝化。随着应变的增加，在应变达到0.14时，晶粒A中的孔洞与裂纹之间出现了滑移，并由于滑移的出现使得镍双晶薄膜在此处出现了较为严重的塑性变形，使得晶粒A中的孔洞处出现了新裂纹并扩展。如图2(c)所示，当扭转角θ为45°时，裂纹尖端未发生如θ为0°和14°时类似钝化并且预设裂纹会沿着晶界进行扩展。由于晶界处的应力集中，整个镍双晶模型的塑性变形主要集中在晶界处。在应变达到0.25时，整个镍双晶右侧出现了新的裂纹并沿着晶界进行了扩展，最终导致模型在晶界处发生完全断裂。对比图2(a)、(b)和(c)可知，随着扭转角的增加，预设裂纹裂尖的钝化越来越轻，塑性变形也逐渐向晶界处集中，整个镍双晶的断裂也由最初的孔洞生长主导转变为裂纹沿晶界扩展主导。在ZHANG等^[21]的研究中，在不存在孔洞的情况下，裂纹的扩展速率随着扭转角度的增加而增加，因此，随着扭转角度的增加，裂纹扩展越来越容易，这与本文得到的结果相符合。同时，本文的研究增加了孔洞，并且发现孔洞的存在对裂纹的扩展产生了影响。LIU等^[23]研究了裂纹与孔洞的相互作用，发现在裂纹的扩展过程中，孔洞对裂纹的扩展存在一定的影响，裂纹会逐渐靠近孔洞并与孔洞相汇集。吕斐等^[31]通过XFEM模拟了不同位置的孔洞对裂纹扩展的影响，并发现孔洞对于裂纹的扩展有一定的“吸引”作用。本文研究发现，在扭转角度较低时，由于裂纹的扩展受到一定的阻碍，因此孔洞的影响变得的更加明显。

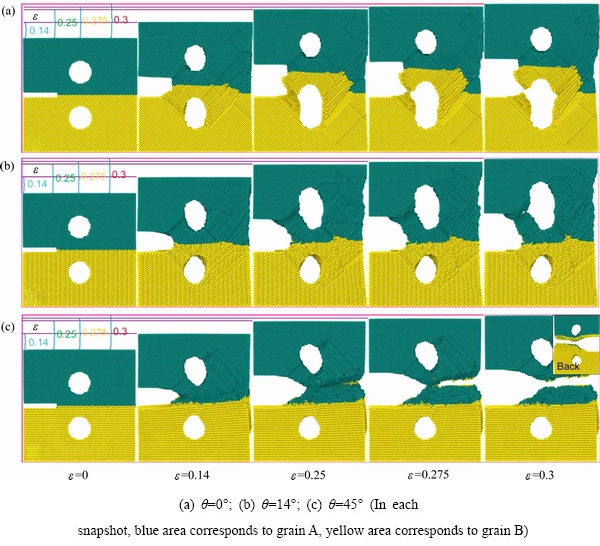
图2  含(010)扭转晶界的纳米镍双晶的演化过程

Fig. 2  Evolution process of nano-nickel bicrystals with (010) twist boundary

2.1.2  角度影响的微观机理

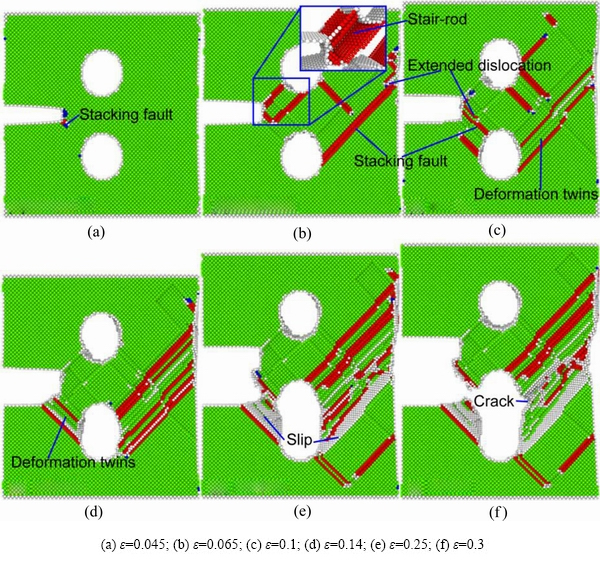
图3  含(010)扭转晶界的纳米镍双晶扭转角为0°时缺陷演化微观原子构型图

Fig. 3  Microscopic atomic configuration of defect evolution of nano-nickel bicrystals with (010) twisted grain boundaries at twist angle of 0° (the red atoms are HCP atoms, the blue atoms are BCC atoms, and the green atoms are FCC atoms, the same below)

图3所示为含有(010)扭转晶界扭转角为0°时镍双晶模型随着应变增加的微观原子构型图。WU等^[32]研究了镍单晶中边裂纹在[010]方向拉伸下扩展，发现温度在300K时，裂纹向前扩展缓慢，在裂尖处发生钝化和产生滑移。同样地，如图3(a)所示，在应变达到0.045时，在裂纹前端{111}密排面出现位错形核发射，并分别向晶粒A和晶粒B内部扩展至孔洞边界，最终被孔洞边界吸收。在应变达到0.065时，晶粒A中出现如图3(b)所示的由领先位错形成的压杆位错，同时在预设裂纹裂尖处出现向晶粒B攀升的堆垛层错。由于压杆位错比单一的堆垛层错稳定，晶粒A中的位错并未像晶粒B中的位错不断地形核发射，因此，裂尖与晶粒A中孔洞之间未出现明显的滑移，而裂尖与晶粒B中孔洞之间则出现滑移；同时，晶粒B中堆垛层错在扩展位错的作用下形成变形孪晶。变形孪晶的出现和滑移的逐渐加重使得此处出现了严重的塑性变形(见图3(e))，这些塑性变形引起孔洞长大并最终导致此处的断裂(见图3(f))。如图3(b)所示，在压杆位错形成的同时，晶粒A中孔洞右侧形成了堆垛层错并发射，这些堆垛层错的形核和发射使得晶粒A中的孔洞出现了一定的长大；直到应变到达0.14时，此处未出现新的位错并发射，晶粒A中孔洞便停止长大。在应变为0.065时，晶粒B中孔洞右侧的堆垛层错在扩展位错的作用下逐渐形成变形孪晶，并在应变达到0.1时(见图3(c))，完全形成变形孪晶。ZHOU等^[33]的模拟结果中同样在裂纹与孔洞之间出现了变形孪晶。变形孪晶的形成以及滑移(见图3(e))的持续进行使得此处出现明显的塑性变形，并随着之后此处的位错形核与发射，让此处的塑性变形更加严重，严重的塑性变形使得此处出现了大量的无序原子。这些无序原子的原子间作用力被破坏从而使得这些无序原子在拉应力的作用下形成了新裂纹，如图3(f)所示。ZHANG等^[34]通过实验观察到裂纹扩展过程中裂纹的向前扩展主要是由于裂尖的滑移导致。

图4所示为含有(010)扭转晶界扭转角为14°的镍双晶模型随应变增加的微观原子构型图。如图4(a)所示，在加载的最初阶段，扭转晶界处含有大量的原始位错和无序原子，这些无序原子和原始位错成为了新位错的发射源，使得在之后的演化中从晶界处发射了大量的位错。如图4(b)所示，在应变为0.06时，晶界和孔洞处发射的大量位错使晶界发生迁移，并在应变达到0.14时，使得扭转晶界消失(见图4(c))，因此晶界效应也同时消失了。晶粒A中孔洞与预设裂纹之间出现堆垛层错的形核和发射，使得此处出现大量的无序原子(见图4(c))，并随着加载的持续进行，此处出现明显的塑性变形(见图4(d)红色矩形区域)，并产生大量的无序原子。如图4(e)所示，这些无序原子在拉应力的作用下形成了新的裂纹，并随着应变的增加而向前扩展。如图4(d)所示，晶粒A中孔洞右侧出现位错的形核和发射，其中上方的堆垛层错形成相对稳定的压杆位错；下方位错的不断形核和发射让此处明显滑移，随着应变的增加，滑移越来越严重(见图4(f))，可以预见此处会出现新的裂纹并发生断裂。裂纹在加载初期随着晶界处的位错形核和发射向前扩展了少许，但随着晶界的消失和裂尖处位错的大量堆积(见图4(d)蓝色圆形区域)，裂纹的扩展出现阻碍。

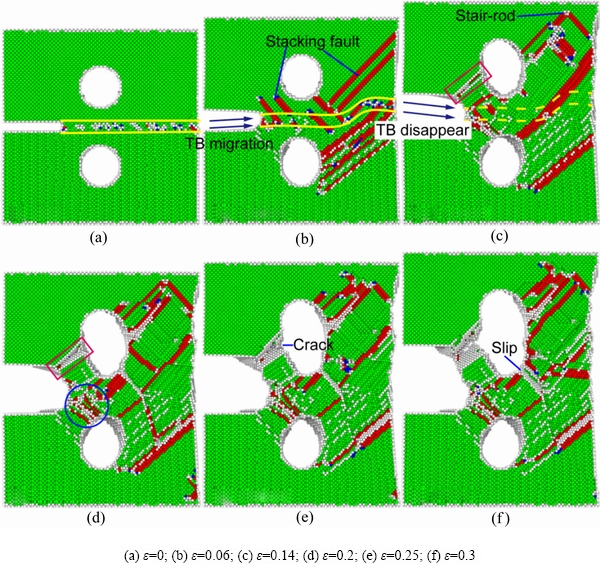
图4  含(010)扭转晶界的纳米镍双晶扭转角为14°时缺陷演化微观原子构型图

Fig. 4  Microscopic atomic configuration of defect evolution of nano-nickel bicrystals with (010) twisted grain boundaries at twist angle of 14°

图5所示为含有(010)扭转晶界扭转角为45°的镍双晶模型随应变增加的微观原子构型图。如图5(a)所示，扭转角为45°时，扭转晶界中包含了大量的无序原子；如图5(b)所示，这些无序原子在拉伸作用下，在应变达到0.06时，裂尖处开始形成堆垛层错，裂尖处位错的不断形核和发射使得裂纹在裂尖扩展(见图中蓝色箭头所示)。而随着应变的逐渐增加，晶界处出现大量的堆垛层错，如图5(c)所示，晶粒A中孔洞右上方形核发射的位错与晶界发射的位错相遇形成压杆位错。这些位错也造成了镍双晶在晶粒A中出现了明显的塑性变形，但是由于压杆位错比单一的堆垛层错稳定，因此晶粒A的变形并未在之后的加载过程中变得更加严重。由于晶界处位错的不断形核与发射使晶界处出现严重的塑性变形，晶界处的塑性变形使镍双晶晶界处出现更多无序原子，这些无序原子在拉伸作用下出现断裂(见图5(e)和(f)中黄色矩形区域)。

图5  含(010)扭转晶界的纳米镍双晶扭转角为45°时缺陷演化微观原子构型图

Fig.5  Microscopic atomic configuration of defect evolution of nano-nickel bicrystals with (010) twisted grain boundaries at twist angle of 45°

对比图3、4和5中不同扭转角的(010)扭转晶界模型可以看出，随着角度的增加，镍双晶晶界处的位错和无序原子明显增多。扭转角为14°时，整个模型的位错大量堆积在裂尖处，而裂尖的位错密度急剧升高，导致了整个镍双晶的裂纹在晶界处受到阻碍；随后由于晶界的迁移和消失，导致整个镍双晶模型的晶界效应消失，随后便与0°模型类似，整个模型的断裂由孔洞生长主导。扭转角为45°时，其中大量位错都沿晶界分布而非集中在裂尖处，使得裂纹处的位错密度相对较低，对裂纹的扩展没有抑制作用，相反还起到了一定的促进作用。这使得45°裂尖未出现明显的钝化，而是在位错的形核和发射下沿着晶界扩展。晶界处产生的大量滑移，使得晶界处出现明显的塑性变形，这也是在45°时整个模型沿晶界断裂的主要原因。

图6所示为不同扭转角(010)扭转晶界镍双晶裂纹与孔洞演化机理的示意图。如图6所示，随着扭转角的增加，镍双晶的晶界效应也逐渐变强。当扭转角为0°时，由于位错的发射和滑移的出现，晶粒B中孔洞处出现明显塑性变形，并随着孔洞的长大在孔洞与裂纹之间出现断裂，同时在孔洞处出现新的裂纹并扩展。在之前的实验研究^[35]中，新裂纹同样在孔洞的应力集中区域形成并沿着塑性变形区域向前扩展。当角度增加到14°时，镍双晶开始出现晶界效应，在晶界处位错形核和发射的作用下裂纹向前扩展；随着加载的进行，整个晶界在位错的作用下逐渐消失，晶界效应消失。整个镍双晶的变形开始集中在孔洞处，这让孔洞长大并出现新的裂纹向前扩展。当角度继续增加至45°时，晶界效应更加明显，在晶界处位错形核和发射的作用下裂纹迅速向前扩展，并在另一端出现新的裂纹；在两个裂纹同时扩展的作用下，镍双晶完全断裂。

2.2  不同晶向扭转晶界对镍双晶孔洞和裂纹演化的影响

本文分别研究了含有(010)、(110)和(111)扭转晶界的双孔洞纳米镍双晶在预设裂纹下的失效机理。为了说明晶向不同的扭转晶界对其塑性变形机制的影响，对扭转角为14°时不同晶向晶界进行分析，因为此时的扭转晶界呈现出如图7所示的非常典型的网格状晶界。

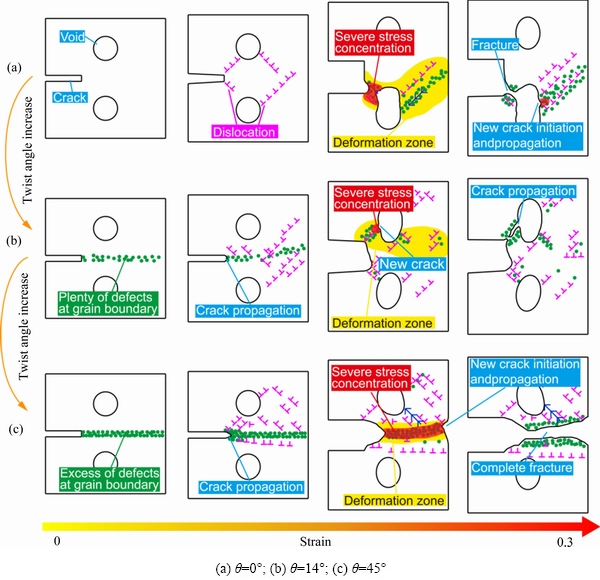
图6  不同扭转角扭转晶界对纳米镍双晶晶间裂纹与孔洞演化影响机理示意图

Fig. 6  Schematic diagram of mechanism of effect of twist boundary at different twist angles on evolution of intercrystalline cracks and voids in nano-nickel bicrystal

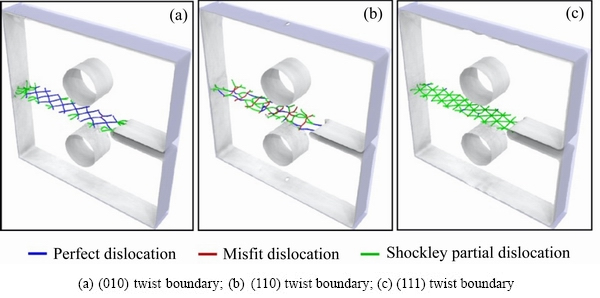
图7  不同晶向晶界处不同类型的位错分布

Fig. 7  Distribution of different types of dislocations at different orientation twist boundaries

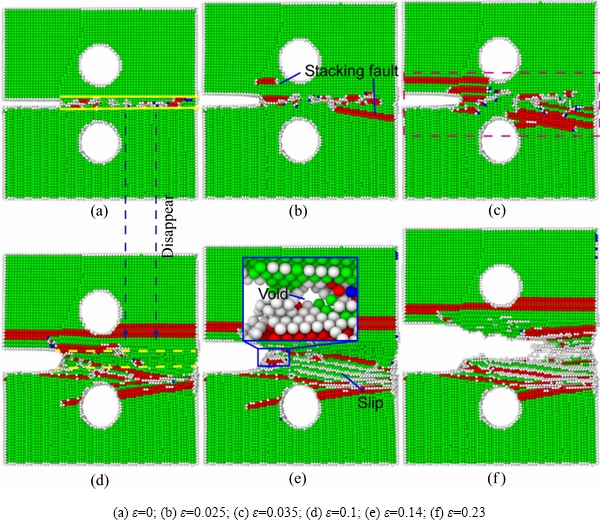
图8  含(110)扭转晶界的纳米镍双晶扭转角为14°时缺陷演化微观原子构型图

Fig. 8  Microscopic atomic configuration of defect evolution of nano-nickel bicrystals with (110) twisted grain boundaries at twist angle of 14°

图8所示为含有(110)扭转晶界扭转角为14°的镍双晶模型随应变增加的微观原子构型图。如图8(a)所示，可以观察到明显的晶界。如图8(b)所示，在应变达到0.025时，位错同时在裂尖和晶界的密排面{111}面出现并迅速向两侧攀升，也让裂纹向前扩展。如图8(c)所示，在应变为0.035时，晶界处迅速出现大量的堆垛层错，使得晶界处出现明显的塑性变形；如图8(d)所示，随着加载的继续进行，随着位错的发射和攀升使得晶界在应变为0.1时消失，晶界效应也由此消失。而裂纹前端出现的位错形核和发射，使裂纹向前扩展，同时在裂纹前端出现大量的滑移，使镍双晶模型在此处出现大量塑性变形。此处积累大量的塑性变形和应力集中使镍双晶出现大量无序原子，无序原子的原子键断裂和无序移动造成裂纹前端出现孔洞(见图8(e))。随着孔洞的长大和汇集，裂纹向前快速扩展(见图8(f))，并最终完全断裂。ZHOU等^[33]研究了裂纹在含晶界的FCC金属铜中的扩展，发现在晶界处的裂纹尖端会出现{111}密排面的滑移，并在裂纹前出现孔洞使裂纹向前扩展，与本文模拟结果相符。

图9所示为含有(111)扭转晶界扭转角为14°的镍双晶模型随应变增加的微观原子构型图。如图9(b)所示，镍双晶最先在裂尖处出现位错形核和发射，并形成压杆位错；压杆位错的解离让裂纹向前扩展，随后在晶界处出现位错形核和发射。如图9(c)所示，预设裂纹与晶粒A中孔洞之间形核发射的堆垛层错在扩展位错的作用下转变为变形孪晶，这导致了此处出现明显的塑性变形。如图9(c)所示，镍双晶扭转晶界在位错的作用下逐渐消失，在应变达到0.14时，晶界基本全部消失，同时裂纹在位错的不断发射下向前扩展了少许。如图9(d)所示，晶粒B中的孔洞与裂纹之间的位错不断形核和发射，使得此处出现明显的滑移变形(见图9(e))，同时在裂尖出现大量的位错，位错的大量堆积阻碍了裂纹的扩展。

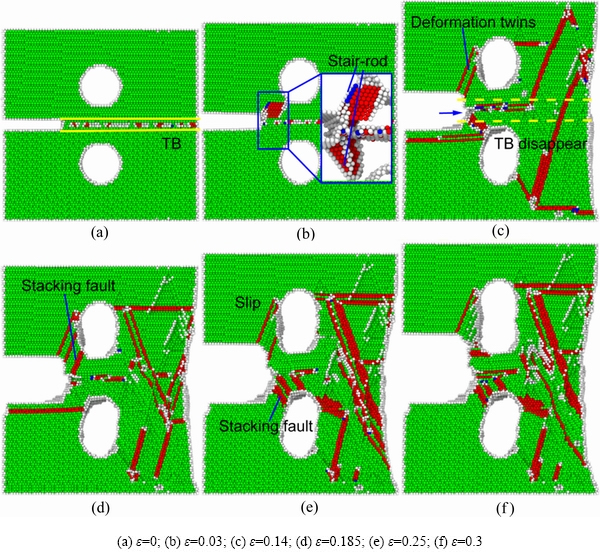
图9  含(111)扭转晶界的纳米镍双晶扭转角为14°时缺陷演化微观原子构型图

Fig. 9  Microscopic atomic configuration of defect evolution of nano-nickel bicrystals with (111) twisted grain boundaries at twist angle of 14°

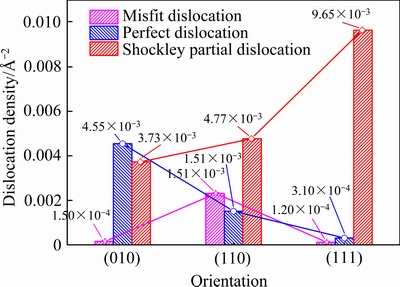
图10  不同晶向晶界处不同类型的位错密度

Fig. 10  Dislocation density of different types at grain boundaries with different crystal orientations

图10所示为在加载前刚驰豫完成时的晶界处通过DXA分析得到的原始位错的密度情况。从图4、8和9所示的含有(010)、(110)和(111)扭转晶界的镍双晶的演化过程可以发现， (110)晶界最先在晶界处发射大量的肖克莱不全位错，这是由于(110)晶界处含有大量的原始失配位错，这些失配位错就是肖克莱不全位错最好的发射源。而这些肖克莱不全位错促进了裂纹的扩展，导致(110)晶界处裂纹扩展最快，使得裂纹的扩展成为了镍双晶破坏的主要原因。而(111)晶界处加载之初晶界处的失配位错的密度非常低，而含有大量的肖克莱不全位错，而这些肖克莱不全位错与在之后的加载过程中出现的新位错造成了晶界处远胜于(110)晶界处的位错堆积，这些位错堆积造成了最后(111)晶界处存在的裂纹扩展被阻碍，使得此时孔洞的演化变成了镍双晶破坏的主要原因。(010)晶界和(111)晶界的失配位错密度比(110)晶界要低，因此(010)晶界处形核发射的位错明显要少于(110)晶界和(111)晶界，因此镍双晶的断裂明显比(110)晶界要难。(110)扭转晶界镍双晶在应变为0.26时便发生完全断裂，而(010)和(111)扭转晶界镍双晶在应变达到0.3时也未完全断裂。由此可见，裂纹在(110)扭转晶界镍双晶中最易扩展，在(010)和(111)扭转晶界镍双晶中较扩展。

基于上述分析，可以发现在扭转角相同的情况下，各个晶向晶界处的原始位错密度各不相同，导致镍双晶在之后的演化中位错的形核和发射不同。同时在实验中观察到晶界处的裂纹扩展行为在很大程度上取决于晶体取向^[36-38]。图11所示为(010)扭转晶界、(110)扭转晶界和(111)扭转晶界镍双晶在扭转角为14°时裂纹和孔洞演化机理的示意图。扭转角为14°的镍双晶在拉伸作用下晶界逐步消失，但是在晶界消失之前，晶界处形核并发射了大量的位错，产生明显滑移并形成了应力集中。由图4、8和9可以看出，(110)扭转晶界镍双晶最先在应变为0.025时在晶界处和裂尖位置发射位错，(111)扭转晶界镍双晶和(010)扭转晶界镍双晶则在应变0.025之后发射位错。如图11所示，在(111)扭转晶界镍双晶中，塑性变形区域远大于(110)扭转晶界一含(010)扭转晶界镍双晶中的塑性变形区域，而(110)扭转晶界处的塑性变形的集中和加剧使塑性变形区域内出现明显的应力集中，导致在裂纹前端出现孔洞并随着演化而断裂。含(010)扭转晶界镍双晶的塑性变形区域主要集中在孔洞处而非晶界处，这让孔洞出现明显的长大并最终形成新裂纹。(110)扭转晶界镍双晶晶界处的位错形核和发射较多，孔洞处较少位错形核和发射。而(010)扭转晶界和(111)扭转晶界镍双晶的孔洞处便有大量的位错形核和发射，使得这两个镍双晶的孔洞出现明显的长大，导致两者塑性变形区域不仅局限于晶界处。

在之前的研究中，SUNG等^[17]研究了[100]、[110]和[111]晶向下FCC铜单晶裂纹在拉伸作用下的扩展情况，发现不同晶向下的断裂应力与断裂应变有关，由大到小为[111]、[100]、[110]，这与本文得到的结果一致。同样地，WANG等^[19]研究了[100]、[110]和[111]晶向下FCC镍单晶中单孔洞在拉伸作用下的孔洞变形，发现在[111]晶向下镍单晶具有最好的延展性。本文中，在[111]晶向下，由于裂纹扩展阻碍，同时孔洞的断裂应变最大，因此最不容易发生断裂。这与文献[17, 19]的研究结果相符。COURA等^[39]通过高分辨率的透射电子显微镜观察FCC金属[100]、[110]和[111]方向上的断裂应变，发现[110]的延展性最低，这也与本文研究结果相符。

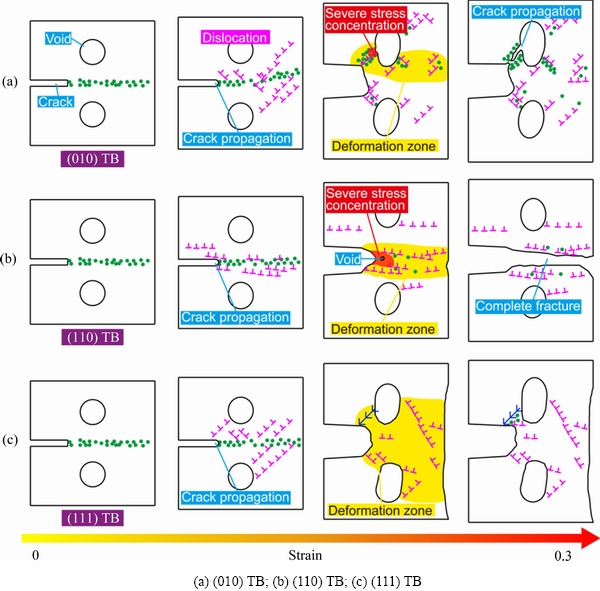
图11  不同晶向扭转晶界对纳米镍双晶晶间裂纹和孔洞演化影响机理示意图

Fig. 11  Schematic diagram of mechanism of effect of twist boundary in different orientation on evolution of intercrystalline cracks and voids in nano-nickel bicrystal

3  结论

1) 不同的扭转角决定了扭转晶界处存在不同的失配位错密度，而晶界处的失配位错密度决定了在整个拉伸过程中镍双晶的位错形核和发射。对于含有(010)扭转晶界镍双晶，在扭转角为0°时，镍双晶的断裂由孔洞的长大变形主导；在扭转角增加到14°时，晶界效应逐渐明显，裂纹也沿晶界向前扩展少许，随着加载的进行，晶界在位错的不断形核和发射过程中发生迁移并完全消失，使得晶界效应消失，因此镍双晶的断裂变为由裂纹扩展与孔洞长大共同作用。当扭转角增加到45°时，晶界处的大量失配位错引起大量的位错形核和发射，导致塑性变形主要发生在晶界附近，让裂纹沿晶界向前扩展，并在晶界另一端出现新裂纹，最终导致整个镍双晶的断裂。

2) 对比在相同扭转角时不同晶向扭转晶界的镍双晶模型，由于(110)扭转晶界镍双晶晶界处存在的失配位错远多于(010)和(111)扭转晶界镍双晶，使得(110)扭转晶界镍双晶更容易生成位错，导致其断裂主要由预设裂纹沿晶界扩展。含(010)扭转晶界和(111)扭转晶界镍双晶由于在晶界处存在大量的原始肖克莱位错并与之后形成的位错堆积，导致其位错密度相对其他晶界较高；高位错密度使得裂纹的扩展受到阻碍，而孔洞处形核和发射了大量的位错让孔洞随着加载进行逐渐长大，使得(010)和(111)扭转晶界镍双晶的断裂主要由孔洞长大导致。

REFERENCES

[1] KRUEGER D D. The development of direct age 718 for gas turbine engine disk applications[C]//LORIA E A ed. Superalloy 718: Metallurgy and Applications. Warrendale, PA : TMS, 1989: 279-296.

[2] ZHOU Yu, YE Hao-yu, RAO Si-xian. An investigation of the microstructural evolution of a service-exposed turbine blade[J]. Metallography, Microstructure, and Analysis, 2016, 5(4): 321-326.

[3] JHA S K, CATON M J, LARSEN J M. The mean vs life-limiting fatigue response of a Ni base superalloy. Part Ⅱ: Life-prediction methodology(Preprint)[R]. Metall Mater Trans A, 2008.

[4] JHA S K, CATON M J, LARSEN J M. A new paradigm of fatigue variability behavior and implications for life prediction[J]. Materials Science and Engineering A, 2006, 468: 23-32..

[5] CATON M J, JHA S K. Small fatigue crack growth and failure mode transitions in a Ni-base superalloy at elevated temperature[J]. International Journal of Fatigue, 2010, 32(9): 1461-1472.

[6] KEVINSANNY O S, TAKAKUWA O, OGAWA Y, et al. Effect of defects on the fatigue limit of Ni‐based superalloy 718 with different grain sizes[J]. Fatigue & Fracture of Engineering Materials & Structures, 2019, 42(5): 1203-1213.

[7] 张宝宁, 袁 超, 郭建亭, 等. GH4742合金疲劳裂纹扩展行为[J]. 中国有色金属学报, 2017, 27(9): 1823-1831.

ZHANG Bao-ning, YUAN Chao, GUO Jian-ting, et al. Fatigue crack growth behavior of GH4742 alloy[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(9): 1823-1831.

[8] LI Yun-li, WU Wen-ping, LI Na-nin, et al. Cohesive zone representation of crack and void growth in single crystal nickel via molecular dynamics simulation [J]. Computational Materials Science, 2015, 104: 212-218.

[9] JIANG Shu-yong, ZHANG Yan-qiu, ZHU Xiao-ming, et al. Influence of void density on dislocation mechanisms of void shrinkage in nickel single crystal based on molecular dynamics simulation[J]. Physica E, 2017, 90.

[10] WANG J P, LIANG J W, WEN Z X, et al. Atomic simulation of void location effect on the void growth in nickel-based single crystal[J]. Computational Materials Science, 2019, 160: 245-255.

[11] ZHANG Yan-qiu, JIANG Shu-yong, ZHU Xiao-ming, et al. Mechanisms of crack propagation in nanoscale single crystal, bicrystal and tricrystal nickels based on molecular dynamics simulation[J]. Results in Physics, 2017, 7: 1722-1733.

[12] KEDHAMATH A, PANWAR A S, KAPOOR R. Molecular dynamics simulation of the interaction of a nano-scale crack with grain boundaries in α-Fe[J]. Computational Materials Science, 2017, 137: 85-99.

[13] FENG Ya-xin, SHANG Jia-xiang, QIN Sheng-jian. Tensile response of (110) twist grain boundaries in tungsten: A molecular dynamics study[J]. Computational Materials Science, 2019, 159: 265-272.

[14] CHEN S D, ZHOU Y K, SOH A K. Molecular dynamics simulations of mechanical properties for Cu(001)/Ni(001) twist boundaries[J]. Computational Materials Science, 2017, 137: 85-99.

[15] PAUL S K. Effect of twist boundary angle on deformation behavior of 〈100〉 FCC copper nanowires[J]. Computational Materials Science, 2018, 150: 24-32.

[16] CHANDRA S, NAVEEN K N, SAMAL M K, et al. An atomistic insight into the fracture behavior of bicrystal aluminum containing twist grain boundaries[J]. Computational Materials Science, 2017, 130: 268-281.

[17] SUNG P H, CHEN T. Studies of crack growth and propagation of single-crystal nickel by molecular dynamics[J]. Computational Materials Science, 2015, 102: 151-158.

[18] GHOSH S, ZHANG J. Molecular dynamics based study and characterization of deformation mechanisms near a crack in a crystalline material[J]. Journal of the Mechanics & Physics of Solids, 2013, 61(8): 1670-1690.

[19] WANG J P, YUE Z F, WEN Z X, et al. Orientation effects on the tensile properties of single crystal nickel with nanovoid: Atomistic simulation[J]. Computational Materials Science, 2017, 132: 116-124.

[20] ZHANG Yan-qiu, ZHU Xiao-ming, SUN Dong, et al. Orientation dependence of void growth at triple junction of grain boundaries in nanoscale tricrystal nickel film subjected to uniaxial tensile loading[J]. Journal of Physics and Chemistry of Solids, 2016, 98: 220-232.

[21] ZHANG Yanq-iu, JIANG Shu-yong, ZHU Xiao-ming, et al. A molecular dynamics study of intercrystalline crack propagation in nano-nickel bicrystal films with (010) twist boundary[J]. Engineering Fracture Mechanics, 2016, 168: 147-159.

[22] ZHANG Yan-qiu, JIANG Shu-yong, ZHU Xiao-ming, et al. Influence of twist angle on crack propagation of nanoscale bicrystal nickel film based on molecular dynamics simulation[J]. Physica E: Low-dimensional Systems and Nanostructures, 2017, 87: 281-294.

[23] LIU T, GROH S. Atomistic modeling of the crack-void interaction in α-Fe[J]. Materials Science and Engineering A, 2014, 609: 255-265.

[24] WANG Liang, LIU Qun-feng, SHEN Sheng-ping. Effects of void-crack interaction and void distribution on crack propagation in single crystal silicon[J]. Engineering Fracture Mechanics, 2015, 146: 56-66.

[25] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19.

[26] NOSE S C. A unified formulation of the constant temperature molecular dynamics methods[J]. Chem Phys, 1984, 81(1): 511-519.

[27] FOILES S M, BASKES M I, DAW M S. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys[J]. Physical Review B, 1986, 33(12): 7983-7991.

[28] STUKOWSKI A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(1): 015012.

[29] TSUZUKI H, BRANICIO P S, RINO J P. Structural characterization of deformed crystals by analysis of common atomic neighborhood[J]. Computer Physics Communications, 2007, 177: 518-523.

[30] STUKOWSKI A, ALBE K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data [J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(8): 2131-2145.

[31] 吕 斐, 缪新婷, 周昌玉. 孔洞对单边裂纹板裂纹扩展方向的影响[J]. 南京工业大学学报(自然科学版), 2017, 39(4): 86-92, 101.

LYU Fei, MIAO Xin-ting, ZHOU Chang-yu. Effects of the hole on the crack propagation direction in single edge-cracked plate[J]. Journal of Nanjing Tech University (Natural Science Edition), 2017, 39(4): 86-92, 101.

[32] WU Wen-ping, YAO Zong-zhuan. Molecular dynamics simulation of stress distribution and microstructure evolution ahead of a growing crack in single crystal nickel[J]. Theoretical and Applied Fracture Mechanics, 2012, 62: 67-72.

[33] ZHOU Yan-guang, YANG Zhen-yu, LU Zi-xing. Dynamic crack propagation in copper bicrystals grain boundary by atomistic simulation[J]. Materials Science and Engineering A, 2014, 599: 116-124.

[34] ZHANG L, ZHAO LG, ROY A, et al.. In-situ SEM study of slip-controlled short-crack growth in single-crystal nickel superalloy[J]. Materials Science and Engineering A, 2018, 742: 564-572.

[35] LI Zhen-wei, WEN Zhi-xun, GU Shu-ning, et al. In-situ observation of crack initiation and propagation in Ni-based superalloy with film cooling holes during tensile test[J]. Journal of Alloys and Compounds, 2019, 793: 65-76.

[36] WANG Jian-heng, ANDERSON P M. Fracture behavior of embrittled F.C.C. metal bicrystals[J]. Acta Metallurgica et Materialia, 1991, 39: 779-792.

[37] BELTZ G E, Wang J S. Crack direction effects along copper/sapphire interfaces[J]. Acta Metallurgica et Materialia, 1992, 40(7): 1675-1683.

[38] WANG J S. A micromechanical model for interface crack extension in metal/ceramic bimaterial systems[J]. Acta Materialia, 1998, 46(14): 4973-4984.

[39] COURA P Z, LEGOAS S B, MOREIRA A S, et al. On the structural and stability features of linear atomic suspended chains formed from gold nanowires stretching[J]. Nano Letters, 2004, 4(7): 1187-1191.

Influence of twist angle and orientation on fracture of nano-nickel bicrystal with micro-defects

DING Jun¹, TONG Quan¹, ZHANG Sheng-lai¹, WANG Lu-sheng², HUANG Xia¹,SONG Kun¹, LU Shi-qing¹

(1. College of Mechanical Engineering, Chongqing University of Technology, Chongqing 400054, China;

2. College of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract: The molecular dynamic simulation was conducted to analyze the influences of twist angle of twist boundary (TB) and orientation on fracture of nano-nickel bicrystal with micro-defects under uniaxial tensile loading. The result shows that the twist angle and orientation determine the density of misfit dislocations at the twist boundary, affecting the nucleation and emission of dislocations in nickel bicrystal. With the increase of twist angle, the nucleation and emission of dislocation at grain boundaries gradually increase, the cracks propagate forward more quickly, and the deformation of the void becomes smaller, so that the fracture caused by void growth at 0° changes to the fracture caused by propagation of the cracks at 45°. For nano-nickel bicrystal with twist boundaries in different crystal directions, (110) twist boundary nickel bicrystal has a greater crack growth rate compared to (010) and (111) twist boundary nickel bicrystals, the concentration of plastic deformation also makes the void growth not obvious, and it is completely fractures before the strain reaches 0.3. However, the crack propagation of the (110) and (111) twist boundary nickel bicrystals is more difficult, and the void growth is more obvious. And the (110) and (111) twist boundary nickel bicrystals not completely fracture when the strain reaches 0.3, so they have better ductility and malleability.

Key words: nickel bicrystal; molecular dynamics; twist boundary; twist angle; orientation; voids; crack

Foundation item: Project(U1530140) supported by NSAF; Project(CSTC2017JCYJAX0357) supported by the Foundation and Frontier Research of Chongqing, China; Project(6142A0501020217) supported by the Foundation of National Key Defense Laboratory of Computational Physics, China; Project (KJQN202001126) supported by the Science and Technology Research Project of Chongqing Education Commission, China; Project(cstc2020jcyj-msxmX0286) supported by the General Project of Chongqing Natural Science Foundation, China

Received date: 2020-08-08; Accepted date: 2020-12-04

Corresponding author: DING Jun; Tel: +86-23-62563039; E-mail: dingjunawen@126.com

(编辑  何学锋)

基金项目：国家自然科学基金委员会与中国工程物理研究院联合资助项目(U1530140)；重庆市基础与前沿计划资助项目(CSTC2017JCYJAX0357)；计算物理国防科技重点实验室基金资助项目(6142A0501020217)；重庆市教育委员会科学技术研究项目(KJQN202001126)；重庆市自然科学基金资助项目(cstc2020jcyj-msxmX0286)

收稿日期：2020-08-08；修订日期：2020-12-04

通信作者：丁  军，教授，博士；电话：023-62563039；E-mail：dingjunawen@126.com