饱和-非饱和渗流条件下降雨对粗粒土路堤边坡稳定性的影响

曾铃¹，付宏渊¹，何忠明²，贺炜¹，周功科²

(1. 长沙理工大学 土木与建筑学院，湖南 长沙，410004；

2. 长沙理工大学 交通运输工程学院，湖南 长沙，410004)

摘要：为了研究粗粒土路堤在降雨条件下的入渗过程及稳定性，提出一种基于饱和-非饱和渗流及非饱和抗剪强度理论的路堤边坡稳定性分析方法。利用该方法对算例边坡的降雨入渗过程及瞬态稳定性进行研究。研究结果表明：降雨将引起路堤地下水位升高，降雨停止后地下水位由于雨水出渗而降低；路堤边坡表层受降雨入渗影响，区域基质吸力丧失(甚至变为正值)，体积含水率增大，在降雨停止后都逐渐减小；在降雨过程中，路堤边坡安全系数缓慢降低，塑性区随地下水位线沿坡脚向上延伸，面积相应增大；在降雨停止后，在雨水出渗及基质吸力恢复的共同作用下，路堤边坡安全系数得到一定程度恢复。

关键词：饱和-非饱和渗流；地下水位线；基质吸力；塑性区；安全系数

中图分类号：TU416          文献标志码：A         文章编号：1672-7207(2014)10-3614-07

Impact of rainfall on stability of granular soil embankment slope considering saturated-unsaturated seepage

ZENG Ling¹, FU Hongyuan¹, HE Zhongming², HE Wei¹, ZHOU Gongke²

(1. School of Civil Engineering and Architectural, Changsha University of Science & Technology, Changsha 410004, China;

2. School of Traffic & Transportation Engineering, Changsha University of Science & Technology, Changsha 410004, China)

Abstract: In order to study the infiltration process and stability of granular soil embankment in the condition of rainfall, a method of analyzing the slope stability of embankment was put forward, which was based on the theory of saturated-unsaturated seepage and unsaturated shear strength. The rainfall infiltration process and transient stability of an example slope were researched with this method. The results show that the groundwater level of embankment increases because of the rainfall and decreases because of the rainwater seeping out after rainfall. The regional matric suction of slope surface affected by rainfall infiltration loses (even becomes positive) and volume water content increases, and then gradually decreases after rainfall. During the rainfall, the safety factor of embankment slope gradually decreases. The plastic zone extends upward along the foot of slope with the groundwater level, and the area of plastic zone increases. With the combined actions of the recovery of regional matric suction and the rainwater seeping out after rainfall, the safety factor of embankment slope recovers to some degree.

Key words: saturated-unsaturated seepage; underground watertable; matric suction; plastic zone; safety factor

在我国南方山岭地区修建高速公路，由于受地形限制，公路路堤填方高度大，施工难度高，特别是路堤填土压实度与均匀性难以按照规范加以控制：因此，对于压实度未达到规范要求的路堤，在强度大、持续时间长的雨水入渗的影响下极易发生滑移破坏。在日本，每年由于降雨导致的边坡失稳达上万个^[1]。而在我国，路堤边坡失稳也多发生在雨季^[2]。可见高速公路路堤边坡的失稳与雨水的入渗有密不可分的关系。近年来，人们对降雨引起路堤边坡失稳的机理及影响因素开展了许多研究，如：邱文^[3]基于饱和-非饱和渗流数学模型，分析了雨水入渗作用下土体中的含水率、基质吸力的变化规律，并对降雨过程中边坡安全系数的变化进行了计算，认为基质吸力的变化是引起边坡失稳的主要原因；邹维列等^[4]在分级加载和人工降雨条件下，完成了不同压实度时路堤的室内模型试验，获得了非饱和路堤对加载和降雨入渗的响应规律；李佳等^[5]通过试验手段得到了水在非饱和黄土边坡中的渗透范围，分析了含水率的变化规律，并讨论了暂态饱和区的形成机制；牛文明等^[6]系统分析了饱和土与非饱和土渗透特性，并以此为基础提出了非饱和土渗透特性试验方法，为测定非饱和土渗透系数提供了参考。人们尽管认识到降雨是引起路堤边坡失稳的重要影响因素，但由于降雨入渗过程复杂，很难找到一种能够同时考虑降雨过程中基质吸力、体积含水率、岩土物理力学参数、岩土体重度同时变化的路堤稳定性计算方法。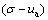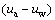目前，基于有限元软件对边坡降雨入渗的模拟是建立在对降雨边界的简化和结合饱和-非饱和渗流计算理论展开的^[7-11]，在分析得到边坡体内基质吸力分布及暂态分布后，结合非饱和抗剪强度理论考虑和的共同作用(其中，σ为土体中的正应力，u_a为孔隙压力，u_w为孔隙水压力)，并利用极限平衡方法对边坡稳定性进行计算。该方法思路清晰且便于实现，但主要缺陷在于只考虑了边坡体内基质吸力的变化，而未考虑由于降雨入渗引起的边坡岩土体重度增加、材料软化以及雨水入渗后的流固耦合过程。一些研究者认识到这一问题，采用自行编制计算程序的方法加以解决，但由于其计算程序编制复杂以及运用的针对性较强，很难得到广泛推广^[12]。为此，本文作者基于饱和-非饱和渗流理论计算路堤边坡在降雨入渗过程中的孔隙水压力变化，提出一种既能真实反映降雨入渗过程中边坡体内孔隙水压力与土体重度的变化，又能考虑非饱和抗剪强度理论结合“双参数”变化的饱和-非饱和路堤边坡稳定性分析方法，并结合算例对降雨入渗作用下路堤边坡的失稳变形模式进行探讨，以便为研究路堤高边坡在降雨作用下的边坡变形失稳特征提供一种行之有效的途径，为此类路堤边坡失稳的预测和采取合理的支护措施提供参考。

1  饱和-非饱和渗流计算原理

在降雨条件下的路堤边坡渗流场分析中，饱和区与非饱和区的地下水的流动是相互联系的，需将两者统一起来研究，可将此表述为饱和-非饱和渗流问题，为此，以土水势为因变量建立统一的控制方程。饱和-非饱和渗流与饱和渗流一样，满足达西定律土体内非恒定渗流，其偏微分方程形式如下^[13]：

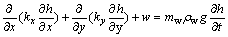     (1)

式中：h为岩土体的总水头高度；k_x和k_y分别为x和y方向的渗透系数；w为源汇项；m_w为比水容量；ρ_w为水的密度；g为重力加速度；t为时间。

岩土体非恒定渗流有限元方程由下式描述：

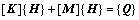           (2)

式中：[K]为单元特征矩阵；[M]为单元质量矩阵；{Q}为节点流量向量；{H}为恒定流节点水头向量。

有限元方程求解结合以下边界条件进行：

           (3)

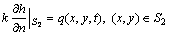        (4)

式中：S₁为已知水头边界；S₂为已知流量边界。

非恒定渗流分析的初始条件为

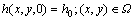          (5)

在降雨入渗作用下的非饱和渗流计算中，岩土体渗透性与饱和土体体积含水率和基质吸力有密切关系。前人在缺乏现场试验资料的情况下采用较常用的确定渗透系数的方法即经典公式Van Genuchten或Fredlund模型进行拟合^[14]。本文采用Van Genuchten模型进行拟合，模型表达式为：

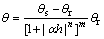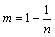；；0＜m＜1    (6)

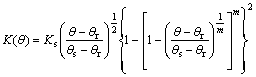   (7)

式中：θ为体积含水率(cm³/cm³)；θ_r为残余含水率(cm³/cm³)；θ_s饱和含水率(cm³/cm³)；H 为负压；K_s为饱和渗透系数；α，m和n为土水特征曲线形状参数。

2  基于饱和-非饱和渗流及非饱和抗剪强度理论的路堤边坡稳定性分析方法

2.1  基于非饱和抗剪强度理论的Mohr-Coulomb破坏准则的推导

库仑于1776年提出了抗剪强度τ_f计算公式^[15]：

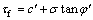              (8)

其中：σ为正应力；c′为有效黏聚力；φ′为有效摩擦角。式(8)表明材料的抗剪强度与作用于该平面上的正应力有关，引起材料破坏的不是最大剪应力，而是在某个平面上的τ-σ最危险组合。该公式主要适用于不考虑地下水位线以上基质吸力时岩土体抗剪强度的计算，而当需要考虑地下水位以上基质吸力时，目前采用由Ho等^[16]提出的非饱和抗剪强度公式：

     (9)

式中：u_w为孔隙水压力；u_a为孔隙气压力，本文在稳定性分析时认为孔隙气压力为大气压力，即u_a=0 kPa；φ^b为基质吸力增加引起抗剪强度增加的曲线的倾角，它是基质吸力的函数，本文根据经验值取14°。

将式(9)按照u_a=0和φ^b为常数进行整理得

   (10)

式中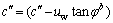：，为非饱和等效黏聚力。

式(10)则为考虑非饱和抗剪强度理论中基质吸力存在的修正Mohr-Coulomb破坏准则。

2.2  考虑降雨入渗及非饱和抗剪强度的路堤边坡稳定性分析流程

考虑降雨入渗条件下的路堤边坡稳定性计算是在二维饱和-非饱和计算软件Seep/W及FLAC3D软件平台上实现的。首先，建立二维有限元模型进行二维饱和-非饱和渗流分析；然后，基于二维模型建立三维等效模型，通过在FLAC3D中编写用户子程序，将降雨入渗过程中某一时刻的孔隙水压力导入FLAC3D等效计算模型，同时，编写相应的程序按式(10)中的c″对莫尔库仑准则中的黏聚力c′进行等效赋值，并设置孔隙水压力大于0 kPa的区域土体重度为γ_sat，对于孔隙水压力小于0 kPa的区域则将土体重度在干重度γ_d与饱和重度γ_sat进行线性插值赋值。运用强度折减法对该时刻的边坡稳定性进行计算，计算流程如图1所示。

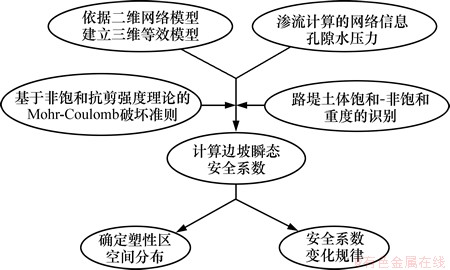
图1  路堤边坡稳定性计算流程

Fig. 1  Calculation process of embankment slope stability

3  降雨对粗粒土路堤边坡稳定性影响实例分析

3.1  数值模型及相关参数

在建广西六寨至河池高速公路K19+133断面路面宽60 m，填方高度为12 m，路堤边坡坡度为30°。路堤中使用典型的土-石(崩解完成后的炭质泥岩)混填粗粒土填料，由于路堤两侧对称，故选取半剖面作为研究对象。路堤典型剖面二维有限元网格如图2所示。为了研究路堤在降雨入渗条件下的渗流特征，设置测点①~⑤为研究辅助特征点，位于路堤坡面以下 1 m处。计算模型单元数量为4 405个，节点数量为4 536个。为了保证计算精度，通过设置辅助线的方法将网格划分为四边形单元。

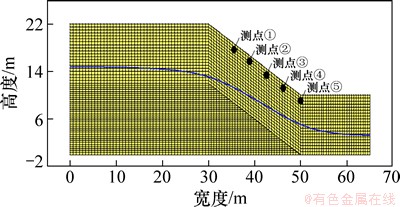
图2  路堤典型剖面二维有限元网格

Fig. 2  2D finite element model of typical cross section of embankment

渗流边界条件：模型底部、两侧铅直位置和路堤路面设置为不透水边界，路堤坡面和坡脚水平面设置为单位流量边界。

渗流初始条件：根据对路堤坡面及坡脚多个位置的钻孔取样资料，设置如图2所示的初始地下水位进行稳态流计算，以此计算结果作为边坡初始渗流场。

渗流水力学模型：采用各向同性达西渗流模型。

渗流计算水力学参数：根据现场获取原状土样进行室内饱和渗流试验，测得饱和渗透系数为4.6×10^{-7 m/s}，饱和体积含水率为0.1。由当地气象资料可知，广西六寨地区有历史记录以来的最大日降雨量为350 mm，经换算为单位降雨强度q=4.05×10^{-6 m/s}。雨水入渗属于典型的饱和-非饱和瞬态渗流。边坡非饱和区渗透系数为非饱和渗透系数，本文采用式(6)和(7)所示的Van Genuchten模型对非饱和区渗透系数进行拟合，渗透系数及含水量随基质吸力变化见图3和图4。根据现有研究成果，路堤中基质吸力最大值一般不大于100 kPa，因此，本文最大基质吸力取150 kPa，以保证实际渗透系数及含水量在拟合范围内。

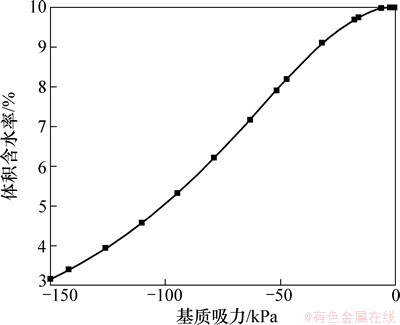
图3  体积含水率θ与基质吸力p关系曲线

Fig. 3  Relationship between water content and pressure

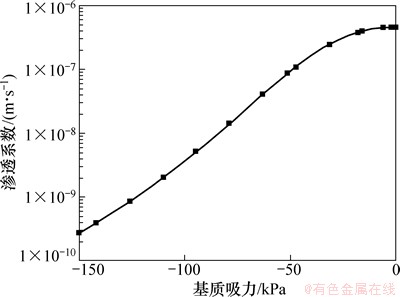
图4  渗透系数k与基质吸力p关系曲线

Fig. 4  Relationship between conductivity and pressure

3.2  饱和非饱和渗流计算结果分析

图5和图6所示分别为边坡在降雨及降雨停止后地下水位变化过程示意图。由图5和图6可知：在降雨过程中，路堤边坡地下水位随着降雨持续时间的延长而逐渐升高，但升高速率缓慢降低，特别是当地下水位升高到与路堤中部原地下水位持平时速率降低明显。这是由于这时靠近路堤坡面附近较高地下水区域与路堤中部位置形成一定的水头差，因此，入渗雨水向路堤中部补给，从而导致路堤坡面附近地下水位升高缓慢的同时引起路堤中部地下水位也有一定升高；此外，路堤内水位升高导致路堤内部地下水与边坡坡面水力梯度增大，从而引起路堤边坡表面雨水出渗量增大。降雨停止后，由于没有雨水入渗的持续补给，路堤内地下水位显著下降，具有下降速率逐渐减缓的趋势，这是路堤内水力梯度减小的主要原因。

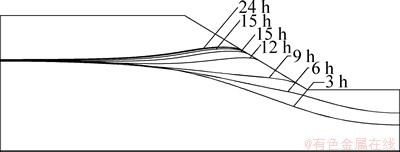
图5  降雨过程中路堤边坡地下水位变化规律(降雨24 h)

Fig. 5  Change law of underground watertable of embankment slope during rainfall (Rainfall duration is 24 h)

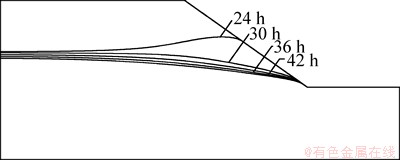
图6  降雨结束24 h内路堤边坡地下水位变化规律

Fig. 6  Change law of underground watertable of embankment within 24 h after rainfall

本文只列出边坡在降雨持续24 h后路堤内孔隙水压力分布，如图7所示。为了便于阐述路堤在降雨过程中孔隙水压力及体积含水率的变化，列出路堤表层特征测点①~⑤孔隙水压力与体积含水率在降雨过程中的变化规律(分别见图8和图9)。由图8可知：特征测点孔隙水压力随着降雨持续入渗由负值逐渐增大，降雨停止后随着雨水的出渗，孔隙水压力逐渐降低，坡顶降低速率大于坡脚降低速率，与特征点高程呈正比。由图9可知：边坡特征点体积含水率与孔隙水压力具有相同的变化趋势；当雨水入渗区域达到饱和时，体积含水率为饱和含水率，当雨水出渗后饱和区变为非饱和区，体积含水率也相应降低。降低速率与特征点高程呈正比。

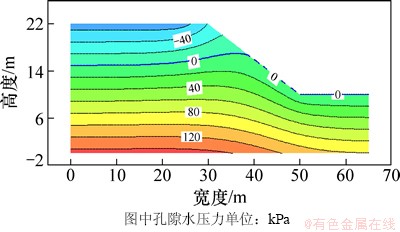
图7  降雨24 h后路堤边坡孔隙水压力分布

Fig. 7  Distribution of pore water pressure of embankment in 24 h after rainfall

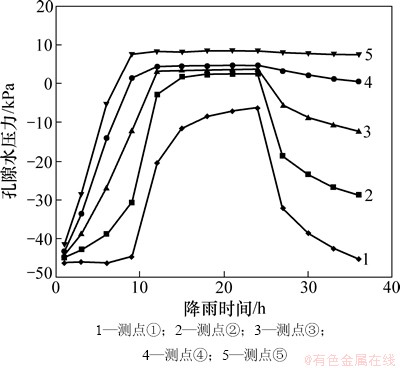
图8  降雨过程中特征点孔隙水压力变化

Fig. 8  Pore water pressure of feature points during rainfall

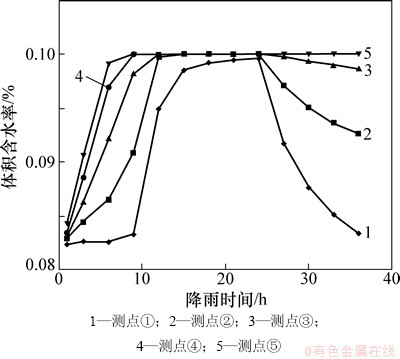
图9  降雨过程中特征点体积含水率变化

Fig. 9  Volumetric water content of feature points during rainfall

综上所述，路堤在降雨作用下表现为地下水位升高，路堤土体中基质吸力(负孔隙水)降低甚至消失，降雨入渗影响区域体积含水率增大或达到饱和含水率。以上物理量的变化可概括为以下几点：1) 地下水位的上升导致饱和区土体重度增大而引起下滑力增大；2) 非饱和区基质吸力降低或者变为正值，在一定程度上将降低其岩土体原有的抗剪强度；3) 对于高填方粗粒土路堤，雨水入渗导致路堤填料软化强度降低。基于以上几点，本文提出一种能够同时考虑上述因素的路堤边坡稳定性计算方法。

3.3  考虑降雨入渗与非饱和抗剪强度的路堤边坡稳定性计算及结果分析

3.3.1  三维模型的建立与计算参数

基于二维饱和-非饱和渗流有限元计算模型，建立平面等网格的FLAC-3D三维等效模型。其建立后的路堤横截面网格与二维有限元计算模型在形状、数量、大小上完全保持一致，并自编相关转换程序将二维饱和-非饱和渗流计算结果中各个时刻的孔隙水压力按节点导入三维模型中。孔隙水压力导入后的三维模型见图10(只列出了降雨24 h后的三维数值模型图)。对比图10和图7可知：由本文自编程序导入的孔隙水在其分布和大小上都与二维饱和-非饱和渗流计算结果一致。经过这种处理，有效地避免了FLAC-3D计算软件在自身渗流计算模块中将负孔隙水压力归“0”的弊端，在一定程度上提高了路堤稳定性计算结果的准确性。

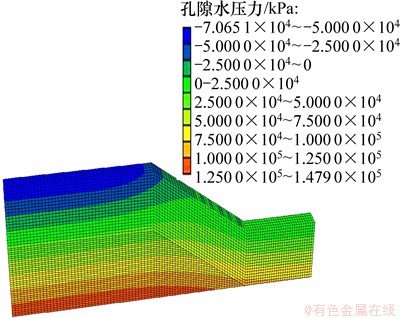
图10  导入孔隙水压力后的路堤三维模型图

Fig. 10  3D model diagram of embankment after importing pore water pressure

应力计算边界条件如下：铅直边界上施加水平约束，水平底部边界上施加铅直约束。本构模型为摩尔-库仑弹塑性本构模型，安全系数计算方法为强度折减法^[17]。

计算中所用黏聚力c按照式(10)中的(c′-u_wtan φ^b)进行设置，土体重度根据孔隙水压力在γ_d与γ_sat进行线性插值赋值。

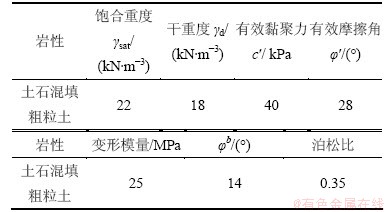
其余相关物理力学根据本文进行的室内试验与业主工地试验室提供参数综合取值，见表1。

表1  路堤边坡岩土体物理力学参数

Table 1  Physical & mechanical parameter of rock and soil of embankment slope

3.3.2  路堤边坡稳定性计算结果分析

降雨过程前降雨12 h和24 h的路堤边坡塑性区分布分别如图11~13所示。由图11~13可知：随着降雨的持续，路堤边坡塑性区面积逐渐增大，并沿着坡面向上延伸，其塑性区分布主要位于路堤边坡表层与地下水位线以下区域；在降雨开始前，边坡塑性区主要分布在边坡坡脚处，该位置塑性区出现主要是在路堤边坡岩土体自重作用下产生的；当降雨持续12 h和24 h时，边坡塑性区的发展则是边坡表层基质吸力丧失、岩土体重度增大、有效应力降低引起的。由此可见引起上诉塑性区发展变化规律的主要因素主要有：边坡表层处于边坡临空面，其自稳能力不强；由于地下水位上升引起地下水位以下土体有效应力减小，非饱和等效黏聚力(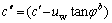)因为水压力的存在而降低，最终导致非饱和抗剪强度降低；此外，由于雨水入渗，边坡表层及地下水位以下区域岩土体重度增大，引起边坡坡面下滑力增大。

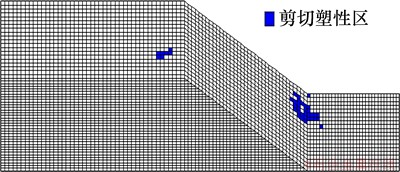
图11  降雨开始前路堤边坡塑性区分布图

Fig. 11  Distribution map of plastic zone of embankment slope before rainfall

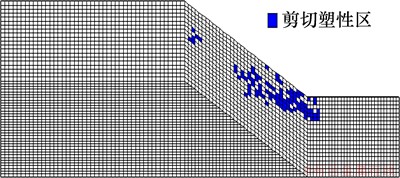
图12  降雨12 h路堤边坡塑性区分布图

Fig. 12  Distribution map of plastic zone of embankment slope within 12 h during rainfall

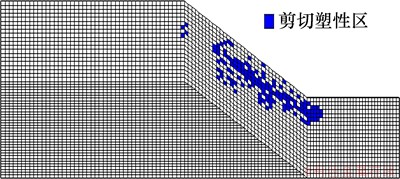
图13  降雨24 h堤边坡塑性区分布图

Fig. 13  Distribution map of plastic zone of embankment slope within 24 h during rainfall

3.3.3  路堤边坡瞬态安全系数变化分析

基于路堤边坡在降雨作用下塑性区发展变化规律，结合FLAC-3D强度折减法对路堤边坡在降雨过程及降雨停止一段时间后的安全系数进行计算，其变化规律如表2所示。由表2可知：路堤边坡在当降雨0~24 h时安全系数逐渐降低；当降雨持续24 h时，安全系数降低为1.28；当降雨停止后(降雨24 h)，路堤边坡安全系数有明显增大趋势，这表明降雨停止后雨水的出渗导致路堤内部基质吸力得到了一定恢复，岩土体重度降低。虽然算例中的路堤边坡在持续降雨过程中安全系数都高于规范所规定的最低值，但通过观察安全系数变化规律易知其安全系数在降雨持续时间延长的条件下有进一步下降的趋势，使路堤存在失稳的风险。因此，在降雨持续时间长、降雨量大的地区修建高填方路堤，其路堤边坡防排水措施的合理布置显得尤为重要。

表2  不同时刻粗粒土路堤边坡稳定性安全系数

Table 2  Safety factor of slope stability of granular soil embankment at different moments

4  结论

1) 降雨入渗导致路堤地下水位显著升高，但当升高到一定高度后，由于雨水出渗速度增大，地下水位升高速率存在减缓的趋势；降雨停止后，地下水位降低明显。

2) 边坡表层受降雨入渗影响区域孔隙水压力随着降雨的入渗由负值逐渐增大，甚至在饱和区变为正值；受降雨影响区域体积含水率逐渐增大，直到土体饱和时的饱和含水率；降雨停止后，孔隙水压力与体积含水率因雨水出渗而降低。

3) 降雨条件下路堤边坡塑性区主要分布在表层，塑性区随入渗影响区域的增大而增大，路堤安全系数也随之降低，降雨停止后安全系数逐渐恢复。

4) 本文提出的基于饱和-非饱和渗流及非饱和抗剪强度理论的路堤边坡稳定性分析方法既能真实反映路堤内基质吸力的变化，又能考虑由于降雨入渗引起的岩土体物理力学参数变化对路堤稳定性的影响。

参考文献：

[1] Ng C W, Shi Q. A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage[J]. Computers and Geotechanics, 1998, 22(1): 1-28.

[2] 孙广忠. 中国典型滑坡[M]. 北京: 科学出版社, 1998: 55-58.

SUN Guangzhong. China’s typical landslide[M]. Beijing: Science Press, 1998: 55-58.

[3] 邱文. 基质吸力对非饱和土边坡稳定性影响分析[J]. 安徽建筑工业学院学报, 2011, 19(6): 51-53.

QIU Wen. Influence of matric suction in unsaturated soils on slope stability[J]. Journal of Anhui Institute of Architecture & Industry, 2011, 19(6): 51-53.

[4] 邹维列, 李聪, 汪建峰, 等. 非饱和路堤对加载和降雨入渗响应的模型试验研究[J]. 岩土工程学报, 2009, 31(10): 1512-1519.

ZOU Weilie, LI Cong, WANG Jianfeng. Model tests on responses of unsaturated road-embankments to loading and rainfall infiltration[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1512-1519.

[5] 李佳, 高广运, 黄雪峰. 非饱和原状黄土边坡浸水试验研究[J]. 岩石力学与工程学报, 2011, 30(5): 1043-1048.

LI Jia, GAO Guangyun, HUANG Xuefeng. Experimental research on immersion for unsaturated intact loess slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5): 1043-1048.

[6] 牛文明, 高武振, 杨贺荣, 等. 饱和土与非饱和土固结理论及其联系与差别[J]. 科技信息, 2010, 3: 86-89.

NIU Wenming, GAO Wuzhen, YANG Herong, et al. Saturated soil and unsaturated soil consolidation theory and its relation and difference[J]. Technical Information, 2010, 3: 86-89.

[7] CHAO Yang, DAI Chaosheng, Carter J P. Effect of hydraulic hysteresis on seepage analysis for unsaturated soils[J]. Computers and Geotechnics, 2012, 41: 36-56.

[8] 王协群, 张有祥, 邹维列, 等. 降雨入渗条件下非饱和路堤变形与边坡的稳定数值分析[J]. 岩土力学, 2010, 31(11): 3640-3655.

WANG Xiequn, ZHANG Youxiang, ZOU Weilie, et al. Numerical simulation for unsaturated road-embankment deformation and slope stability under rainfall infiltration[J]. Rock and Soil Mechanics, 2010, 31(11): 3640-3655.

[9] 沈水进, 孙红月, 尚岳全, 等. 降雨作用下路堤边坡的冲刷-渗透耦合分析[J]. 岩石力学与工程学报, 2011, 30(12): 2456-2462.

SHEN Shuijin, SUN Hongyue, SHANG Yuequan, et al. Scouring-penetration coupling analysis of embankment slope under rainfall action[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(12): 2456-2462.

[10] 陈晓斌, 徐望国, 刘小平. 降雨入渗对粗粒土路堤变形与稳定性的影响[J]. 中南大学学报(自然科学版), 2011, 42(3): 765-771.

CHEN Xiaobin, XU Wangguo, LIU Xiaoping. Effect of rainfall infiltration on additional settlement and stability debasement of granular soil fillings embankment[J]. Journal of Central South University (Science and Technology), 2011, 42(3): 765-771.

[11] 蒋中明, 曾铃, 付宏渊, 等. 降雨条件下厚覆盖层边坡的渗流特性[J]. 中南大学学报(自然科学版), 2012, 43(7): 2782-2788.

JIANG Zhongming, ZENG Ling, FU Hongyuan, et al. Seepage characteristics of thick coating slope in raining condition[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2782-2788.

[12] 孔祥言. 高等渗流力学[M]. 合肥: 中国科学技术大学出版社, 2010: 77-79.

KONG Xiangyan. Higher seepage mechanics[M]. Hefei: China Science and Technology University Press, 2010: 77-79.

[13] 付宏渊, 曾铃, 蒋中明, 等. 降雨条件下公路边坡暂态饱和区发展规律[J]. 中国公路学报, 2012, 25(3): 59-64.

FU Hongyuan, ZENG Ling, JIANG Zhongming, et al. Developing law of transient saturated areas of highway slope under rainfall conditions[J]. China Journal of Highway and Transport, 2012, 25(3): 59-64.

[14] van Genuchten M T. A closed form equation for prediction the hydraulic conductivity of unsaturated soils[J]. Soil Sci Soc Am J, 1980, 44: 892-898.

[15] Mohr O. Welcle umstande bedingen die elastizitatsgrenze und den bruch eines materials[J]. Zeitschrift des Vereins Deutscher Ingenieure, 1900, 44: 1524-1530.

[16] Ho D Y F, Fredlund D G. A multi-stage triaxial test for unsaturated soil[J]. ASTM Geotechnical Testing Journal, 1982, 5(1/2): 18-25.

[17] Matsui T, San K C. Finite element slope stability analysis by shear strength reduction technique[J]. Soil and Foundations, JSSMFE, 1992, 32(1): 59-70.

(编辑  陈灿华)

收稿日期：2013-03-01；修回日期：2014-05-18

基金项目(Foundation item)：国家自然科学基金资助项目(51078042，51278067)；长沙理工大学道路结构与材料交通行业重点实验室开放基金资助项目(kfj110206)；湖南省科学技术厅科技计划重点项目(2013FJ2008)；湖南省交通运输厅科技计划项目(2009003)(Projects (51078042，51278067) supported by National Natural Science Foundation of China; Project (kfj110206) supported by Open Fund of Key Laboratory of Road Structure and Material of Ministry of Transport, Changsha University of Science & Technology; Project (2013FJ2008) supported by Science and Technology Plan Key Project of Hunan Provincial Science and Technology Department; Project (2009003) supported by Science and Technology Plan Project of Hunan Provincial Trans)

通信作者：曾铃(1986-)，男，重庆江津人，博士研究生，从事岩土工程和道路工程的研究；电话：13975853510；E-mail：zlbingqing3@126.com