DOI: 10.11817/j.issn.1672-7207.2017.08.016
基于支撑集估计的压缩扩频接收机
郭黎利,刘湘蒲,孙志国
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨,150001)
摘要:为了提升压缩扩频接收机的误码率性能,提出一种基于支撑集估计的改进压缩扩频接收机。改进的接收机首先估计稀疏信号的支撑集,然后通过求解闭合表达式代替原有的重构算法来获取发送的信息序列,从而达到降低系统误码率的目的。将改进的压缩扩频接收机应用于mW复合序列扩频信号的接收,通过检测mW复合序列的循环谱峰值来估计稀疏信号的支撑集。研究结果表明:对于mW复合序列,在低信噪比下,通过循环谱检测能有效实现支撑集的估计,且改进的压缩扩频接收机比现有的压缩扩频接收机具有更好的误码率性能。
关键词:压缩感知;扩频接收机;支撑集估计;mW复合序列;循环谱
中图分类号:TN914.42 文献标志码:A 文章编号:1672-7207(2017)08-2088-09
Compressive spread spectrum receiver based on support estimation
GUO Lili, LIU Xiangpu, SUN Zhiguo
(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
Abstract: In order to improve the bit-error-rate (BER) performance of compressive spread spectrum (CSS) receiver, a modified CSS receiver based on support estimation was proposed. In the modified receiver, support of sparse signal was estimated firstly, and then the transmitted information sequence can be achieved by solving a closed-form expression instead of the original reconstructed algorithm, which can reduce the BER of receiver. The modified CSS receiver was used to receive m-Walsh (mW) composite sequence spread spectrum signal, and the support of sparse signal can be estimated by detecting cyclic spectrum peak of mW composite sequence. The results show that for mW composite sequence, the support of sparse signal can be estimated effectively in low signal-to-noise ratio (SNR), and the modified CSS receiver has a better BER performance than CSS receiver.
Key words: compressive sensing; spread spectrum receiver; support estimation; m-Walsh composite sequence; cyclic spectrum
压缩感知(简称CS)是由DONOHO等[1-7]提出的一种新的信号处理理论。在该理论框架下,通过利用信号的稀疏性,并采用随机采样结构(如RD[8]和MWC[9]等)能有效降低信号处理所需的采样率。近年来,压缩感知理论开始在扩频通信领域得到应用。AGGARWAL等[10]利用二阶Reed-Muller码构建压缩测量矩阵,并将CS应用于扩频通信系统,降低了多用户检测时的复杂度,但其实现仅适用于通过二阶Reed-Muller码构建的测量矩阵。LI等[11]将CS应用于GPS接收机,减少了接收机中相关器的数目,降低了复杂度和功耗。FYHN等[12]将CS应用于直接序列扩频通信(DSSS)中,通过改进接收机中匹配滤波器的结构来实现信号的压缩测量,降低了采样率,但增加了匹配滤波器的复杂度。FYHN等[13]指出在DSSS系统中,发送的扩频序列需从扩频序列集中进行选取,由此表现出一定的稀疏性。利用此稀疏性,该文提出了压缩扩频(CSS)的概念,并构建了压缩扩频接收机(CSS Receiver)。与传统的扩频接收机相比,压缩扩频接收机的结构极其简单,能够有效降低功耗和硬件成本。在压缩扩频接收机中,首先对接收信号进行压缩测量,然后采用重构算法从压缩测量值中恢复出发送的信息序列。而在CS理论中,通过重构算法对于原始信号的恢复具有一定的概率,因此,对于压缩扩频接收机,其误码率性能较传统扩频接收机有所降低。基于CS理论,当稀疏信号支撑集已知时,可通过直接求解闭合表达式来获得原始信号的唯一解,故通过该方法恢复原始信号的概率将高于重构算法。因此,为了提升压缩扩频接收机的误码率性能,本文作者提出先估计稀疏信号支撑集,再通过获取的支撑集来恢复发送信息序列的改进思路,并构建了基于支撑集估计的压缩扩频接收机。在现有的扩频序列中,m-Walsh(mW)复合序列频谱峰值的位置与序列本身具有明确的对应关系,利用该特性,将压缩扩频接收机应用于mW复合序列扩频信号的接收,可估计出所需的支撑集。为了在低信噪比下实现支撑集的估计,在mW复合序列频谱特征的基础上,分析mW复合序列的循环谱特征,给出了通过循环谱检测来估计支撑集的算法流程。虽然本文作者将改进的压缩扩频接收机应用于mW复合序列的接收,但对于任何可以获取稀疏信号支撑集的扩频序列,改进的压缩扩频接收机仍然适用。
1 压缩扩频
为了简化,假定发射机和接收机之间已实现系统同步,并针对基带系统进行分析。
1.1 扩频发射机
图1所示为扩频发射机结构及其等效的向量表示形式。
发送的扩频信号可表示为
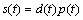 (1)
(1)
式中:
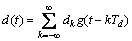
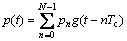 (2)
(2)
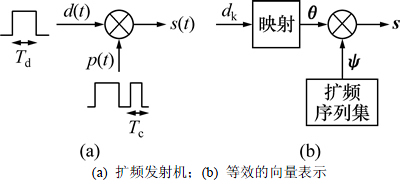
图1 扩频发射机及其等效的向量表示
Fig. 1 Diagram of spread spectrum transmitter and equivalent vector representation
g(t)为门函数;dk为发送的信息序列,根据不同的调制方式,dk选取不同的发送符号,如BPSK调制时,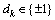 ,QPSK调制时,
,QPSK调制时,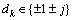 ;p(t)为扩频序列,从扩频序列集中选取;Td为符号持续时间;Tc为扩频序列切普持续时间,且Td=NTc。
;p(t)为扩频序列,从扩频序列集中选取;Td为符号持续时间;Tc为扩频序列切普持续时间,且Td=NTc。
对于扩频发射机,可通过等效的向量形式来表示发送的扩频信号
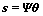 (3)
(3)
式中: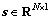 为s(t)的向量形式;
为s(t)的向量形式;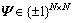 为扩频序列集,
为扩频序列集,
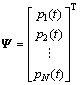 (4)
(4)
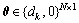 通过dk映射得到,用于选取扩频序列p(t),并包含了发送的信息序列dk。以BPSK调制为例,若发送的符号为-1,且扩频序列选取p2(t),则
通过dk映射得到,用于选取扩频序列p(t),并包含了发送的信息序列dk。以BPSK调制为例,若发送的符号为-1,且扩频序列选取p2(t),则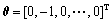 。
。
1.2 压缩扩频接收机
图2所示为现有压缩扩频接收机结构示意图。
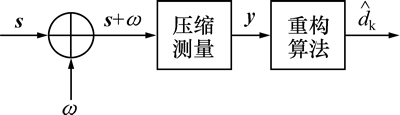
图2 压缩扩频接收机结构示意图
Fig. 2 Diagram of compressive spread spectrum receiver
由图2可以看出:对于直扩信号,向量θ只在序列集Ψ中选取一条扩频序列来进行传输,而θ中用于选取该序列的元素取值为dk,其余元素取值均为零,因此,θ为一稀疏向量。利用该稀疏性,可对信号进行压缩接收,接收过程为
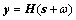 (5)
(5)
式中: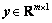 为压缩测量值,
为压缩测量值, 为压缩测量矩阵,且m<N,m/N为压缩率,记为κ;
为压缩测量矩阵,且m<N,m/N为压缩率,记为κ;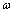 为高斯白噪声。
为高斯白噪声。
采用随机解调(简称RD)压缩采样结构来实现信号的压缩接收,则H中的元素由{0,1}组成。对于H中的第i(i=0,1,…,m-1)行,元素1分布在[iN/m+1,(i+1)N/m]的连续范围内。如m=3,N=6时,H为
 (6)
(6)
压缩扩频接收机的结构非常简单,仅需构造压缩测量矩阵H即可。
1.3 改进的压缩扩频接收机
为了方便表述,首先定义θ的支撑集S为θ中非零元素所在位置的下标集合,即
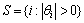 (7)
(7)
扩频信号从发射到接收的整个压缩测量过程可写为
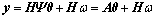 (8)
(8)
式中: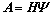 。
。
当m<N时,对于式(8)的求解是欠采样下的信号重构问题。基于θ的稀疏性,可以通过寻找满足等式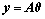 的最稀疏信号
的最稀疏信号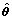 来恢复θ,即为求解如下最优化问题:
来恢复θ,即为求解如下最优化问题:
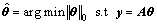 (9)
(9)
在压缩扩频接收机中,θ的支撑集未知,因此采用基于CS理论的重构算法来求解式(9),得到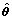 ,但在CS理论中,重构算法对于θ的恢复具有一定的概率,从而会造成系统误码率性能降低。
,但在CS理论中,重构算法对于θ的恢复具有一定的概率,从而会造成系统误码率性能降低。
但是,当稀疏向量θ的支撑集已知时,若A的子矩阵AS(AS由以S为索引的A中的列向量组成)为列满秩阵时,可通过如下所示的闭合表达式获得θ的唯一解:
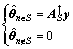 (10)
(10)
式中:n=1,2,…,N;S为θ的支撑集;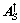 为AS的伪逆;
为AS的伪逆;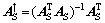 。
。
若子矩阵AS为秩亏阵,可加入1个正则项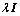 使得
使得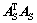 可逆,则θ的解改写为
可逆,则θ的解改写为
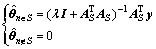 (11)
(11)
式中:λ>0,I为单位阵。
因此,若能在恢复θ之前先估计θ的支撑集,再通过闭合表达式直接获得θ的唯一解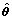 ,则比通过重构算法恢复的
,则比通过重构算法恢复的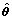 具有更高的正确率,从而可以提升系统的误码率性能。根据该思路,提出如图3所示的改进压缩扩频接收机。
具有更高的正确率,从而可以提升系统的误码率性能。根据该思路,提出如图3所示的改进压缩扩频接收机。
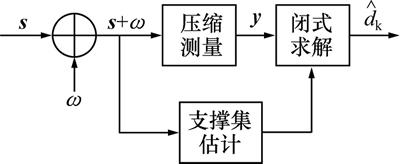
图3 改进的压缩扩频接收机结构示意图
Fig. 3 Diagram of modified compressive spread spectrum receiver
2 可用于支撑集估计的mW复合序列特征
mW复合序列的频谱和循环谱特征均可用于θ的支撑集估计。在低信噪比下,循环谱特征可获得更好的估计效果,但mW复合序列的循环谱与其频谱有关,因此,同时分析其频谱和循环谱。
2.1 mW复合序列频谱特征
以Walsh序列为基本序列,并根据m序列每个切普的符号来确定Walsh序列的极性,最后将这些基本序列串接可形成mW复合序列:
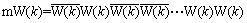 (12)
(12)
式中:W(k)表示序号为k的Walsh序列;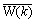 表示Walsh序列按位取反。
表示Walsh序列按位取反。
图4所示为m序列、Walsh序列和mW复合序列的频谱示意图。设m序列长度为M,切普速率为fm,Walsh序列长度为w,切普速率为fw,则mW复合序列的切普速率为fmW=fW,长度为N=Mw。
由图4可以看出:mW复合序列的频谱是由m序列的频谱沿频率轴缩短W倍后,与Walsh序列频谱卷积形成,即将m序列频谱各谱线间隔乘以1/w后,整体搬移到Walsh序列的各谱线位置,幅值由Walsh序列谱线决定[14-16]。
由Hadamard矩阵形成的Walsh序列的频谱中心频率fc(频谱峰值所对应的频率)与序列的序号k具有明确的对应关系,如表1所示。
表1 序号与中心频率对应关系
Table 1 Relationship between k and fc


图4 m序列、Walsh序列和mW复合序列频谱示意图
Fig. 4 Spectrum of m sequence, Walsh sequence and mW composite sequence
W(0)为直流信号,W(1)的中心频率为fw/2。从W(2)到W(w-1)的序列对应了(w-2)/2种不同的中心频率,其中序号为
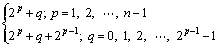 (13)
(13)
的2个序列具有相同的中心频率。
序号从2p到2p+1-1的Walsh序列的中心频率与系数λ有关,而系数λ可通过图5所示方法得到。
系数λ的求取为一个循环过程。如图5所示为第l次循环(l初始值取0)。每次循环从状态j=0开始,直到状态j=7结束。图中每个状态的取值即为系数λ的值,其中符号L设定为L=2p-2-1。随着状态的变化,与λ对应的q为q=8l+j。如此循环,直到获得所有的λ和对应的q。
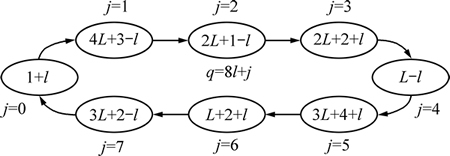
图5 系数λ的求取过程
Fig. 5 Calculation of parameter λ
设w=8,以W(7)为例,求取其中心频率fc。此时,7=22+1+21,则p=2,q=1。对应图5,可得l=0,j=1,则λ=3,再由表(1)可知W(7)的中心频率fc=3fw/8。同时由式(13)可知,W(7)与W(22+1),即W(5)具有相同的fc。依此类推,可得W(2)与W(3)具有相同的fc=fw/4,W(4)与W(6)具有相同的fc=fw/8。
2.2 mW复合序列循环谱特征
mW复合序列扩频信号与一般扩频信号相同,同样具有循环平稳特性,而噪声和干扰一般为平稳过程,不具备循环平稳特性。因此,利用信号的循环谱,能够在低信噪比下对信号参数进行估计。
为了分析,将基于mW复合序列的扩频信号s(t)写为
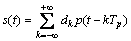 (14)
(14)
式中:p(t)为mW复合序列;Tp为复合序列周期。
s(t)与数字脉冲幅度调制(简称为PAM)信号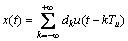 具有类似的表达式。PAM信号的循环谱表达式为[17-18]
具有类似的表达式。PAM信号的循环谱表达式为[17-18]
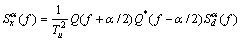 (15)
(15)
式中:α为循环频率;f为频率;Q(f)为脉冲u(t)的频谱;Q*(f)为Q(f)的共轭;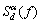 为
为
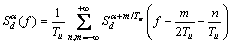 (16)
(16)
若dk为平稳随机过程,有
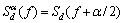 (17)
(17)
则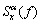 可改写为
可改写为
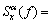
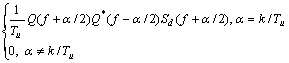 (18)
(18)
式中:Sd(f)为序列dk的功率谱。
假设dk是独立同分布的,则Sd(f)为常数。由此,可得到s(t)的循环谱表达式为
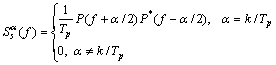 (19)
(19)
式中:P(f)为mW复合序列频谱,故s(t)的循环谱特征由mW复合序列频谱决定。
mW复合序列的频谱P(f)由缩短的m序列频谱与Walsh序列频谱卷积形成。m序列频谱峰值出现在零频附近,Walsh序列频谱峰值出现在中心频率fc,故P(f)的峰值位置将出现在中心频率fc附近。因此,对于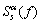 ,当f=0时,循环谱切面
,当f=0时,循环谱切面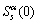 的峰值将出现在
的峰值将出现在 附近。
附近。
故通过检测s(t)循环谱切面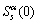 的峰值可估计出参数fc,再通过fc与Walsh序列序号的对应关系,可将s(t)的可能性限制在最多2条mW复合序列范围内,由此可获得θ的估计支撑集。
的峰值可估计出参数fc,再通过fc与Walsh序列序号的对应关系,可将s(t)的可能性限制在最多2条mW复合序列范围内,由此可获得θ的估计支撑集。
3 支撑集估计
将长度为7的m序列与长度为8的Walsh序列进行复合得到mW复合序列。图6所示为当频率f=0 Hz时,mW(0)~mW(7)的循环谱切面图。图中设定fw=1 Hz,采样率fs=4 Hz。以mW(5)和mW(7)为例,由于W(5)和W(7)具有相同的中心频率fc=3fw/8,故mW(5)和mW(7)的循环谱切面峰值均出现在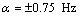 附近。其余复合序列的循环谱切面峰值依此类推。
附近。其余复合序列的循环谱切面峰值依此类推。
由于W(0)为直流信号,故mW(0)实际为串接的m序列。因此,支撑集的估计只针对序号k>0的复合序列。具体的估计算法流程如图7所示。
1) 为了降低噪声的影响,将接收到的数据分为T段,每段长度为L。
2) 对第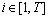 段数据求取其循环谱,并获得f=0的切面
段数据求取其循环谱,并获得f=0的切面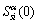 ,最后将得到的T个切面进行累加平均来降低噪声影响,得到平均后的切面
,最后将得到的T个切面进行累加平均来降低噪声影响,得到平均后的切面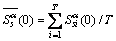 。
。
3) 在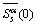 循环频率轴上搜索最大的2个峰值,标记为p1和p2,得到两峰值的间距
循环频率轴上搜索最大的2个峰值,标记为p1和p2,得到两峰值的间距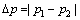 ,并根据循环频率分辨率
,并根据循环频率分辨率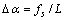 得到估计的中心频率
得到估计的中心频率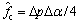 。
。
4) 根据fc与Walsh序列序号的对应关系,通过估计的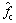 可得到θ的估计支撑集。
可得到θ的估计支撑集。
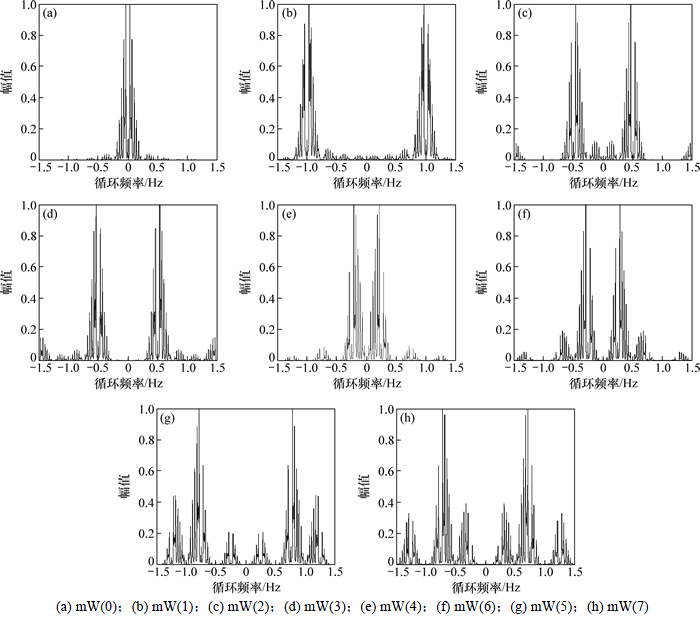
图6 循环谱切面图(f=0)
Fig. 6 Cyclic spectrum at f=0
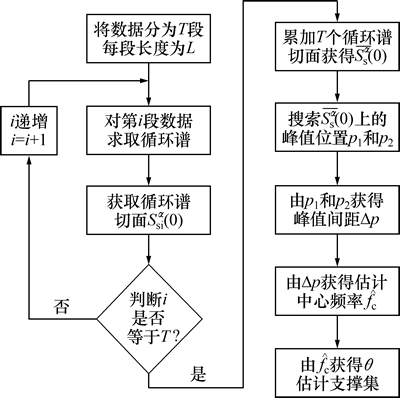
图7 支撑集估计算法流程
Fig. 7 Algorithm flow chart of support estimation
4 实验仿真与分析
利用mW复合序列频谱主瓣位置可控的特征,针对认知无线电(简称CR)中的直扩认知用户,可将mW复合序列作为直扩认知用户的扩频序列,使其发射信号频谱在授权用户工作频段内凹陷,从而实现直扩认知用户的频谱接入[21],接入示意图如图8所示。
基于mW复合序列的直扩认知用户在进行频谱接入时,可通过码位移[22-23]技术增加可用复合序列的数目。使用不同初始相位的m序列来区分不同的接入频段,而在同一接入频段内采用不同的Walsh序列来改变频谱凹陷宽度。此时,认知用户接入的频段被划分为M段,分别为[B1,B2,…,BM]。在第Bi频段中,接入的复合序列miW(k)由位移i个切普的m序列与Walsh序列复合形成。
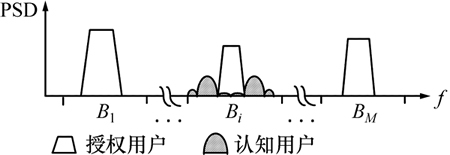
图8 mW复合序列直扩认知用户频谱接入示意图
Fig. 8 Spectrum access of mW composite sequence direct sequence spread spectrum secondary user
在仿真实验中,构建该频谱接入方式,并分别采用现有压缩扩频(CSS)接收机和改进的压缩扩频(改进CSS)接收机对发射信号进行接收,比较接收机的误码率性能。
m序列长度为7,Walsh序列由8阶Hadamard矩阵生成。8条Walsh序列分别与移位的m序列复合形成包含56条mW复合序列的扩频序列集。发射信号采用BPSK调制方式,则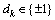 。所加噪声为高斯白噪声ω。信噪比rSNR定义为
。所加噪声为高斯白噪声ω。信噪比rSNR定义为
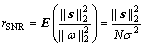 (20)
(20)
式中: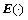 为求均值;
为求均值;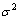 为噪声方差。
为噪声方差。
4.1 支撑集估计性能分析
在系统同步条件下,发射信号的载频已知,由此可获得mW复合序列频谱接入的频段Bi及对应的移位m序列。因此,仅需估计Walsh序列的序号即可获得θ的估计支撑集。
向量θ中非零元素的位置在[1:56]之间随机选取,概率服从均匀分布。dk为随机生成的+1或者-1。由于W(2)/W(3),W(4)/W(6)及W(5)/W(7)分别具有相同的中心频率fc,因此支撑集估计正确的衡量标准为所估计的支撑集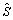 中包含了真实的支撑集S。设定fw=1 Hz,采样率fs=4 Hz。信号循环谱通过频率平滑循环周期图法得到,每次计算循环谱的数据长度为L,且切面
中包含了真实的支撑集S。设定fw=1 Hz,采样率fs=4 Hz。信号循环谱通过频率平滑循环周期图法得到,每次计算循环谱的数据长度为L,且切面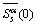 由10次计算的
由10次计算的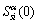 切面累加平均得到。
切面累加平均得到。
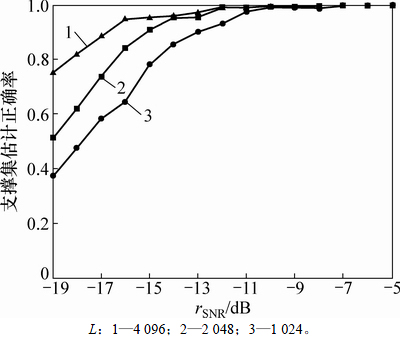
图9 支撑集估计正确率
Fig. 9 Correct rate of support estimation
图9所示为不同信噪比下,L取不同值,估计500次所得到的支撑集估计正确率。从图9可知:随着L的增加,估计正确率得到提升。若要估计正确率达到90%以上,数据长度L=1 024时所需信噪比为-13 dB,L=2 048时所需信噪比为-15 dB,L=4 096时所需信噪比为-16 dB。
4.2 系统误码率分析
下面分析系统的误码率(简称BER)。发送信息序列dk获取正确的判定标准包含了2个方面:1) θ中非零元素的位置正确;2) dk的极性正确。但从图9可以看出:在信噪比较低时,可能出现错误的支撑集估计,从而导致获取的dk均被判定为误码,这也是本文改进方法的不足之处。为了避免该问题,在进行误码率分析时,假定支撑集的估计完全正确。
在现有CSS中,对于θ的重构采用与文献[9]相同的子空间追踪(简称SP)算法[24-25],SP算法具有较好的重构效果,且计算复杂度较低。对于改进的CSS,基于m序列良好的自相关性和Walsh序列良好的互相关性,子矩阵AS易满足列满秩条件,因此,直接通过式(10)获取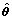 。
。
图10所示为不同移位m序列与同一Walsh序列形成的复合序列的接收性能。固定Walsh序列为W(7),压缩率κ=0.75。从图10可以看出:不同移位m序列构成的mW复合序列具有基本相同的误码率曲线,因此移位的m序列并不对系统的误码率产生影响。比较CSS和改进CSS,可以看出,在信噪比较低时,改进CSS的误码率明显低于现有的CSS。随着信噪比的增加,现有CSS的误码率曲线下降速度快于改进CSS,但其误码率仍然高于改进CSS。这是由于随着信噪比的增加,SP算法的重构概率增加,当信噪比达到一定值时,SP算法可以高概率重构出θ。
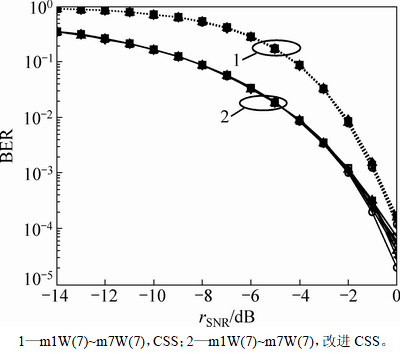
图10 不同m序列下,CSS与改进CSS系统误码率
Fig. 10 BER of compressive spread spectrum and modified compressive spread spectrum with different m sequences
图11所示为不同序号Walsh序列与同一m序列形成的复合序列的接收性能。m序列选取m1,压缩率κ=0.75。

图11 不同Walsh序列下,CSS与改进CSS系统误码率
Fig. 11 BER of compressive spread spectrum and modified compressive spread spectrum with different Walsh sequences
由图11可知:对于CSS,不同Walsh序列对应的mW复合序列具有几乎相同的误码率曲线,因此不同的Walsh序列并不影响系统的误码率。对于改进CSS,m1W(1)的误码率明显低于其他的复合序列的误码率。这是由于在进行支撑集估计时,m1W(1)对应的估计支撑集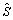 仅包含1个支撑,而其余的复合序列包含了2个可能的支撑,而在通过式(10)获取
仅包含1个支撑,而其余的复合序列包含了2个可能的支撑,而在通过式(10)获取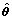 时,更准确的估计支撑集将使得获取的
时,更准确的估计支撑集将使得获取的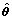 更准确。
更准确。
图12所示为在不同压缩率κ下,改进CSS的误码率曲线。图12所示的误码率曲线为m1W(1)~m1W(7)的误码率平均值。当压缩率κ=1.0时,压缩测量矩阵H取单位阵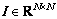 ,表示不对信号进行压缩。
,表示不对信号进行压缩。
在图12中,随着压缩率的增加,系统的误码率性能得到改善。当压缩率大于0.6后,改进CSS能够较好的获得发送的信息序列。在误码率为10-4,压缩率为0.8时,改进CSS要达到与压缩率为1时相同的误码率,所需的信噪比需增加1 dB左右,压缩率为0.6时,需增加2 dB左右。
图13所示为改进CSS与现有CSS在不同压缩率下的误码率性能比较。图13中的误码率曲线为m1W(1)~m1W(7)的误码率平均值。压缩率分别取κ=0.6和κ=0.8,在误码率为10-4时,改进CSS比现有CSS所需的信噪比降低了2 dB左右。
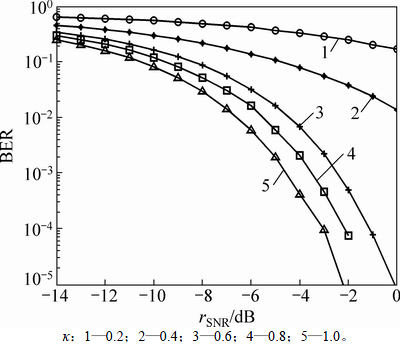
图12 不同压缩率下,改进CSS系统误码率
Fig. 12 BER of modified compressive spread spectrum with different compressed ratios

图13 不同压缩率下,CSS与改进CSS系统误码率
Fig. 13 BER of compressive spread spectrum and modified compressive spread spectrum with different compressed ratios
5 结论
1) 针对压缩扩频接收机,提出先估计稀疏信号支撑集,再通过闭合表达式代替重构算法来获取发送信息序列的改进方法,构建基于支撑集估计的压缩扩频接收机。
2) 将改进的压缩扩频接收机应用于mW复合序列的接收,利用mW复合序列的循环谱特征实现支撑集估计,降低系统误码率。虽然本文以mW复合序列为例进行接收,但改进的接收机适用于任何可获得稀疏信号支撑集的扩频序列。
3) 当信噪比较低时,会出现支撑集的估计错误,从而导致误码率性能急剧下降,这是改进方法的不足之处,但通过增加数据长度可以改善支撑集的估计效果。
参考文献:
[1] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[2] CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[3] CANDES E. Compressive sampling[C]//Proceedings of International Congress of Mathematicians. Madrid, Spain, 2006: 1433-1452.
[4] DONOHO D L. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 533-548.
[5] BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121.
[6] CANDES E, ROMBERG J, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.
[7] 焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651-1662.
JIAO Licheng, YANG Shuyuan, LIU Fang, et al. Development and prospect of compressive sensing[J]. Acta Electronica Sinica, 2011, 39(7): 1651-1662.
[8] KIROLOS S, LASKA J, WAKIN M, et al. Analog-to-information conversion via random demodulation[C]// Proceedings of 2006 IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software. Dallas, USA: IEEE, 2006: 71-74.
[9] MISHALI M, ELDAR Y C. From theory to practice: sub-Nyquist sampling of sparse wideband analog signals[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 375-391.
[10] AGGARWAL V, APPLEBAUM L, BENNATAN A, et al. Enhanced CDMA communications using compressed sensing reconstruction methods[C]//Proceedings of 47th Annual Allerton Conference on Communication, Control, and Computing. Monticello, USA: IEEE, 2009: 1211-1215.
[11] LI X, RUEETSCHI A, ELDAR Y C, et al. GPS signal acquisition via compressive multichannel sampling[J]. Physical Communication, 2012, 5(2): 173-184.
[12] FYHN K, ARILDSEN T, LARSEN T, et al. Demodulating subsampled direct sequence spread spectrum signals using compressive signal processing[C]//Proceedings of the 20th European Signal Processing Conference (EUSIPCO). Bucharest, Romanian: IEEE, 2012: 2556-2560.
[13] FYHN K, JENSEN T L, LARSEN T, et al. Compressive sensing for spread spectrum receiver[J]. IEEE Transactions on Wireless Communications, 2013, 12(5): 2334-2343.
[14] 郭黎利. 具有DS/FH频谱特性的复合序列扩频通信方式[J]. 哈尔滨工程大学学报, 1998, 19(4): 24-30.
GUO Lili. Communication mode of composite sequence spread spectrum with DS/FH spectrum feature[J]. Journal of Harbin Engineering University, 1998, 19(4): 24-30.
[15] 郭黎利, 付江志, 崔永生, 等. 采用m-W复合序列的直扩系统规避窄带干扰的研究[J]. 哈尔滨工程大学学报, 2010, 31(5): 646-651.
GUO Lili, FU Jiangzhi, CUI Yongsheng, et al. Using m-Walsh composite sequences to reduce narrow-band interference in direct sequence spread spectrum system[J]. Journal of Harbin Engineering University, 2010, 31(5): 646-651.
[16] 付江志, 郭黎利, 杨红乔. 基于复合序列的多进制正交扩频系统性能分析[J].系统工程与电子技术, 2010, 32(4): 222-225.
FU Jiangzhi, GUO Lili, YANG Hongqiao. Performances of M-ary orthogonal code spread spectrum system based on composite sequence[J]. Systems Engineering and Electronics, 2010, 32(4): 222-225.
[17] GARDNER W A. Spectral correlation of modulated signals: part I-analog modulation[J]. IEEE Transactions on Communications, 1987, 35(6): 584-594.
[18] 张天骐, 何丹娜, 陈适, 等. 基于谱相关的BOC调制信号参数估计[J]. 华中科技大学学报(自然科学版), 2013, 41(9): 11-16.
ZHANG Tianqi, HE Danna, CHEN Shi, et al. Spectral correlation-based parameter estimation of BOC modulation signal[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(9): 11-16.
[19] Mitola J. Cognitive radio for flexible mobile multimedia communications[C]//Proceedings of IEEE Sixth International Workshop on Mobile Multimedia Communications (MoMuC’99). San Diego, CA, IEEE, 1999: 3-10.
[20] Mitola J, Maguire G Q. Cognitive radio: making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-18.
[21] 郭黎利, 刘湘蒲, 付江志, 等. 基于块编码的功率谱可控复合序列[J]. 哈尔滨工程大学学报, 2015, 36(2): 248-251.
GUO Lili, LIU Xiangpu, FU Jiangzhi, et al. Controllable composite sequence of power spectral density based on the block coded signal[J]. Journal of Harbin Engineering University, 2015, 36(2): 248-251.
[22] 王辉, 郭黎利. 基于码位移的复合序列扩频通信认知无线电信道兼容技术[J]. 自动化技术与应用, 2013, 32(4): 32-35.
WANG Hui, GUO Lili. A technology of channel coexistence in cognitive radio based on spread spectrum-composite sequence-code shift keying[J]. Techniques of Automation and Applications, 2013, 32(4): 32-35.
[23] YUH-REN T. M-ary spreading code phase shift keying modulation for DSSS multiple access systems[J]. IEEE Transactions on Communications, 2009, 57(11): 3220-3224.
[24] WEI D, MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249.
[25] Varadarajan B, Khudanpur S, Tran T D. Stepwise optimal subspace pursuit for improving sparse recovery[J]. IEEE Signal Processing Letters, 2011, 18(1): 27-30.
(编辑 陈爱华)
收稿日期:2016-09-08;修回日期:2016-12-24
基金项目(Foundation item):国家自然科学基金资助项目(61271263)(Project (61271263) supported by the National Natural Science Foundation of China)
通信作者:郭黎利,博士,教授,从事现代通信系统理论与技术、通信信号处理技术研究;E-mail:guolili@hrbeu.edu.cn