基于量子连续变量EPR态的经典消息匿名通信方案
娄小平1, 2,陈志刚2,邓小鸿2,李贤2,梅晓勇1
(1. 湖南文理学院 计算机科学与技术学院,湖南 常德,415000;
2. 中南大学 信息科学与工程学院,湖南 长沙,410083)
摘要:针对目前已提出的量子匿名通信协议都只建立在参与者是非自适应的基础上,而实际操作过程中参与者的自适应性是不可忽略的因素,合并信息传输和信道检测这2个过程到同一次编码中,对多方安全计算的匿名通信模型进行优化。方案使用N+1对量子连续变量EPR态,采用移动式量子态传输,将N bit经典消息编码在不同的模式中,消息接收者通过计算得到匿名消息并检验当次通信中参与者的诚实度,使得通信方案的效率提高。研究结果表明:除了指数小的概率外,发送者和接收者的匿名性和消息的私密性都得到保护。
关键词:匿名通信;量子纠缠;私密性;EPR态
中图分类号:TP309 文献标志码:A 文章编号:1672-7207(2014)09-3043-06
Anonymous transmissions scheme of classical information based on quantum continuous variable entanglement states
LOU Xiaoping1, 2, CHEN Zhigang2, DENG Xiaohong2, LI Xian2, MEI Xiaoyong1
(1. School of Computer Science and Technology, Hunan University of Arts and Science, Changde 415000, China;
2. School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Quantum anonymous communication schemes were proposed on the condition that the participants are non-adaptive, but adaptability of participants can not be ignored in the actual operation, and so the multiple secure computing model for anonymous communication was optimized which incorporated message transmission and channel detection together in the process of encoding. N +1 EPR states’s continuous variable quantum encoded in different modes travelled among the participants, and receiver of the message could get the results by calculating and the results could be verified when the participant was dishonesty. The results show that efficiency of the scheme is effective. Furthermore, the anonymity of sender and receiver and privacy of messages are protected except with exponentially small probability.
Key words: anonymous communication; quantum entanglement; privacy; EPR state
在大多数加密算法应用中,人们研究的兴趣集中于保护传输消息的私密性。消息的发送者和接收者都知道对方的身份,他们尽量使对方无法窃取传输消息。然而,匿名性是对身份的保密,在密码学应用中,匿名消息传输旨在保护消息发送者或接收者的身份,该特性使得成员即使是传输的消息公开的情况下也可以匿名地发送消息或接收消息。在匿名访问、电子商务、选举投票和匿名邮件等领域都广泛应用了匿名消息传输技术。1988年Chaum[1]提出了密码学家就餐问题,3个密码学家两两秘密掷币,通过计算参与者输入数据的奇偶性匿名广播经典消息。这是最初的经典匿名通信模型。在随后的研究中,一般将此模型称为DC-net。在现有技术应用的实际操作中,通常引入可信的第三方[2]来充当信息中继站,中继转发过程掩蔽身份。最早Webmixes和ISDN[3]作为中继转发技术广泛运用到通信中。紧接着,Mixmaster匿名通信模型[4]、PipeNet管网流体分析软件[5]、洋葱路由[6]以及第二代洋葱路由Tor[7]通信方案相继实现,并运用到因特网上进行匿名交流。在不允许使用第三方软件的情况下,扩大身份信息破解的空间复杂度和时间复杂度是通信方案中身份隐藏的一般方法,而能否实现则依赖计算的复杂程度。然而,在不久的将来,量子计算机将会面世,其强大的计算能力可以轻易破解当前所有密码算法,新型密码体制将成为主流。基于量子物理特性的安全通信具有无条件安全性,量子安全直接通信、量子签名和量子秘密共享等方案不断被提出。近年来,使用量子方法的匿名通信方案引起了人们的关注。2002年,Boykin[8]将量子机理引入匿名通信协议。之后,关于量子匿名通信的研究也不断被研究者提出[9-12]。Jiang等[13]提出了匿名的量子投票协议。Shi等[14]基于非最大化纠缠量子态在密码学家就餐问题的模型下提出了经典消息量子匿名通信方案。Chen等[15]基于量子混搭纠缠交换原理提出了一个小规模网络中的协作式量子消息匿名通信方案。综上所述,前面已提出的基于量子机制所有协议的局限性在于:参与者不具备自适应性。通信方案中的检测过程和通信过程是2次独立的信号编码,非自适应性的参与者在2次过程中表现一致。自适应是指参与者在通信过程中根据通信的内部外部环境,分析和自动调整通信协议执行规则,改变协议的最终执行结果。此特性可以达到窃取信息和破坏安全性的目的,然而,其行为有可能不被发现。具体地,以前的学者提出的协议中[9-12],自适应性参与者可以在检测过程中遵守协议规定获取信任,却在通信过程中违反协议规定、调整处理方法以求窃取信息。为此,本文作者引入量子连续变量EPR(Einstein-Podolsky-Rosen)态,建立一个新的经典消息匿名通信模型,信道检测过程和消息传输过程合在1次编码中完成,消除参与者是非自适应性的假设限制,提高了方案安全性。利用N+1对纠缠态,实现了N bit消息的匿名传输,达到高效率传输的目的。
1 有关理论
1.1 信息论协议
本方案运用2个经典安全多方计算的定理,它们提供基于信息理论的安全性:定理1(碰撞检测)用于参与者验证他们当中是否只有1个单独的消息发送者,信号会因为有2个以上参与者同时在信道上发送数据叠加造成摆动而增大,也就是说,多个发送者时间上产生了冲突。给信号的摆动值设定1个阀值,超过这个阀值就认为信道发生了冲突;定理2(通知协议)用于消息发送者在若干个参与者中秘密地通知他选择的接收者。
1.1.1 碰撞检测
碰撞检测协议[13]有n个输入值和1个输出值,其中,输入值是n个参与者P1, P2, …, Pn根据自己是或否需要匿名发送信息输入1或0,输出值是对所有输入信息中1的数量的统计,用r表示。很容易预测输出 ,且r为整数。协议正常执行的是r=1,即仅有1个参与者需要匿名发送信息,没有冲突存在;r=0或r>1表示分别存在0个或多个发送者。
,且r为整数。协议正常执行的是r=1,即仅有1个参与者需要匿名发送信息,没有冲突存在;r=0或r>1表示分别存在0个或多个发送者。
1.1.2 通知协议
通知协议[13]是消息发送者用匿名的方式通知接收者。协议的输入是安全计算的参与方的选择,除了参与方各自的输入外,不透露其他任何可用于推导其他输入和输出的信息。各参与方分别产生1个保密输出。若窃听者发动主动攻击,则他唯一可能获得的信息就是这个值。此值反映该参与者是否作为预订的接收者被通知过。
1.2 量子连续变量EPR态
为了达到隐藏消息发送者身份的目的,本方案使用单模电磁场下的量子连续变量EPR纠缠对作为经典信息载体的,用以下公式表示:
 (1)
(1)
根据量子测不准原理,位置 和动量
和动量 符合
符合 ;
; ,
, ,
, 和
和 分别为真空模式下的初始态,它们组成2个模式即模式
分别为真空模式下的初始态,它们组成2个模式即模式 和
和 、模式
、模式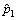 和
和 ,符合
,符合 ,
, 
 。令
。令 ,则式(1)中的
,则式(1)中的 就可以忽略不计,即
就可以忽略不计,即

 (2)
(2)
1.3 有移动式安全多方计算
在本文提出的通信模型中,n个参与者组成环式结构,如图1所示。每个参与者都分别与自己左边、右边的参与者共享1个经过认证的私密量子信道。这样,参与者可以发送量子或经典秘密消息给他的邻居参与者。另外,所有参与者之间还共享经典消息的广播信道,此信道保证所有参与者从发送者那里收到相同的经典消息,且该消息在传输过程中不会被修改。
由定理2,通知的消息接收方制备连续变量纠缠态。之前人们制备的量子态多采用分发方式传输,本文用移动式传输模式,即环式结构中的每个参与者只向左、右参与者接收和传输量子态,从左边参与者接收,编码后发送给邮编的参与者。所有参与者都重复这个过程,直到最后量子态走遍环式结构中的每个参与者回到起点为止。图1所示传输路径反映了这一过程。
每个参与者只接收、操作和发送粒子,从移动传输的粒子中无法推断上一个参与者或下一个参与者的身份。传输的消息被隐藏在若干个纠缠粒子对中,获得完整的秘密消息的方法只有同时拥有多个粒子对。最终,消息接收者测量所有参与安全计算的多方独立输入,并使用持有的纠缠粒子和移动式传输粒子计算秘密消息输入。
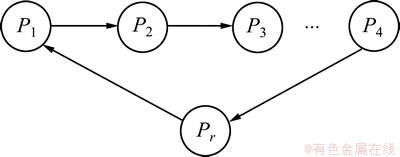
图1 环式结构中的移动传输路径
Fig. 1 Traveling transmission route in ring structure
2 经典消息匿名传输方案
N bit消息编码传输如图2所示。本方案有n个参与者P1, P2, …, Pn,某参与者 想要指定一个消息接收者
想要指定一个消息接收者 ,在Pr不知道消息源情况下传输N bit秘密消息,即N bit消息内容对
,在Pr不知道消息源情况下传输N bit秘密消息,即N bit消息内容对 保密,Ps和Pr的身份信息对
保密,Ps和Pr的身份信息对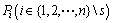 保密,Ps的身份信息对
保密,Ps的身份信息对 保密。
保密。
方案分为以下4步执行。
步骤1:碰撞检测。本方案每一轮由1个消息发送者匿名发送经典消息。参与者P1, P2, …, Pn根据碰撞检测原理共同协作检测在本轮通信中存在多少个参与者,即计算r是否等于1。若r不等于1,则说明产生了碰撞,方案停止执行;若等于1,则方案进入步骤2。
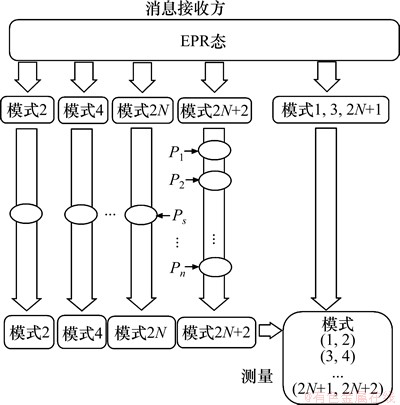
图2 N bit消息编码传输
Fig. 2 Coding and transmitting of N bit message
步骤2:确定接收方。发送者Ps匿名通知他想要发送的接收者Pr,P1, P2, …, Pn共同协作完成通知协议。所有参与者对Ps的身份都未知,仅Ps知道Pr的身份信息。除此之外,没有其他任何身份信息被透漏出来。
步骤3:消息编码。消息接收者Pr制备N+1对量子连续变量EPR态如式(1)。将模式1, 3, …, 2N-1, 2N+1保留在自己手中,模式2, 4, …, 2N+2移动式发送给参与者P1, P2, …, Pn。
编码方式可以描述为
 (3)
(3)
其中: ;
;  和
和 分别表示参与者在位置
分别表示参与者在位置 和动量
和动量 上执行的相位;
上执行的相位; 和
和 为
为 的编码消息,参与者可以调整
的编码消息,参与者可以调整 和
和 ,对于某一轮通信,
,对于某一轮通信, 和
和 为常量。
为常量。
不失一般性,这里 采用相位操作在
采用相位操作在 上编码。若参与者不是消息发送者,则在模式2N+2上编码;若是Ps,则将信息编码在模式2, 4, …, 2N上。
上编码。若参与者不是消息发送者,则在模式2N+2上编码;若是Ps,则将信息编码在模式2, 4, …, 2N上。
参与者的编码方式为
 (4)
(4)
本方案中,模式2对应于传输的N bit消息中的第1位,模式4对应第2位,以此类推,模式2N对应第N位。若参与者是步骤2中通知的Pr,则在对应的模式上编码,消息“1”按照式(4)执行相位操作,消息“0”则不进行任何操作。另一方面,若参与者不是Pr,则在模式2N+2上按照式(4)执行相位操作。最后,所有参与者编码完成,所有量子态到消息接收方时停止传输。模式2, 4, …, 2N,2N+2变成:

同样地,编码方式也可以在动量 上执行。
上执行。
步骤4:消息计算。Pr收到模式2, 4, …,2N,2N+2后,结合模式1, 3, …, 2N-1, 2N+1计算,得到模式2, 4, …,2N,2N+2上编码消息的个数,计算n2, n4, …, n2N+2:


验证 ,若符合,则结果n2n4…n2N即为匿名传送的N bit经典消息,不诚实的参与者人数为
,若符合,则结果n2n4…n2N即为匿名传送的N bit经典消息,不诚实的参与者人数为 。
。
图3所示为匿名通信方案实验构建示意图。为了实现上述方案,搭建了实验平台。使用光学参量振荡器、光分束器和调相调幅器实现N bit经典消息的匿名传输。
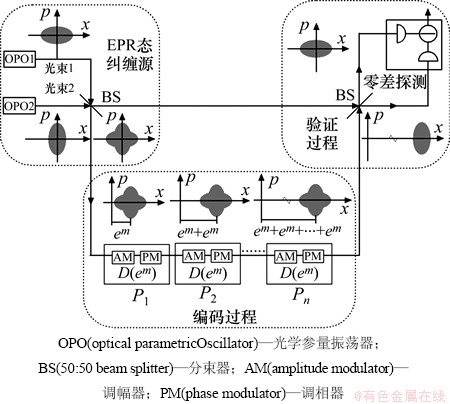
图3 匿名通信方案实验构建图
Fig. 3 Experimental setup for ballot
3 方案讨论和分析
本方案基于安全多方计算,传输消息本身的私密性和消息传输者身份都得到了保护,所以,本文设计方案的安全性极高,能有效防止各种可能的攻击。
3.1 匿名性
步骤1中,外部攻击者A和内部不诚实的参与者有可能在碰撞检测过程中破坏协议的执行。一方面,不诚实的参与者可以使协议终止。例如,他本来的输入为1,也就是说他确实是发送者,但他却输入0,产生输入r=0;反之,若他不是发送者,却置他的输入为1(原本为0),产生输出r>1。即使如此,真实的消息发送者身份无法被窃取。另外,一方面,外部攻击者A除了通过控制若干个不诚实的参与者,让他按照方案执行和输入比特,将参与者的操作告知攻击者A之外,无法获取其他信息。
步骤2中,通知协议(定理2)的运用有效地防止了窃听者对身份安全性的攻击。若因为意外疏忽,发送者通知了非原定的接收者,在执行方案中,就是这个错误通知的接收者而非原定的接收者可以得到匿名传输的经典消息而不被发现。这种消息的私密性被破坏情况仅以指数小的概率发生。即然如此,这个错误的接收者得到的仅是匿名传输的消息,他无法知道在环式结构中此消息到底出自哪一个参与者,所以,Ps的匿名性得到完整保护。
步骤3中,因为本方案是标准的安全多方计算协议,这组参与者遵守约定的方案并共同计算,消息接收者是安全可信的第三方。每个参与者将各自的输入交给消息接收者,由他计算输出值。为了窃取接收者Ps的身份信息,方案攻击者A将发送假连续变量量子态给单个参与者,然后,测量并计算判断这个参与者是否发送了秘密消息。此方法获取信息的概率为1/n,当n很大也就是说参与者数量越多时,用这个方法窃取身份的概率越接近于0。扩大控制的参与者数量是提高成功概率的方法,假定t为攻击者A控制的内部不诚实的参与者个数,则攻击者A正确判断出发送者Ps身份的概率不超过 。
。
步骤4中,主要是检测签名的基于安全多方计算方案中所有协议参与者是否正确地执行涉及的每步运算。消息接收者对接收到的结果进行测量不会对匿名性构成威胁。
3.2 私密性
步骤1、步骤2和步骤4都不涉及秘密消息的传输,所以,不会泄露秘密消息。步骤3中,2种方法可能造成消息的私密性被破坏。
1) 外部攻击者A和内部不诚实的参与者T都可能通过制备或附加另外的纠缠态来发动攻击。基于量子测不准原理和不可克隆原理,只有同时拥有EPR对(模式(1,2)或模式(2N+1, 2N+2))进行测量才能获取信息。虽然模式2, 4, …, 2N+2移动式发送给了参与者,但模式1, 3, …, 2N-1, 2N+1还保留在Pr手中,所以,步骤3的私密性是安全的。
2) 内部不诚实的参与者T可能不遵守通信方案规则而执行非法操作企图更改匿名消息,即修改N bit中某些比特位,可能的非法操作是执行1次负操作或执行2次操作。其中,负操作是指攻击者试图使Ps发送的某一位的值在消息计算时被抵消(由1变成0),于是,他在对应模式上编码-m;同理,执行2次操作能使发送的某一位的值在消息计算时被增加,也就是在对应模式上编码2m。然而,方案中相位操作器使得参与者 只能输入1次控制参数m转化成相位操作
只能输入1次控制参数m转化成相位操作 ,
,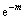 和
和 都会被步骤4检测出来。若不诚实的参与者T(非消息发送者Ps)不在模式2N+2上编码,而是在模式2, 4, …, 2N+2上编码,那么,在步骤4中测量
都会被步骤4检测出来。若不诚实的参与者T(非消息发送者Ps)不在模式2N+2上编码,而是在模式2, 4, …, 2N+2上编码,那么,在步骤4中测量 ,检测结果宣告通信无效。
,检测结果宣告通信无效。
4 方案效率
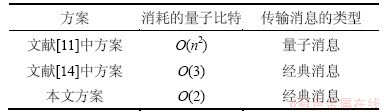
如表1所示,将此方案与已经提出的若干量子匿名通信方案进行对比。以前的方案多采用n个粒子纠缠态产生匿名纠缠信道用于匿名传输消息。然而,当n很大时,现有技术制备参数很大的n个粒子的实验比较困难,而且经济上和效率上都不切实际。为了产生匿名纠缠信道传输1个单位的量子信息,每个参与者在测量过程中消耗1个粒子。此外,每个参与者还需要制备另外n-1个粒子,所以,方案将消耗n(n-1)=O(n2)个粒子。在文献[1]中,3个参与者公布O(3) bit信息用于匿名广播了1 bit经典信息。而本文提出的方案用O(2n)个EPR态粒子匿名传输的(n+1) bit经典消息,方案的效率得到提高。
表1 3种量子匿名通信方案消耗的量子比特对比
Table 1 Comparison of qubits consumed between three quantum anonymous transmission protocols
5 结论
1) 为了保护经典消息传送过程中消息发送者和消息接收者的身份信息,基于量子连续变量EPR态构造了一种安全多方计算模型,移动式传送秘密消息。本方案实现了消息发送者和接收者双方的匿名性,同时还保护了传输消息的私密性。
2) 本方案解决了自适应性参与者的作弊行为,避免了不诚实的参与者在检测过程中诚实却在通信过程中不诚实的问题。
3) 对比DC-NET类匿名广播方案一轮通信仅能传输1 bit消息,此方案利用N+1对量子连续变量EPR态一轮通信可以传输N bit消息,提高了通信效率。
参考文献:
[1] Chaum D. The dining cryptographers problem: Unconditional sender and recipient untraceability[J]. Journal of Cryptology, 1988, 1(1): 65-75.
[2] Franklin M K, Reiter M K. The design and implementation of a secure auction service[J]. Software Engineering, IEEE Transactions on, 1996, 22(5): 302-312.
[3] Berthold O, Federrath H, K psell S. Web MIXes: A system for anonymous and unobservable Internet access[C]// Federrath H. Designing Privacy Enhancing Technologies. Heidelberg: Springer-Verlag, 2001: 115-129.
psell S. Web MIXes: A system for anonymous and unobservable Internet access[C]// Federrath H. Designing Privacy Enhancing Technologies. Heidelberg: Springer-Verlag, 2001: 115-129.
[4] Mitomo M, Kurosawa K. Advances in cryptology: ASIACRYPT 2000[M]. Heidelberg: Springer-Verlag, 2000: 192-204.
[5] Townsend P D. Quantum cryptography on optical fiber networks[C]// Steven P H, Andrew R P. Aerospace/Defense Sensing and Controls. Orlando: International Society for Optics and Photonics, 1998: 2-13.
[6] Reed M G, Syverson P F, Goldschlag D M. Anonymous connections and onion routing[J]. Selected Areas in Communications, IEEE Journal on, 1998, 16(4): 482-494.
[7] Murdoch S J, Danezis G. Low-cost traffic analysis of Tor[C]// Security and Privacy, 2005 IEEE Symposium on. IEEE, 2005: 183-195.
[8] Boykin P O. Information security and quantum mechanics: security of quantum protocols[D]. Los Angeles: University of California. Electrical Engineering Department, 2002: 119-136.
[9] Mueller-Quade J, Imai H. Anonymous oblivious transfer [EB/OL]. [2000-12-03]. http://arxiv.org/pdf/cs/0011004.pdf.
[10] Christandl M, Wehner S. Advances in cryptology-ASIACRYPT 2005[M]. Heidelberg: Springer-Verlag, 2005: 217-235.
[11] Bouda J, Sprojcar J. Anonymous transmission of quantum information[C]// Boyer M. Quantum, Nano, and Micro Technologies, 2007. First International Conference on. Guadeloupe. Caribbean, French: IEEE, 2007: 12.
[12] Brassard G, Broadbent A, Fitzsimons J, et al. Advances in cryptology: ASIACRYPT 2007[M]. Heidelberg: Springer- Verlag, 2007: 460-473.
[13] Jiang L, He G, Nie D, et al. Quantum anonymous voting for continuous variables[J]. Physical Review A, 2012, 85(4): 042309.
[14] SHI Ronghua, SU Qian, GUO Ying, et al. The dining cryptographer problem-based anonymous quantum communication via non-maximally entanglement state analysis[J]. International Journal of Theoretical Physics, 2013, 52(2): 376-384.
[15] CHEN Zhigang, LOU Xiaoping, GUO Ying. A cooperative quantum anonymous transmission with hybrid entanglement swapping[J]. International Journal of Theoretical Physics, 2013: 52(9): 3141-3149.
(编辑 陈灿华)
收稿日期:2013-09-10;修回日期:2014-11-23
基金项目:中南大学中央高校基本科研业务费专项资金资助项目(2012zzts022);国家自然科学基金资助项目(61073186);湖南省教育厅基金资助项目(12C0820);国家留学基金资助项目(201306370086);常德市科学技术局技术研究与开发资金资助项目(2012BS01)
通信作者:陈志刚(1964-),男,湖南益阳人,博士,教授,从事分布式网络研究;电话:13607368966;E-mail: louxiaoping12@gmail.com