J. Cent. South Univ. Technol. (2007)06-0848-05
DOI: 10.1007/s11771-007-0161-6

An HHT-based method to eliminate short-time strong disturbance from measured signals of bridge
WANG Xue-min(王学敏), HUANG Fang-lin(黄方林), MA Guang(马 广), LIU Jian-jun(刘建军)
(School of Civil Engineering and Architecture, Central South University, Changsha 410075, China)
Abstract:According to the characteristic that Hilbert-Huang transform (HHT) can detect abnormity in signals, an HHT-based method to eliminate short-time strong disturbance was proposed. The signal with short-time strong disturbance was decomposed into a series of intrinsic mode functions (IMFs) and a residue by the empirical mode decomposition (EMD). The instantaneous amplitudes and frequencies of each IMF were calculated. And at abnormal section, instantaneous amplitudes and frequencies were fitted according to the data at normal section, replacing the fitted data for the original ones. A new set of IMFs was reconstructed by using the processed instantaneous amplitudes and frequencies. For the residue, abnormal fluctuations could be directly eliminated. And a new signal with the short-time strong disturbance eliminated was reconstructed by superposing all the new IMFs and the residue. The numerical simulation shows that there is a good correlation between the reconstructed signal and the undisturbed signal. The correlation coefficient is equal to 0.999 1. The processing results of the measured strain signal of a bridge with short-time strong disturbance verify the practicability of the method.
Key words: short-time strong disturbance; Hilbert-Huang transform; empirical mode decomposition; instantaneous amplitude; instantaneous frequency
1 Introduction
When carrying out safety monitoring for a bridge, it is needed to install an array of sensors on the bridge to measure structural response signals in some forms of excitation. By processing and analyzing these signals, the current condition of structural safety can be determined. However, in practice, the collection and transmission of the measured signals are liable to be polluted by short-time strong disturbance from environment such as thunder, electrified wire net with high voltage, spatial electromagnetic wave, etc. Under some circumstances, the disturbance can indeed cover the real information entirely and signals with such disturbance used for safety monitoring can cause severe distortion. Therefore, to eliminate short-time strong disturbance from the measured signals is an important and necessary task for safety monitoring.
Generally speaking, eliminating short-time strong disturbance from signals of safety monitoring for a bridge by existing methods, such as filters[1-2] and wavelet analysis[3-5], is very difficult or even impossible because both response signals and disturbance trend to be non-stationary and consist of very wide frequency content, which cannot be determined and distinguished in advance. As a result, the disturbance cannot be effectively removed from the measured signals. Recently, HUANG et al[6] developed a new data analysis technique called Hilbert-Huang transform (HHT) that combines the empirical mode decomposition (EMD) with the Hilbert transform. The most powerful feature of HHT is capable of analyzing nonlinear and non-stationary signals in frequency-time domain. By EMD an arbitrary signal can be decomposed into a series of intrinsic mode functions(IMFs) and each IMF ensures perfect Hilbert transform, accordingly generates physically meaningful instantaneous amplitude and frequency. When a signal involves short-time strong disturbance, its instantaneous amplitudes and frequencies will appear obvious anomalous changes. According to this characteristic, an HHT-based method was presented to eliminate short-time strong disturbance from the measured signals.
2 Brief description of HHT
HHT consists of two main steps: first using EMD to identify IMFs and second to apply the Hilbert transform to each IMF. The algorithm of EMD, designated as the sifting process, is described as follows[7-10].
Step 1 The local extremes of signal x(t) are identified, then all local maxima and local minima are connected by cubic spline lines known as the upper envelope and the lower envelope respectively. The mean of the two envelopes is then computed and subtracted from the original signal x(t). The difference between x(t)
and the mean is the first component h1(t). To check if h1(t) is an IMF, the following two conditions are needed: 1) in the whole data set, the number of zero crossings and extremes must either equal or differ at most by one; and 2) at any point, the mean value of the two envelopes equals zero. If h1(t) does not satisfy criteria 1) and 2), it is treated as x(t) and repeating the above procedure some times until producing the first IMF component, designated as c1(t), which contains the highest oscillation frequencies found in the original signal x(t).
Step 2 The difference between x(t) and c1(t) is treated as a new signal and subjected to the same sifting process as described above, giving the second IMF, c2(t). The EMD procedure continues until the residue becomes so small that it is less than a predetermined value of substantial consequence, or the residue becomes a monotonic function from which no more IMF can be extracted.
Finally, x(t) is expressed as the sum of the IMF components plus the final residue r(t):
 (1)
(1)
Having obtained all the IMFs, the Hilbert transform is applied to each IMF:
 (2)
(2)
where  represents the Hilbert transform of ci(t).
represents the Hilbert transform of ci(t).
Analytic signal is defined as
is defined as
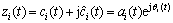 (3)
(3)
where j is the imaginary unit, instantaneous amplitude and phase
and phase are expressed as
are expressed as
 (4)
(4)
 (5)
(5)
Instantaneous frequency is defined as
is defined as
 (6)
(6)
3 Elimination of short-time strong distur- bance
A combined signal x(t), which was the linear sum of normal signal x1(t) and abnormal disturbance x2(t), was selected to illuminate the process of elimination of short-time strong disturbance. The normal signal x1(t) was given by
 (7)
(7)
The abnormal disturbance x2(t) was given by

The waveform of x(t) is shown in Fig.1(a). The sampling frequency was 100 Hz and the time length was 18 s.
With the help of EMD, signal x(t) was decomposed. The extremes extending method in Ref.[11] was used to handle the end effects of EMD. For the purpose of research, EMD procedure was terminated while the main information of frequency and amplitude of normal signal was extracted. By this criterion a total of two IMFs were obtained, as displayed in Figs.1(b) and (c). It can be clearly seen that the two IMFs contain mixed modes[12-13], that is, modes of very different frequencies, which are caused by intermittency occurring in part of the signal. Fig.1(d) shows the curve of residue, which mainly contains the information of disturbance.

Fig.1 Signal x(t) and its decomposition components by EMD
(a) Signal x(t); (b) First IMF; (c) Second IMF; (d) Residue
In Fig.2, the solid lines show the instantaneous amplitudes and frequencies of the two IMFs. It can be seen that the mode mixing leads to obvious abnormity in these curves. To obtain reasonable instantaneous amplitudes and frequencies, these curves were fitted at abnormal sections according to the data at normal

Fig.2 Instantaneous amplitudes and frequencies of two IMFs and their fitted curves
(a) Instantaneous amplitude of first IMF; (b) Instantaneous frequency of first IMF; (c) Instantaneous amplitude of second IMF; (d) Instantaneous frequency of second IMF
sections, replacing the fitted data for the original ones. Considering the concrete form of each curve, instantaneous frequency of the first IMF was fitted into quadratic curve, whereas the others were fitted into straight lines. The fitted results are shown in Fig.2 in dotted lines.
From Eqn.(3),  can be determined by ai(t) and θi(t):
can be determined by ai(t) and θi(t):
 (9)
(9)
From Eqn.(6),  can be written as
can be written as
 (10)
(10)
In actual calculation, the integral initial values can be determined by the normal sections of each phase. Then
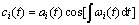 (11)
(11)
By substituting the processed instantaneous amplitudes and frequencies into Eqn.(11), two new IMFs are obtained, as displayed in Figs.3(a) and (b). Clearly, the mode mixing phenomena were overcome. For the residue, since little information of frequency and amplitude of the normal signal are included, the abnormal fluctuations are directly eliminated by fitting data at normal sections. The fitted result is displayed in Fig.3(c). Thus a new signal with the short-time strong disturbance eliminated can be reconstructed by superposing the two new IMFs and the fitted residue, as

Fig.3 Processed results of IMFs (c′1(t) and c′2(t)), residue (r′(t)) and original signal (x′(t))
(a) Reconstructed result of first IMF; (b) Reconstructed result of second IMF; (c) Fitted result of residue; (d) Reconstructed result of signal x(t)
shown in Fig.3(d). In order to show the effect of elimination, Fig.4 shows the comparison between the reconstructed signal and the normal signal in 7-11 s. It can be observed that the reconstructed signal is purified and very close to the normal one. Calculation results indicate that there is a good correlation between the reconstructed signal and the normal signal. The correlation coefficient equals 0.999 1.

Fig.4 Comparison between reconstructed signal and normal signal
4 Application to measured signals
The measured signals were directly taken from the safety monitoring and condition assessment system constructed for Nanjing Yangtze River Bridge (NYRB)[14]. Two model BS-8FT strain gauges, a DH5936 amplifier and a portable computer were used to
measure the strain responses of NYRB when a train was on the bridge. A lot of measured signals were obtained. Fig.5(a) shows one of the measured non-stationary strain signals with short-time strong disturbance of interphone located at a diagonal of the main truss of NYRB. The sampling frequency was 500 Hz and the data length was 6 s. It can be seen that the amplitude of disturbed signal was far greater than that of the normal strain signal.
To eliminate the disturbance, procedures presented above were followed. Firstly, EMD was applied to the measured signal and four IMFs were obtained, as displayed in Figs.5(b)-(e), and Fig.5(f) shows the residue. Then, the instantaneous amplitude and frequency of each IMFs were calculated and fitted, and four new IMF were reconstructed. Taking the second IMF as an example, the instantaneous amplitude and frequency are shown in Fig.6 in solid lines, their fitted curves in dotted lines, and the corresponding reconstructed IMF is shown in Fig.7. After fitting the residue, a new strain signal with the short-time strong disturbance eliminated is finally obtained, as shown in Fig.8.
It can also been seen from Fig.5 that with the continual sifting by EMD, the range of influence of disturbance becomes more extensive. So when a signal has too many IMF components, it is difficult to process the latter components using the presented method. In this case, it is suggested to decompose the normal section directly disregarding the abnormal section, and the fitting is carried out after the instantaneous amplitudes and frequencies are calculated.

Fig.5 Measured strain signal with short-time disturbance and its EMD results
(a) Measured strain signal with short-time disturbance; (b) First IMF;(c) Second IMF; (d) Third IMF; (e) Fourth IMF; (f) Residue

Fig.6 Instantaneous amplitude and frequency of second IMF and their fitted curves
(a) Instantaneous amplitude of second IMF;(b) Instantaneous frequency of second IMF

Fig.7 Reconstructed result of second IMF

Fig.8 Strain signal with short-time disturbance eliminated
5 Conclusions
1) Eliminating short-time strong disturbance from the measured signals of a bridge by existing methods is very difficult or even impossible because of alias or mode mixing.
2) Short-time strong disturbance involved in a signal can cause the instantaneous amplitudes and frequencies to be anomalous. Since the abnormity only exists at local section, it can be eliminated by fitting the normal data. Then the corresponding reconstructed IMF can be purified, consequently the reconstruction of these IMF can get rid of the effect of disturbance. Although the reconstructed signal may not be the exact real signal, it holds main information of amplitudes and frequencies of the real one.
3) The measured signals of safety monitoring for a bridge include short-time disturbance besides useful information, and only when the disturbance is eliminated effectively, analysis results can reflect the real safety condition of the bridge.
References
[1] HU Guang-shu. Digital Signal Processing[M]. Beijing: Tsinghua University Press, 1997. (in Chinese)
[2] ZHANG Xian-da. Modern Signal Processing[M]. Beijing: Tsinghua University Press, 2002. (in Chinese)
[3] DONOHO D L. De-noising by soft thresholding[J]. IEEE Trans on Information Theory, 1995, 41(3): 613-627.
[4] YANG Fu-sheng. The Engineering Analysis and Application of Wavelet Transform[M]. Beijing: Science Press, 1999. (in Chinese)
[5] ZHAO Yong-tao, WANG Yu, GUO Xing-peng. Wavelet transform based-analysis for coulostatically induced transients denoising[J]. Acta Physico-chimica Sinica, 2005, 21(9): 1017-1021. (in Chinese)
[6] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc Royal Society of London Series, 1998, 454: 903-995.
[7] MONTESINOS M E, MU?OZ-COBO J L, P?REZ C. Hilbert-Huang analysis of BWR neutron detector signals: application to DR calculation and to corrupted signal analysis[J]. Annals of Nuclear Energy, 2003, 30: 715-727.
[8] DING Kang, CHEN Jian-lin, SU Xiang-rong. Development in vibration signal analysis and processing methods[J]. Journal of Vibration Engineering, 2003, 16(1): 1-10. (in Chinese)
[9] HUANG N E, WU M L, LONG S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proc Royal Society of London Series, 2003, 459: 2317-2345.
[10] ZHONG You-ming, QIN Shu-ren, TANG Bao-ping. Study on a new transform method for vibration signal[J]. Journal of Vibration Engineering, 2002, 15(2): 233-238. (in Chinese)
[11] HUANG Da-ji, ZHAO Jin-ping, SU Ji-lan. Practical implementation of the Hilbert-Huang transform algorithm[J]. Acta Oceanologica Sinica, 2003, 25(1): 1-11. (in Chinese)
[12] HUANG N E, SHEN Z, LONG S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31: 417-457.
[13] ZHAO Jin-ping. Study on the effects of abnormal events to empirical mode decomposition method and the removal method for abnormal signal[J]. Journal of Ocean University of Qingdao, 2001, 31(6): 805-814. (in Chinese)
[14] HUANG Fang-lin, HE Xu-hui, CHEN Zheng-qing. Structural safety monitoring for Nanjing Yangtze River Bridge[J]. Journal of Central South University of Technology, 2004, 11(3): 332-335.
(Edited by CHEN Wei-ping)
Foundation item: Project (50675230) supported by the National Natural Science Foundation of China
Received date: 2007-03-11; Accepted date: 2007-05-20
Corresponding author: WANG Xue-min, Doctoral candidate; Tel: +86-731-2655039; E-mail: lueac@163.com