J. Cent. South Univ. (2016) 23: 926-933

DOI: 10.1007/s11771-016-3140-y

Viscoelastic micromechanical model for dynamic modulus prediction of asphalt concrete with interface effects

DONG Man-sheng(董满生), GAO Yang-ming(高仰明), LI Ling-lin(李凌林),

WANG Li-na(王利娜), SUN Zhi-bin(孙志彬)

School of Transportation Engineering, Hefei University of Technology, Hefei 230009, China

 Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: A viscoelastic micromechanical model is presented to predict the dynamic modulus of asphalt concrete (AC) and investigate the effect of imperfect interface between asphalt mastic and aggregates on the overall viscoelastic characteristics of AC. The linear spring layer model is introduced to simulate the interface imperfection. Based on the effective medium theory, the viscoelastic micromechanical model is developed by two equivalence processes. The present prediction is compared with available experimental data to verify the developed framework. It is found that the proposed model has the capability to predict the dynamic modulus of AC. Interface effect on the dynamic modulus of AC is discussed using the developed model. It is shown that the interfacial bonding strength has a significant influence on the global mechanical performance of AC, and that continued improvement in surface functionalization is necessary to realize the full potential of aggregates reinforcement.

Key words: asphalt concrete; imperfect interface; rheological properties; micromechanics

1 Introduction

Asphalt concrete (AC) is widely used in the surface layer of flexible pavements. Dynamic modulus of AC has been getting more and more attention in recent years. The dynamic modulus has been incorporated into the National Cooperative Highway Research Program (NCHRP) 1-37A for the American Association of State Highway and Transportation Officials (AASHTO) mechanistic empirical design procedure to guide pavement design [1]. In the NCHRP 9-19 and NCHRP 9-29, the dynamic modulus test has also been selected as a simple performance test to provide fundamental engineering properties of AC [2-3].

There are several available approaches to obtain the dynamic modulus value of AC. The most reliable one is through direct laboratory testing on AC specimens at different temperatures and loading frequencies. However, laboratory testing is usually more time-consuming and expensive than other ways. A micromechanics-based approach provides another possible access to obtaining the dynamic modulus values of AC [4]. This micromechanics approach is based on the fact that AC is actually a particle-reinforced composite composed of three phases: asphalt mastic, aggregates, and air voids. A number of researchers have used finite element method [5-7] and discrete-element method [8-10] to explore the complex micromechanical behavior of AC.

Above proposed micromechanical models do not take into account the interfacial bonding condition between asphalt mastic and aggregate particles. Actually, many factors may affect the interfacial condition, such as thin coating layers, surface chemical reactions between the constituents, irregular shapes of the inclusions, and the processing conditions of mixing and compaction of AC. Therefore, an imperfect interface always exists in AC. This interface imperfection can have a profound influence on the mechanical properties and failure mechanisms of AC [11-12].

The objective of this work is to develop a viscoelastic micromechanical model for the dynamic modulus prediction of AC. The proposed model has the capability of taking into account of the interfacial bonding condition between asphalt mastic and aggregates. The present prediction is compared with available experimental data in the literature to verify the developed model. The effect of imperfect interface on the dynamic modulus of AC is also explored using the present model. This work can help us to better understand the interface effects on the overall viscoelastic characteristics of AC.

2 Constitutive relations of interface and asphalt mastic

AC is actually a particle-reinforced composite composed of three phases: asphalt mastic, aggregates, and air voids, (see Fig. 1). In the particle-reinforced composite system, asphalt mastic will be referred to as the matrix phase, and aggregates as the inhomogeneity phase. Aggregate particles are very stiff and their mechanical response can be considered predominantly elastic. Asphalt mastic will be modeled as viscoelastic and its behavior will be represented by Burgers four-parameter model. The condition of imperfect load transfer will be modeled by a displacement jump. Though the interface has zero volume concentration, the displacement jump can significantly lower the overall strength of the particle-reinforced composite.

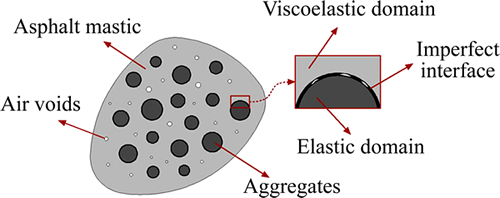
Fig. 1 Micromechanical model for AC with imperfect interface

2.1 Imperfect interface modeling

Consider an elastic inhomogeneity Ω embedded in a different elastic domain D. Let S denote the interface between the inhomogeneity and the matrix. For perfect interface, the displacement and traction fields are both continuous across this interface, and the continuity of displacement and traction can be written as

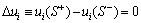                       (1)

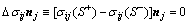               (2)

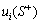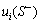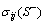where n_j is the unit outward normal vector of the interface S;  and  are the values evaluated at the positive side of S; while  and  are the values evaluated at the negative side of S. It is assumed that the positive side of S is the side to which n_j points.

However, an imperfect interface could undergo a displacement jump. The present work will follow the linear spring layer model proposed by Benveniste [13], Hashin [14], and Qu [15-16]. In this model, the interfacial traction continuity is maintained, but displacement discontinuity may occur at the interface. The displacement jump at the interface is related to the interfacial traction, and the interface conditions can be written as

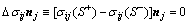               (3)

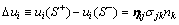                 (4)

where η_ij is a second-rank tensor representing the spring compliance of the interface. For simplicity, it is assumed that η_ij is symmetric and positive definite. It is clear from Eq. (4) that η_ij=0 corresponds to a perfect interface, while 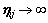 represents complete debonded. The physical significance of η_ij can be given by adopting the following form:

                        (5)

where  is the Kronecker delta, and α and β represent the tangential and normal compliances of the interfaces, respectively, i.e.

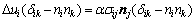              (6)

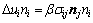                             (7)

When 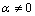 and 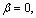 such constitutive characterization of the interfaces allows for tangential sliding between the two surfaces, but not normal separation or interpenetration. This condition will be assumed in this work. Therefore, the influence of α on the overall viscoelastic properties of the composite is concerned. It is clear that α=0 stands for perfectly bonded interface and  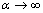completely debonded interface.

2.2 Viscoelastic constitutive equations of asphalt mastic

Since the behavior of viscoelastic matrix departures from the ideal Hooke body or ideal Newton body, rheological models can be used to describe the viscoelastic characteristics of the real materials approximately. For the description of asphalt mastic considered later, the four-parameter Burgers model (see Fig. 2) is selected among many candidate models to fit the lab test data due to its precision and mathematical efficiency, and its governing differential equation is given as

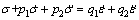                      (8)

with

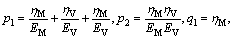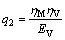 and                              (9)

where E_M, E_V are the elastic parameters and η_M, η_V are the viscous parameters to be determined.

2.2.1 Transformed modulus in Laplace domain

As we all know, the Laplace transform method is the most commonly used method to deal with the linear viscoelastic problem [17-18], and leads to the possibility of establishing a correspondence between viscoelastic problem and elastic problem. The Laplace transform of a function, f(t), is given by

                          (10)

Applying this transform to the viscoelastic constitutive equation, Hooke’s law in the transformed domain can be expressed as [19-20]

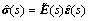                             (11)

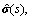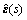where  and  are the Laplace transform of the stress and strain tensors, respectively; and  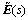is the modulus tensor in the transformed domain.

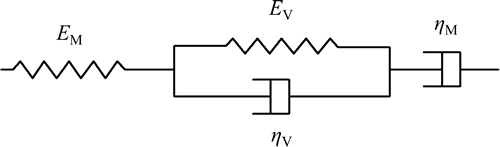
Fig. 2 Burgers model for viscoelastic asphalt mastic matrix

After carrying out Laplace transform, the elastic modulus of Burgers model in the transformed domain is given as

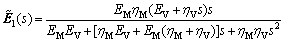 (12)

2.2.2 Complex modulus under harmonic loading

The complex modulus is involved to investigate storage and loss modulus under harmonic loading. This issue is particularly important for long-term reliability of AC. Now, if the asphalt mastic is subjected to the cyclic loading 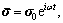 its steady state strain will also be harmonic and can be written as  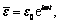where 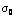 and ε₀ are the amplitudes of the stress and strain tensors of the asphalt mastic, and i and ω are the imaginary number and angular frequency, respectively. The relation of the amplitudes of the stress and strain tensors can be described as  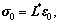where L^* is the complex modulus tensor of the asphalt mastic. Since the time-rate of the stress or strain under harmonic loading produces a coefficient iω, and the Laplace transform of the stress rate or strain rate produces a coefficient s, the complex modulus naturally has an identical expression to the transformed modulus in the Laplace domain, with iω replacing s [21-22]. For the Burgers model, the complex elastic modulus in the frequency domain can be expressed as

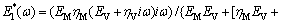
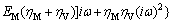          (13)

3 Viscoelastic micromechanical modeling

As mentioned previously, AC can be regarded as a composite with aggregate particles and air voids dispersed in the asphalt mastic matrix. The same concept of effective medium as used by Eshelby [23] and Christensen [24] is employed.

3.1 Effective elastic modulus of AC with interface effect

For AC consisting of an isotropic asphalt mastic matrix with stiffness tensor L₁ and isotropic, spherical aggregate particles of stiffness tensor L₂, the effective properties of AC become isotropic. The interface between aggregate particles and asphalt mastic matrix is described by the displacement jump condition Eq. (4) where

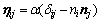                           (14)

With the imperfect interface, Eshelby’s tensor S has been modified to S^M by Qu [15-16] to account for the effect of interface sliding parameter α as

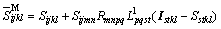          (15)

where 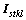 is the fourth order identity tensor, and

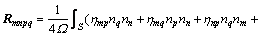
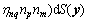                      (16)

depends on the interface properties through η_ij and the geometry of the aggregate particles. The explicit form of 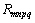 is given in Ref. [16].

With this modified Eshelby’s tensor S^M and making use of the modified Mori-Tanaka method [25-26], the effective bulk and shear moduli of AC with an imperfect interface can be rewritten as

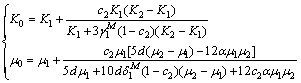             (17)

where

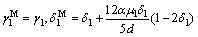             (18)

with

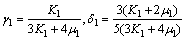               (19)

K₂, μ₂, K₁ and μ₁ represent the bulk and shear moduli of aggregate and asphalt mastic, and c₂ and d are the volume fraction and diameter of aggregate particle, respectively. Further, the effective elastic modulus corresponding to aggregate particle size d can be obtained by

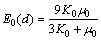                            (20)

From Eq. (20), a specific elastic modulus can be gained corresponding to a specific single particle size d of aggregate particle. However, the different particle sizes for AC are always used to acquire the satisfactory aggregate gradation. Every aggregate particle of specified size makes its own contribution to the effective elastic modulus of AC. Accounting for the size distribution of aggregate gradation, the effective elastic modulus of AC is expressed as

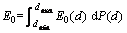                       (21)

where d_min and d_max are the minimum and maximum aggregate particle diameters, respectively.

Integrating Eq. (21) is very difficult due to the complex mathematical expressions E₀(d) and P(d). Instead, Eq. (21) can be approximated by a numerical summation as follows [5, 24, 27]:

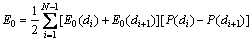    (22)

where E₀(d_i) and E₀(d_i+1) are the effective elastic moduli corresponding to aggregate particle diameters d_i and d_i+1, respectively.

3.2 Linear viscoelastic conversion from elastic solutions

Based on the elastic-viscoelastic correspondence principle, Eq. (17) can be expressed in the Laplace transform domain as follows:

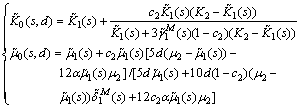
 (23)

The transformed bulk and shear moduli, 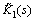 and  of the asphalt mastic matrix are related to 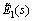 and transformed Poisson ratio  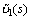through

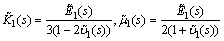         (24)

These two constants, as well as the other two involving  and 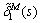 in Eq. (23), are all functions of the Laplace parameter s. The transformed  and 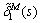 have identical expressions as the original  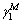and  but each component of the matrix modulus, such as E₁ or K₁, must be replaced by its transformed counterpart, 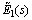 or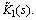

The stress-strain relations of the asphalt mastic matrix under harmonic loading as described in Section 2.2.2 also hold for the overall AC. Therefore, Eq. (23) can be expressed in the frequency domain as follows:

        (25)

the effective complex modulus in the low frequency range corresponding to aggregate particle size d can be obtained by

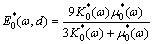                    (26)

Considering aggregate gradation, the effective complex modulus of AC with interface effect can be expressed as

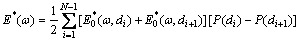            (27)

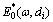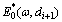where  and  are the effective complex moduli corresponding to aggregate particle diameter d_i and d_i+1, respectively; and  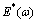can be written as

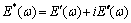                       (28)

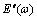where  and  are the effective storage and loss moduli, respectively.

Finally, the dynamic modulus and phase angle can be respectively obtained as

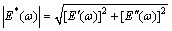                 (29)

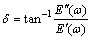                             (30)

3.3 Consideration of air voids

Air voids are one of the important constitutions of AC, and have a significant effect on the mechanical properties of AC. To better characterize AC, both the air voids size distribution and air voids content should be incorporated in the prediction model. Figure 3 presents the typical air voids size distributions [4, 11] used in this study. It is assumed that the air voids are all circular inclusions [11, 28-30], and only coarse air voids (diameter≥1.4 mm) are considered in the developed model.

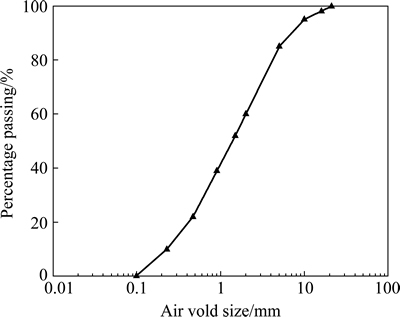
Fig. 3 Air void size distribution in AC

In order to account for air voids in the proposed model, the dynamic modulus of AC can be obtained by using a two-step method as shown in Fig. 4. In the first step, air voids are neglected and the dynamic modulus value is obtained for AC without air voids. In the second step, the air void bubbles entrapped in AC are assumed to be a series of empty spheres of different sizes covered with the same thickness of the effective medium obtained from the first step. The dynamic modulus of AC with air voids is obtained by using the similar procedure for considering aggregate gradation.

The procedure used for the aggregate gradation in AC is applied to the air voids size distribution, and zero modulus is used for air voids. Using Eq. (22) once again, the dynamic modulus of AC containing air voids can be finally obtained.

4 Results and discussion

To verify the feasibility of the present framework, a comparison between the theoretical results and available experimental data is conducted. It is also intended to further investigate the effect of interface on the viscoelastic characteristics of AC.

The present predictions are compared with experimental data reported by You and Buttlar [31] for the dynamic modulus of AC. Aggregates in AC are modeled as spherical particles in this simulation. The Poisson ratios of asphalt mastic and aggregates are assumed to be 0.4 and 0.2 in the present calculation, respectively [21, 27, 30, 32]. According to Ref. [31], ACspecimens with 4.8% asphalt content by weight were compacted in a superpave gyratory compactor (SGC) to a target air void level of 4% by volume. The aggregate gradation and volume fractions are listed in Table 1 [31, 33]. Elastic modulus of aggregates is taken as 55.5 GPa [31, 33]. Elastic mastic had a nominal maximum aggregate size of 1.18 mm and around 14% asphalt content by weight. Laboratory test results of asphalt mastic and AC at 0 °C are listed in Table 2 [31, 33]. Using the procedure developed by Liu et al [33], Burgers model parameters for asphalt mastic are then obtained, and listed in Table 3. Then, these material parameters are further adopted to predict the dynamic modulus and phase angles of AC.

4.1 Comparison between predicted and measured results

The comparison between the theoretical results and available experimental data is presented in Fig. 5. It is observed that the predicted dynamic modulus values are substantially larger than the test data when the aggregate is perfectly bonded by asphalt mastic (namely, α=0). However, when the aggregate is gradually debonded from asphalt mastic, namely, the value of α increases gradually, the dynamic modulus values will decrease correspondingly. It is seen from the figure that when α=10^-4, the predicted curve agrees well with the experimental data. It can be concluded that a slightly weakened interface existing between asphalt mastic and aggregates may reduce the dynamic modulus of AC. Another situation is found that the dynamic modulus curve of α=10^-2 is quite close to the curve of α=10^-1, since α=10^-2 and α=10^-1 represent a rather weak interface and at such interface, the aggregates never work as reinforced materials. It can be thus concluded that the measured dynamic modulus data cannot be well captured without considering the effect of imperfect interface, and that an imperfect interface model should be adopted in the effective medium theory to describe the viscoelastic characteristics of AC.

4.2 Parameters influencing dynamic modulus of AC

4.2.1 Influence of imperfect interface

Using the developed viscoelastic micromechanical method, the dynamic modulus values of AC under different interface parameters are also calculated. The results are plotted in Fig. 6. It is noted that the dynamic modulus is sensitive to α. Besides, it is concluded that the effect of imperfect interface on the dynamic modulus of AC can be separated into five zones. Zone I corresponds to the strong interface (0≤α<10^-5). In this zone, the dynamic modulus value reaches the maximum. The dynamic modulus value no longer increases with the decrease of α, which indicates that a stronger interface will little affect the overall performance of AC. Zone II corresponds to the value of 10^-5≤α<10^-4. In this zone, the dynamic modulus value decreases slowly with the increase of α, which means that a certain extent interface imperfection can be accepted, and will not significantly influence the material performance. Zone III corresponds to the value of 10^-4≤α<10^-2. In this zone, the dynamic modulus value decreases rapidly with the increase of α, which shows that with a weaker interface, a looser interaction will occur between asphalt mastic and aggregates, and the stiff aggregates will have less opportunities to contribute themselves to the overall viscoelastic properties of AC. Therefore, a weak interface will result in the bad performance of AC. Zone IV corresponds to a relatively large value of 10^-2≤α<10^-1. In this zone, the dynamic modulus value decreases slowly with the increase of α again, which implies that the stiff aggregates surrounded by a relatively weak interface behave like the soft materials. The final zone is Zone V, which corresponds to a very weak interface (10^-1≤α). In this zone, the dynamic modulus value reaches the minimum. The dynamic modulus value no longer decreases with the increase of α since the aggregate is almost totally debonded from asphalt mastic, which demonstrates that the stiff aggregate never works as a reinforced material.

Fig. 4 Two-step method for AC

Table 1 aggregate gradation and volume fractions for AC

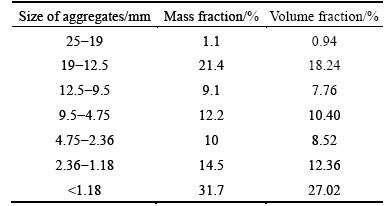
Table 2 Laboratory test results of asphalt mastic and AC at 0 °C

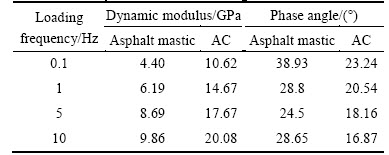
Table 3 Burgers model parameters fitted using lab data

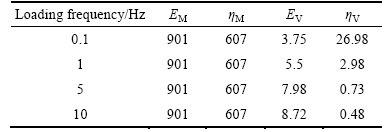
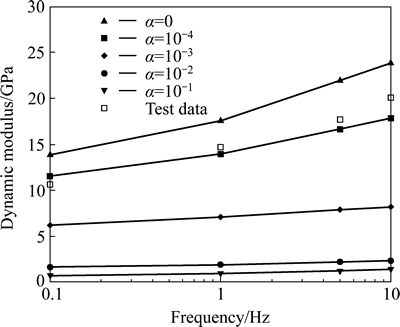
Fig. 5 Comparison of predicted and measured dynamic modulus value

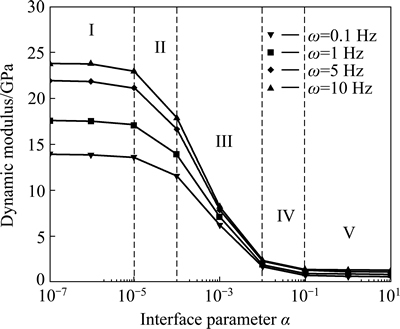
Fig. 6 Effect of imperfect interface on dynamic modulus of AC

4.2.2 Influence of elastic property of aggregates

The effect of the elastic modulus of aggregates on the dynamic modulus under various interface parameters is presented in Fig. 7. It can be found that with a strong interface (α=0 and α=10^-4), the elastic modulus of aggregates greatly affects the dynamic modulus of AC. Especially at the initial stage, the dynamic modulus increases rapidly with the increase of the elastic modulus, which means that the aggregate works as a reinforced material when it is tightly bonded with asphalt mastic. However, after the elastic modulus reaches 70 GPa, the variation of the dynamic modulus becomes stable,which indicates that the contribution of aggregates to the dynamic modulus improvement of AC is limited. On the contrary, with a weak interface (α=10^-2 and α=1), the elastic modulus of aggregates has little effect on the dynamic modulus of AC. At the initial stage, only a slight change occurs. The stiff aggregate never works as a reinforced material when the interface parameter tends to large values. Therefore, when the aggregate is surrounded by a weak interface, it is useless to improve the overall properties of AC by enhancing its stiffness.

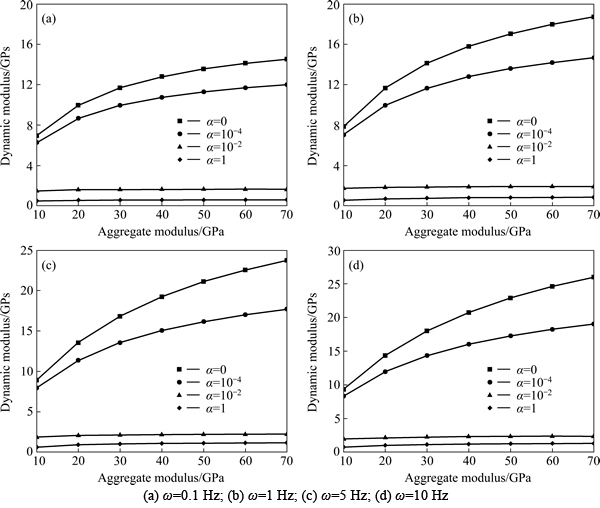
Fig. 7 Effect of elastic modulus of aggregates on dynamic modulus of AC:

5 Conclusions

1) Based on the linear spring layer model and the effective medium theory, a viscoelastic micromechanical model for dynamic modulus prediction of AC with imperfect interface is proposed by two equivalence processes. The present prediction when α=10^-4 is observed to be in good agreement with the experimental data in the literature.

2) The influence of interface parameter α on the dynamic modulus of AC is quite significant. It can be separated into five different zones, and the variation of dynamic modulus value presents different characteristics at each zone.

3) The elastic modulus of aggregate greatly affects the dynamic modulus value of AC with a strong interface. However, the elastic modulus of aggregate has little effect on the dynamic modulus of AC with a weak interface.

4) The interfacial bonding strength between asphalt mastic and aggregates does have a significant influence on global viscoelastic properties of AC.

References

[1] ANDREI D, WITCZAK M W, MIRZA M W. Development of a revised predictive model for the dynamic (complex) modulus of asphalt mixtures [R]. NCHRP 1-37A, Inter Team Report, University of Maryland, 1999.

[2] National Cooperative Highway Research Program. Simple performance test for superpave mix design [R]. NCHRP 9-19, Interim Report, National Research Council, 2003.

[3] BONAQUIST R. Simple performance tester for superpave mix design [K]. NCHRP 9-29, Quarterly Progress Report (Appendix B), 2003.

[4] SHU Xiang, HUANG Bao-shan. Micromechanics-based dynamic modulus prediction of polymeric asphalt concrete mixtures [J]. Composites Part B: Engineering, 2008, 39: 704-713.

[5] HUANG Bao-shan, ASCE M, SHU Xiang, LI Guo-qiang, CHEN Lei-shang. Analytical modeling of three-layered HMA mixtures [J]. International Journal of Geomechanics, 2007, 7: 140-148.

[6] DAI Qing-li. Two- and three-dimensional micromechanical viscoelastic finite element modeling of stone-based materials with X-ray computed tomography images [J]. Construction and Building Materials, 2011, 25: 1102-1114.

[7] CHEN Ye-kai, YU Jiang-miao, ZHANG Xiao-ning. Micromechanical analysis of damage evolution in splitting test of asphalt mixtures [J]. Journal of Central South University of Technology, 2010, 17: 628-634.

[8] CHEN Jun, WANG Lin-bing, HUANG Xiao-ming. Micromechanical modeling of asphalt concrete fracture using a user-defined three-dimensional discrete element method [J]. Journal of Central South University, 2012, 19: 3595-3602.

[9] YU Hua-nan, SHEN Shi-hui. A micromechanical based three-dimensional DEM approach to characterize the complex modulus of asphalt mixtures [J]. Construction and Building Materials, 2013, 38: 1089-1096.

[10] DONDI G, VIGNALI V, PETTINARI M, MAZZOTTA F, SIMONE A, SANGIORGI C. Modeling the DSR complex shear modulus of asphalt binder using 3D discrete element approach [J]. Construction and Building Materials, 2014, 54: 236-246.

[11] ZHU Xing-yi, CHEN Long. Numerical prediction of elastic modulus of asphalt concrete with imperfect bonding [J]. Construction and Building Materials, 2012, 35: 45-51.

[12] ZHU Xing-yi, WANG Xin-fei, Yu Ying. Micromechanical creep models for asphalt-based multi-phase particle-reinforced composites with viscoelastic imperfect interface [J]. International Journal of Engineering Science, 2014, 76: 34-46.

[13] BENVENISTE Y. The effective mechanical behavior of composite materials with imperfect contact between the constituents [J]. Mechanics of Materials, 1985, 4: 197-208.

[14] HASHIN Z. Thermoelastic properties of fiber composites with imperfect interface [J]. Mechanics of Materials, 1990, 8: 333-348.

[15] QU Jian-min. Eshelby tensor for an elastic inclusion with slightly weakened interface [J]. Journal of Applied Mechanics, 1993a, 60: 1048-1050.

[16] QU Jian-min. The effect of slightly weakened interfaces on the overall elastic properties of composite materials [J]. Mechanics of Materials, 1993b, 14: 269-281.

[17] RIZZO F J, SHIPPY D J. An application of the correspondence principle of linear viscoelasticity theory [J]. SIAM Journal on Applied Mathematics, 1971, 21: 321-330.

[18] SIM W J, KWAK B M. Linear viscoelastic analysis in times domain by boundary element method [J]. Computers & Structures, 1988, 29: 531-537.

[19] TSCHOEGL N W. The phenomenological theory of linear viscoelastic behavior [M]. Berlin: Springer, 1989.

[20] KIM Y R, LITTLE D N. Linear viscoelastic analysis of asphalt mastics [J]. Journal of Materials in Civil Engineering, 2004, 16: 122-132.

[21] SHU Xiang, HUANG Bao-shan. Dynamic modulus prediction of HMA mixtures based on the viscoelastic micromechanical model [J]. Journal of Materials in Civil Engineering, 2008, 20: 530-538.

[22] PAN Y, WENG G J, MEGUID S A, BAO W S, ZHU Z H, HAMOUDA A M S. Interface effects on the viscoelastic characteristics of carbon nanotube polymer matrix composites [J]. Mechanics of Materials, 2013, 58: 1-11.

[23] ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion, and related problems [J]. Proceedings of the Royal Society of London Series A: Mathematical and Physical Sciences, 1957, 241: 376-396.

[24] CHRISTENSEN R M. Mechanics of composite materials [M]. New York: Wiley, 1979.

[25] MORI T, TANAKA K. Average stress in matrix and average elastic energy of materials with misfitting inclusions [J]. Acta Metallurgica, 1973, 21(5): 571-574.

[26] Qu Jian-min, CHERKAOUI M. Fundamentals of micromechanics of solids [M]. New Jersey: John Wiley & Sons, Inc, 2006.

[27] LI Guo-qiang, LI Yong-qi, METCALF J B, PANG Su-seng. Elastic modulus prediction of asphalt concrete [J]. Journal of Materials in Civil Engineering, 1999, 11: 236-241.

[28] ANDERSON D A, GOETZ W H. Mechanical Behavior and reinforcement of Mineral Filler-Asphalt Mixtures [J]. Journal of the Association of Asphalt Paving Technologists, 1973, 42: 37-66.

[29] BUTTLAR W G, BOZKURT D, AL-KHATEEB G G, WALDHOFF A S. Understanding asphalt mastic behavior through micromechanics [J]. Transportation Research Record: Journal of the Transportation Board, 1999, 1681: 157-169.

[30] LI Yong-qi, METCALF J B. Two-step approach to prediction of asphalt concrete modulus from two-phase micromechanical models [J].Journal of Materials in Civil Engineering,2005, 17: 407-415.

[31] YOU Z, BUTTLAR W G. Micromechanical modeling approach to predict compressive dynamic moduli of asphalt mixture using the distinct element method [J]. Transportation Research Record: Journal of the Transportation Research Board, 2006, 1970(1): 73-83.

[32] Zhu Xing-yi, Yang Zhong-xuan, Guo Xing-ming, Chen Wei-qiu. Modulus prediction of asphalt concrete with imperfect bonding between aggregate-asphalt mastic [J]. Composites: Part B, 2011, 42: 1404-1411.

[33] LIU Yu, DAI Qing-li, YOU Zhan-ping. Viscoelastic model for discrete element simulation of asphalt mixtures [J]. Journal of Engineering Mechanics, 2009, 135: 324-333.

(Edited by YANG Hua)

Foundation item: Project(51408173) supported by the National Natural Science Foundation of China

Received date: 2015-04-08; Accepted date: 2015-09-23

Corresponding author: DONG Man-sheng, Associate Professor, PhD; Tel: +86-13805601142; E-mail: dongms@hfut.edu.cn