文章编号:1004-0609(2008)07-1317-06
本征超导态的理论分析和计算超导临界温度Tc新方法
邹壮辉,周志敏,王明光,马常祥,祁 阳
(东北大学 理学院,沈阳 110004)
摘 要:把材料的超导态作为不依赖于载流子类型和传导方式而存在的本征态,利用正常态的量子固体理论导出超导临界温度Tc的计算公式,对13种计算所需参数齐全的超导元素Tc值的计算结果,除Nb和Sn的误差偏大之外,其余11种元素的计算Tc值和实验值吻合。全部计算Tc值随原子序数的起伏规律和测量Tc值的相同。超导电性判据适用于元素周期表中除了La系、Ac系和Rf、Ha和Unh之外的所有导电元素。计算只需要使用材料的常温下参数,可以判定新材料是否超导并预测其Tc值,提出一个超导电性物理本质的新观点。
关键词:超导材料;临界温度;本征超导态;超导理论
中图分类号:O 48;TG 14 文献标识码:A
Analysis of intrinsic superconductive state and calculation method of superconductive critical temperature
ZOU Zhuang-hui, ZHOU Zhi-min, WANG Ming-guang, MA Chang-xiang, QI Yang
(College of Science, Northeastern University, Shenyang 110004, China)
Abstract: The superconductive state of materials was taken for an intrinsic state of materials, which is independent of the charge carrier or its type. A formula of the critical temperature Tc of superconductive materials was established using ordinary quantum solid-state theory. For these 13 superconductive elements with full parameters for calculation, the calculated critical temperatures are consistent with experimental value except for Nb and Sn. A criterion for distinguishing superconductive element is obtained. The criterion is valid for all the elements except for the La, Ac system and non-conducting elements in the Periodic Table. A new viewpoint is advanced on the natural instinct of superconductivity.
Key words: superconductivity materials; critical temperature; intrinsic superconductive state; superconductive state theory
材料超导电性被发现近一个世纪以来,陆续发表有较大影响的超导理论或模型近20个,而对这些理论进行修改或补充的次级模型数量则难以统计。然而,一些超导材料的出现却脱离理论预期,如氧化物高温超导材料[1?2]、二硼化镁等超导化合物[3]、有机聚合物(P3HT)超导材料[4]以及掺杂C60高温超导材料等[5]。理论不能预测实验结果,甚至与其相背离的问题迫切需要解决。20世纪80年代中期,ANDERSON提出了高温超导理论,在超导领域继1957年BCS理论之后第二次获得诺贝尔物理学奖。然而,另一位诺贝尔奖得主LANGHLIN否定了Anderson理论,于2002年又提出了Gossamer超导理论,认为单带模型不能做为高温超导理论的出发点。2003年,ANDERSON又提出了RVB-Plain Vanilla超导理论,用有效单带模型及RVB(共振价键)波函数的变分计算得到了超导态相图,并把Gossamer理论包含其中,认为这是完整的高温超导理论。该理论发表不到一年,即遭到BELL实验室Varma的全面否定。至此,超导理论成为先后两次颁发诺贝尔奖而最新结果却是错误的这样一道世界难题。2004年以来,未见新的超导理论或模型发表,仅有些在BCS理论、朗道理论和Anderson理论基础上的补充性或验证性研究[6]。在研究方面,追求高临界温度(Tc)新材料的研究陷入困境,而二硼化镁制备和掺杂[7?9]、Bi系薄膜及带材制备[10?11]、YBCO纳米颗粒掺杂及涂层薄膜制备等应用研究较活跃[12]。超导薄膜的表面特性为超导器件的发展拓展了空间,也对已有的理论提出了新的问题。以电子对等载流子为基础的超导理论所不能解决的问题,可能属于材料低温状态方面的问题,而不属于载流状态或载流子种类和行为问题。因此,本文作者提出本征超导态(或空超导态)概念,建立了新的模型,利用一般固体理论导出超导临界温度计算公式和材料超导态判据,比较了计算结果和实验结果,并分析了其误差。目的是探索超导电性物理本质及普适性规律,更好地引导高Tc新超导材料研究开发。
1 问题的提出
在已有的超导理论中,除了Genzberg-Landau (G-L)理论外,都采用了不尽相同的超导载流子建立超导模型,如Cooper对等。以著名的BCS理论为例,它提出的双电子系统Schr?dinger方程为[13]

式(1)和(2)描述电子对的传输状态,它确定的超导态依赖于电子对的存在和电子对的散射。如果超导体处于没通电状态,也就没有了电子对和电子对的被散射,所描述的材料超导态也就不存在了。用激子、双极化子、费米液体、自旋袋和重费米子等其它超导载流子建立的模型也同样只适合描述载流超导态[14?15]。G-L理论虽然是从材料的相变过程建立超导模型,但在它的第二方程中引进了超导电流Is,导致特征长度L(T)和相干长度l(T)这类和传导过程有关的参数出现,也是描述载流超导态的。显然,已有的超导理论都是描述载流子传输状态的,不适合描述非载流状态。建立这些理论是先假定了材料超导,不能用于判定材料是否具有超导电性,也不适合预测超导材料的成分结构特征以及材料参数计算。由此可见,超导理论研究两个大的方向存在很大差别:一是研究载流超导态,需要先假定材料超导并设定载流子类型,偏向于量子电动力学方向,解决超导传输及器件开发应用问题;二是研究材料的本征超导态,不做材料是否超导的假定,仅在广义假定无散射条件,偏向于量子固体理论方向,解决超导材料的成分结构预测和提高材料超导性能问题。
本征超导态或空超导态是指材料中没有通电的超导状态。自从确立了低温下材料的完全抗磁性为材料是否具有超导电性的实验判据之后,认定材料是否超导的实验大多是在非载流状态下进行的,这证明空超导态存在。空超导态是材料的固有状态,只涉及不同温度下材料状态和成分、结构间的关系,并不涉及载流子行为和载流过程,这种条件下Schr?dinger方程的求解在固体理论中已经解决[16],这些理论在常温和低温条件下都是适用的。
2 理论模型和计算
2.1 本征超导态模型的一般描述
2.1.1 零电阻条件
导体电阻由散射引起。单纯从材料状态考虑,只需要确定材料在什么状态下不会对传导电子形成散射,该状态就是材料的本征超导态;而判定某种材料是否存在无散射状态,则可能确定其是否具有超导电性。
按照量子力学的描述,传导电子受到离子势场和近邻以及次近邻离子间势场重叠处势井的散射,并假定材料内部是被离子势场充满,而传导电子可以以任意路径穿过导体。因此,不发生散射应当满足下列条件:1) 各离子势场被限制在足够小的范围内;2) 近邻离子间势场重叠处的势井接近于点状势井,次近邻离子间势井消失;3) 离子势场对传导电子迁移路径予以限制,电子不能以任意路径穿过导体。
2.1.2 基本假定及其推论
根据零电阻条件和低温下价电子的平均能量降低、离子的热振动振幅减小的特征。对材料本征超导态做以下假定:1) 在低温下,价电子由于能量降低而收缩在一个靠近费米面的、相当于常温下某一较低能级价电子Ei所对应的极薄球壳内,传导电子在该球壳内迁移不会受到离子和势井的散射,电阻消失;2) 离子势场收缩导致次近邻离子间势井的消失,使价电子成键态几率减少而传导态几率增加,载流密度增大。得到推论为:1) 某种材料是否具有超导电性或超导临界温度的高低主要取决于其价电子能级结构;2) 超导材料载流密度大小主要取决于材料在温度降低时有多少次近邻势井消失,结构复杂的多元超导材料应该具有较高载流密度。
2.2 超导临界温度Tc的计算公式和计算结果
2.2.1 计算公式的导出
在正常态下,求解定态Schr?dinger方程(自由电子近似)并应用费米—狄拉克统计可得价电子的平均能量E为[16]

由式(4)和(5)可得价电子只与温度有关的平均能量为

当温度由常温T降低到Tc时,所有价电子的能量都降低到 附近薄球壳内,降温产生的电子平均能量差为
附近薄球壳内,降温产生的电子平均能量差为 。作为价电子
。作为价电子
能级参数的电离能在降低温度时也会发生改变,最外层价电子的电离能在常温下为E1,在Tc温度下则处于常温时某一内层价电子电离能Ei的水平,可得
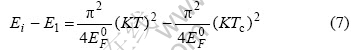
上式是只考虑材料状态的结果,还需要根据转变过程做修正。引进无穷小量?T,认为超导转变仅发生在Tc+?T区间。材料从常温被冷却到Tc+?T,并不发生超导转变,但对应的能量差对于超导转变是有贡献的,只是式(7)不能包含这个意义。因此,把材料从常温T降低到Tc时产生的电子能量差全部加到0~(Tc+?T)内,引进结构参数γ,可得
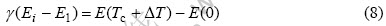
式中 E1和Ei为第1级和第i级电离能;γ为与材料晶体结构及缺陷有关的待定系数。等号左边是降温产生的实际电子能量差,等号右边是实现超导转变所需要的临界电子能量差,其意义是把材料从T降温到Tc产生的电子能量差施加于发生超导转变的温区,相当于加权处理。这是处理相变问题时常见的方法。
对于某种具体材料,当温度由0上升到Tc+?T时,价电子能量由E(0)=0增加为E(Tc+?T)。尽管?T是一个无穷小量,但超导电性刚好被破坏而进入正常态,由式(6)可知这时价电子能量为
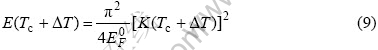
发生超导态和正常态转变(温度从0上升到Tc+?T)所对应的价电子能量差为
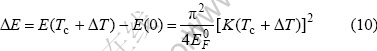
略去无穷小量?T,上式写成

原子配位数不能惟一反映材料的结构差异(如fcc结构和hcp结构的原子配位数相同),选择与原子密排面相关的有效价电子路径数neff来确定γ。任选某种已知Tc值超导材料的有关数据代入式(13),试解一元n次待定系数方程可得

由式(13)和(14)得出结晶完整的超导体临界温度Tc计算公式:

考虑处在填满的d能级价电子一般不参与导电、各能级电子数奇偶性对轨道角动量对称性的影响等因素,确定Ne的取值规则:1) 最外层和次外层能级电子数有奇有偶,Ne为两能级上价电子数之和乘以阿伏加德罗常数N,如V的外围电子结构为3d34s2,Ne=(3+2)N;2) 最外层和次外层能级电子数全为奇数或偶数,如Ti和Mo的外围电子构型为3d24s2和4d55s1,取Ne=2N;β是价电子路径参数。neff是由晶体结构所确定的有效价电子路径数(指价电子出现几率最大的那些路径),算法为:1) 单一晶体结构同类路径,neff等于实际路径数,如cph结构共有6接点价电子路径4个,neff =4;bcc结构共有4接点价电子路径6个,neff = 6;2) 单一晶体结构多种路径,neff等于最密排面上路径数加上其它路径折算路径数,如fcc结构共有6接点价电子路径4个和4接点路径3个,neff=4+(3/7)=4.428。
在低温下价电子处于成键状态的几率不为零,总有部分价电子不能参加导电,被视为束缚电子,这导致 的修正。另外,?T的忽略应该是有条件的,那些具有混合态的超导体的Tc不是一个确定值,可能和ΔT有关。
的修正。另外,?T的忽略应该是有条件的,那些具有混合态的超导体的Tc不是一个确定值,可能和ΔT有关。
2.2.2 计算结果及比较
由式(15)计算出的13种超导元素Tc值如表1所列(引用数据没做有效数字处理,计算值没做误差校正)。剩余的11种超导元素缺少高级电离能Ei的数据,因此没有给出计算结果。表中所使用的外围电子构型、晶体结构、摩尔原子体积、Tc的实测值来源于参考文献[17],Ei和E1值来自参考文献[18]。式(15)所使用的都是常温下数据,不需要低温参数。13种元素的计算Tc值随原子序数Z的分布趋势与实验值完全一致(见图1),仅有Nb和Sn等个别元素误差偏大。
表1 13种超导元素临界温度Tc计算值和测量值比较
Table 1 Comparison of calculated critical temperature Tc with experimental value for 13 elements
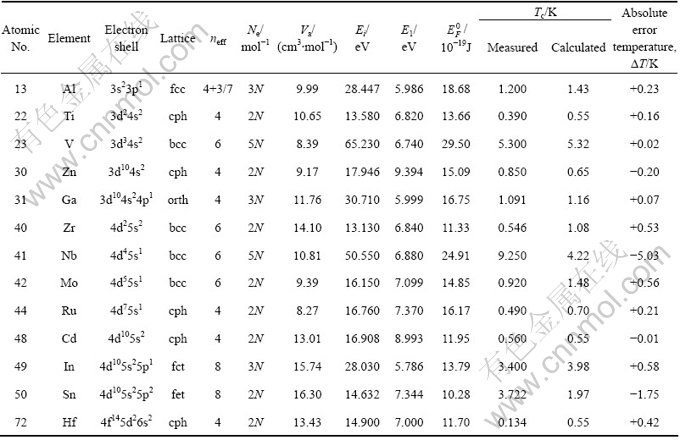
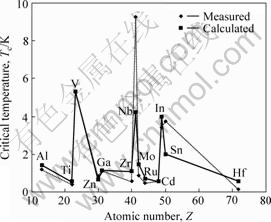
图1 Tc随原子序数Z的变化
Fig.1 Variety of calculated temperature with atomic number
Sn的Tc误差可能是因为5s2能级电子参加了导电,而在计算时按照Ne的取值规则只计算了5p2能级电子。如果Sn的5s25p2能级中有3个价电子参加导电,则Tc的计算值是4.02 K,它和实测值3.722 K仅相差 0.3 K。同理,Nb取Ne=7N计算Tc值为7.77 K,与实验值很接近。但Nb的4d45s1能级下面是填满的4p6能级,通常情况下该能级电子不参加导电。如果4p6电子参加导电,则应该是Ne=8N,以保持4p3半充满稳定结构。由于各种超导元素的E6以上高级电离能具有精确的直线关系,根据Nb的E6和E7值外推得出E8=147.40 eV,Ne=8N的计算Tc值为8.86 K,和测量值9.25 K仅相差0.39 K。
分析式(15)的有关参数和测量Tc值的数字特征,Tc计算值和测量值的误差可能来自:1) 测量Tc所用样品结晶完整性以及低温下的晶体结构,计算值为完整晶体的;2) Ne可能存在更具体的取值规则,精确计算需要采用测量Ne值;3) 从手册给出的测量Tc值数字特征看,很可能是取多次测量的平均值,但没给出测量误差。对于10?1 K数量级的Tc值来说,其测量值的波动范围是有很大影响的,如Hf等。另外,从图1显示的规律看,计算值的规律性更明显,不排除个别元素的测量Tc存在较大误差的可能性。
2.3 超导电性判据
由式(15)可知,当
(Ei?E1)≤0 (16)
Tc=0或不存在(Tc无实数值)。因此,符合式(16)的材料没有超导电性。验证该判据的是Au、Ag和Cu等单电子导电的元素,这类元素的Ei=E1,显然Tc不存在,实验已经证明了它们都不是超导元素。按照本研究提出的物理模型解释:单电子导电元素的价电子处于成键和传导双重状态且几率相等,不能忽略点状势井对其产生的散射作用。
除了10种单电子导电元素H、Li、Na、K、Rb、Cs、Fr、Cu、Ag和Au可直接用式(16)判别外,其余元素(含超导元素,但不含非导电和半导体元素及La系、Ac系、Rf、Ha、Unh)需要采用等效单电子导电元素方法进行判别(在未知元素是否超导的情况下)。根据电子能级排布规律和价电子稳定性特点,通过对各种元素的价电子结构分析,得出等效单电子导电元素的条件如下:1) 最后填充d能级且该能级只有1个电子,其余能级全充满;2) 最外面3层没有d或f能级,或只有d或f空能级,各能级全充满;3) 次外能级是d能级且有7个以上电子,次外和最外能级电子数之和是奇数;d能级有8个以上电子,次外和最外能级电子数之和等于10;最外层是d10能级;4) 次外是d能级且有5~8个电子,最外能级为s1或s2,且内层无d或f满能级。最外是半充满能级而其余能级全充满,等效单电子导电元素没有超导电性。
3 结论
1) 本征超导态理论模型不同于已有的各种超导模型,它使载流超导态和非载流超导态被分开研究,便于在正空间表述无散射(零电阻)状态。
2) 超导电性的本质是极薄的价电子层所形成的近邻离子间点状势阱,导致无散射和次近邻势阱消失,而增大价电子传导态几率。
3) 只有一个价电子参加导电的物质没有超导电性,超导材料处在单电子导电状态下将不显示超导电性。Tc随电离能Ei和E1的变化规律有可能提供一种在微弱冷却条件下测量超导临界温度Tc的新方法。具有较大的neff、 和(Ei?E1)和较小的Va的材料,即致密度和原子配位数大、价电子密度大、价电子层随温度降低而急剧减薄的材料,可能具有较高的Tc值。
和(Ei?E1)和较小的Va的材料,即致密度和原子配位数大、价电子密度大、价电子层随温度降低而急剧减薄的材料,可能具有较高的Tc值。
REFERENCES
[1] MULLER K A, BlAZEY K W, BEDNORZ J G, TAKASHIGE M. Superconducting glassy state in high-Tc oxides[J]. Physica, 1987, B+C 148: 149?154.
[2] ANDERSON P W. The resonating valence bond statein La2CuO4 and superconduction[J]. Science, 1987, 235: 1196?1198.
[3] NAGAMATSU J, NAKAGAWAN N. Superconductivity at 39 K in magnesium diboride[J]. Nature, 2001, 410(3): 63?64.
[4] JEROMED, BECHGAARD K. Condensed-matter physics: superconducting plastic[J]. Nature, 2001, 410(3): 162-163.
[5] SCH?N J H, KLOC C, BATLOGG B. High-temperature superconductivity in lattice-expanded C60[J]. Science, 2001, 293: 2432?2434.
[6] FOMINOV Y V, GOLUBOV A A. Density of states in d –wave superconductors of finite size[J]. Phys Rev, 2004, B70: 212513?212515.
[7] 刘心宇, 黄 勇, 曾中明. MgB2超导电性研究进展[J]. 材料科学与工程学报, 2003, 21(1): 104?108.
LIU Xin-yu, HUANG Yong, ZENG Zhong-ming. Research and progress in magnesium diboride superconductor[J]. Journal Materials Science and Engineering, 2003, 21(1): 104?108.
[8] 李燕峰, 徐 慧, 宋招权, 夏庆林, 程仕平. Zn掺杂对MgB2电子结构及超导转变温度的影响[J]. 中南大学学报: 自然科学版, 2006, 37(5): 925?931.
LI Yan-feng, XU Hui, SONG Zhao-quan, XIA Qing-lin, CHENG Shi-ping. The effect of Zn doping on the electronic structure and superconductivity temperature of MgB2[J]. Journal of Central South University: Science and Technology, 2006, 37(5): 925?931.
[9] 禹争光, 马衍伟, 王栋梁, 张现平, 高召顺, WATANABE K, 黄伟文. 高性能长线材制备及性能表征[J]. 物理学报, 2007, 56(11): 6680?6683.
YU Zheng-guang, MA Yan-wei, WANG Dong-liang, ZHANG Xian-ping, GAO Zhao-shun, WATANABE K, HUANG Wei-wen. Fabrication and characteristics of long MgB2 wire with high superconducting properties[J]. Acta Physica Sinica, 2007, 56(11): 6680?6683.
[10] ZOU Zhuang-hui, YU Xiao-ming, ZHANG Bing-sen, QI Yang. Analysis of temperature dependence of phases and surface morphology of Bi2Sr2Cax?1CuxOy thin films using reactive CO-deposition method[J]. Acta Metall Sin (Eng Lett), 2007, 20(3): 199?204.
[11] 易汉平, 张劲松, 刘 庆, 韩征和. 实用Bi系超导带材[J]. 中国有色金属学报, 2004, 14(S1): 341?346.
YI Han-ping, ZHANG Jin-song, LIU Qing, HAN Zheng-he. Applied high temperature superconductivity band of Bi alloy[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(S1): 341?346.
[12] 叶 帅, 索红莉, 刘 敏, 赵 跃, 何 东, 祝永华, 马灵姬, 周美玲. 改进YBCO薄膜高场性能的研究进展[J]. 低温物理学报, 2008, 30(1): 23?28.
YE Shuai, SUO Hong-li, LIU Min, ZHAO Yue, HE Dong, ZHU Yong-hua, MA Ling-ji, ZHOU Mei-ling. Recent progress on enhancing field-properties of YBCO coated conductors[J]. Chinese Journal of Low Temperature Physics, 2008, 30(1): 23?28.
[13] BARDEEN J, COOPER L N, SCHRIEFFER J R. Theory of superconductivity[J]. Phys Rev, 1957, 108: 1175?1181.
[14] MILLIS A J, MONIEN H, PINES D. Phenomenological model of nuclear relaxation in the normal state of YBa2Cu3O7[J]. Phys Rev, 1990, B42: 167?172.
[15] SCHREFFER J R, WEN X G, ZHANG S C. Dynamic spin fluctuations and the bag mechanism of high-Tc superconductivity[J]. Phys Rev, 1989, B39: 11663?11679.
[16] BLAKEMORE J S. Solid state physics[M]. Cambridge: Cambridge University Press, 1985: 178?182.
[17] BERGER L I, ROBERTS B W. CRC handbook of chemistry and physics[M]. 82nd ed. Florida: CRC Press, 2001: 12?65.
[18] LIDE D R. Handbook of chemistry and physics[M]. 71st ed. Florida: CRC Press, 1990?1991.
收稿日期:2007-01-17;修订日期:2008-03-19
通讯作者:祁 阳,教授,博士;电话/传真:024-83684950;E-mail: qiyang@imp.neu.edu.cn
(编辑 李艳红)