Trans. Nonferrous Met. Soc. China 26(2016) 2462-2468

Database-oriented storage based on LMDB and linear octree for massive block model

Lin BI, Hui ZHAO, Ming-tao JIA

School of Resources and Safety Engineering, Central South University, Changsha 410083, China

Received 14 January 2016; accepted 12 June 2016

Abstract: Data organization requires high efficiency for large amount of data applied in the digital mine system. A new method of storing massive data of block model is proposed to meet the characteristics of the database, including ACID-compliant, concurrency support, data sharing, and efficient access. Each block model is organized by linear octree, stored in LMDB (lightning memory-mapped database). Geological attribute can be queried at any point of 3D space by comparison algorithm of location code and conversion algorithm from address code of geometry space to location code of storage. The performance and robustness of querying geological attribute at 3D spatial region are enhanced greatly by the transformation from 3D to 2D and the method of 2D grid scanning to screen the inner and outer points. Experimental results showed that this method can access the massive data of block model, meeting the database characteristics. The method with LMDB is at least 3 times faster than that with etree, especially when it is used to read. In addition, the larger the amount of data is processed, the more efficient the method would be.

Key words: block model; linear octree; lightning memory-mapped database; mass data access; digital mine; etree

1 Introduction

3D geological modeling is composed of geological structure modeling and attribute modeling [1], which is the basis for digital mine as well as intelligent mine [2]. The structure model, namely surface model, can well describe the space shape of complex ore body, but the attributes of any point inside the model need to be expressed and carried by attribute model because of inhomogeneity of geological grade. The attribute modeling of geological body usually means discreting the geological body into a mesh of voxels [3] which can be tetrahedral, hexahedral, prism, polyhedral, etc. The attribute model composed of hexahedral voxels is generally called block model. The majority mining softwares (Vulcan, Data mine, Surpac, Mine Sight, Micro mine, Dimine, QuantyMine, 3DMine, etc.) use block model as the attribute model. The data quantity of block model is huge, even massive. In the application of mining software, the following requirements are necessary for the block model: 1) Supporting concurrency and sharing for massive data of geological attributes, in which it requires that the storage method meets the characteristics of the database: ACID- compliant and concurrency support; 2) The data access should be fast enough, especially the attribute query based on any spatial point and any spatial 3D area. In this work, thanks to the linear octree and LMDB, the efficient storage of massive data of block model was realized to meet the characteristics of the database by making comparative analysis with the implementation based on etree. Meanwhile, the screening algorithm, by means of 2D grid scanning, improved the efficiency and robustness of the regional query greatly.

2 Expression of block model

2.1 Way of expression

Based on the geological structure model, the block model focused on 3D rasterization. As shown in Fig. 1 (using 2D to express for convenience), further subdivision of the boundary of the ore body is required to meet the accuracy requirement. The block model was usually expressed with octree. As a result, complex geological body with complex boundary can be accurately interpreted [4,5]. The octree can not only represent accurately the features of complex geological body boundary, but also take a great significance in which the storage space could become smaller, generally only 10%-30% of 3D grid data [6]. In addition, the hierarchical structure of octree can increase the speed of retrieval, subdivision, merging and so on.

Owing to the lack in regularity as the grid model, the octree model does not act as well as the grid model in querying. In consideration of the requirements of massive data, this paper adopts the encoding of linear octree in which address code is usually represented by Morton code [7]. The Morton code maps a point on the d-dimensional space to an integer, which can be realized by exchanging the bits of Cartesian coordinate.

Fig. 1 Discrete geological bodies

2.2 Location code

Figure 2 shows that a domain is a Cartesian coordinate space that consists of a uniform grid of 2ⁿ×2ⁿ indivisible units. The level 0 at the root covers the entire domain, and each sub-node ratio increases 1 level than its parent. The address of each block is determined by the Cartesian coordinate (x, y, z) of its lower left corner and its level. For example, b is (0, 0, 0, 1), c is (8, 0, 0, 1), and j is (6, 10, 0, 3).

The higher the level of the octree is, the more precise the block model can be subdivided; thus larger storage space will be required. In order to facilitate realization of location code comparison function, considering efficiency, accuracy and other factors, location codes are represented by 13 bytes. Each dimension of Cartesian coordinate is represented by 4 bytes, 12 bytes for the three-dimensional, 1 byte for the node type (leaf or internal node) and level. Obviously, the location of 13 bytes can define up to 32 levels (0-31) of the octree. The node at 0 level is the largest one covering the entire address space, while the smallest node is at the 31st level, whose size is one basic unit. The size of the node at k level is 2^(31-k) basic units. A block model with 13 bytes as the location code is sufficient to express any scale of mine and meets the accuracy requirements. For example, for a mine of 1000 km, the basic unit length can be 0.5 mm.

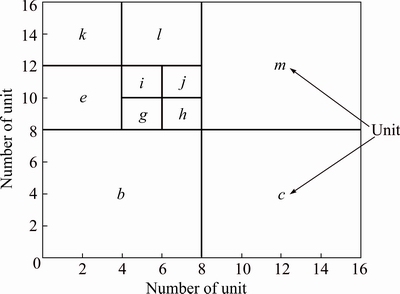
Fig. 2 Octree area descriptions

3 Storage of block model

As mentioned above, the block model is represented by linear octree. The linear octree is a technique for assigning unique addresses to octants [8,9]. It allows octants to be located quickly, without actually storing the topological structure of the octree on disk. The linear octree only save and deal with leaf nodes, and the leaf node consists of two parts: the location code and attribute data. This feature is suitable for the key-value database to store data. The key-value database is one of the important types of NoSQL [10] database. NoSQL database is to solve the challenges of large-scale data collection of multiple data types, especially for the big data application problems. Both etree [11] and LMDB [12] are key-value storage databases. Their basic idea is to represent all input and output datasets stored on disk, so as to support the massive data storage. Based on these two different techniques, we designed two storage solutions for block model, and made some comparative analysis, then found the most appropriate solution.

3.1 Storage based on etree

The etree is a database-oriented method for large out-of-core octree mesh generation. It is widely used in large data access [13-15]. The main idea is to map an octree to a database structure and perform all octree operations by querying and updating the database. The etree only achieves the storage of massive data, but does not meet many features of the database, such as ACID, transaction and concurrency.

Figure 3 shows the structure of etree, and it is based on B⁺ tree. B⁺ tree has been used in database systems for decades, and is well-suited for efficient data storage and retrieval [16]. Etree stores a series of fixed length records that contain location codes and sorted by location code. Each record, indexed by B⁺ tree, consists of two parts: location code and attributes.

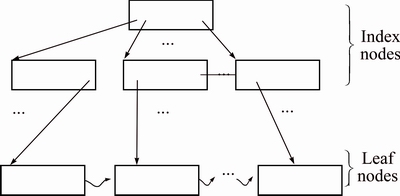
Fig. 3 Etree structure of block model

There are two types of nodes in an etree: the leaf nodes and the index nodes. The leaf nodes contain data to be searched. The structure of a leaf node is an array of records with the form , shown in Fig. 4(a). The index nodes contain routing information to guide the search for a given key value. The structure of an index node is an array of pairs , as shown in Fig. 4(b). These nodes are mapped to disk pages, so the pointers are actually disk page number.

The block model data are stored in the disk file by B⁺ tree index, sorted by location code that can solve the bottleneck problem of massive data management and fast access.

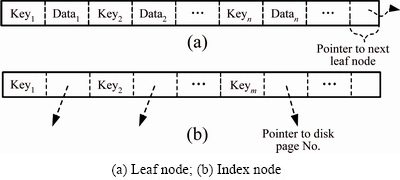
Fig. 4 B⁺tree node

3.2 Storage based on LMDB

Lightning memory-mapped database (LMDB) is an embedded key-value data store developed by Symas, written in C [12,17]. It was developed for the OpenLDA Project with the aim of replacing Berkeley DB (BDB [18]) as its storage backend, and improved from the following aspects:

1) LMDB stores data in a copy-on-write B⁺ tree. Figure 5 illustrated this approach. By implementing a copy-on-write variant of B⁺ trees, LMDB is able to provide a form of multi-version concurrency control (MVCC), allowing write- and read-transactions to operate concurrently.

2) One of the initial goals of the LMDB project is to create a system where no buffer and cache configuration and management are necessary. LMDB achieves this by using the operation system’s memory-mapping capability to access on-disk data, leaving caching and buffer- management up to the file system and OS instead of LMDB itself. For this approach to be viable, the memory address space of the operating system that LMDB is running on must be large enough to contain the expected data volume. For 32 bit systems, this sets a hard limit on 4 GB. In recent years, 64 bit systems have became more common, which ups the limit to between hundreds of terabytes and multiple exabytes [17].

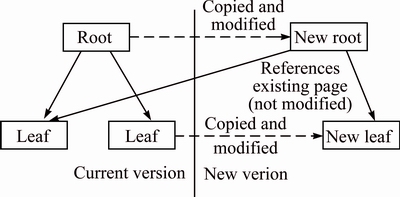
Fig. 5 Copy-on-write B⁺ tree operations

Based on the above technology, the LMDB has the following major features: Key/value store implemented using B⁺ trees: ordered-map interface with sorted keys; support for range lookups; fully transactional; concurrency support, and so on.

More advanced features include support for storage of multiple databases in a single file, nested transactions, and storage of multiple values for a single key. So LMDB is very suitable for the storage of massive block model, and meets the features of database.

Unlike etree’s node, LMDB has only one node type illustrated in Fig. 6. First, two unsigned shorts are stored, which together denote the size of the key-value pair’s value (for leaf-pages) or the page-number the node points to (for branch-page). Next is a field used to store additional information about the node, then the length of the key-value pair’s key. Finally, there comes a variable- length array used to store the actual key- and value-data.

Fig. 6 Format of single LMDB node

By using this kind of structure, LMDB is able to quickly locate where a key-value pair is stored in a page, as well as to add a new key-value pair without having to move around a large amount of data.

4 Query and retrieval

4.1 Comparison of location code

Location code is designed to establish the index and to access the node data quickly and accurately, so the location code comparison algorithm is very important. For the purpose of comparison, we treat the byte sequence as a large positive integer. The length (13-byte) of the location code byte sequence may be longer than any integer data type. To enable the comparison between two conceptually large integers, we perform a integer- wise comparison, starting from the most significant integer of the sequence down to the least significant integer, as shown in Fig. 7(a), integer pair 1,I₂> compared first, then 1,J₂> compared, then 1,K₂> compared. The comparison function returns the relationship between two levels from the 13th byte if the three integers are equal. Using this comparison function to sort the octants of an octree in increasing locational code order, the ordering of octants is exactly the same as that processed by the preorder traversal of the octree. By preorder traversal, we mean visiting the root, and then recursively visiting its children in directional code order, as shown in Fig. 7(b). Figure 7(c) shows nodes in ascending order by location code.

Given these observations, we can get the characteristics of location code comparison algorithm: 1) The location code of root is the smallest; 2) The location code of subtree’s root is less than location code of any child nodes; 3) If the location node of A is less than location node of B, the location code of any sub node of A is less than location code of any sub node of B. Given these features, we can use the locational code of the query unit as a search key and ask the database to return the octant whose locational code is the maximum among all the locational codes that are less than the search key. Thus, we are guaranteed to locate the leaf octant only that the query pixel is enclosed in the leaf octant.

Both etree and LMDB can customize key- comparator function determining ordering among different keys. Etree has a handler to application comparison function (etree_compar_t *compar), and LMDB has an API (mdb_set_compar) to set the client- specified key-comparator function.

4.2 Attribute query for any point in space

The location code corresponding to the point must be calculated from the Cartesian coordinate when querying the attribute at one point of space. Assuming that the Cartesian coordinate of the point is (x, y, z), the coordinate of lower left corner of the block model is (x_origin, y_origin, z_origin), and the range of the block model is (x_len, y_len, z_len), the address (a_x, a_y, a_z) of the point can be calculated from the following formula:

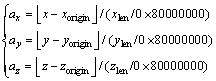          (1)

As mentioned above, location code is composed of address code and level, but it is difficult to get level of points. Luckily, according to the characteristics 2) of location code comparison algorithm, applications can query arbitrary points without any knowledge of the 4 structure of the octree. That is why we can use the maximum level (31) as the level to compose the location code.

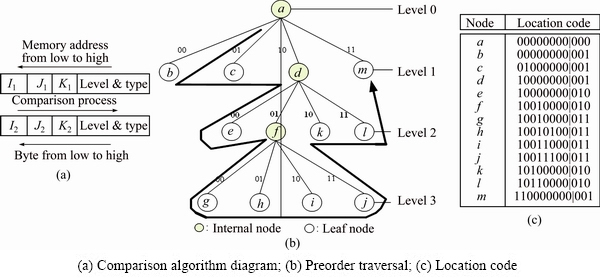
Fig. 7 Preorder traversal of octree

4.3 Atribute query for arbitrary 3D region

In practical application, geological attribute within 3D region (polyhedral) often wants to be queried, for example, the reserves of ore body, the average grade of stope, the metal amount of stope, the dilution and loss of mining, the byproduct in tunneling, optimization in open-pit [19], and so on. These problems can be attributed to the problem of “query for polyhedral from block model”. Luckily, the problem can be translated into “query for point” problem by polyhedron rasterization that polyhedrons are discretized into voxels and query by the centers of voxels.

As mentioned above, in condition that the correct attribute can be hit at any point, the efficiency and robustness of the polyhedron rasterization are important factors. The important technology of discretization is the fast and accurate judgment of the relation between the points and the polyhedron. BI et al [4] optimized the ray method to judge the internal and external relations with the OBB tree and node intersection test, and the performance has improved, but the robustness is poor. JING et al [20] improve the robustness with Feito- Torres method, but performance has declined. LI et al [21] used flood-fill to to reduce the time complexity to O(n); however, a large number of triangle intersection operations need to be carried out. For solving those problems, the decision problem of point in polyhedron is transformed into a point in polygon in which the 3D problem is transformed into 2D problems. As a result, the problem is greatly simplified. The ray method is a common method to judge the relationship between the point and polygon [22]. Based on the idea of ray method, we propose a new method, 2D grid scanning to screen the inner or outer points. The process is as follows:

1) Rasterize the target of 3D space based on the unit size of block model and create 3D grid;

2) Cut the polyhedron with plane through the center of each layer and create 2D contour lines;

3) Screen the inner or outer of pixels for every layer by the raster scan method.

Among them, the raster scanning method is very important. Assuming the row, column, layer of the 3D grid is N (N=2ⁱ, i is a non-zero positive integer), its process is as follows:

1) Initialize all elements “outside” mark;

2) Produce a ray R_xj from x=x_j parallel to the y-axis; x_j is x-component of coordinate of column j,

3) Compare x_j and x-component (x₁, x₂) of all of the end points of contour lines on k layer. There is an intersection between line segment and R_xj, if x₁j2 (without loss of generality, assuming x₁2);

4) Calculate the y-component value of the intersection using formula (2):

y=y₁+(y₂-y₁)×((x-x₁)/(x₂-x₁))                   (2)

Find all the intersection and calculate all the y-component values sorted in ascending;

5) Make “intersection pairs” for the y-component values as (y₀, y₁), (y₂, y₃), …, (y_c-2, y_c-1): (y_i, i=0, 1, …, c-1) (c is number of intersections));

6) Set “internal” flag for the elements which center is located between one “intersection pairs”;

7) Execute (2) until all layers are processed.

As can be seen from the above, the algorithm does not have to calculate the intersection, just make a simple judgment. As a result, the performance and robustness of the algorithm are improved greatly.

5 Experiments and analysis

The storage method was realized by VC++, running on windows7 64 bits OS, CPU was Intel (R) Core (TM) i5-4750 @ 3.20 GHZ CPU, 4G memory, hard drives are HDD, 7200 RPM. The scope of one mining was (3450.0 m, 3862.0 m, 812.0 m), its structure model was shown in Fig. 8(a) and its block model was shown in Fig. 8(c). The query region was shown in Fig. 8(b), and its size was (1361.0 m, 1462.0 m, 715.0 m), and its block model was shown in Fig. 8(d). A comparative analysis was carried out between LMDB and etree according to different three scenarios: the same fields but different number of blocks, the same number of blocks but different fields and different key-comparator functions.

5.1 Experiment 1: Same fields but different numbers of blocks

The fields remained unchanged, 3 doubles and one string of 32 bytes, as well as the number of blocks was increased by 8 times (the level of octree were incremented by 1). The two storage methods was compared by analyzing the data size, consuming time to create, consuming time to query, and so on. The results were shown in Table 1.

As can be seen, LMDB occupies more storage space than etree. The reason is that LMDB can save variable-length records, and needs to hold the length of key and value. Nonetheless, the feature of variable- length key and variable-length value is lamb’s advantage that can be used to store data collection of multiple data types. LMDB is much faster than etree, and the more the number of blocks is, the more obvious the tendency is. The main reason is that the entire database of LMDB is mapped into virtual memory and all data fetched are performed via direct access to the mapped memory instead of through intermediate buffers and copies. In addition, the screening is time-used less and does not increase dramatically as the number of blocks increases because of the raster scanning method.

5.2 Experiment 2: Same number of blocks but different fields

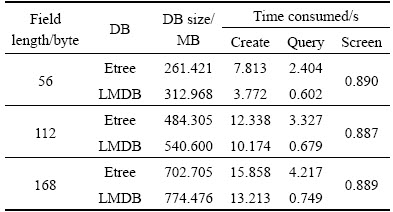
In this experiment, the fields of different lengths (56, 112, 168 bytes) were adopted and the number of blocks model remained unchanged. We performed the same comparative analysis as above. The results are shown in Table 2.

The results showed that the time-consuming of reading and writing increased with the increase of the amount of data. The time-consuming of screening remained about the same because of screening is only related to number of block to be queried.

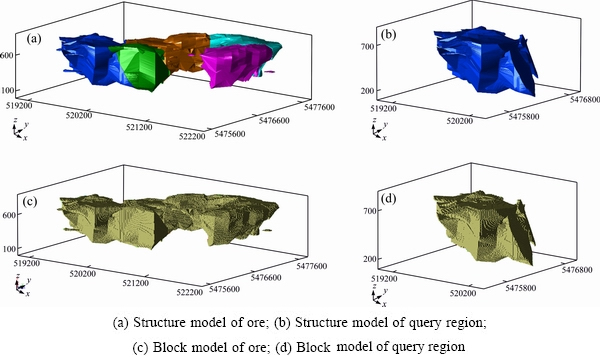
Fig. 8 Mining and query region

Table 1 Results of same fields but different numbers of blocks

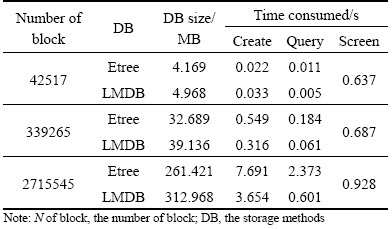
Table 2 Results of same number of blocks but different fields

5.3 Experiment 3: Different key-comparator functions

In this experiment, both the length of the fields and the number of blocks remain unchanged, but the key-comparator function is different, one is integer-wise comparison proposed previously, one is “memcmp” which is a function comparing the first n characters of two object. The results are shown in Table 3.

It is obvious that the key-comparator function proposed in this work is better than memcmp function. The reason using this comparison function to sort the octants of an octree in increasing location code and the order of octants is exactly the same as that processed by the preorder traversal of the octree, and the preorder traversal of the octree can track “z” pattern (z-order) [23,24], as shown in Fig. 9, and z curve has a good space accumulation [25].

Table 3 Result of different key-comparator functions

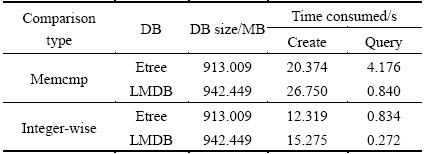
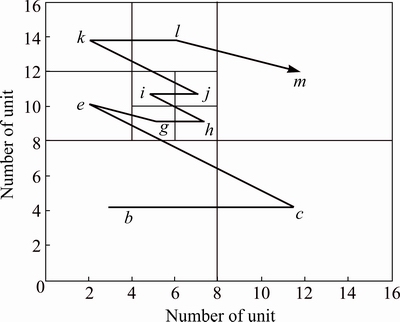
Fig. 9 Spatial aggregation of z-curve

6 Conclusions

1) Owing to usage of memory-map and copy-on- write B⁺ tree, LMDB is superior to etree in storage of massive data of block model.

2) Combining the advantages of linear octree and LMDB, the new method is a better way to realize the storage of massive data of geological attribute on 64 bit systems, and meets the characteristics of the database.

3) The performance and robustness of querying from block model are improved greatly by transforming from 3D to 2D and 2D grid scanning.

References

[1] HUA Wei-hua. Rapid modeling and quantitative analysis of the complex geological bodies with multi-constraint [D]. Wuhan: China University of Geosciences, 2010. (in Chinese)

[2] JIN B X, FANG Y M, SONG W W. 3D visualization model and key techniques for digital mine [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(S3): s748-s752.

[3] WU Jiang-bin, ZHU He-hua. 3D ten model of strata and its realization based on delaunay triangulation [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4581-4587.

[4] BI Lin, WANG Li-guan, CHEN Jian-hong. Study of octree-based block model of complex geological bodies [J]. China University of Mining and Technology Journal, 2008, 37(4): 532-537.

[5] CHERNYSHENKO A Y, OLSHANSKII M A. An adaptive octree finite element method for PDEs posed on surfaces [J]. Computer Methods in Applied Mechanics and Engineering, 2015, 291:146-172.

[6] HAN Guo-jian, GUO Da-zhi, JIN Xue-lin. Storage and indexing of orebody information using octrees [J]. Acta Geodaetica et Cartographica Sinica, 1992, 21(1):13-17.

[7] MORTON G M. A computer oriented geodetic data base and a new technique in file sequencing [M]. New York: International Business Machines Company, 1966.

[8] GARGANTINI I. An effective way to represent quadtrees [J]. Communications of the ACM, 1982, 25(12): 905-910.

[9] GARGANTINI I. Linear octrees for fast processing of three- dimensional objects [J]. Computer Graphics and Image Processing. 1982, 20(4): 365-374.

[10] HAN J, HAIHONG E, LE G. Survey on NoSQL database [C]//Proceedings of 6th International Conference on Pervasive Computing and Applications (ICPCA), 2011. Albuquerque: IEEE, 2011: 363-366.

[11] TU T, O’HALLARON D R,  J C. Etree: A database-oriented method for generating large octree meshes [J]. Engineering with Computers, 2004, 20(2): 117-28.

[12] CHU H. Mdb: A memory-mapped database and backend for openldap [J]. LDAP’11. 2011.

[13] KIM E, BIELAK J, GHATTAS O. Large-scale northridge earthquake simulation using octree-based multiresolution mesh method [C]//Proceedings of the 16th ASCE Engineering Mechanics Conference. Seattle: ASCE, 2003: 1-6.

[14] TU T. A scalable database approach to computing delaunay triangulations [D]. Pittsburgh: Carnegie Mellon University, 2008.

[15] GILL D, MAECHLING P J, JORDAN T H. UCVM: An open source framework for 3D velocity model research [C]//AGU Fall Meeting Abstracts, San Fracisco: AGU, 2013: 1612.

[16] COMER D. Ubiquitous B-tree [J]. ACM Computing Surveys (CSUR), 1979, 11(2): 121-37.

[17] CHU H. LIFE. After berkeley DB: OpenLDAP's memory-mapped database [EB/OL]. [2012]. http://symas. com/mdb/20120829- LinuxCon-MDB-txt. pdf.

[18] YADAVA H. The berkeley DB book [M]. New York: Apress, 2007.

[19] GU X W, WANG Q, SHU G E. Dynamic phase-mining optimization in open-pit metal mines [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(10): 1974-1980.

[20] JING Yong-bin, WANG Li-guan, BI Lin. Robust creation of block model from complex orebody model [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(2): 97-100.

[21] LI Nan, WU Xin-cai, XIAO Ke-yan. A fast method for constructing complex orebody block model of the algorithm [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(3): 34-37.

[22] TAYLOR G. Point in polygon test [J]. Survey Review, 1994, 32(254): 479-84.

[23] ORENSTEIN J A, MERRETT T H. A class of data structures for associative searching [C]//Proceedings of the 3rd ACM SIGACT-SIGMOD symposium on Principles of Database Systems. Waterloo: ACM, 1984: 181-190.

[24] ORENSTEIN J A. Spatial query processing in an object-oriented database system [J]. ACM Sigmod Record, 1986, 15(2): 326-336.

[25] FALOUTSOS C, ROSEMAN S. Fractals for secondary key retrieval [C]//Proceedings of the Eighth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems. ACM, 1989: 247-252.

面向数据库特征的基于LMDB与线性八叉树海量块段模型存储技术

毕 林，赵 辉，贾明涛

中南大学 资源与安全工程学院，长沙 410083

摘  要：为满足数字矿山系统应用中对海量数据高效存取的技术要求，提出一种块段模型海量数据存储新方法。该存储技术满足数据库的特点：ACID兼容、并发支持、数据共享及高效访问；采用线性八叉树的方法组织块段模型，并存将其储于LMDB(快速内存映射数据库)中；通过定位码比较算法及从几何空间地址码到存储空间定位码的转换算法，可高效地对三维空间任意点的地质属性进行查询；采用三维到二维的转换及内外点二维网格扫描筛选法，使地质属性查询的三维问题转化为二维问题，其性能和鲁棒性得到显著提高。实验结果表明，这种方法能够高效存取块段模型海量数据，并满足数据库的特点；相比于采用etree方法，采用LMDB方法至少快3倍，特别是在读取数据时效率更高，且数据量越大，效果越明显。

关键词：块段模型；线性八叉树；快速内存映射数据库(LMDB)；海量数据访问；数字矿山；etree

(Edited by Yun-bin HE)

Foundation item: Projects (41572317, 51374242) supported by the National Natural Science Foundation of China; Project (2015CX005) supported by the Innovation Driven Plan of Central South University, China

Corresponding author: Lin BI; Tel: +86-731-88877665; E-mail: mr.bilin@163.com

DOI: 10.1016/S1003-6326(16)64377-7