DOI： 10.11817/j.issn.1672-7207.2021.03.011
锈蚀栓钉钢-混凝土组合梁的疲劳寿命预测模型
匡亚川1，陶莉1，贺宇豪2
(1. 中南大学 土木工程学院，湖南 长沙，410075；
2. 长沙高新控股集团，湖南 长沙，410000)
摘要：采用有限元分析软件ANSYS和理论公式相结合的方法，提出一种预测锈蚀栓钉钢-混凝土组合梁疲劳寿命的模型。根据钢-混凝土组合梁在实际试验中发生疲劳破坏的原理，提出组合梁在疲劳加载过程中栓钉依次退出工作的假设，同时把栓钉疲劳寿命预测模型和栓钉剩余承载力计算公式与数值分析相结合，综合考虑疲劳加载幅、疲劳加载上限、栓钉极限承载力、栓钉直径以及栓钉初始缺陷等因素对组合梁疲劳寿命的影响，计算分析组合梁的疲劳寿命。首先预测未锈蚀栓钉钢-混凝土组合梁的疲劳寿命，在验证模型的有效性基础上，综合考虑锈蚀率对栓钉极限强度、屈服强度、弹性模量、截面直径和本构关系等因素的影响，修正组合梁有限元分析模型，并结合锈蚀栓钉的疲劳寿命预测模型，对锈蚀栓钉钢-混凝土组合梁的疲劳寿命进行模拟计算。研究结果表明：采用本文提出的模型预测组合梁试件FSCB-4和FSCB-5的疲劳寿命，计算结果与试验结果的相对误差分别为12.30%和6.95%，较利用传统S-N曲线的分析方法具有更高的精度，与试验值更吻合；栓钉的锈蚀对钢-混凝土组合梁的疲劳寿命影响较大，当栓钉的锈蚀率分别为5%，10%，15%和20%时，组合梁的疲劳寿命分别下降11.51%，25.27%，48.08%和79.65%。
关键词：锈蚀栓钉；钢-混凝土组合梁；疲劳寿命；数值分析；锈蚀率
中图分类号：TU398 文献标志码：A 开放科学(资源服务)标识码(OSID)：
文章编号：1672-7207（2021）03-0770-09
Fatigue life prediction model of corroded studded steel-concrete composite beam
KUANG Yachuan1, TAO Li1, HE Yuhao2
(1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. Changsha High-tech Holdings Group, Changsha 410000, China)
Abstract: A model for predicting the fatigue life of steel-concrete composite beams with corroded studs was proposed by combining the finite element analysis software ANSYS and theoretical formulas. According to the principle of fatigue failure of steel-concrete composite beams in actual tests, it was proposed that the studs of composite beams would withdraw from work in the process of fatigue loading. At the same time, the stud fatigue life prediction model and the calculation formula of the stud residual bearing capacity were combined with numerical analysis to calculate the fatigue life of composite beams considering fatigue loading amplitude, upper limit of fatigue loading, ultimate bearing capacity of the stud, diameter of the stud, bolt stud nail initial defects on the fatigue life of composite beams. Firstly, the fatigue life of the steel-concrete composite beam with uncorroded studs was predicted. On the basis of verifying the validity of the model, the finite element analysis model of the composite beam was modified considering the influence of the corrosion rate on the ultimate strength, yield strength, elastic modulus, section diameter and constitutive relationship of the studs. Combined with the fatigue life prediction model of corroded studs, the fatigue life of steel-concrete composite beam with corroded studs was predicted. The results show that the fatigue life prediction model proposed in this paper is used to predict the fatigue life of composite beam specimens FSCB-4 and FSCB-5, and the error between the calculated results and the test results are 12.3% and 6.95% respectively. Compared with the traditional S-N curve analysis method, it has higher accuracy and is more consistent with the test value. The corrosion of studs has a great influence on the fatigue life of steel-concrete composite beams. When the corrosion rates of studs are 5%, 10%, 15% and 20%, the fatigue life of composite beams decreases by 11.51%, 25.27%, 48.08% and 79.65% respectively.
Key words: corroded studs; steel-concrete composite beams; fatigue life; numerical analysis; corrosion rates
钢-混凝土组合梁桥兼有钢桥和混凝土桥各自在经济性和施工性等方面的优点，是一种高性能梁桥结构形式，在综合效益上具有强大竞争力，具有广阔的应用和发展前景[1-3]。我国组合梁桥具有服役环境复杂、行车密度高和载荷大等特点，疲劳损伤演化和累积问题突出。钢-混凝土组合梁桥在服役期内受车辆荷载和环境侵蚀等多种因素共同作用，导致钢材的疲劳寿命明显下降[4-6]。目前关于组合梁桥疲劳性能的研究成果未考虑车辆荷载与环境耦合效应的影响，国内外学者对于荷载与环境耦合作用下组合梁桥的劣化机理认识不足，仅仅了解到环境与荷载的耦合作用将加速耐久性能、疲劳性能和承载能力的劣化过程[7-11]。因此，加快该领域的科学研究，为组合梁桥的设计与建造提供理论依据，对确保组合梁桥的安全运营，促进组合梁桥的应用与发展具有重大的现实意义。
断裂力学是研究具有初始缺陷的材料和结构疲劳强度的有力工具，其有效性已得到国内外疲劳界学者的公认。断裂力学能够定量计入初始缺陷对材料疲劳寿命的影响，以裂纹尺寸和裂纹扩展速率作为结构损伤的判据，判定其疲劳寿命[12-13]。本文从钢-混凝土组合梁在实际试验中发生疲劳破坏的原理和栓钉的腐蚀疲劳裂纹扩展机理出发，结合栓钉疲劳寿命预测模型，采用ANSYS有限元分析软件，分析锈蚀栓钉钢-混凝土组合梁的疲劳性能。
1 钢-混凝土组合梁疲劳破坏机理
钢-混凝土组合梁发生疲劳破坏时，主要有以下2种破坏模式：
1) 下部钢梁翼缘由于拉应力过大而发生受拉破坏；
2) 连接混凝土板和钢梁的栓钉连接件发生疲劳断裂[14]。
钢梁翼缘的疲劳破坏为脆性破坏，从裂纹出现到组合梁整体破坏，整个过程十分迅速。故在设计钢-混凝土组合梁时，通过控制栓钉应力与钢梁翼缘应力的比值，避免钢梁翼缘发生疲劳破坏。在疲劳荷载作用下，钢-混凝土组合梁中的栓钉通常在结合面处发生多根栓钉疲劳断裂。当第1根栓钉断裂后，组合梁将会发生应力重新分布，界面处的剪力将由剩余的栓钉继续协同承担，这时剩余栓钉所承担的应力将会增大，组合梁整体仍然能够继续承受疲劳荷载。但随着有效栓钉的数量逐渐减少，组合梁的整体抗剪强度将会下降，导致抗剪承载能力不足，界面滑移增大，最后钢-混凝土组合梁发生疲劳破坏。由于组合梁中的栓钉不是同时发生疲劳断裂，而是存在次序性，故组合梁在疲劳荷载作用下的整体破坏具有一定延性。
2 钢-混凝土组合梁疲劳性能及寿命预测
2.1 钢-混凝土组合梁相关疲劳试验
文献[15]进行了7个缩尺钢-混凝土组合梁的疲劳性能试验。为了将本文的模拟计算结果与文献[16]中的模拟计算结果进行对比分析，选取的构件编号与文献[16]一致，即选取编号为FSCB-0，FSCB-4和FSCB-5的组合梁构件，组合梁的尺寸如图1所示。混凝土板与钢梁通过30根直径为16 mm、高度为90 mm的栓钉连接(采用不完全剪力连接)，以保证二者的协同作用，混凝土强度等级为C35，栓钉的极限强度为509 MPa。试件中钢材的屈服强度为362.89 MPa，极限强度为458.03 MPa。试件FSCB-0进行静载试验，试件FSCB-4和FSCB-5进行疲劳试验，疲劳试验的试验结果如表1所示。
图1 组合梁试件构造尺寸
Fig. 1 Structural dimensions of composite beam specimens
表1 疲劳试验结果
Table 1 Fatigue test results
2.2 栓钉疲劳寿命预测模型
在钢-混凝土组合梁中，栓钉主要承受剪应力，基于断裂力学理论，以Paris公式为基础，推导出钢-混凝土组合梁中栓钉的疲劳寿命预测模型为[17]：
(1)
式中：
为组合梁的疲劳寿命；
为疲劳加载应力幅；Y为材料相关常数；
为栓钉初始裂纹深度；C和n为Paris参数，可通过试验确定；
为栓钉发生疲劳破坏时的临界裂纹长度，可按式(2)进行计算。
(2)
式中：
为栓钉直径；
为栓钉截面面积；
为栓钉的极限抗剪强度；
为栓钉发生剪切破坏时的疲劳荷载上限。
对式(1)进行简化，令C′=
，M=
，则有：
(3)
根据文献[18]，取初始裂纹深度
mm。结合已有试验数据，利用Matlab软件中的非线性拟合命令lsqcurvefit对式(3)中的关键参数
和M进行拟合，拟合得到＝6.65×10-16，M＝-1.05[17]。将参数，M和式(2)代入式(3)，即可得到简化后的栓钉疲劳寿命预测模型：
(4)
由式(1)可知，在组合梁中，随着疲劳荷载循环次数增加，栓钉的疲劳裂纹将会不断扩展，栓钉的有效面积逐渐减小，而栓钉承受的应力逐渐变大，当荷载循环次数达到一定次数时，承受最大应力的栓钉首先发生破坏。当加载次数达到栓钉的疲劳寿命时，疲劳裂纹发展到临界裂纹深度，栓钉的承载力迅速下降，很快发生疲劳断裂破坏，可由式(4)计算出该栓钉的疲劳寿命。栓钉经过N次循环荷载后，若疲劳裂纹尚未发展至其临界裂纹深度，栓钉仍能继续承受疲劳荷载，但栓钉的承载力变小，此时栓钉的剩余抗剪承载力为
，的计算公式可由式(5)转化得到：
(5)
2.3 ANSYS有限元分析模型的建立
1) 单元选取。组合梁中的混凝土板采用solid65单元，混凝土板内钢筋采用link8单元，钢梁采用solid45单元。采用接触对conta173单元和Targe170单元模拟混凝土板与钢梁之间的混凝土板与钢梁之间的黏结。栓钉连接件采用beam188单元进行模拟，beam188单元能较好地模拟栓钉在结合面处承受的复杂剪切应力状态。在栓钉连接处添加3个方向的combine39弹簧单元，模拟栓钉在复杂的剪应力状态下的滑移，其中，竖向弹簧用来模拟单轴拉压，另外2个方向的弹簧刚度较大，用于防止组合梁发生横向滑移与掀起，同时防止数值模拟方程组出现畸变。界面处combine39单元的设置如图2所示[16]。
图2 整体有限元模型中的栓钉形式
Fig. 2 Form of studs in overall finite element model
2) 本构关系选取。混凝土的单轴受压应力应变关系采用文献[19]中建议的本构关系模型。模型所涉及的钢梁、钢筋本构关系都采用双线性等向强化模型(BIOS)与Von Mises屈服准则，栓钉采用Nauyen提出的三折线本构模型[20]。
3) 有限元分析模型的建立。通过ANSYS分析建模，划分单元，得到有限元分析模型如图3所示。模型的支座形式和约束位置与试验设置相同，并参照试验加载方式，加载时将荷载转换为面荷载。先对钢-混凝土组合梁有限元模型进行静力加载计算，验证模型的有效性。将模拟得到的荷载-挠度曲线与试验结果对比，如图4所示。从图4可见：有限元分析曲线与试验曲线吻合较好，说明有限元模型能有效模拟构件的静力受力性能。通过本文方法得到的组合梁的极限承载力与试验结果接近，相对误差为6.4%，试件破坏时的跨中挠度略小于试验结果，相对误差为3.5%。
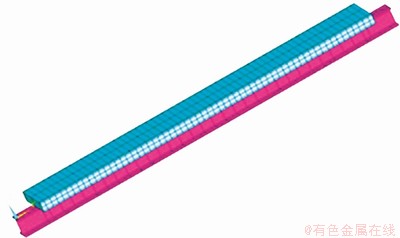
图3 有限元计算模型示意图
Fig. 3 Schematic diagram of finite element calculation model
图4 跨中截面荷载-挠度曲线
Fig. 4 Combined beams span mid-section load-displacement curves
2.4 钢-混凝土组合梁疲劳寿命预测
将组合梁有限元分析模型与式(4)和(5)相结合，模拟计算组合梁的疲劳寿命。利用有限元模型提取组合梁中每个栓钉的剪应力幅值和疲劳荷载上限，利用式(4)和(5)计算栓钉的疲劳寿命和栓钉的剩余承载力，间接引入栓钉的初始缺陷和疲劳裂纹。
在疲劳荷载作用下，组合梁中受力最大的栓钉周围的混凝土最先发生开裂，导致栓钉的承载力迅速下降，当加载次数达到其寿命时，栓钉发生疲劳断裂破坏。在建模计算时，采用单元“生死”的方法，将发生疲劳破坏的栓钉单元及其周围的混凝土单元“杀死”，使其退出工作，然后按新的模型重新计算[21]。第1根栓钉发生破坏时，剩余栓钉尚未达到疲劳寿命，可由式(5)计算剩余有效栓钉的承载力，剪力在剩余栓钉内进行应力重新分布，新的危险栓钉出现。疲劳荷载继续作用，第2根危险栓钉也发生疲劳断裂，退出工作。随着栓钉依次破坏，钢梁和混凝土板之间的组合作用完全丧失，组合梁不能继续承受疲劳荷载，此时的加载次数即为组合梁的疲劳寿命，组合梁的疲劳寿命计算流程如图5所示。建模计算时，为了便于记录栓钉发生疲劳破坏的顺序，对栓钉进行编号，由左边跨开始向右依次增加，栓钉编号如图6所示。
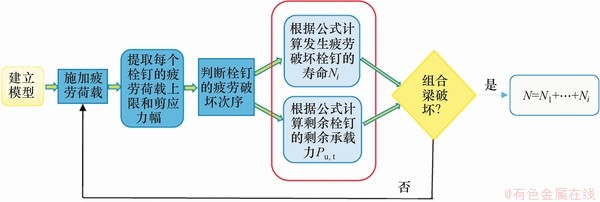
图5 组合梁的疲劳寿命计算流程图
Fig. 5 Fatigue life calculation flowchart of composite beam
图6 组合梁中栓钉编号
Fig. 6 Number of studs in composite beams
采用与试件FSCB-4疲劳试验相同的荷载幅值，对钢-混凝土组合梁有限元模型进行加载求解。
1) 确定危险栓钉编号。根据静力有限元分析结果，距离组合梁端部约1/8处的S3号和S28号栓钉的应力幅最大，为123.824 MPa，将最先发生疲劳断裂破坏；
2) 计算已发生疲劳破坏栓钉的疲劳寿命。根据式(4)计算得到栓钉S3和S28的疲劳寿命N3为892 380次；
3) 去除失效栓钉。在组合梁有限元整体模型中“杀死”栓钉S3和S28所在的单元及其周围的混凝土单元，使其退出工作；
4) 重新施加荷载。重复上述步骤反复计算，直到剪跨内危险栓钉均发生疲劳破坏，此时累加所有发生疲劳断裂栓钉的疲劳寿命，即可得到整个组合梁的疲劳寿命。试件FSCB-4的计算过程如表2所示，累加得到组合梁的疲劳寿命为190.87×104次。
表2 有限元模拟组合梁FSCB-4的疲劳寿命
Table 2 Fatigue life simulation of composite beam FSCB-4
依照与试件FSCB-4同样的流程计算试件FSCB-5的疲劳寿命，结果如表3所示。试件FSCB-4和FSCB-5的疲劳寿命分别为190.87×104次和221.4×104次，与试验数据的相对误差分别为12.28%和6.95%。文献[16]依据S-N曲线及Miner累计损伤理对组合梁试件FSCB-4和FSCB-5的疲劳寿命进行了有限元分析计算，得出的疲劳寿命分别为215.54×104次和262.57×104次，与试验数据的相对误差分别为26.30%和26.85%。与文献[16]的计算结果相比，本文的疲劳寿命计算结果与试验值更吻合。
表3 有限元模拟组合梁的疲劳寿命
Table 3 Fatigue simulation of fatigue life of composite beams
3 锈蚀栓钉钢-混凝土组合梁疲劳寿命预测
3.1 锈蚀栓钉的力学性能退化规律
锈蚀栓钉的力学性能退化主要体现在栓钉自身材料特性的退化，如栓钉极限强度、屈服强度、弹性模量和截面直径等。锈蚀栓钉的弹性模量退化系数
、屈服强度退化系数
、极限强度退化系数
与栓钉的锈蚀率
有关，可分别按式(6)~(8)计算[22-25]。
锈蚀栓钉弹性模量退化系数：
(6)
锈蚀栓钉屈服强度退化系数：
(7)
锈蚀栓钉极限强度退化系数
：
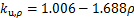(8)
当锈蚀率分别为5%，10%，15%和20%时，栓钉的极限强度和弹性模量等的退化规律如表4所示。
表4 锈蚀栓钉的材料性能退化情况
Table 4 Degradation of material properties of rusted studs
3.2 锈蚀栓钉疲劳寿命预测模型建立
文献[24]表明，腐蚀环境下金属材料的疲劳裂纹扩展仍然接近线性关系，仍然可以使用Paris公式进行描述，但Paris公式中的参数变化并不能直接反映腐蚀环境对构件疲劳寿命的影响。通过引入栓钉疲劳裂纹扩展修正系数和锈蚀栓钉的极限强度修正系数反映腐蚀环境对构件疲劳寿命的影响，在未锈蚀栓钉的疲劳寿命预测模型的基础上，进一步得到锈蚀栓钉的疲劳寿命预测模型[17]：
(9)
式中：
和
为锈蚀栓钉的疲劳裂纹扩展修正系数，分别取1.109和1.014。
同理，由式(9)可以进一步得到锈蚀栓钉在疲劳荷载下的剩余承载力：
(10)
3.3 锈蚀栓钉钢-混凝土组合梁的疲劳寿命预测
以试件FSCB-4为研究对象，综合考虑锈蚀对栓钉极限强度、屈服强度、弹性模量和截面直径等的影响，对栓钉的本构模型和截面直径进行修正，得到锈蚀栓钉钢-混凝土组合梁的有限元计算模型。采用与未锈蚀栓钉钢-混凝土组合梁同样的分析方法，不同锈蚀率下组合梁的疲劳寿命计算过程如图5所示，采用式(9)计算锈蚀栓钉的疲劳寿命，采用式(10)计算锈蚀栓钉在不同疲劳次数后的剩余承载力。栓钉锈蚀率为5%时组合梁的计算过程如表5所示，累加得到锈蚀栓钉组合梁的疲劳寿命为168.90×104次。同理，当锈蚀率为10%，15%和20%时，计算得到组合梁的疲劳寿命分别为142.64×104，99.09×104和38.84×104次。将不同锈蚀率下组合梁的疲劳寿命与未锈蚀组合梁的疲劳寿命进行比较，结果如表6所示。
表5 栓钉锈蚀率为5%时组合梁的疲劳寿命计算
Table 5 Fatigue life calculation of composite beams with 5% corrosion rate of studs
表6 锈蚀组合梁疲劳寿命与完好组合梁疲劳寿命对比
Table 6 Comparison of fatigue life of corroded composite beams and fatigue life of intact composite Beams
由表6可知：当组合梁中栓钉的锈蚀率为5%，10%，15%和20%时，钢-混凝土组合梁的疲劳寿命分别为168.90×104，142.64×104，99.09×104和38.84×104次，其疲劳寿命分别下降11.51%，25.27%，48.08%和79.65%，组合梁的疲劳寿命随栓钉锈蚀率的变化如图7所示。由图7可知：栓钉的锈蚀率对钢-混凝土组合梁的疲劳寿命影响较大，随着锈蚀率增加，组合梁的疲劳寿命逐渐下降。
图7 组合梁的疲劳寿命退化规律
Fig. 7 Fatigue life degradation law of composite beams
4 结论
1) 采用ANSYS软件，结合基于断裂力学理论的栓钉疲劳寿命预测模型和栓钉经过次循环荷载后的剩余承载力计算公式，建立了钢-混凝土组合梁有限元分析模型。
2) 采用本文方法计算得到钢-混凝土组合梁试件FSCB-4和FSCB-5的疲劳寿命分别为190.87×104次和221.4×104次，与试验数据的相对误差分别为12.28%和6.95%。比传统的依据S-N曲线及Miner累计损伤理论的组合梁疲劳寿命有限元分析方法，精度更高，与疲劳试验值吻合得更好。
2) 综合考虑锈蚀率对栓钉极限强度、屈服强度、弹性模量和截面直径等的影响，修正了锈蚀栓钉组合梁有限元分析模型。
3) 栓钉的锈蚀对钢-混凝土组合梁疲劳寿命影响较大，当栓钉的锈蚀率为5%，10%，15%和20%时，钢-混凝土组合梁的疲劳寿命分别为168.90×104，142.64×104，99.09×104和38.84×104次，其疲劳寿命分别下降11.51%，25.27%，48.08%和79.65%。
参考文献：
[1] HUANG Dunwen, WEI Jun, LIU Xiaochun, et al. Experimental study on long-term performance of steel-concrete composite bridge with an assembled concrete deck[J]. Construction and Building Materials, 2019, 214: 606-618.
[2] HANSWILLE G, PORSCH M, USTUNDAG C. Resistance of headed studs subjected to fatigue loading, Part I: experimental study[J]. Journal of Constructional Steel Research, 2007, 63(4): 475-484.
[3] ABU-SENA A B, SHAABAN I G, SOLIMAN M S, et al. Effect of geometrical properties on strength of externally prestressed steel–concrete composite beams[J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 2020, 173(1): 42-62.
[4] APOSTOLOPOULOS C A. Mechanical behavior of corroded reinforcing steel bars S500s tempcore under low cycle fatigue[J]. Construction and Building Materials, 2007, 21(7): 1447-1456.
[5] ZHANG W, YUAN H. Corrosion fatigue effects on life estimation of deteriorated bridges under vehicle impacts[J]. Engineering Structures, 2014, 71: 128-136.
[6] KASHANI M M, LOWES L N, CREWE A J, et al. Finite element investigation of the influence of corrosion pattern on inelastic buckling and cyclic response of corroded reinforcing bars[J]. Engineering Structures, 2014, 75: 113-125.
[7] XI Y P, WILLAM K, WEYERS R E. Accelerated testing and modeling of concrete durability subjected to coupled environmental and mechanical loading[J]. Long Term Durability Structure Material, 2001: 45-56.
[8] CHEN Ju, ZHANG Haipeng, YU Qianqian. Static and fatigue behavior of steel-concrete composite beams with corroded studs[J]. Journal of Constructional Steel Research, 2019, 156: 18-27.
[9] CHEN Ju, ZHAO Yuxi, WU Lin, et al. Experimental investigation and design of corroded stud shear connectors[J]. Advances in Structural Engineering, 2016, 19(2), 218-226.
[10] CAO Guohui, YANG Liang, ZHANG Wang, et al. Longterm mechanical properties of steel-concrete connectors subjected to corrosion and load coupling[J]. Journal of Materials in Civil Engineering, 2018, 30(5): 04018058.
[11] WANG Weilun, CHEN Ju, JIN Weiliang. Experimental investigation of corroded stud shear connectors subjected to fatigue loading[J]. Journal of Materials in Civil Engineering, 2017, 29(1): 04016175.
[12] 袁佩. 基于断裂力学的铆接钢桥疲劳寿命研究[J]. 公路交通技术, 2013, 29(6): 66-69.
YUAN Pei. Research on fatigue life of riveted steel bridges based on fracture mechanics[J]. Technology of Highway and Transport, 2013, 29(6): 66-69.
[13] 王宇航, 聂建国. 基于断裂力学的组合梁栓钉疲劳性能[J]. 清华大学学报(自然科学版), 2009, 49(9): 1467-1470.
WANG Yuhang, NIE Jianguo. Fatigue behavior of studs in a composite beam based on fracture mechanics[J]. Journal of Tsinghua University(Science and Technology), 2009, 49(9): 1467-1470.
[14] 荣学亮, 黄侨, 任远. 栓钉连接件锈蚀后静力性能和抗疲劳性能的试验研究[J]. 土木工程学报, 2013, 46(2): 10-18.
RONG Xueliang, HUANG Qiao, REN Yuan. Experimental study on static and fatigue behaviors of stud connectors for composite beams after corrosion[J]. China Civil Engineering Journal, 2013, 46(2): 10-18.
[15] WANG Yuhang, NIE Jianguo, LI Jianjun. Study on fatigue property of steel-concrete composite beams and studs[J]. Journal of Constructional Steel Research, 2014, 94: 1-10.
[16] 李自林, 邢颖, 韩庆华, 等. 弹性混凝土与钢组合梁的疲劳性能分析及寿命预测[J]. 东南大学学报(自然科学版), 2015, 45(1): 165-171.
LI Zilin, XING Ying, HAN Qinghua, et al. Fatigue behavior analysis and life prediction of elastic concrete and steel composite beam[J]. Journal of Southeast University(Natural Science Edition), 2015, 45(1): 165-171.
[17] KUANG Yachuan, WANG Kun, HE Yuhao, et al. Fatigue behavior of corroded stud based on crack growth theory[J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 2020(5): 1-1.
[18] 郭建生, 孙国正. 用断裂力学法估算焊接钢结构的疲劳寿命[J]. 起重运输机械, 1999(10): 9-12.
Guo Jiansheng, Sun Guozheng. Fracture mechanics method for estimating the fatigue life of welded steel structure[J]. Hoisting and Conveying Machinery, 1999(10): 9-12.
[19] GB 50010—2010. 混凝土结构设计规范[S].
GB 50010—2010. Code for design of concrete structures[S].
[20] NGUYEN H T, KIM S E. Finite element modeling of push-out tests for large stud shear connectors[J]. Journal of Constructional Steel Research, 2009, 65(10/11): 1909-1920.
[21] 姜绍飞, 王鹏, 吴兆旗. 钢-混凝土组合梁疲劳性能的有限元分析[J]. 沈阳建筑大学学报(自然科学版), 2009, 25(1): 111-115.
JIANG Shaofei, WANG Peng, WU Zhaoqi. Finite element analysis on fatigue behavior of steel-concrete composite beams[J]. Journal of Shenyang Jianzhu University(Natural Science), 2009, 25(1): 111-115.
[22] AKIIKE S, NOSE H, HIROTA Y, et al. Comparison of three testing methods of fracture toughness using indirect composite[J]. Nihon Hotetsu Shika Gakkai Zasshi, 2008, 52(1): 49-58.
[23] 匡亚川, 余志武, 龚匡晖, 等. 栓钉锈蚀与抗剪承载力试验研究[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(2): 381-385.
KUANG Yachuan, YU Zhiwu, GONG Kuanghui, et al. Experiment research on stud corrosion and structural function deterioration of push-out specimens[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2013, 37(2): 381-385.
[24] 余志武, 石卫华, 匡亚川. 锈蚀栓钉力学性能试验研究[J]. 中南大学学报(自然科学版), 2014, 45(1): 249-255.
YU Zhiwu, SHI Weihua, KUANG Yachuan. Experimental study on mechanical properties of corroded stud[J]. Journal of Central South University(Science and Technology), 2014, 45(1): 249-255.
[25] 鲍蕊, 董彦民, 张建宇, 等. 腐蚀条件下铝合金疲劳裂纹扩展试验及模型[J]. 航空材料学报, 2006, 26(6): 12-16.
BAO Rui, DONG Yanmin, ZHANG Jianyu, et al. Fatigue crack growth experiments and model in corrosive environment for aluminum alloy[J]. Journal of Aeronautical Materials, 2006, 26(6): 12-16.
(编辑 秦明阳)
收稿日期： 2020 -05 -15; 修回日期： 2020 -07 -26
基金项目(Foundation item)：国家自然科学基金资助项目(51878663) (Project(51878663) supported by the National Natural Science Foundation of China)
通信作者：匡亚川，博士，副教授，从事钢-混凝土组合梁桥结构疲劳寿命预测研究；E-mail: kuangyachuan@csu.edu.cn
引用格式： 匡亚川, 陶莉, 贺宇豪. 锈蚀栓钉钢-混凝土组合梁的疲劳寿命预测模型[J]. 中南大学学报(自然科学版), 2021, 52(3): 770-778.
Citation: KUANG Yachuan, TAO Li, HE Yuhao. Fatigue life prediction model of corroded studded steel-concrete composite beam[J]. Journal of Central South University(Science and Technology), 2021, 52(3): 770-778.
