风电变桨行星减速机的动力学性能仿真

朱浩，成伟，贾国海，李磊

(湖南大学 机械与运载工程学院，湖南 长沙，410082)

摘要：利用虚拟样机技术对1.5 MW风电变桨行星减速机进行运动学、动力学仿分析，并在此基础上对箱体进行有限元模态分析。用接触力模拟齿轮啮合力的方法得出了行星减速机3级内齿圈的动载荷时域、频域变化规律，并对第3级内齿圈进行动载荷齿面接触强度校核。研究结果表明：减速机传动比仿真结果与理论计算结果相差仅为0.01，验证了建模方法的正确性；该行星传动属于具有较高可靠度的行星传动；在额定工况下，箱体固有频率与各内齿圈内齿啮合频率相差较大，不会发生共振现象。

关键词：行星减速机；虚拟样机；运动学；动力学仿真；模态分析

中图分类号：TK 83          文献标志码：A         文章编号：1672-7207(2011)10-3059-07

Dynamic performance simulation on wind-power pitch planetary reducer

ZHU Hao, CHENG Wei, JIA Guo-hai, LI Lei

(College of Mechanical & Vehicle Engineering, Hunan University, Changsha 410082, China)

Abstract: 1.5 MW wind-power pitch planetary reducer was analyzed with kinematics, and dynamics simulation and the box were carried out based on the finite element modal. To simulate the gear meshing force by using contact force, the method obtains the dynamic load time domain, frequency domain variation of three planetary ring gear reducers, and the intensity of tooth contact dynamic load of the third stage ring gear was checked. The results show that the tolerance between the simulation results and theoretical calculation results of the gear transmission ratio is only 0.01, which verifies the correctness of the modeling approach. The planetary transmission has high reliability. In nominal condition, the natural frequency of cabinet is greater than the circle gear tooth meshing frequency, so the resonance phenomenon will not appear.

Key words: planetary reducer;virtual prototyping; kinematics, dynamics simulation; modal analysis

风力发电作为可再生清洁能源在全球得到了快速、稳步发展^[1-3]。风电齿轮箱作为风力发电系统的重要部件, 既要求其传递功率大、体积小、密度低，又要求其满足振动小、噪声低的要求。齿轮箱的工作是否正常，将直接影响到风电机组整体能否正常运行。目前，国内外针对风力发电机齿轮传动系统的研究已处于发展阶段，相关研究主要集中在行星系动态性能以及新型齿轮传动的设计研究上，如：Kahraman等^[4-5]通过对行星轮系建立数学模型，主要考虑了行星轮系中时变刚度引起的激励，对行星轮系的振动进行了系统研究，在一定程度上揭示了行星轮系中振动现象的规律；孙涛等^[6]建立的行星齿轮传动的弯扭耦合非线性动力学模型考虑了横向振动、时变刚度、轮齿间间隙等多种因素的影响；洪清泉等^[7]对多级齿轮传动系统进行了动力学仿真；秦大同等^[8]以整个传动系统包括行星轮系和平行轴系为研究对象，基于动力学对系统的可靠性和设计参数进行了优化。在此，本文以1.5 MW风电变桨驱动行星减速机为研究对象，通过简化模型的办法建立其多刚体动力学模型及箱体的有限元模型，并进行动力学性能仿真分析，验证减速机设计的合理性，以便为其优化设计以及减振降噪提供参考。

1  变桨减速机的工作原理

由于风力机每个叶片都需拥有独立的变桨驱动系统，要求其体积小、密度低、传动功率大，目前变桨驱动减速机大多为NGW型行星齿轮减速机。本文研究的行星减速机传动机构由3级行星轮系组成，每一级结构相似，都为NGW型传动。图1所示为NGW型行星传动简图。

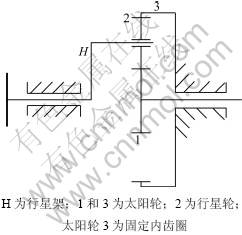
图1  NGW型行星传动简图

Fig.1  NGW type planetary transmission diagram

每级传动比计算公式^[9]为：

                 (1)

式中：z₃为内齿圈齿数；z₁为太阳轮齿数。根据行星轮减速机各齿轮齿数可得出：第1级传动比i₁=6.353；第2级传动比i₂=5.043；第3级传动比i₃=4.091；总传动比i=i₁·i₂·i₃=131.068。

2  行星轮减速机虚拟样机模型的  建立

考虑采用目前国际上应用最为广泛的虚拟样机分析软件ADAMS进行建模。ADAMS采用广泛流行的多刚体系统动力学理论中的拉格朗日方程，建立系统的动力学方程。由于ADAMS本身的三维建模功能不强，故对于像减速机这样的复杂机械系统模型采用专业的CAD软件进行建模，然后，通过专业接口软件来导入ADAMS^[10-11]。

2.1  减速机三维实体建模与虚拟装配

依据1.5 MW风电机组变桨驱动减速机的各设计技术要求，绘制减速机各零部件以及总装配图的CAD二维图形。然后，利用Pro/E三维实体建模软件对变桨距驱动减速机装置零部件进行三维造型。为了降低整个系统的建模难度，在不影响整机工作性能仿真的前提下，对减速机模型进行简化，只对与传动有关的主要零部件进行建模。在减速器各零件三维模型的基础上，进行装配建模。通过装配，可以形成产品的总体装配图、检查零件之间是否发生干涉等。减速机装配图如图2所示。

图2  1.5 MW变桨驱动行星减速机总装配图

Fig.2  Assembly drawing of 1.5 MW pitch drive planetary gear

2.2  Pro/E和ADAMS之间模型转换

建立了减速机的三维模型后，必须将减速器装配模型传递到ADAMS/View中。对于Pro/E和ADAMS的模型传递，MDI公司提供了专用接口模块Mechanism/Pro。二者采用无缝连接的方式，不需要退出Pro/E应用环境，就可以将装配好的总成根据其运动关系定义为机械系统模型。在Mechanism/Pro中定义好各刚体后就可以把模型数据直接导入ADAMS/View中。图3所示为导入ADAMS后的减速机刚体模型。

图3  ADAMS中的减速机刚体模型

Fig.3  Rigid body model of reducer in ADAMS

得到刚体模型以后，就可以在View环境中对其刚体、约束、驱动和力进行修改或新建。变桨减速机主要由3级行星轮系减速机构组成，依据其机械系统的运动关系，建立铰接副、齿轮副、固定副、接触力、驱动、力矩等运动学、动力学模型。图4所示为建立好的1个基于ADAMS 1.5 MW变桨驱动减速机多体动力学模型。

图4  基于ADAMS的1.5 MW变桨驱动减速机多体动力学模型(箱体隐藏)

Fig.4  1.5 MW variable propeller-driven gearbox multi-body dynamic model based on ADAMS

3  减速机运动学和动力学仿真分析

3.1  传动比的验证

本文所设计的减速机理论计算传动比为131.07，额定输入转速为2 500 r/min(即261.80 rad/s)，额定输出转速为18.96 r/min(即1.99 rad/s)尖峰输出功率为15 kW。为避免仿真时输入轴转速发生突变，在高速输入轴上加驱动转速(Motion)函数为step(time，0，0，0.2，100)。注意将Tyep选项选为Velocity。在ADAMS/ View 模块仿真工具中输入仿真时间为5 s ,仿真工作步数为 150 ,仿真结果如图5所示。从图5可见：减速机运行平稳时，测量得到输入轴角速度为118.681 3 rad/s，输出轴角速度为0.905 4 rad/s，由此计算得到的仿真传动比为131.08。与理论计算结果相差仅0.01，验证了所建立的多体动力学模型的正确性。

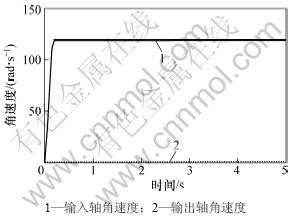
图5  输入轴和出轴角速度仿真结果

Fig.5  Input shaft and output shaft of angular velocity simulation results

3.2  齿轮动态啮合力仿真分析

为了获得齿轮传动过程中的动态啮合力，结合Hertz弹性接触理论，采用ADAMS软件中的接触力来进行模拟。

3.2.1  接触力的定义及选择

在ADAMS中有2种计算接触力的方法：一种是补偿法(Restitution)；另一种是冲击函数法(Impact)。补偿法需要确定2个参数，即惩罚系数和补偿系数。冲击函数法是根据Impact函数来计算2个构件之间的接触力。接触力由2部分组成：一个是由于2个构件之间的相互切入而产生的弹性力；另一个是由相对速度产生的阻尼力。应用Impact函数f来计算接触力。

Impact函数的表达式f为：

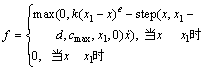        (3)

式中：k为接触刚度；x为2个物体碰撞过程中的实际距离；e为非线性指数；c_max为阻尼系数；d为击穿深度；x₁为1个位移开关量(用来确定单侧碰撞是否起作用)；为速度变量。当2个物体间实际距离x小于开关变量x₁时，则这2个物体间产生接触力。

3.2.2  接触力中参数的确定

轮齿接触所引起的冲击力，可以由2个变曲率半径柱体撞击问题来求解。此问题可以直接从Hertz静力弹性接触理论中得到^[12]。根据Hertz碰撞理论，考虑接触面为圆形，有：

            (4)

得撞击时接触法向力P和变形δ的关系为：

P=kδ^3/2

式中 ：；1/R=1/R₁+1/R₂；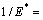

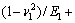
；k为接触刚度系数，且取决于撞击物体材料和结构形状；ν₁和ν₂分别为2个齿轮材料的泊松比；E₁和E₂分别为2个齿轮材料的弹性模量；R₁和R₂分别为2个齿轮啮合点处的当量半径。

依据各行星啮合齿轮的设计参数和材料参数以文献[13]推导出斜齿轮的刚度系数k计算公式为：

     (5)

其中：k为刚度系数；E^*为综合弹性模量；ρ为曲率半径；u为传动比；d为分度圆直径；α_t和α′_t分别为斜齿轮传动的端面分度压力角和端面啮合角；β_b为齿轮螺旋角。

根据钢材料的接触参数，接触力指数项取1.5，阻尼值取50 N·s/mm，接触有效深度取0.1 mm。

3.2.3  齿轮啮合力仿真分析

减速机的额定工况仿真中，在高速输入轴上加转速驱动(MOTION)，为了使输出轴以额定输出转速(1.99 rad/s)运转，同时在仿真过程中转速不出现突变，利用STEP函数使输入转速在0.2 s内由0 rad/s增加到261.80 rad/s，函数式为step(time，0，0，0.2，220.46)。在输出端加上负载力矩。负载力矩可按

             (6)

来计算，得7.55×10⁶ N·mm。为使负载平缓地加载可以采用函数Step(time，0，0，0.2，7.55×10⁶)赋值，在ADAMS/ View 模块仿真工具中输入仿真时间为  1 s，仿真工作步长为0.001 s，用GSTIFF积分器进行仿真求解。

由于此减速机传动比为131，当输入轴转131圈时，输出轴才转1圈。求解精度受ADAMS求解器积分步长的影响，为了较好地对齿轮啮合进行仿真，对3级行星轮系单独进行仿真。第1级行星轮系的输出作为第2级行星轮系的输入，第2级行星轮系的输出作为第3级行星轮系的输入。参数设置参照整机额定工况仿真测出的数据。图6所示为3级行星轮系的虚拟样机模型图。

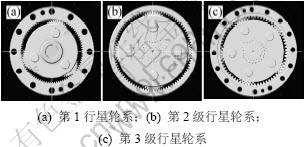
图6  3级行星轮系虚拟样机模型

Fig.6  Three virtual prototype model of planetary gear

对第1级行星轮系进行仿真时，step size取  0.000 1 s，仿真时间为0.2 s。对第2级行星轮系进行仿真时，step size取0.001，仿真时间为2 s；第3级行星轮系进行仿真时，工作步长取0.01，仿真时间为10 s。为了后面的箱体模态分析，在这里仅对减速机各内齿圈的动态啮合力进行分析。图7~9所示为内齿圈轮齿动态接触力时域变化曲线及频域变化曲线。

从图7~9可以看出：齿啮合力呈周期性变化，这主要是行星轮减速机装配误差以及行星轮的运动特性引起的。第3行星轮内齿圈内齿的啮合力比较大，因此，对其进行齿面接触强度校核；啮合力最大值为17 115 N，齿轮材料为42CrMo，工作寿命为20 a，最小安全系数取1.25，经计算得许用接触应力为976 MPa，接触应力为811.57 MPa。强度校核结果表明：该行星传动具有较高可靠度。由轮齿啮合频率为每秒转过的圈数与齿数的乘积，内齿圈虽然是固定的，但可以取相对的行星轮的公转速度进行计算。代入相应理论数据可得：第1~3级行星轮系的内齿圈啮合频率分别为596.8，120.9和21.6 Hz。从图7~9可得：第1级行星轮系的内齿圈啮合频率为596.8 Hz，与理论计算指相差仅1.1 Hz；第2级行星轮系的内齿圈啮合频率为121.1 Hz，与理论计算值相差0.2 Hz；第3级行星轮系的内齿圈啮合频率为21.6 Hz，与理论计算结果相符。

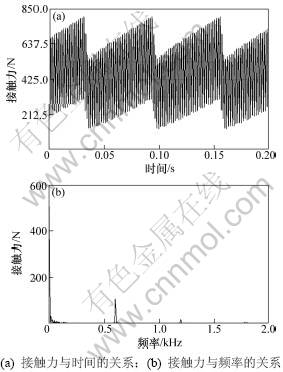
图7  第1级内齿圈内齿动态接触力时域、频域变化曲线

Fig.7  Time domain, frequency domain curves of gear dynamic contact force in first class ring gear

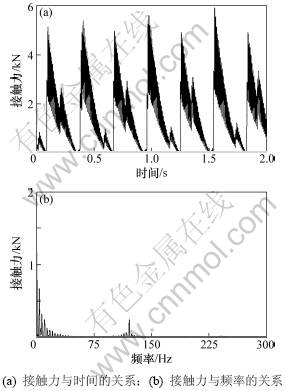
图8  第2级内齿圈内齿动态接触力时域、频域变化曲线

Fig.8  Time domain, frequency domain curves of gear dynamic contact force in second class ring gear

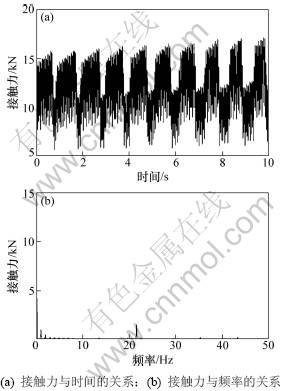
图9  第3级内齿圈内齿动态接触力时域和频域变化曲线

Fig.9  Time domain and frequency domain curves of gear dynamic contact force in third class ring gear

4  箱体有限元模态分析

4.1  箱体有限元模型的建立

由于内齿圈与箱体直接相连，第1级和第3级内齿圈还是参与构成箱体的一部分，因此，把各内齿圈看作是箱体的一部分。在箱体的有限元建模中进行一些合理简化，忽略箱体上一些小螺栓孔、销孔、油嘴孔等。这简化不会对齿轮箱体的质量及刚度产生大的影响，完全保证计算精度要求^[14-15]。

利用大型商业集成软件LMS Virtual. Lab中的Meshing模块建立了该行星减速器箱体的有限元分析模型,单元类型为TETRA4，共计5 5824个节点数和 259 432个单元数, 如图10所示。

图10  行星减速机箱体有限元模型

Fig.10  Planetary reducer body finite element model

4.2  箱体有限元模态分析

在采用LMS Virtual. Lab中的Structures有限元进行分析之前，定义处理模块中箱体的材料属性(箱体材料为QT400—15)，按照实际安装情况定义边界条件,求解的频率阶数设为20阶，加载NASTRAN的SOL103模块进行模态分析，得到20阶箱体的固有频率及对应的固有振型。表1所示为齿轮箱箱体的前10 阶固有频率。结合前面求得的3级内齿圈啮合冲击频率，注意到图7中曲线在1 193.2 Hz处有1个小波峰，与该减速机箱体的第3阶固有频率相近，但这小波峰主要是由行星轮减速机装配误差引起，在现实运行中可通过行星架与太阳轮之间设置的浮动垫来消除，因此，减速机在额定工况工作时，减速机箱体不会产生共振。图11所示为减速机箱体的前3阶振型。其中：第l阶频率为835.0 Hz，大体沿轴向摆动；第2阶频率为851.6 Hz，大体沿横向摆动；第3阶频率为1 259.1 Hz，大体绕垂向扭转。

图11  行星减速机箱体前3阶固有振型

Fig.11  First three natural vibration modes of planetary reducer box

表1  行星减速机箱体前10阶固有频率

Table 1  First 10 natural frequencies of planetary reducer box

5  结论

(1) 建立了变桨减速机的三维实体模型，并在ADAMS中建立减速机的虚拟样机模型，实现了其在额定工况的动力学仿真，得到了各级内齿圈内齿的动态啮合力时域、频域规律，且仿真结果与理论计算结果相吻合，达到了设计要求，说明虚拟样机模型的准确性以及仿真的可信性，也验证了风电变桨减速机设计的合理性。

(2) 在额定工况中，行星轮轮齿与内齿圈内齿的啮合冲击激励，不会引起减速机箱体共振。

(3) 通过动力学仿真分析得出的结果，可为该变桨减速机传动系统及其他传动系统的强度校核、振动噪声分析等提供参考，在后面的研究工作中，其内齿圈内齿的动载荷将作为减速箱箱体结构噪声预测的载荷边界条件。

参考文献：

[1] Sanchez I. Adaptive combination of forecasts with application to wind energy[J]. International Journal of Forecasting, 2008, 24(4): 679-693.

[2] Thorne S. Towards a framework of clean energy technology receptivity[J]. Energy Policy, 2008, 36(8): 2831-2838.

[3] 李志梅, 赵东标. 风电现状及发展趋势[J]. 风机技术, 2007(4): 63-68.
LI Zhi-mei, ZHAO Dong-biao. Current situation and developing trend of wind power technique[J]. Compressor Blower & Fan Technology, 2007(4): 63-68.

[4] Kahraman A. Planetary gear train dynamics[J]. ASME Journal of Mechanical Design, 1994, 116: 713-720.

[5] Parker R G, AGashe V, Vliayakar S M. Dynamic response of a planetary gear system using a finite element/contact mechanics model[J]. Transactions of the ASME Journal of Mechanical Design, 2000, 122: 304-310.

[6] 孙涛, 沈允文, 孙智民, 等. 行星齿轮传动非线性动力学模型与方程[J]. 机械工程学报, 2002, 38(3): 6-10.
SUN Tan, SHEN Yun-wen, SUN Zhi-min, et a1. Study on nonlinear dynamic behavior of planetary gear train dynamic model and governing equation[J]. Chinese Journal of Mechanical Engineering, 2002, 38(3): 6-10.

[7] 洪清泉, 程颖. 基于ADAMS的多级齿轮传动系统动力学仿真[J]. 北京理工大学学报, 2003, 23(6): 690-693.
HONG Qing-quan, CHENG Ying. Dynamic simulation of multistage gear train system in ADAMS[J]. Transactions of Beijing Institute of Technology, 2003, 23(6): 690-693.

[8] 秦大同, 邢子坤, 王建宏. 基于动力学和可靠性的风力发电齿轮传动系统参数优化设计[J]. 机械工程学报, 2008, 47(7): 24-31.
QING Da-tong, XING Zi-kun, WANG Jian-hong. Optimization design of system parameters of the gear transmission of wind turbine based on dynamics and reliability[J]. Chinese Journal of Mechanical Engineering, 2008, 47(7): 24-31.

[9] 渐开线齿轮行星传动的设计与制造编委会. 渐开线齿轮行星传动的设计与制造[M]. 北京: 机械工业出版社, 2002: 188.
Involute Gear Planetary Transmission Design and Manufacturing Editorial Board. Involute gear planetary transmission design and manufacturing[M]. Beijing: Mechanical Industry Press, 2002: 188.

[10] 石博强, 申焱华, 宁晓斌, 等. ADAMS基础与工程范例教程[M]. 北京: 中国铁道出版社, 2007: 9.
SHI Bo-qiang, SHEN Yan-hua, NING Xiao-bing, et al. ADAMS basis and example tutorial[M]. Beijing: China Railway Press, 2007: 9.

[11] 李增刚. ADAMS入门详解与实例[M]. 北京: 国防工业出版社, 2009: 18.
LI Zen-gang. ADAMS detailed introduction and examples[M]. Beijing: National Defense Industry Press, 2009: 18.

[12] Johnson K L. Contact mechanics[M]. Cambridge: Cambridge University Press, 1985: 235.

[13] 毕凤荣, 崔新涛, 刘宁. 渐开线齿轮动态啮合力计算机仿真[J]. 天津大学学报, 2005, 38(11): 991-994.
BI Feng-rong, CUI Xin-tao, LIU Ning. Computer simulation for dynamic meshing force of involute gears[J]. Journal of Tianjin University, 2005, 38(11): 991-994.

[14] 常山, 尹逊民. 传动齿轮箱体的振动模态分析[J]. 舰船科学技术, 2000(5): 41-49.
CHANG Shan, YIN Xun-ming. Transmission gear-box vibration modal analysis[J]. Ship Science And Technology, 2000(5): 41-49.

[15] 范江东, 潘宏侠. 齿轮箱箱体的有限元模态与实验模态分析[J]. 煤矿机械, 2010, 31(5): 92-93.
FAN Jiang-dong, PAN Hong-xia. Finite element modality and test modality analysis of gearbox-box[J]. Coal Mine Machinery, 2010, 31(5): 92-93.

(编辑 陈灿华)

收稿日期：2010-11-25；修回日期：2011-01-28

基金项目：湖南省教育厅优秀青年基金资助项目(08B042)

通信作者：朱浩(1972-)，男，湖南攸县人，博士，副教授，从事车辆工程/动力机械研究；电话：13975166318；E-mail：zhu1201_1@163.com