DOI: 10.11817/j.issn.1672-7207.2016.07.021
结合领域知识和多特征表示的唐卡破损区域分割算法
胡文瑾1, 2,王维兰1,刘仲民2
(1. 西北民族大学 数学与计算机科学学院,甘肃 兰州,730030;
2. 兰州理工大学 电气工程与信息工程学院,甘肃 兰州,730050)
摘要:针对佛像类唐卡中出现的一致性破损区域的分割进行研究。首先对头光区域投影,利用一维函数对称性检测方法得到图像的对称轴,提出基于对称轴的分块分割方法得到初始分割结果;然后利用Gabor变换提取纹理特征,结合Lab空间颜色特征,构造多尺度多特征集合,最后采用K最近邻分类算法(K-Nearest Neighbor, KNN)得到一致性破损区域的模板。研究结果表明:该方法对于具有对称性的佛像类破损唐卡图像中出现的一致性破损区域的分割效果良好。
关键词:唐卡;一致性破损区域;图像分割;镜像对称;多特征表示
中图分类号:TP391 文献标志码:A 文章编号:1672-7207(2016)07-2326-08
Damaged region segmentation of Thangka based on domain knowledge and multi-feature
HU Wenjin1, 2, WANG Weilan1, LIU Zhongmin2
(1. School of Math and Computer Science, Northwest University for Nationalities, Lanzhou 730030, China;
2. School of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China)
Abstract: A method was proposed to segment the consistent broken area of Buddha Thangka. Firstly, the head light area was projected and the symmetry axis was obtained by one-dimensional function symmetry detection method, and then the initial segmentation result was received based on the symmetric axis block segmentation. Secondly, the texture feature was extracted by Gabor transform, and the multi-scale features set was constructed combined with the Lab color space feature. The consistent broken area template was ultimately achieved by K-Nearest Neighbor (KNN) classification. The results show that this algorithm has an effective segmentation on the consistent broken area of the Buddha Thangka.
Key words: Thangka; consistent broken area; image segmentation; reflectional symmetries; multi-feature representation
唐卡是用彩缎装裱而成的卷轴画,历来被藏族人民视为珍宝,是藏族文化中最为著名的一种宗教艺术品。但由于制作材料以及保存不当等原因,随着时间的推移,部分珍品出现了颜料龟裂、褪色和脱落等损害,亟待抢救和整理。采用数字化修复的手段不仅为画师进行手工修复提供借鉴,而且还可以弥补手工修补的缺陷,近年来受到了研究者的广泛关注[1-3]。工作者首先手工选定破损区域即待修复区域,采用基于纹理合成、变分偏微分方程或稀疏表示的方法对其进行修复,取得了较理想的效果。但对于那些破损区域比较复杂的图像、手工标注难度较大,因此,破损区域的自动分割显得尤为必要。图像分割作为前沿学科充满了挑战,研究人员不断将相关领域出现的新理论和新方法应用到图像分割中。徐胜军等[4]提出了一种基于融合边缘特征的区域MRF模型的图像分割方法,利用局部区域信息建立了局部空间加权的GMM模型,同时建立了GMM模型参数的估计算法,把图像的边缘特征有效融合到区域MRF模型中。李传龙等[5]采用虚拟的符号距离函数,依靠待检测目标局部灰度高斯加权均值来驱动活动轮廓的演化,提出了一种能够分割灰度不均匀图像的新颖活动轮廓模型。张泽均等[6]利用方向边缘强度信息,建立了一种新的边缘惩罚SAR图像分割模型。曹家梓等[7]利用分数阶微分运算提取图像纹理细节和边缘轮廓信息,与灰度共生矩阵提取的纹理空间分布特征相结合,获得了完备的图像纹理信息,在分割后处理过程中利用模糊熵准则对分割结果进行进一步优化。上述方法都针对特定的方法或问题提出了效果良好的图像分割模型,许新征等[8]进一步指出,面向专门领域的应用也是图像分割技术的发展趋势之一。然而唐卡图像结构复杂、纹理丰富,破损区域有时和周围像素灰度比较接近,有时表现为细小的划痕,和图像中固有的纹理单元无法区分,单纯的基于灰度或颜色信息的图像分割,在整幅图像中利用边缘或寻找阈值或聚类,忽略了唐卡图像的纹理结构、布局等语义信息势必造成结果的不准确,所以寻找适合唐卡图像的分割方法尤为重要。胡文瑾等[9]对于唐卡中出现的垂直(或水平)方向的细微折痕进行了自动检测算法研究。刘华明等[10]对灰度唐卡图像中出现的色彩脱落的斑块进行检测,利用阈值分割、形态学分割、分块分割得到潜在破损区域,然后通过去除小面积区域、结合领域知识最终得到了斑块破损结果。但是小面积区域和伪破损区域的剔除须依靠较多的人工交互,自动化程度不高,此外,领域知识如何获取并应用于图像破损区域分割中并没有提及。本文作者充分利用唐卡图像构图、布局的领域知识,在提取对称轴的基础上,首先进行基于对称轴的分块分割,得到破损区域潜在的初始分割结果;考虑到唐卡图像结构特征明显、纹理丰富、颜色多样的特点,在初始分割的基础上,提取纹理和颜色特征,构造融合多尺度、多特征的分类器,通过分类最终得到表征破损区域的模板。
1 唐卡图像的破损形式及原因
唐卡艺术历史悠久,目前13世纪以前的作品存世量已经很少,多数是17世纪及18世纪的作品。随着时间的推移,唐卡都或多或少地受到损害,其主要表现为唐卡质地变脆、褪色、颜色脱落、霉菌、折皱和虫蛀等。出现这些损害的原因一方面是由于唐卡的制作材料(主要是纺织品如动、植物纤维)、颜料以及白粉,易受湿度的影响出现起皱、变色和颜料龟裂;受光辐射易造成颜料的褪色;受霉菌的影响出现颜料脱落;受虫蛀的影响出现文物孔洞等。另一方面,是由于人为有意识或无意识的破坏造成的折裂或颜料脱落等。然而不管是哪种形式,从图像处理角度来看,破损区域处相比其周围像素均出现了较大的灰度突变。
2 唐卡破损区域分割算法
唐卡图像题材众多,涉及包括宗教、历史、风土人情、神话、建筑、历法和藏医藏药等,从整体上看,反映宗教内容的画卷占总存量的80%以上。而唐卡的绘制必须严格遵守宗教仪轨而不能自由创作,如人物造像应该按照《造像度量经》等经书中规定的比例[11];同时在唐卡绘制过程中也积累和沉淀了画师历代传承的藏族、汉族、印度、尼泊尔的艺术传统和审美趣味,并最终形成了固定的审美范式,例如唐卡的“构图严谨、讲究对称”。由此,在图像分割时若能利用唐卡图像的这一领域知识,将会极大地提高分割的准确性。另一方面,通过对破损区域的底层特征进行分析,发现:1) 破损从形状上分为块状、斑点或线状。不管是哪种形式,都属于非纹理。而在唐卡中不同的纹理特征尺度不同,如在表现本尊时往往其身光后包含了细小的线条,需要在小尺度下进行分析;而祥云、法器、坐台及装饰纹样等图形,需要对其在大尺度下进行分析。2) 破损区域的灰度特征表现为与周围像素相比较暗的区域,或者较亮的区域,并且从全局上呈现为一个或有限个颜色一致的区域,故颜色特征在后续分割过程中也不容忽视。为此,综合考虑纹理和颜色特征,共同组成特征集合,通过构造分类器对初始分割结果图像分类可以有效地获取破损区域的模板。综上所述,针对佛像类唐卡中出现的一致性破损区域,本文作者提出自动分割算法,具体过程如图1所示。
2.1 破损区域初始分割
初始分割希望尽可能地包含破损区域的全部信息,由于破损区域与周围像素颜色相差不多,若在整幅图像中只采用1个阈值,则势必会丢失部分破损区域。分块分割法自左向右、自上而下地对图像进行矩形分块[12],然后在各块内再阈值化分割,从而最大程度地保留了破损信息。但是这类方法忽略了图像中包含的对象信息,易将1个目标分成多个区域,并为后续的处理带来困难;基于对象的分块分割[13]对于包含物体单一的图像取得了较好的效果,但是唐卡图像中的结构复杂、包含对象众多,该类方法的直接应用存在一定困难。然而,唐卡图像在构图时存在对称性,尤其是佛像类,为此,本文以对称轴为基准采用分块采样的策略进行初始分割。
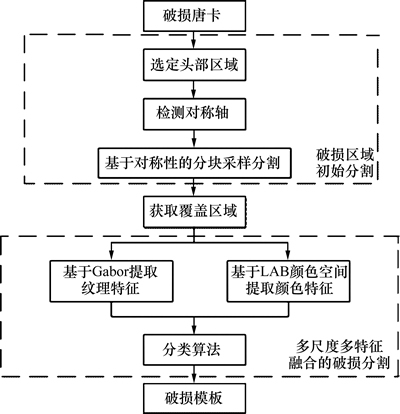
图1 唐卡破损区域分割流程图
Fig. 1 Flowchart of segment damaged regions of Thangka
考虑到唐卡图像大多为左右对称,以对称轴l为轴,将图像可分为左右2部分,即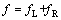 ,fL为左边图像的灰度,fR为右边图像的灰度。以l为基准分别向左右边界延伸,分块时每次选取图像块
,fL为左边图像的灰度,fR为右边图像的灰度。以l为基准分别向左右边界延伸,分块时每次选取图像块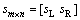 ,其中s L,s R分别为
,其中s L,s R分别为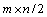 的像素块。
的像素块。
为了有效地处理,边界采用补0的方法来扩充。
2.1.1 对称性检测
对称性检测算法大致分为2类:基于全局特征的和基于局部特征的方法。全局特征[14-16]将整个图像看作1个信号从中寻找对称的模式,对于包含单一物体或者背景没有太多干扰的图像取得了较好的效果;基于局部特征的方法利用图像中的边缘、轮廓、边界点和局部不变特征通过从特征集合中分组对称特征来寻找对称轴[17-19]。然而唐卡图像构图复杂,包含众多物体(祥云、花卉、法器等),现有的基于全局特征的对称性检测算法在唐卡图像中很难直接使用;而基于局部特征的对称性检测算法得到的潜在具有对称性的特征集合数量太大。事实上在佛像类唐卡中,大多以主尊为中心,四周密密麻麻对称地画出大量繁杂的人物、建筑、山水和花卉等,而在主尊,如佛陀、菩萨、圣者的头顶和身后,都笼罩着一道辉煌的灵光圈,分别称为头光和背光。虽然不同年代的唐卡画像在处理头光、背光图案样式上略有不同,但是头光大多表现为颜色单一、稳定的环形区域。因此,首先将头光区域的范围大致圈定出来,如图2所示,分别显示了佛像绘画中3种具有代表性(发髻、宝冠、僧帽)的头饰特征的结果。
若能检测到图2所示图像的对称轴,则整幅图像的对称轴就可以寻找出来。在唐卡图像绘制的过程中,头光以额际为中心环罩头部,可是额际与佛像人物的面部特征一样,单独提取十分困难;眼睛或眉毛区域相对其他区域的特征较为明显(如图3(a)和图3(c)所示),但是对于头饰为宝冠的一类唐卡,眼睛或眉毛的定位也很复杂(头饰与眼睛、眉毛都为面部复杂度最大的区域,如图3(b)所示)。因此,本文的想法是寻找头光区域,结合文献[20]中的理论提取该区域的对称轴。

图2 唐卡头像的头部区域
Fig. 2 Head regions of Thangka
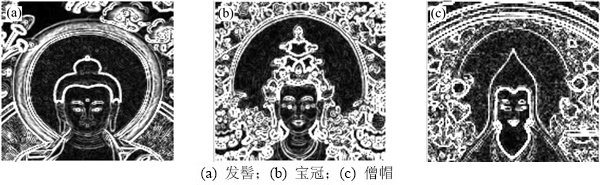
图3 头部区域的边缘
Fig. 3 Edge of head region
以图2(a)为例,将其转化为灰度图像后采用基于划分的聚类算法k-means对其进行分割,设定k=4个初始聚类的种子点,通过计算每个像素点与聚类中心的欧氏距离,选择最近的类别归类,并对聚类中心进行更新,反复迭代直到聚类中心点不再变化为止,最终得到图4(a)所示的分割结果图。鉴于在头部区域中头光部分的颜色稳定,像素点数众多,在最终得到的这k个类中,选择像素点数目最多的颜色稳定性区域,如图4(b)所示。
将头光像素点沿着垂直方向叠加投影,则其函数S(i)为
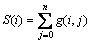 (1)
(1)
式中:n为图像的高度;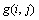 为头光像素点,定义
为头光像素点,定义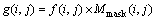 ,
,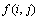 为待处理的头部区域,
为待处理的头部区域,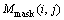 为颜色稳定性区域的二值模板,其对于颜色稳定性区域(图4(b)中光头部分),其值为1,否则值为0。
为颜色稳定性区域的二值模板,其对于颜色稳定性区域(图4(b)中光头部分),其值为1,否则值为0。
式(1)所得的垂直方向投影记为一维函数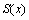 ,对称轴的坐标为xs
,对称轴的坐标为xs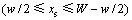 ,其中对称区域的宽度为w,投影后的一维函数的宽度为W,则S(u)是以xs为坐标原点的函数
,其中对称区域的宽度为w,投影后的一维函数的宽度为W,则S(u)是以xs为坐标原点的函数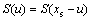 。由于任意函数可以表示为奇函数与偶函数的和,故S(u)的奇函数(o(u))和偶函数(e(u))分量分别为:
。由于任意函数可以表示为奇函数与偶函数的和,故S(u)的奇函数(o(u))和偶函数(e(u))分量分别为:
 (2)
(2)
 (3)
(3)
若偶函数所占比例大,则说明一维函数对称性明显。将偶函数分量归一化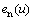 得
得
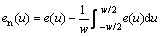 (4)
(4)
因此,对称性测度Ssymmetry可定义为[20]
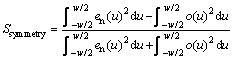 (5)
(5)
当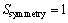 时,完全对称;当
时,完全对称;当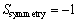 时,完全不对称。实验中,当
时,完全不对称。实验中,当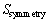 >0.6时就能检测到唐卡图像的对称轴,如图4(c)所示。
>0.6时就能检测到唐卡图像的对称轴,如图4(c)所示。
2.1.2 基于对称性的分块分割
最大类间方差法(OTSU)是1种自适应的阈值确定算法,它按图像的灰度特性,将图像分成背景和目标2个部分。若背景和目标间的类间方差较大,则表明这2部分的差别越大。当部分目标或背景被错分,就会导致这2部分的差别变小。因此,若某个分割阈值使类间方差最大,则意味着该分割错分的概率最小,分割的效果最为理想。本文在图像分块采样的基础上,采用OTSU的方法完成图像分块分割,也避免了当目标所占的比例较小时,图像分割效果不好的缺点。
图5对比显示了基于对称轴的OTSU分块分割和普通的OTSU分块分割的结果图像。由图5可知:本文提出的分块策略分割的结果结合了唐卡图像构图的领域知识,包含的伪破损点少,能更好地表示破损区域。
2.2 多尺度多特征融合的破损分割
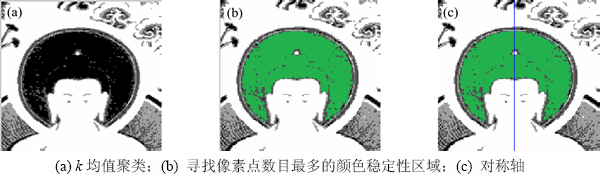
图4 对称轴提取过程
Fig. 4 Extraction process for symmetric axis

图5 基于对称轴的分块分割结果
Fig. 5 Results of block segmentation based on symmetric axis
在完成基于对称轴的分块分割之后,破损区域的全部信息已经包含在背景部分或者物体部分中了,然而在1幅画作中,真实的破损形式众多,特征千差万别,欲获得所有破损区域的模板还必须采用人工辅助的方法。为此,本文针对颜色或纹理特征具有一致性的破损区域进行自动分割。首先利用Gabor滤波器提取图像的纹理特征,Gabor 变换是一种有效的多尺度分析工具,具备分析图像局部细微变化的能力,可以很好地表征唐卡图像中的不同尺度下的纹理。图像Gabor特征可通过将输入图像与Gabor 小波滤波器组卷积得到,即:
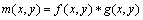 (6)
(6)
式中: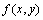 为输入的灰度图像函数;
为输入的灰度图像函数;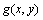 是Gabor滤波函数,定义为:
是Gabor滤波函数,定义为:

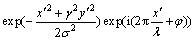 (7)
(7)
 (8)
(8)
式中: 为正弦函数波长;
为正弦函数波长;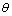 为Gabor核函数的方向;
为Gabor核函数的方向;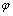 为相位偏移;
为相位偏移; 为高斯函数的标准差;
为高斯函数的标准差; 为空间的宽高比是Gabor 核高斯函数的纵横比,它的范围在0.23~0.92;x和y为给定位置的图像坐标;
为空间的宽高比是Gabor 核高斯函数的纵横比,它的范围在0.23~0.92;x和y为给定位置的图像坐标; 和
和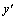 为旋转之后的坐标;i为虚数单位。
为旋转之后的坐标;i为虚数单位。
在提取图像纹理特征时,由于Gabor 响应的幅值信息表征了图像的能量谱,而这种能量谱又是图像局部所具有的,并在图像真实边缘附近具有良好的光滑性,因而可以较好地反映图像的特征,所以进一步计算图像的幅值响应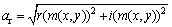 作为最终的图像纹理特征向量ftexture,
作为最终的图像纹理特征向量ftexture,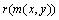 为
为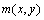 的实部分量,
的实部分量, 为
为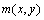 的虚部分量。
的虚部分量。
色彩美是唐卡绘画艺术的一大特色。从色彩运用上:金唐卡以金色为底,上面用黑线勾画;红唐卡以红色为底色;黑唐卡在漆黑的底色上大量勾金;彩唐则以浅蓝、红色、黄色和绿色、金色运用最多。且唐卡色彩分布相对匀称。因此,颜色特征信息的也应该作为提高识别破损区域的特征之一。对于颜色特征的提取,考虑到像素点的颜色差距应该与人眼视觉感觉到的差别相一致,故将RGB空间转换为CIE Lab颜色空间进行处理,具体转换过程为
 (9)
(9)
则CIE Lab空间的亮度L分量,以及有关色彩的a,b分量分别表示为
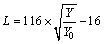 ,
, ,
,
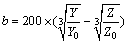 (10)
(10)
其中: 是标准白色的刺激值。通过颜色特征转化得到颜色特征向量
是标准白色的刺激值。通过颜色特征转化得到颜色特征向量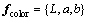 ,最终构成融合纹理特征和颜色特征的特征向量集合
,最终构成融合纹理特征和颜色特征的特征向量集合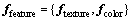 。分类时采用K最近邻分类算法(KNN),通过K个与之最相近的历史记录的组合来辨别新的记录,最终实现破损区域的分割。
。分类时采用K最近邻分类算法(KNN),通过K个与之最相近的历史记录的组合来辨别新的记录,最终实现破损区域的分割。
3 实验和分析
为了验证文中方法的可行性和优越性,采用Matlab编写了相应的实验程序,并与二值化、聚类和文献[10]的分块分割方法进行对比。实验中,参数选择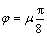 ,
,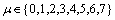 ,
,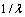 是Gabor 滤波器的中心频率取{0.1,0.3,0.5};参数
是Gabor 滤波器的中心频率取{0.1,0.3,0.5};参数 与滤波器的带宽有关,实验证明当
与滤波器的带宽有关,实验证明当 =0.5时,滤波效果最为理想。
=0.5时,滤波效果最为理想。
图6所示为1幅受到光辐射的影响造成破损的释迦牟尼佛唐卡图像,正中人物从头部、身部横向存在多处颜料的褪色。图6(b)~(d)所示分别为块大小为16像素*16像素的基于对称轴的分块分割、聚类以及二值化分割的结果。由图6(b)~(d)可以看出:本文基于对称轴的分块分割效果最好,这是因为分块分割粒度与其他方法相比较细,因此更好地表征了原始图像中的细节,剔除了未破损点,为后续的再分割奠定了良好的基础。图6(e)所示为分块分割后白色区域覆盖的原始图像,采用本文多尺度多特征的分类算法得到结果图像(如图6(f)所示),利用形态学运算后去除小面积区域后得到结果如图6(h)所示,可以看出结果图像包含了原始图像中的破损区域。
图7所示为1幅由于颜色脱落造成破损的不动佛唐卡图像。首先对比初次分割的效果(如图7(b)~(d)所示)。由图7(b)~(d)可以看出:本文提出的基于对称轴分块分割方法比文献[11]提出的分块分割方法能更好地分割出图像的破损区域,并且误分区域最少。与二值化相比,可以看出在菩萨的面部区域,本文算法取得了最好的效果,同时背景区域的分割也是最大程度地包含了唐卡绘作的祥云部分,因而最有效。在二次分割时,通过多尺度多特征的分类算法挑选出了破损区域,考虑到原始破损图像中由于颜色脱落造成的斑斑点较多,为此不再去除小面积区域,最终得到破损区域的分割结果(如图7(f)所示)。从图7(f)可以看出:本文提出的算法最终包含了原始图像中的斑点状破损。然而,由于佛像人物身部出现的水平方向的折痕与斑点状破损从视觉表现上有很大的不同,因此在二次分割时,算法没能很好地对其刻画。

图6 唐卡1图像破损区域分割结果
Fig. 6 Result of damaged regions segmentation of Thangka 1
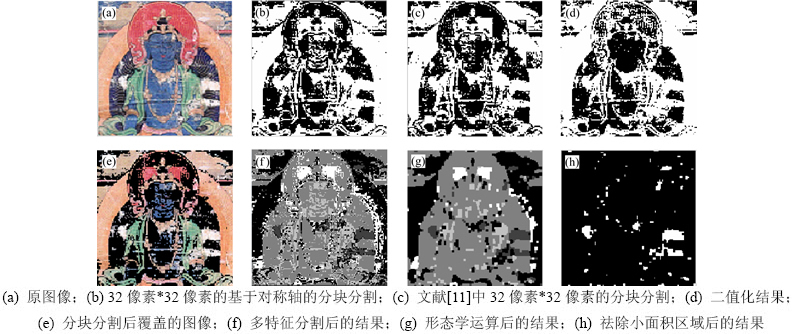
图7 唐卡2图像破损区域分割结果
Fig. 7 Result of damaged regions segmentation of Thangka 2
此外,在具体分割实验中,模板大小的最佳取值,可以采用不同的模板分别进行实验,并从中寻找效果最好的值得到。当然也应结合一些经验:若模板太小,则分割结果过于精细,包含的伪破损潜在区域太多,不利用后续分割;若模板太大,则忽略了对称性。
4 结论
1) 本文提出的算法对于部分佛像类破损唐卡图像破损区域的自动分割取得了较好的效果。
2) 在1幅唐卡画作中,由于物理或人为的原因导致了多种不同类型的破损形式可能同时出现,损毁原因不同,破损形式不同,从图像处理角度采用的破损区域分割算法就不尽相同。此外,由于唐卡图像内容丰富,从视觉上区分破损区域和非破损区域还有一定困难,因此,需研究一种集成的能分割多种破损形式的破损区域分割算法。
参考文献:
[1] 胡文瑾, 李战明, 刘仲民. 快速的非局部均值形态成分分析唐卡图像修复算法[J]. 计算机辅助设计与图形学学报, 2014, 26(7): 1067-1074.
HU Wenjin, LI Zhanming, LIU Zhongmin. Fast morphological component analysis Thangka image inpainting based on nonlocal mean filter[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(7): 1067-1074.
[2] LIU Y, CASELLES V. Exemplar-based image inpainting using multiscale graph cuts[J]. IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2013, 22(5): 1699-1711.
[3] WANG Jing, LU Ke, PAN Daru, et al. Robust object removal with an exemplar-based image inpainting approach[J]. Neurocomputing, 2014, 123: 150-155.
[4] 徐胜军, 韩九强, 何波, 等. 融合边缘特征的马尔可夫随机场模型及分割算法[J]. 西安交通大学学报, 2014, 48(2): 14-19.
XU Shengjun, HAN Jiuqiang, HE Bo, et al. A region Markov random field model with integrated edge feature and image segmentation algorithm[J]. Journal of Xi’an Jiaotong University, 2014, 48(2): 14-19.
[5] 李传龙, 李颖, 刘爱莲. 灰度不均匀图像分割[J]. 大连理工大学学报, 2014, 54(1): 106-114.
LI Chuanlong, LI Ying, LIU Ailian. Segmentation of image with intensity inhomogeneity[J]. Journal of Dalian University of Technology, 2014, 54(1): 106-114.
[6] 张泽均, 水鹏朗. 边缘惩罚层次区域合并SAR图像分割算法[J]. 电子与信息学报, 2015, 37(2): 261-267.
ZHANG Zejun, SHUI Penglang. SAR image segmentation algorithm using hierarchical region merging with edge penalty[J]. Journal of Electronics & Information Technology, 2015, 37(2): 261-267.
[7] 曹家梓, 宋爱国. 基于马尔科夫随机场的纹理图像分割方法研究[J]. 仪器仪表学报, 2015, 36(4): 776-786.
CAO Jiazi, SONG Aiguo. Research on the texture image segmentation method based on Markov random field[J]. Chinese Journal of Scientific Instrument, 2015, 36(4): 776-786.
[8] 许新征, 丁世飞, 史忠植, 等. 图像分割的新理论和新方法[J]. 电子学报, 2010, 38(2): 76-82.
XU Xinzheng, DING Shifei, SHI Zhongzhi, et al. New theories and methods of image segmentation[J]. Acta Electronica Sinica, 2010, 38(2): 76-82.
[9] 胡文瑾, 李战明, 刘仲民. 一种基于小波分析的唐卡图像划痕检测[J]. 光学技术, 2012, 38(6): 751-755.
HU Wenjin, LI Zhanming, LIU Zhongmin. A vertical scratch detection algorithm based on wavelet analysis for Thangka image[J]. Optical Technique, 2012, 38(6): 751-755.
[10] 刘华明, 毕学慧. 唐卡褪色区域分割[J]. 计算机辅助设计与图形学学报, 2013, 25(2): 1-8.
LIU Huaming, BI Xuehui. Segmentation of faded regions in Thangka images[J]. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(2): 1-8.
[11] 关却呼尼玛. 唐卡绘画艺术的审美特征[J]. 西藏艺术研究, 2009(3): 25-31.
DKONMCHOG Sgrolma. The aesthetic characteristics of the Thangka painting[J]. Tibetan Art Studies, 2009(3): 25-31.
[12] 姜允志, 郝志峰, 林志勇, 等. 基于分块采样和遗传算法的自动多阈值图像分割[J]. 计算机辅助设计与图形学学报, 2011, 23(11): 1860-1868.
JIANG Yunzhi, HAO Zhifeng, LIN Zhiyong, et al. Automatic multilevel sampling and genetic thresholding for image segmentation based on block algorithm[J]. Journal of Computer-Aided Design & Computer Graphics, 2011, 23(11): 1860-1868.
[13] 朱立新, 夏德深. 目标自适应图像分块与小目标提取[J]. 计算机工程与应用, 2006, 41(25): 88-90.
ZHU Lixin, XIA Deshen. Object adaptive image division and object extraction[J]. Computer Engineering and Applications, 2006, 41(25): 88-90.
[14] 肖志涛, 史文静, 耿磊, 等. 基于相位信息和主成分分析的对称性检测方法[J]. 电子与信息学报, 2014, 36(9): 2041-2046.
XIAO Zhitao, SHI Wenjing, GENG Lei, et al. Symmetry detection based on phase information and principal component analysis[J]. Journal of Electronics & Information Technology, 2014, 36(9): 2041-2046.
[15] LEE S, LIU Y X. Skewed rotation symmetry group detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1659-1672.
[16] KELLER Y, SHKOLNISKY Y. An algebraic approach to symmetry detection[C]// Proceedings of the 17th International Conference on Pattern Recognition. Cambridge, UK: IEEE Computer Society, 2004: 186-189.
[17] CICCONET M, GEIGER D, GUNSALUS K C, et al. Mirror symmetry histograms for capturing geometric properties in images[C]// Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Columbus, USA: IEEE Computer Society, 2014: 2981-2986.
[18] PATRAUCEAN V, VON-GIOI R G, OVSJANIKOV M. Detection of mirror-symmetric image patches[C]// 2013 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Portland, Oregon, USA: IEEE Computer Society, 2013: 211-216.
[19] LEE S, LIU Y X. Curved glide-reflection symmetry detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(2): 266-278.
[20] ZIELKE T, BRAUCKMANN M, SEELEN W V. Intensity and edge-based symmetry detection applied to car-following[J]. Lecture Notes in Computer Science, 1992, 588(12): 865-873.
(编辑 刘锦伟)
收稿日期:2015-07-03;修回日期:2015-09-15
基金项目(Foundation item):国家自然科学基金资助项目(61561042);中央高校基本科研业务费专项资金项目(31920150082) (Project(61561042) supported by the National Natural Science Foundation of China; Project(31920150082) supported by the Fundamental Research Funds for the Central Universities)
通信作者:胡文瑾,博士,从事图像修复、图像分割等研究;E-mail: wenjin_zhm@126.com