J. Cent. South Univ. Technol. (2010) 17: 621-627
DOI: 10.1007/s11771-010-0531-3 
Influences of strain softening and seepage on elastic and plastic solutions of circular openings in nonlinear rock masses
YANG Xiao-li(杨小礼), HUANG Fu(黄阜)
School of Civil and Architectural Engineering, Central South University, Changsha 410075, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: Considering the influence of strain softening, the solutions of stress, displacement, plastic softening region radius and plastic residual region radius were derived for circular openings in nonlinear rock masses subjected to seepage. The radial stress distribution curve, ground reaction curve, and relation curve between plastic softening region radius and supporting force in three different conditions were drawn respectively. From the comparisons among these results for different conditions, it is found that when the supporting force is the same, the displacement of tunnel wall considering both seepage and strain softening is 85.71% greater than that only considering seepage. The increase values of radial displacement at 0.95 m and plastic softening region radius at 6.6 m show that the seepage and strain softening have the most unfavorable effects on circular opening stability in strain softening rock masses.
Key words: strain softening; seepage; nonlinear yield; ground reaction curve; rock masses
1 Introduction
Analysis of stress and strain around circular opening excavated in isotropic rock masses is one of the classical problems in rock mechanics. At present, Fenner formula is widely used in elastoplastic analysis for rock masses around circular opening. However, Fenner formula is based on elastic-perfectly plastic model, which does not accord to the stress-strain property of actual rock masses, especially to the strain softening and nonlinearity. There is a significant strain softening phenomenon after these rock materials reached the peak value under external force, and these materials show the elastic-softening- residual property [1-4]. For circular openings in the softening materials, there may be three stress regions such as elastic region, plastic softening region and plastic residual region. According to this division, several calculation methods and models considering strain softening have been presented [5-7]. These documents all adopt the linear Mohr-Coulomb (MC) yield criterion. However, evidence shows that nonlinear yield criterion is able to represent satisfactorily the yield of almost all types of rock masses, and that the strength envelope of rock masses is nonlinear [8-12]. A bilinear envelope was used to approximate the nonlinear yield criterion. A piece wise linear approximation was presented to nonlinear yield criterion. This departure from linearity is significant for the stress and displacement calculations of circular openings. So nonlinear yield criterion is used in elastoplastic calculations for circular openings in strain softening rock masses where the seepage influence is not considered [13-14]. For example, based on the nonlinear Hoek-Brown (HB) yield criterion and taking account of effects of elastic strain increments and variable dilatancy in the plastic region, a simple procedure for the ground response curve of a circular opening excavated in strain softening rock masses is presented. The effects of variable dilatancy and peak dilatancy angle on the ground response curve are investigated for circular openings in poor quality rock masses. The result shows a very good agreement with the closed-form solution for the brittle-plastic and strain-softening cases.
The above elastoplastic calculations of circular openings with strain softening do not take account of the influence of underground water seepage. However, underground water is one of the environmental factors for rock masses, and seepage field constantly affects displacement field and stress field around the under- ground opening. For opening structure deeply buried in water-rich rock masses or bearing high hydraulic pressure, the influence of seepage force on surrounding stress and displacement fields will reach a point that cannot be ignored. Based on linear MC yield criterion and taking account of the seepage force, CAI and HE [15] derived simplified analytical solutions of stress and displacement distribution around circular opening, with the seepage being steady-state flow. Assuming the influence factors surrounding deep-buried circular opening are axially symmetrical and the seepage force is body force, RONG and CHENG [16] and LI et al [17] derived analytical formulae of plastic stress and plastic radius around circular opening with linear MC yield criterion. In Refs.[15-17], the influences of nonlinear yield criterion and strain softening property are not considered.
Until now, all the strain softening analysis for rock masses around circular opening based on nonlinear yield criterion has not taken account of the influence of seepage effect, while the documents considering seepage effect are all based on MC linear yield criterion. Consequently, a question, which arises in practice and theoretical study, is how to study the problem of circular openings subjected to seepage force when the circular openings are in strain softening rock masses with nonlinear yield criterion. Considering the influences of seepage force and strain softening on rock masses around circular openings, the analytical solutions of stress and displacement are derived for elastic region, plastic softening region and plastic residual region with nonlinear HB yield criterion. The present results are compared with previously published solutions. Since water flow inside porous rock masses may affect the effective stresses on the rock skeleton, it is the effective stress that should be used in the following analysis.
2 Problem description
2.1 Yield criterion with strain softening
The empirical formula on determining the strength of rock masses proposed by HOEK and BROWN [18] in 1980 for the first time has been widely used in rock mechanics since the modification. The nonlinear HB yield criterion is written as
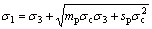 (ε<ε1e) (1a)
(ε<ε1e) (1a)
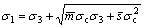 (ε1e<ε<αε1e) (1b)
(ε1e<ε<αε1e) (1b)
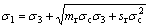 (αε1e<ε) (1c)
(αε1e<ε) (1c)
where σ1 and σ3 are the maximum principal stress and the minimum principal stress, respectively; σc is the uniaxial compressive strength of the intact rock material; mp, sp, 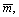
 and mr, sr are the material parameters that depend on the properties of the rock masses, corresponding to the peak, softening and residual values of HB criterion for the yielded rock, respectively; α is the softening factor defining strain at which residual strength is reached; ε1e is the maximum principal elastic strain component at the interface between the elastic region and the plastic softening region; and αε1e is the maximum principal strain component at the interface between the plastic softening region and the plastic residual region (see Fig.1, where
and mr, sr are the material parameters that depend on the properties of the rock masses, corresponding to the peak, softening and residual values of HB criterion for the yielded rock, respectively; α is the softening factor defining strain at which residual strength is reached; ε1e is the maximum principal elastic strain component at the interface between the elastic region and the plastic softening region; and αε1e is the maximum principal strain component at the interface between the plastic softening region and the plastic residual region (see Fig.1, where 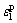 is the maximum principal strain in plastic region; and
is the maximum principal strain in plastic region; and 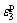 is the minimum principal strain in plastic region).
is the minimum principal strain in plastic region).
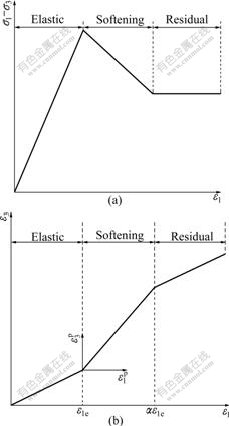
Fig.1 Elastic-softening-residual model: (a) Stress relations; (b) Strain relations
For circular openings in polar coordinate system, the circumferential stress and strain are the major principal stress and strain, respectively. Both 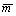 and
and  were assumed to decrease linearly with strain from their peak values, mp and sp, at εθ=εθe to the residual ones, mr and sr, at εθ=εθe. The formulae take the form by
were assumed to decrease linearly with strain from their peak values, mp and sp, at εθ=εθe to the residual ones, mr and sr, at εθ=εθe. The formulae take the form by
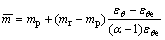 (2a)
(2a)
 (2b)
(2b)
where εθe is the circumferential elastic strain at the interface between the elastic region and the plastic softening region.
2.2 Assumptions
It is assumed that there is a circular opening in infinite elastic medium, as shown in Fig.2, where a is the initial radius of the circular opening, b is the radius of elastic region, R is the radius of plastic softening region, and pw is the internal supporting force of circular opening wall. As pw is gradually reduced, the radial displacement occurs, and no plastic region emerges. With force pw continuing to decrease, the radial stress and circumferential stress vary gradually until Eq.(1) is satisfied, and a plastic region is produced around the circular opening. Then, elastic region, plastic softening region and plastic residual region form. In order to study qualitatively the seepage force effect on stress and displacement around the circular opening in strain softening rock masses, several assumptions have been proposed as follows. The rock masses around the circular opening are regarded as isotropic continuous permeability media. The hydrostatic pressure in seepage field is assumed to distribute uniformly in radial direction and to equal each other at the same radius. The rock masses around the circular opening follow the nonlinear HB yield criterion, and the calculation process obeys plane strain assumption. Supporting force pw on excavation face is distributed uniformly in radial direction.
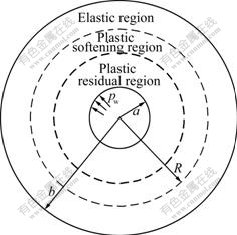
Fig.2 Description of three regions around circular opening
3 Solutions of stress and displacement with seepage
3.1 Seepage field
The radial seepage force Fr is assumed to be the same in all directions around the circular opening in infinite medium, and the seepage direction is mainly radial. Therefore, the issue of seepage involved is regarded as an issue of axisymmetric steady-state flow condition. According to underground water continuity equation and Darcy law, radial seepage force which is produced by underground water flowing could be determined by the form [17]:
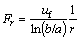 (3)
(3)
where uf is the hydrostatic pressure in seepage field; and r is the radial distance from the centre of circular opening.
3.2 Stress and displacement distribution in elastic region
In the elastic region, due to the assumption that linear elastic material exits outside the plastic region, general expressions for the radial and circumferential stresses can be obtained from the theory of elasticity, as shown in Ref.[16], which are
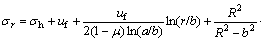
 (4a)
(4a)

 (4b)
(4b)
where σh is the hydrostatic stress; μ is Poisson ratio; and σR is the radial stress at the corresponding interface. For 2D plane strain problem, the equilibrium equation with seepage is written as [16]
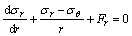 (5)
(5)
Substituting Eq.(3) and Eq.(1a) into Eq.(5), the differential function at the initial yield interface is obtained when the elastic region is transformed into plastic softening region
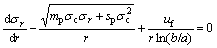 (6)
(6)
Eq.(6) has two integral variables. Integrating Eq.(6) will lead to
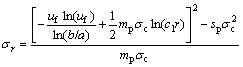 (7)
(7)
where c1 is the integral constant, and it can be determined by the boundary condition  Substituting the boundary condition into Eq.(7), integral constant c1 is determined. The radial stress at the interface between the elastic region and the plastic softening region is
Substituting the boundary condition into Eq.(7), integral constant c1 is determined. The radial stress at the interface between the elastic region and the plastic softening region is
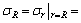
 (8)
(8)
Substituting Eq.(8) into Eq.(4), the radial and circumferential stresses in the elastic region around the circular opening with the consideration of seepage force are obtained.
As mentioned above, RONG and CHENG [16] derived the analytical expressions of stress and displacement around circular openings with linear MC yield criterion, considering the influence of seepage force. Seepage, strain softening and nonlinear yield criterion are taken into account in the present analysis. However, the radial displacement distribution of the present study in the elastic region is the same as the expression calculated by RONG and CHENG [16], which is
 (9)
(9)
where


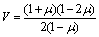
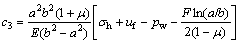
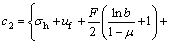
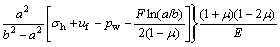 (10)
(10)
3.3 Stress and displacement distribution in plastic softening region
For a 2D plane strain axisymmetric problem, the compatible conditions in plastic softening region can be expressed as 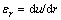 and
and 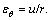 Since the volumetric strain in plastic softening region is zero i.e.,
Since the volumetric strain in plastic softening region is zero i.e.,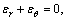 the equation of
the equation of 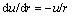 is obtained. Integrating the equation, radial displacement
is obtained. Integrating the equation, radial displacement  in the plastic softening region is written as
in the plastic softening region is written as
 (11)
(11)
where Ap is the integral constant. According to the displacement continuous condition at the interface between the elastic region and the plastic softening region  Eq.(11) can be solved. Since
Eq.(11) can be solved. Since 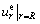 is determined by Eq.(9), coefficient Ap takes form by
is determined by Eq.(9), coefficient Ap takes form by
 (12)
(12)
The displacement of plastic softening region can be written as
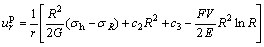 (13)
(13)
According to the compatible condition 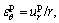 the expression for circumferential strain in plastic softening region can be written as
the expression for circumferential strain in plastic softening region can be written as
 (14)
(14)
The circumferential strain at the interface between the elastic region and the plastic softening region is thus determined by substituting the condition r=R into Eq.(14), which is
 (15)
(15)
Substituting Eqs.(14) and (17) into Eq.(2), the following expressions are obtained
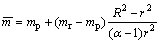 (16)
(16)
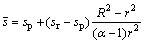 (17)
(17)
In the softening region, the yield of rock masses follows Eq.(1b). Substituting Eqs.(16) and (17) into Eq.(1b), the yield criterion in plastic strain softening region is written as

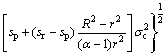 (18)
(18)
Substituting Eq.(18) into equilibrium Eq.(5), a first order nonlinear differential equation may be obtained

 (19)
(19)
Since Eq.(19) is a nonlinear differential equation, the analytical solution cannot be found. In present analysis, the numerical solution of radial stress around circular opening is obtained by numerical technique, and the results are shown in Fig.3 for rock masses with poor quality. The parameters for poor quality of rock masses are mp=1.7, sp=0.003 9, mr=0.85, sr=0.001 9 and σc= 30 MPa. From Fig.3, it is found that the radial stress in the plastic residual region increases with increasing the ratio of r/a. Except for the special explanation, these parameters are used in the following analysis.
3.4 Stress and displacement distribution in plastic residual region
Employing the assumption that the volumetric strain in plastic residual region is also zero, i.e., 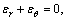 the expression
the expression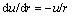 is obtained from the
is obtained from the
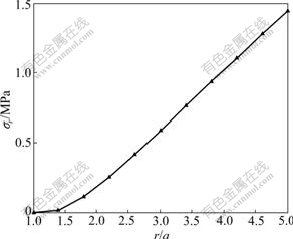
Fig.3 Numerical solutions of σr for rock masses with poor quality
compatible conditions. Based on the displacement continuity condition  at r=tR, where t is the ratio of the radius of plastic residual region to the radius of plastic softening region, integrating the equation du/dr=-u/r, radial displacement
at r=tR, where t is the ratio of the radius of plastic residual region to the radius of plastic softening region, integrating the equation du/dr=-u/r, radial displacement 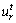 in the plastic residual region is written as
in the plastic residual region is written as
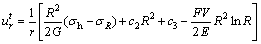 (20)
(20)
Based on Eq.(1c), the yield of plastic residual region in polar coordinate system is written as
 (21)
(21)
Substituting Eq.(21) into equilibrium Eq.(5), then integrating the expression, the stress of plastic residual region is written as
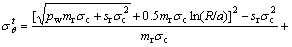
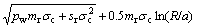 (22)
(22)
3.5 Radii of plastic residual region and plastic softening region
At the interface between the plastic softening region and the plastic residual region, the values of rock parameters 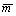 and
and  are equal to the values of mr and sr, respectively. Therefore, the expressions of
are equal to the values of mr and sr, respectively. Therefore, the expressions of  and
and  are obtained. Substituting Eqs.(16) and (17) into the expressions of
are obtained. Substituting Eqs.(16) and (17) into the expressions of 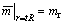 and
and  will lead to
will lead to 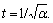 According to equilibrium equations and boundary condition r=R, the function at the interface between the elastic region and the plastic softening region is obtained. The radius of plastic softening region is obtained.
According to equilibrium equations and boundary condition r=R, the function at the interface between the elastic region and the plastic softening region is obtained. The radius of plastic softening region is obtained.
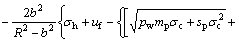
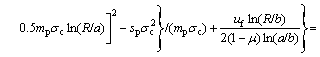
 (23)
(23)
Eq.(23) can be solved to obtain the magnitude of the radius of plastic softening region. Then, the radius of plastic residual region is equal to tR.
4 Results and discussion
Numerical results are obtained for the circular opening with initial radius a=5 m, seepage pressure uf=1.05 MPa, softening factor α=2, and hydrostatic stress σh=2.73 MPa. Rock masses with poor quality, are adopted in the present analysis. These results are summarized in Figs.4-6. Example problems are selected to include the following issues: (1) comparisons are made between the present results and the previously published solutions, and (2) effects of seepage force and strain softening on the displacement and stress of circular opening are studied.
4.1 Radial stresses for different situations
Fig.4 illustrates the three curves of radial stress distributions in three different conditions: (1) taking account of seepage and strain softening, (2) only taking account of strain softening and (3) without considering strain softening and seepage. The curve of the present study is drawn based on the formula taking account of seepage and strain softening. Furthermore, the results of BROWN et al [19] only taking account of strain softening and solutions of WANG [20] without considering strain softening are drawn in Fig.4. The purpose of this comparison is to examine the effect of seepage and strain softening for the distribution of radial stress.
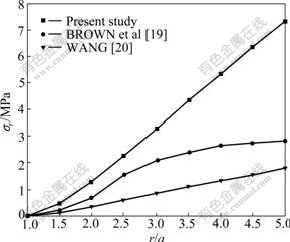
Fig.4 Comparison of radial stress σr distribution for three different situations
It can be seen from Fig.4 that, when the radius of the circular opening is the same, the radial stress with the consideration of both seepage and strain softening is significantly larger than that of either: only considering strain softening or without considering both. By comparing the results among present study, BROWN et al [19] and WANG [20], it is found that the difference between the results of present study and BROWN et al [19] is much larger than the difference between the results of BROWN et al [19] and WANG [20], especially in the region away from the circular opening wall. Thus, the effect of seepage is much greater than the strain softening for radial stress around circular openings [21].
4.2 Ground reaction curves for different situations
Based on the nonlinear HB yield criterion, the differences of ground reaction curves are compared in three different conditions: (1) taking account of seepage and strain softening, (2) only taking account of seepage and (3) without considering both. The ground reaction curves are illustrated in Fig.5, where the abscissa ur is the radial displacement of circular opening wall. Without taking account of seepage and strain softening, the ground reaction curve is drawn according to the formula derived by WANG [20]. From Fig.5, it is found that when the supporting force is the same, the displacement with the consideration of both seepage and strain softening is significantly larger than that of either: only considering seepage or without considering both. For example, with the supporting force pw=0.5 MPa, the displacement of without considering both is 0.37 cm, less than that of others. Therefore, the condition of considering seepage and strain softening at the same time is the most unfavorable to the stability of circular opening.
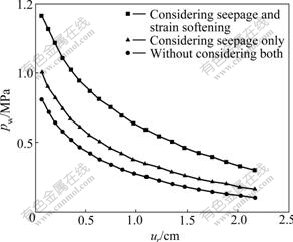
Fig.5 Ground response curves for different situations
4.3 Plastic softening region radius for different situations
Fig.6 shows the relationship curves between the plastic softening region radius and the supporting force of circular opening in three different conditions: (1) considering seepage and strain softening, (2) only considering seepage and (3) without considering strain softening and seepage. For example, with the supporting force pw=6 MPa, the value of the plastic softening region radius is R=6.25 m for the case without considering both, is R=7.53 m for considering seepage only, and is R= 13.20 m for considering both. Therefore, with the same supporting force, the radius of plastic softening region considering seepage and strain softening is much greater than the radius of plastic softening region only considering seepage or without considering both.
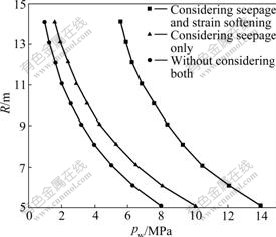
Fig.6 Relationship curves between plastic softening radius R and pw for different situations
5 Conclusions
(1) Based on the nonlinear HB yield criterion, the analytical solutions are derived for stress, displacement and radii in plastic softening region and plastic residual region for circular openings in strain softening rock masses, with taking into account of seepage force. The curves of radial stress, ground reaction curve, relation curve between radius of plastic softening region and supporting force are drawn for engineering practice.
(2) According to the derived analytical solutions, the influences of seepage on the radial stress and displacement around circular opening in strain softening rock masses are investigated by comparing the present results with previously published solutions. From the comparison, it is found that the effect of seepage is much larger than that of strain softening.
(3) According to the curves of radial stress, ground reaction curve, relation curve between radius of plastic softening region and supporting force, it is found that the seepage has unfavorable influence on the stability of circular openings in strain softening rock masses.
References
[1] ALKAN H. Percolation model for dilatancy-induced permeability of the excavation damaged zone in rock salt [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 716-724.
[2] CONTE E, COSENTINI R M, TRONCONE A. Shear and dilatational wave velocities for unsaturated soils [J]. Soil Dynamics and Earthquake Engineering, 2009, 29(6): 946-952.
[3] EGGER P. Design and construction aspects of deep tunnels with particular emphasis on strain softening rocks [J]. Tunnelling and Underground Space Technology, 2008, 23(4): 403-408.
[4] PAN Y S, WANG X B, LI Z H. Analysis of the strain softening size effect for rock specimens based on shear strain gradient plasticity theory [J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(6): 801-805.
[5] ALONSO E, ALEJANO L R, VARAS F, FDEZ-MANIN G, CARRANZA-TORRES C. Ground response curves for rock masses exhibiting strain softening behavior [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(13): 1153-1185.
[6] CORTHESY R, LEITE M H. A strain-softening numerical model of core discing and damage [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(3): 329-350.
[7] VARAS F, ALONSO E, ALEJANO LR, FDEZ-MANIN G. Study of bifurcation in the problem of unloading a circular excavation in a strain-softening material [J]. Tunnelling and Underground Space Technology, 2005, 20(4): 311-322.
[8] HOEK E, CARRANZA-TORRES C, CORKUM B. Hoek-Brown failure criterion—2002 edition [C]// Proceedings of the North American Rock Mechanics Society Meeting. Toronto, 2002: 267-273.
[9] YANG Xiao-li, HUANG Fu. Slope stability analysis considering joined influences of nonlinearity and dilation [J]. Journal of Central South University of Technology, 2009, 16(2): 292-296.
[10] CAI M, KAISER P K, TASAKA Y, MINAMI M. Determination of residual strength of jointed rock masses using the GSI system [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(2): 247-265.
[11] CAI M. Influence of intermediate principal stress on rock fracturing and strength near excavation boundaries-Insight from numerical modeling [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 763-772.
[12] YANG Xiao-li. Seismic bearing capacity of a strip footing on rock slopes [J]. Canadian Geotechnical Journal, 2009, 46(8): 943-954.
[13] YANG Xiao-li. Seismic displacement of rock slopes with nonlinear Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 948-953.
[14] BAKER R. Inter-relations between experimental and computational aspects of slope stability analysis [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(5): 379-401.
[15] CAI Mei-feng, HE Man-chao, LIU Dong-yan. Rock mechanics and engineering [M]. Beijing: Science Press, 2006: 307-326. (in Chinese)
[16] RONG Chuan-xin, CHENG Hua. Stability analysis of rocks around tunnel with ground water permeation [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 741-744. (in Chinese)
[17] LI Zong-li, REN Qing-wen, WANG Ya-hong. Elasto-plastic analytical solution of deep-circle tunnel considering fluid flow field [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1291-1295. (in Chinese)
[18] HOEK E, BROWN E T. Empirical strength criterion for rock masses [J]. Journal of Geotechnical Engineering Division, ASCE, 1980, 106(9): 1013-1035.
[19] BROWN E T, BRAY J W, LADANYI B, HOEK E. Ground response curves for rock tunnels [J]. Journal of Geotechnical Engineering, 1983, 109(1): 15-39.
[20] WANG Y. Ground response of circular tunnel in poorly consolidated rock [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1996, 122(9): 703-708.
[21] YANG Xiao-li, YIN Jian-hua. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267-273.
Foundation item: Project(09JJ1008) supported by Hunan Provincial Science Foundation of China; Project(200550) supported by the Foundation for the Author of National Excellent Doctoral Dissertation of China
Received date: 2009-09-07; Accepted date: 2009-12-08
Corresponding author: YANG Xiao-li, Professor; Tel: +86–731–82656248; E-mail: yxnc@yahoo.com.cn
(Edited by YANG You-ping)