The governing Eqs. (1)–(4) can be expressed in component form as below [2, 16]:
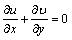 (5)
(5)
 (6)
(6)
 (7)
(7)
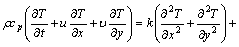
 (8)
(8)
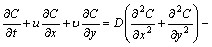
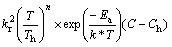 (9)
(9)
where u and υ are velocity components along x and y direction, respectively; v is kinematics viscosity and σ* is electrical conductivity.
The differences in temperature inside fluid flow are poor enough, so that the function Tn can be expressed linearly. Tn can be expanded utilizing Taylor’s series in respect of temperature Th by neglecting higher order terms which results in the approximation given below:
 (10)
(10)
The boundary conditions are illustrated below:
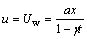 , υ=0, T=Tw, C=Cw at y=0, u=0,
, υ=0, T=Tw, C=Cw at y=0, u=0,
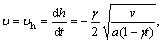 T=Th, C=Ch at y=h(t) (11)
T=Th, C=Ch at y=h(t) (11)
where a, γ, Tw, Cw, Th and Ch represent stretching rate, unit free constant, temperature at surface, particle concentration at surface, temperature at upper plate and particle concentration at upper plate respectively.
In order to evaluate the constitutive Eqs. (5)– (10) with subjected boundary conditions (11), we utilize the well-defined non-dimensional variables:


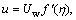
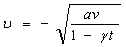 ,
, 
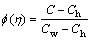 (12)
(12)
Eliminating pressure term from Eqs. (6)–(7) and in view of Eq. (12), the above governing equations assume the following form:
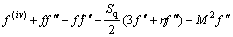 (13)
(13)

 (14)
(14)

 (15)
(15)
where Sq=γ/a is squeezing parameter. The value of Sq<0 corresponds to away movement of the plates; Sq>0 indicates that the plates move towards each other, while Sq=0 is relative to steady case or stationary plate.
The other involved parameters are expressed below. Magnetic parameter M2, Prandtl number Pr, non-dimensional exothermic/endothermic parameter λ, dimensionless reaction rate σ, temperature difference parameter γ1, non- dimensional activation energy parameter E and Schmidt number Sc

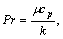




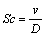 (16)
(16)
The prescribed dimensionless boundary conditions are defined below
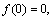
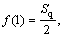
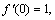
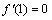 ,
, 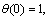
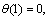
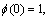
 (17)
(17)
Define skin friction co-efficient, Nusselt and Sherwood numbers as
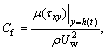
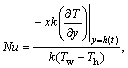
 (18)
(18)
In view of Eq. (12), Eq. (18) takes the form:
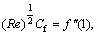
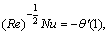
 (19)
(19)
3 Series solutions
In this portion, the homotopic technique (HAM) proposed by LIAO [28, 29] is utilized to evaluate the non-linear governing ODEs Eqs. (13)– (15) with subjected boundary conditions Eq. (17). In this technique, initial guesses and linear operators are utilized to acquire the convergent series solution. Recently this approach has been successfully employed to simulate many multi-physical transport phenomena including flow of stagnant fluid (HAYAT et al [30]), Newtonian heat transfer (HAYAT et al [31]), magneto-hydrodynamics with radiative heat transfer (FAROOQ et al [32]), MHD flow of stratified nanoliquid (WAQAS et al [33]), radiative flow of squeezed fluid with transport of convective heating (HAYAT et al [34]), magneto fluid flow over radiating exponentially stretched surface (MABOOD et al [35]), magnet- hydrodynamic stagnant flow over variable thicked surface saturated in stratified medium (FAROOQ et al [36]) and chemically reactive nanomaterial flow with heat source (HAYAT et al [37]).For the implementation of this method we select initial guesses and linear operators as below:
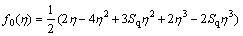 (20)
(20)
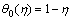 (21)
(21)
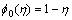 (22)
(22)
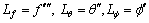 (23)
(23)
with
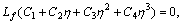
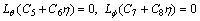 (24)
(24)
where Ci (i=1, 2, …, 8) are arbitrary constants.
3.1 Zeroth-order problems
Here,
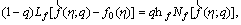
 (25)
(25)
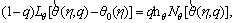
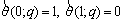 (26)
(26)
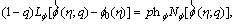
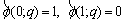 (27)
(27)
Define non-linear operators as:


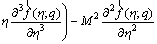 (28)
(28)
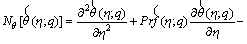
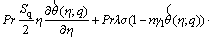
 (29)
(29)
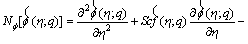
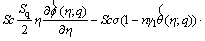
 (30)
(30)
where 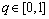 is embedding parameter and auxiliary non-zero parameters are
is embedding parameter and auxiliary non-zero parameters are 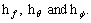
3.2 The mth-order problems
Here
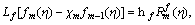
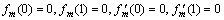 (31)
(31)
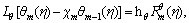
 (32)
(32)
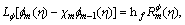
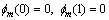 (33)
(33)
Define non-linear operators as follows:
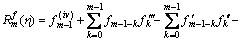
 (34)
(34)
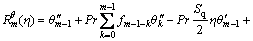

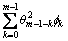 (35)
(35)


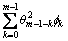 (36)
(36)
 (37)
(37)
For q=0 and q=1, we can write
 (38)
(38)
and with the variation of q from 0 to 1, 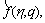
 and
and 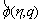 vary from the initial solutions f0(η), θ0(η) and f0(η) to the final solutions f(η), θ(η) and f(η), respectively. By Taylor series, we have
vary from the initial solutions f0(η), θ0(η) and f0(η) to the final solutions f(η), θ(η) and f(η), respectively. By Taylor series, we have


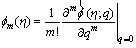 (39)
(39)
Choose suitable value for auxiliary parameter that the series Eq. (39) converges at q=1, i.e.,
 (40)
(40)
where fm, θm and fm represent general solutions for Eqs. (31)–(33) in the form of special solutions 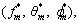 given by
given by
 (41)
(41)
3.3 Convergence of problem
Here series solutions Eq. (36) contain non-zero auxiliary parameters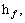
 and
and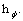 These parameters have valuable role in controlling convergence of solution expressions. The convergence of the results is displayed in Figure 2. It is noticed that series solutions convergences are in the regions
These parameters have valuable role in controlling convergence of solution expressions. The convergence of the results is displayed in Figure 2. It is noticed that series solutions convergences are in the regions  and
and 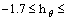 –0.1 and
–0.1 and  Moreover, Table 1 exhibits the convergent series solutions which ensure the graphical results depicted in Figure 1. It is noticed that the 7th order of approximations is enough for series solutions convergence.
Moreover, Table 1 exhibits the convergent series solutions which ensure the graphical results depicted in Figure 1. It is noticed that the 7th order of approximations is enough for series solutions convergence.
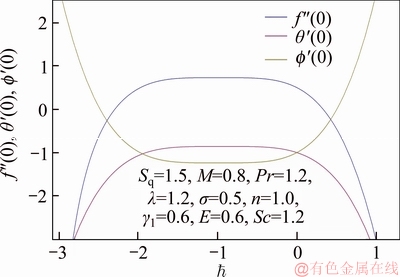
Figure 2 Convergence region for f(η), θ(η) and f(η)
4 Results and interpretation
The parameters existing in considered flow analysis are squeezing parameter Sq, magnetic parameter M, Prandtl number Pr, non-dimensional exothermic/endothermic parameter λ, temperature difference parameter γ1, dimensionless reaction rate σ, non-dimensional activation energy parameter E and Schmidt number Sc.
Table 1 Convergence of homotopy solutions for different orders of approximation when Sq=1.5, M=0.8, Pr=1.2, λ=1.2, σ=0.5, n=1.0, γ1=0.6, E=0.6, Sc=1.2
Therefore, in this segment, the characteristics of each of them have been analyzed when the others are treated constant. Thus the results are provided in the form of flow velocity field, temperature and fluid concentration distribution in Figures 3–17 for the variation of Sq, M, Pr, λ, σ, γ1, E and Sc.
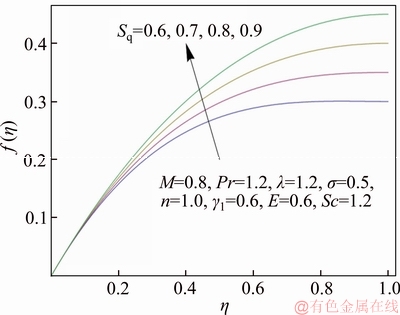
Figure 3 Variation of Sq on f(η)
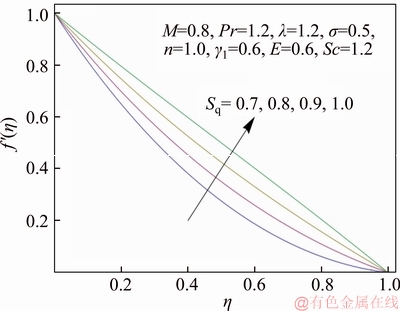
Figure 4 Variation of Sq on f ′(η)
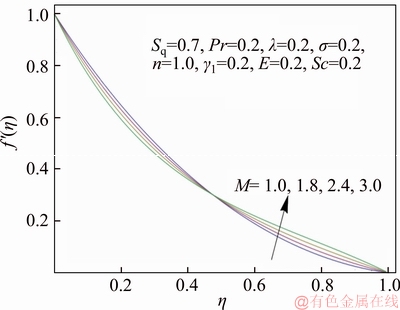
Figure 5 Variation of M on f ′(η)
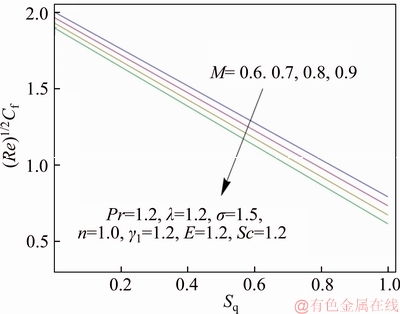
Figure 6 Variation of M and Sq on Cf
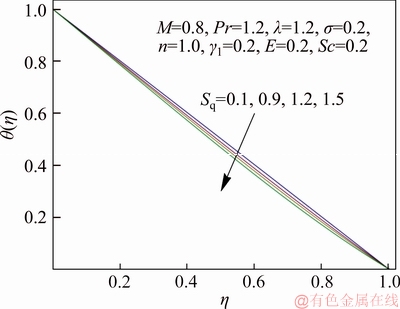
Figure 7 Variation of Sq on θ(η)
4.1 Flow characteristics
Figures 3 and 4 exhibit the vertical and horizontal distributions of flow velocity for variation in squeezing parameter Sq. The variation of the velocity components with Sq corresponds to squeezing flow generated by moving upper plate closer to lower plate creating pressure which results in an increment in fluid flow. In Figure 5, the horizontal component of velocity is graphed against η for some specific values of magnetic parameter (M). It is noticed that an increment in M corresponds to strong Lorentz force (resistive forces) which is responsible for decrement in fluid velocity above the centerline η=0.5. However, velocity follows an increasing trend with dominant M in the region below η=0.5. Figure 6 plots the drag force (or skin friction co-efficient) versus squeezing parameter Sq for several values of magnetic parameter M. The magnitude of skin friction co-efficient significantly decays as a result of increase in both Sq and M.
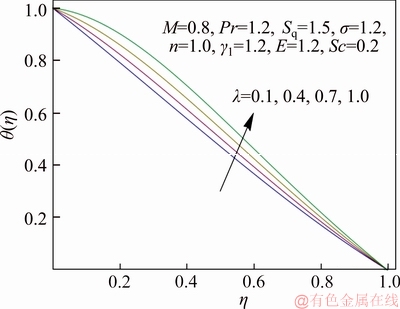
Figure 8 Variation of λ on θ(η)
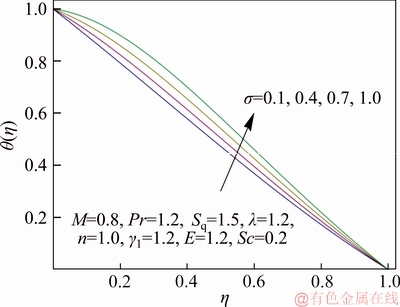
Figure 9 Variation of σ on θ(η)
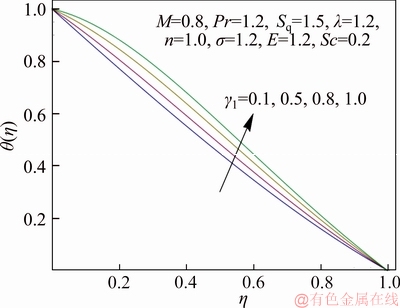
Figure 10 Variation of γ1 on θ(η)
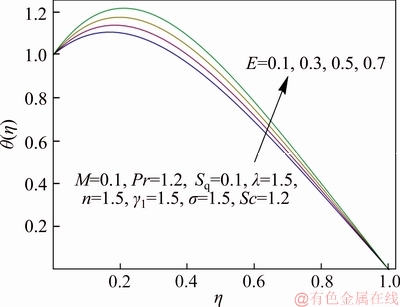
Figure 11 Variation of E on θ(η)
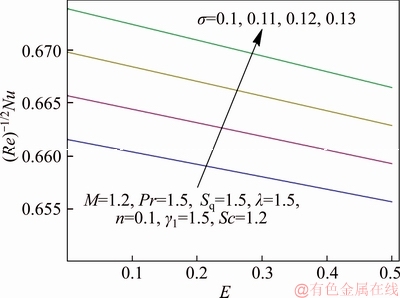
Figure 12 Variation of σ and E on Nu
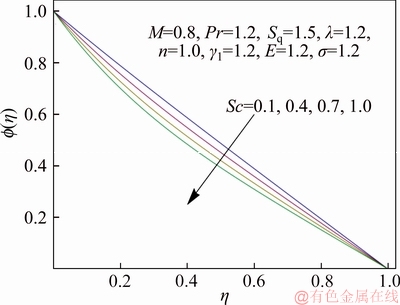
Figure 13 Variation of Sc on f(η)
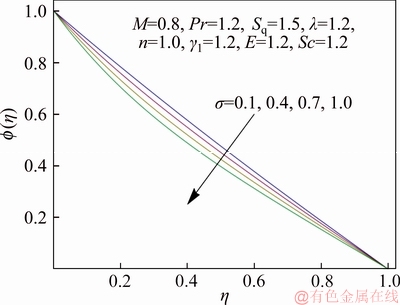
Figure 14 Variation of σ on f(η)
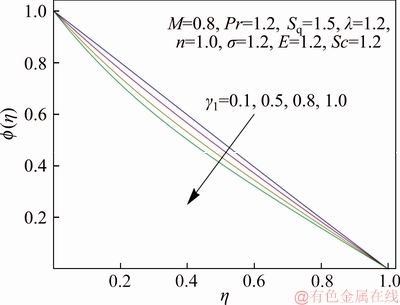
Figure 15 Variation of γ1 on f(η)
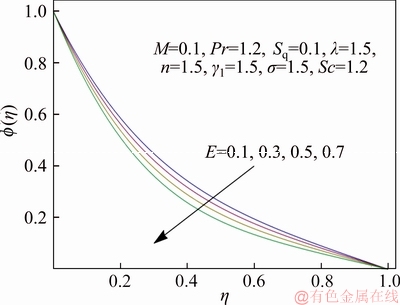
Figure 16 Variation of E on f(η)
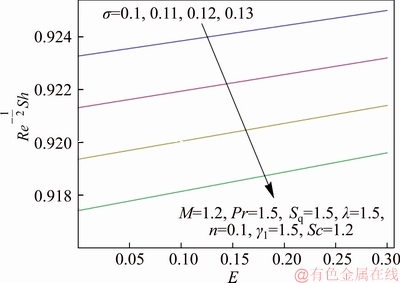
Figure 17 Variation of σ and E on Sh
4.2 Heat transfer characteristics
Figure 7 describes the impact of squeezing parameter Sq on temperature distribution. As expected, an enlargement in Sq counteracts the effects of momentum transfer rate and makes the temperature field decline. Figure 8 explains the effect of non-dimensional exothermic/endothermic parameter λ on temperature profile. It exposes that fluid temperature rises with elevation in λ. Physically larger value of λ gives more heat transfer to working fluid due to exothermic reaction which results in enhancement in temperature distribution. The variation of dimensionless reaction rate σ on temperature distribution is portrayed in Figure 9. For exothermic reaction, an increment in σ strengthens the temperature but reverse trend is accounted for endothermic reaction. Physically upgraded temperature elevates the reaction rate due to which the kinetic energy of reactant dominates allowing more collision between molecules consequently number of molecules increases. Figure 10 exhibits the temperature distribution for extensive range of temperature difference parameter γ1. Gradually rise in γ1 leads to cooling of upper plate so that lower plate becomes heated which results in increment in temperature field. Figure 11 demonstrates the variation in temperature field with deviation in non-dimensional activation energy parameter E. It indicates that temperature of fluid is an increasing function of E. As E enlarges, the number of very energetic particles with energies is equal to (or greater than) the activation energy increase which causes increase in fluid temperature and this happened in endothermic reaction. Features of dimensionless reaction rate σ and non- dimensional activation energy parameter E on Nusselt number are scrutinized in Figure 12. It is noticed that larger σ tends to enhance the Nusselt number whereas the effect of E on Nusselt number is qualitatively opposite to that of σ.
4.3 Mass transfer characteristics
Figure 13 discusses the variation of concentration field versus Schmidt number Sc. It highlights that enlarged Sc indicates smaller diffusion rate and hence concentration distribution decays. Figure 14 illustrates the curves of concentration field for varying dimensionless reaction rate σ. The fluid concentration reduces when σ is incremented. It means that chemical reaction strengthens the rate of interfacial mass transfer which decreases local concentration. Thus an increasing trend in concentration gradient and its flux leads to decrease in chemical specie’s concentration with an incremented chemical reaction rate. The variation of temperature difference parameter γ1 on concentration field is captured in Figure 15. Concentration decays for dominant γ1. Since solute concentration is decreasing function of γ1 and thus concentration increases when difference between lower and upper wall temperature enlarges. The behavior of dimensionless activation energy parameter E on concentration distribution is disclosed in Figure 16. It is noted that enlarging E causes decrement in concentration profile as high activation energy and resultant temperature leads to larger reaction rate constant which gives destructive chemical reaction and consequently the concentration profile decays. Figure 17 elucidates the influence of σ on Sherwood number versus E. It is seen that magnitude of Sherwood number has inverse relationship with dimensionless reaction rate σ while it is directly proportional to non-dimensional activation energy parameter E.
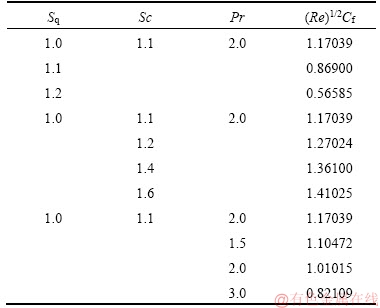
The outcomes for the drag force or skin friction co-efficient Cf are acquired for some values of squeezing parameter Sq, Schmidt number Sc and Prandtl number Pr with M=0. The comparison of the values of drag force Cf with published work [22] for a viscous fluid is listed in Table 2. The comparison illustrates an excellent agreement of our results with that of the past study [22].
Table 2 Comparison of skin friction co-efficient (Cf) for different values of Sq, Sc and Pr when M=0, λ=0, σ=0, η=0, γ1=0, E=0
5 Conclusions
The simultaneous impacts of binary chemical reaction and activation energy on hydro-magnetic squeeze flow mechanism are addressed.
1) The presence of magnetic effects decays the velocity distribution in the region η<0.5 but it strengthens the velocity field for η>0.5.
2) Non-dimensional exothermic/endothermic parameter λ increases the fluid temperature.
3) An increment in the value of temperature difference parameter γ1, dimensionless reaction rate σ and non-dimensional activation energy parameter E results in an increment in the value of temperature field.
4) The increment in the value of parameters σ, γ1 and E leads to delay of concentration field.
5) It is expected that the current communication is relevant to the physical modeling of utilitarian stretching flows especially in lubrication mechanism, magnetic polymer processing, designing of cooling/heating systems, energy estimation process, food processing and biomedical processes. Future investigations will prompt incentive more complicated fluid such as rate type fluid, nano-fluids with single phase model. Further, three-dimensional case can also be tackled.
Nomenclature
a
Dimensional constant
u, υ
Velocity components
p
Pressure
S
Extra stress tensor
J
Electric current density
T
Fluid temperature
B
Magnetic field
C
Fluid concentration
Th
Upper plate temperature
Uw
Stretching velocity
Tw
Lower plate temperature
Cw
Lower plate concentration
Ch
Upper plate concentration
k
Thermal conductivity
Sq
Squeezing parameter
Re
Reynolds number
Sc
Schmidt number
M
Magnetic parameter
Cf
Skin friction coefficient
Nu
Nusselt number
Sh
Sherwood number
Pr
Prandtl number
D
Diffusion co-efficient
cp
Specific heat capacity
kr
Chemical reaction rate constant
Ea
Activation energy
k*
Boltzmann constant
B0
Applied magnetic field
E
Dimensionless activation energy
parameter
v
Kinematics viscosity
γ
Dimensional constant
ρ
Fluid density
η
Similarity variable
Ψ
Stream function
θ
Dimensionless temperature
f
Dimensionless concentration
τxy
Shear stresses
μ
Dynamics viscosity
λ
Dimensionless exothermic/endothermic
Parameter
σ
Dimensionless reaction rate
γ1
Temperature difference parameter
σ*
Electric conductivity
β
Exothermic/endothermic co-efficient
References
[1] TENCER M, MOSS J S, ZAPACH T. Arrhenius average temperature: the effective temperature for non-fatigue wearout and long term reliability in variable thermal conditions and climates [J]. IEEE Transactions on Components and Packaging Technologies, 2004, 27(3): 602–607.
[2] MALEQUE K H A. Effects of exothermic/endothermic chemical reactions with Arrhenius activation energy on MHD free convection and mass transfer flow in presence of thermal radiation [J]. Journal of Thermodynamics, 2013: Article ID 692516.
[3] AWAD F G, MOTSA S, KHUMALO M. Heat and mass transfer in unsteady rotating fluid flow with binary chemical reaction and activation energy [J]. Plos One, 2014, 9: e107622 /1–12.
[4] SHAFIQUE Z, MUSTAFA M, MUSHTAQ A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy [J]. Results in Physics, 2016, 6: 627–633.
[5] ABBAS Z, SHEIKH M, MOTSA S S. Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation [J]. Energy, 2016, 95: 12–20.
[6] MUSTAFA M, MUSHTAQ A, HAYAT T, ALSAEDI A. Numerical study of MHD viscoelastic fluid flow with binary chemical reaction and Arrhenius activation energy [J]. International Journal of Chemical Reactor Engineering, 2017, 15. DOI: 10.1515/ijcre-2016-0131.
[7] MUSTAFA M, KHAN J A, HAYAT T, ALSAEDI A. Buoyancy effects on the MHD nanofluid flow past a vertical surface with chemical reaction and activation energy [J]. International Journal of Heat and Mass Transfer, 2017, 108: 1340–1346.
[8] ZAIB A, RASHIDI M M, CHAMKHA A J, MOHAMMAD N F. Impact of nonlinear radiation on stagnation-point flow of a Carreau nanofluid past a nonlinear stretching sheet with binary chemical reaction and activation energy [J]. Journal of Mechanical Engineering Science, 2017, 232(6): 962–972. DOI: 10.1177/0954406217695847.
[9] GIREESHA B J, KUMAR K G, RAMESH G K, PRASANNAKUMARA B C. Nonlinear convective heat and mass transfer of Oldroyd-B nanofluid over a stretching sheet in the presence of uniform heat source/sink [J]. Results in Physics, 2018, 9: 1555–1563.
[10] RAMESH G K, GIREESHA B J, SHEHZAD S A, ABBASI F M. Analysis of heat transfer phenomenon in magnetohydrodynamic Casson fluid flow through Cattaneo– Christov heat diffusion theory [J]. Communications in Theoretical Physics, 2017, 68(1): 91–95.
[11] KUMAR K G, RAMESH G K, GIREESHA B J, GORLA R S R. Characteristics of Joule heating and viscous dissipation on three-dimensional flow of Oldroyd B nanofluid with thermal radiation [J]. Alexandria Engineering Journal, 2017, 57(3): 2139–2149. DOI: org/10.1016/j.aej.2017.06. 006.
[12] RAMESH G K, PRASANNAKUMARA B C, GIREESHA B J, SHEHZAD S A, ABBASI F M. Three-dimensional flow of Maxwell fluid with suspended nanoparticles past a bidirectional porous stretching surface with thermal radiation [J]. Thermal Science and Engineering Progress, 2017, 1: 6–14.
[13] RAMESH G K, GIREESHA B J, HAYAT T, ALSAEDI A. Stagnation point flow of Maxwell fluid towards a permeable surface in the presence of nanoparticles [J]. Alexandria Engineering Journal, 2016, 55(2): 857–865.
[14] STEFAN M J. Attempts at apparent adhesion [J]. Annals of Physics, 1875, 230(2): 316–318.
[15] HAYAT T, MUHAMMAD T, QAYYUM A, ALSAEDI A, MUSTAFA M. On squeezing flow of nanofluid in the presence of magnetic field effects [J]. Journal of Molecular Liquids, 2016, 213: 179–185.
[16] ZHAO Q, XU H, TAO L. Unsteady bio-convection squeezing flow in horizontal channel with chemical reaction and magnetic field effects [J]. Mathematical Problem in Engineering, 2017, e2541413. DOI: 10.1155/2017/2541413.
[17] VAJRAVELU K, PRASAD K V, NG C, VAIDYA H. MHD squeeze flow and heat transfer of a nanofluid between parallel disks with variable fluid properties and transpiration [J]. International Journal of Mechanical and Materials Engineering, 2017, 12(9): 1–14.
[18] ULLAH I, RAHIM M T, KHAN H, QAYYUM M. Analytical analysis of squeezed flow in porous medium with MHD effect [J]. UPB Scientific Bulletin, Series A: Applied Mathematics Physics, 2016, 78(2): 281–292.
[19] SALAHUDDIN T, MALIK M Y, HUSSAIN A, BILAL S, AWAIS M, KHAN I. MHD squeezed flow of Carreau-Yasuda fluid over sensor surface [J]. Alexandria Engineering Journal, 2017, 56: 27–34.
[20] GORJI M R, POURMEHRAN O, BANDPY M G, GANJI D D. Unsteady squeezing nanofluid simulation and investigation of its effect on important heat transfer parameters in presence of magnetic field [J]. Journal of Taiwan Institute of Chemical Engineering, 2016, 67: 467–475.
[21] QAYYUM M, KHAN H, KHAN O. Slip analysis at fluid solid interface in MHD squeezing flow of Casson fluid through porous medium [J]. Results in Physics, 2017, 7: 732–750.
[22] MUHAMMAD N, NADEEM S, MUSTAFA T. Squeezed flow of a nanofluid with Cattaneo–Christov heat and mass fluxes [J]. Results in Physics, 2017, 7: 862–869.
[23] SHAMSHUDDIN M D, B G O A, RAM M S, KADIR A. Finite element computation of multi-physical micropolar transport phenomena from an inclined moving plate in porous media [J]. Indian Journal of Physics, 2018, 92: 215–230.
G O A, RAM M S, KADIR A. Finite element computation of multi-physical micropolar transport phenomena from an inclined moving plate in porous media [J]. Indian Journal of Physics, 2018, 92: 215–230.
[24] SHAMSHUDDIN M D, MISHRA S R, B G O A, KADIR A. Unsteady reactive magnetic radiative micropolar flow, heat and mass transfer from an inclined plate with joule heating: A model for magnetic polymer processing [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 233(4): 1246–1261. DOI: 10.1177/0954406218768837.
G O A, KADIR A. Unsteady reactive magnetic radiative micropolar flow, heat and mass transfer from an inclined plate with joule heating: A model for magnetic polymer processing [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 233(4): 1246–1261. DOI: 10.1177/0954406218768837.
[25] THUMMA T, SHAMSHUDDIN M D. Buoyancy ratio and heat source effects on MHD flow over an inclined non-linearly stretching sheet [J]. Frontiers in Heat and Mass Transfer, 2018, 10: 1–12.
[26] SHAMSHUDDIN M D, B G O A, REDDY S S, KADIR A. Rotating unsteady multi-physico-chemical magneto- micropolar transport in porous media: Galerkin finite element study [J]. Computational Thermal Sciences: An International Journal, 2018, 10: 167–197.
G O A, REDDY S S, KADIR A. Rotating unsteady multi-physico-chemical magneto- micropolar transport in porous media: Galerkin finite element study [J]. Computational Thermal Sciences: An International Journal, 2018, 10: 167–197.
[27] B G O A, ESPINOZA D E S, KADIR A, SHAMSHUDDIN M D, SOHAIL A. Experimental study of improved rheology and lubricity of drilling fluids enhanced with nano-particles [J]. Applied Nanoscience, 2018, 8(5): 1069–1090.
G O A, ESPINOZA D E S, KADIR A, SHAMSHUDDIN M D, SOHAIL A. Experimental study of improved rheology and lubricity of drilling fluids enhanced with nano-particles [J]. Applied Nanoscience, 2018, 8(5): 1069–1090.
[28] LIAO S J. Beyond perturbation: Introduction to Homotopy analysis method [M]. Boca Raton: Chapman and Hall, CRC Press, 2003.
[29] LIAO S J. Homotopy analysis method in non-linear differential equations [M]. Heidelberg: Springer and Higher Education Press, 2012.
[30] HAYAT T, ALI S, AWAIS M, OBAIDAT S. Stagnation point flow of Burgers’ fluid over a stretching surface [J]. Progress in Computational Fluid dynamics: An International Journal, 2013, 13(1): 48–53. DOI: 10.1504/PCFD.2013.050650.
[31] HAYAT T, ALI S, AWAIS M, ALHUTHALI M S. Newtonian heating in stagnation point flow of Burgers fluid [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36: 61–68.
[32] FAROOQ M, KHAN M I, WAQAS M, HAYAT T, ALSAEDI A, KHAN M I. MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects [J]. Journal of Molecular Liquids, 2016, 221: 1097–1103.
[33] WAQAS M, HAYAT T, SHEHZAD S A, ALSAEDI A. Transport of magnetohydrodynamic nanomaterial in a stratified medium considering gyrotactic microorganisms [J]. Physica B: Condensed Matter, 2018, 529: 33–40.
[34] HAYAT T, JABEEN S, SHAFIQ A, ALSAEDI A. Radiative squeezing flow of second grade fluid with convective boundary conditions [J]. Plos One, 2016, 11(4): e0152555.
[35] MABOOD F, KHAN W A, ISMAIL A I M. MHD flow over exponential radiating stretching sheet using homotopy analysis method [J]. Journal of King Saud University- Engineering Sciences, 2017, 29: 68–74.
[36] FAROOQ M, QURAT U L, AIN ANZAR, HAYAT T, KHAN M I, ANJUM A. Local similar solution of MHD stagnation point flow in Carreau fluid over a non-linear stretched surface with double stratified medium [J]. Results in physics, 2017, 7: 3078–3089.
[37] HAYAT T, AHMAD S, KHAN M I, ALSAEDI A. Modeling and analyzing flow of third grade nanofluid due to rotating stretchable disk with chemical reaction and heat source [J]. Physica B: Condensed Matter, 2018, 537: 116–126.
(Edited by FANG Jing-hua)
中文导读
具有二元化学反应和活化能的压缩流体的磁流体动力学
摘要:研究了在外加磁场作用下,黏性流体在压缩通道中的运动规律。热量和质量传输过程涉及温度依赖的二元化学反应和修正的Arrhenius活化能函数理论,但是该理论尚未揭示挤压流动机理。在无滑移壁边界条件下,流场、热场和质量场通过无量纲、高度非线性的常微分方程来控制。采用一种收敛性稳定的解析方法求解边值问题。对各种新出现参数的流速场、温度场和流体浓度分布的图进行了详细的研究,获得了表面摩擦、Nusselt和Sherwood数并以图表形式表现。结果表明,流体温度随着占主导地位的无量纲反应速率σ和活化能E的增加而升高。然而,σ和E的增加随着流体浓度的增加而下降。当前研究应用于许多工程和工业过程包括聚合物工业、压缩和注塑成型、润滑系统、纸张的生产、塑料薄膜的成型。在化学工程和地热领域,可以利用磁场来控制核冷却反应、核或化学系统、双分子反应、生化过程和导电聚合物流动。在这些应用的推动下,此研究已得到发展。
关键词:挤压流;磁流体动力学;活化能;二元化学反应
Received date: 2018-05-14; Accepted date: 2018-07-04
Corresponding author: S. AHMAD, PhD; Tel: +923335377399; E-mail: shakeel_oiiui@hotmail.com; ORCID: 0000-0003-2734-3890