复杂矿床三维可视化建模关键技术

荆永滨¹，刘晓明²，毕林²

(1. 河南工程学院 安全工程学院，河南 郑州，451191；

2. 中南大学 资源与安全工程学院，湖南 长沙，410083)

摘要：为实现复杂矿床空间形态和矿石品位分布的三维表达，构建真实的矿床三维地质环境，研究复杂矿床建模与可视化系统构建的关键技术。采用一些复杂的算法将矿体表面模型和块段模型结合成一种混合模型方案，包括从原始地勘数据建立钻孔三维模型；轮廓线贴面重构矿床三维表面模型；通过表面模型构建八叉树结构存储的块段模型，构建块段模型时采用方向包围盒(OBB)进行相交检测，用Feito–Torres方法进行包含检测；应用地质统计学方法对块段模型单元块的矿石品位进行估值。通过这些技术能够快速准确地建立复杂矿床表面模型和块段模型，构建三维可视化的采矿地质环境，为矿山提供直观、逼真的开放式基础数据源。

关键词：复杂矿床模型；三维可视化；块段模型；品位估值

中图分类号：TD672；TP391.72            文献标志码：A         文章编号：1672-7207(2014)09-3104-07

Key techniques for 3D visual modeling of complex mineral deposits

JING Yongbin¹, LIU Xiaoming², BI Lin²

(1. School of Safety Engineering, Henan Engineering Institute, Zhengzhou 451191, China;

2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: To present the spatial shape and grade distribution of complex mineral deposit in 3D space and to establish the real 3D geological environment of complex mineral deposit, the key techniques for building complex deposit modeling and visualization system were discussed. A number of sophisticated algorithms were implemented to integrate the deposit surface model and block model to a new scheme of hybrid model. 3D borehole model was created by multi-source exploration data. A surface model of deposit was reconstructed through tiling method from planar contour lines. Robust conversion method of block model from complex deposit model was proposed. An octree with force subdivision was used as data structure of block model with subdivision blocks on the boundary. OBB collision detection and Feito-Torres algorithm were employed for the intersect test and inclusion test between a block and surface model. Ore grades of cells within block model were estimated by geostatistical techniques. Through the above techniques, the 3D geological environment of complex surface model and block model of complex deposit can be built rapidly and accurately. So as a visual and realistic open data source of mineral deposit for various mining activities is provided.

Key words: complex deposit modeling; three-dimensional visualization; block model; grade estimation

地质形态是空间三维的，在20世纪90年代三维软件开发之前，处理全维地质数据几乎是不可能的。随着三维图形技术的发展，强大的三维图形功能可以为软件使用者提供直观、逼真的三维可视化效果以及便捷的人机交互。近年来，三维地质建模软件(Gocad, Lynx, Earth Vision等)的发展为地球科学开辟了一个新领域。如今，数据库、GIS和三维可视化软件已经成为地质学家成图、分析、综合、建模和解释地质数据的常用工具^[1]。在矿业工程领域，矿床的三维空间几何形态、元素品位属性空间分布情况和矿产资源储量是矿山投资决策、开采设计、方案优化、品位控制和生产计划编制等的先决条件^[2-3]。传统二维图纸仍然是基础的表示方法，但因其缺少一维的数据，导致对空间关系容易产生曲解。要使其更容易被理解，就应该使用高性能三维可视化技术展示矿床的空间形态和品位属性，而不只是一些符号和颜色。实际矿山中大多数矿床赋存条件较为复杂，一方面矿体空间形态上存在分支复合等变化，通过相距甚远的相邻剖面建立矿体三维模型的算法不够完善，目前都是完全借助地质工程师的经验进行人工交互式建模。另一方面矿石品位在空间不同位置的数值存在较大差异，现有的品位估值块段模型建模方法不能够较为准确的模拟复杂矿体形态。因此，基于三维图形技术的复杂矿床可视化建模及品位估值系统的研究与开发对于理论研究和实际应用都有重要的意义。

1  系统核心模块

矿床建模和品位估值基于原始的地质勘探工程和生产勘探工程数据，数据内容包括工程空间位置和矿石品位、岩性、体重等属性信息。在三维空间形成工程轨迹，在各个勘探线剖面上进行矿体边界圈定和断层线确定。对于大部分生产矿山，已有的经过地质解译产生的各种平剖面图则可以直接利用，矿床三维可视化建模过程如图1所示。

本文针对诸多矿山实际数据，对复杂矿床可视化建模和品位估值中的核心技术模块予以实现。包括钻孔三维模型、基于轮廓线的矿床表面模型建模、块段模型建模和块段品位估值算法等。

2  地质数据管理与可视化技术

勘探数据是矿床三维可视化建模的数据基础，对勘探数据的管理方式以及数据的三维可视化研究将直接关系到三维地质建模的准确性和便捷性。

2.1  勘探数据的存储与管理

勘探数据来源多样，且复杂多变，但这些数据中最主要且最具有代表性的一种数据是钻孔工程数据。而其他类型的勘探数据经过相应的计算和转换后均可以抽象为钻孔数据。钻孔工程的特点是沿其迹线方向上分布有许多取样段起始点、岩层分界点等控制性点。为了满足存储、查询与修改钻孔数据及制图、三维数据显示的需要，将钻孔工程数据综合成一个数据库，分为4个表进行存储，分别是孔口数据表、测斜数据表、样品分析数据表和岩性数据表。

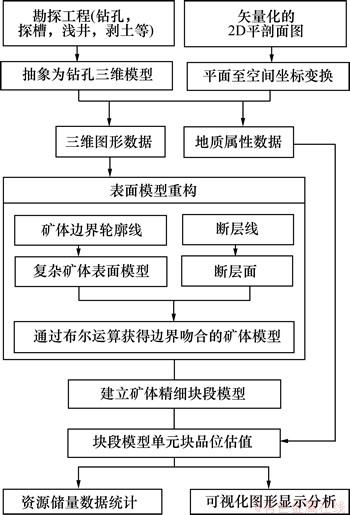
图1  复杂矿床三维可视化建模流程

Fig. 1  Workflow for 3D visual modeling of complex mineral deposits

2.2  钻孔三维模型

钻孔在钻进过程中受诸多因素影响，钻进轨迹实际是一条变化连续的复杂空间曲线。在应用过程中，通常按照一定的深度间距测量不同深度处的方位角和倾角，然后根据各种钻孔轨迹数学模型计算连续的空间折线来近似的逼近钻孔轨迹曲线。主要的钻孔轨迹数学模型有均角全距法、全角半距法和最小曲率法等^[4-5]。计算时，钻孔地理坐标中的东坐标、北坐标和高程分别对应笛卡尔坐标系中的x，y和z，孔口坐标x₀，y₀和z₀为已知值，则可以逐段计算测点的空间坐标。

钻孔三维模型可视化是指在三维环境下表现钻孔数据，除包括钻孔轨迹所包含的几何数据以外，还要有钻孔名、样品段的起始点深度、品位值以及岩性等属性数据。因此，采用几何图形和数据表混合的数据结构存储钻孔三维可视化结果。每个几何图形的属性对应数据表中的一条记录，当需要显示图形的某种属性时，只需从表中取出其相应的记录值即可。

属性数据的可视化，可以通过颜色、图形、符号等实现。例如将元素的品位值按数值区间以不同的颜色显示样品段；或将品位值以直方图或曲线的方式显示在钻孔一侧；或将岩性按照不同的岩性代码以不同的纹理显示在钻孔一侧；另外，任何属性数据均可以用文字的形式显示在几何图形附近。图2所示为某矿山钻孔三维模型。

图2  钻孔三维模型

Fig. 2  3D model of boreholes

3  基于轮廓线的复杂表面模型建模

经过地质解译得到的矿体边界、断层、岩层等信息均存储为二维轮廓线，利用这些轮廓线重构复杂表面是三维模型建模中的关键步骤。基于轮廓线的表面模型建模包括3个关键问题，轮廓线对应、轮廓线贴面和分支处理^[6]。图3所示为基于矿体轮廓线的复杂表面模型建模。这3个问题都存在弱约束的特点，具有很大的随意性。其中，前者属于拓扑重建，后两者属于几何重建。

3.1  轮廓线贴面优化算法

贴面是三维模型重构的核心，其最终目标是在2条轮廓线间生成三角网。由于三角形网格表示的模型简单灵活、边界适应性好，在真实感图形显示等方面具有明显优势。2条轮廓线间贴面的过程可以表示为图论中有向环路图的搜索过程^[6-7]，如图4所示。

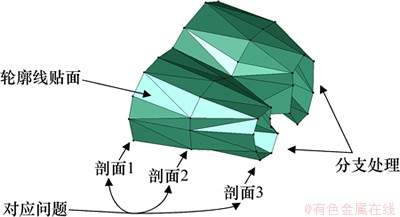
图3  基于矿体轮廓线的复杂表面模型建模

Fig. 3  Surface modeling from contour lines of complex orebody

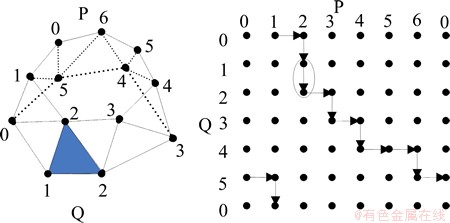
图4  表示三角网的有向环路图

Fig. 4  Oriented cycle of tiling to represent triangle mesh

其中，轮廓线用一系列有顺序的点数据来表示，连接相同轮廓线上相邻两点的边称之为轮廓线段，连接不同轮廓线上两点的边称之为跨距。轮廓线段与对应轮廓线上的1点与该线段形成的2个跨距构成一个基本三角面片，如图4中填充三角形。用上面轮廓线的顶点定义一个二维图形的行，下面轮廓线的顶点定义图形的列。二维图形中每条边确定2条轮廓线之间的一个三角形，三角形的顶点由图形中唯一的行和列数确定。例如，右图中圈出的边表示左图中的填充三角形。环路图中边的权重定义为其代表的三角形的一种度量值，例如面积、边长等，通过搜索环路中最小或最大权重路径的方法来生成优化的表面模型三角网。

3.2  复杂分支处理

如果相邻2个剖面上分别有m和n条轮廓线时，就会存在分支问题，其中m≠n，且m，n＞0。对于分支问题的解决，通常是对存在分支问题的相邻剖面上的轮廓线进行处理，形成多条过渡轮廓线。

在矿床三维可视化建模系统中，依据已有方法的优点以及矿体三维建模的特点，对于分支问题的处理，由用户将未分支轮廓线划分为对应分支轮廓线个数的多个区域，形成多个一一对应的轮廓线，然后分别进行轮廓线贴面。但用户根据经验构造过渡轮廓线存在很大的随意性，有时需进行多次操作才能建立较好的矿体表面模型。因此，本文采用线性插值中轴线的方法构造过渡轮廓线，从而建立存在复杂分支的矿体模型，其流程如图5所示。

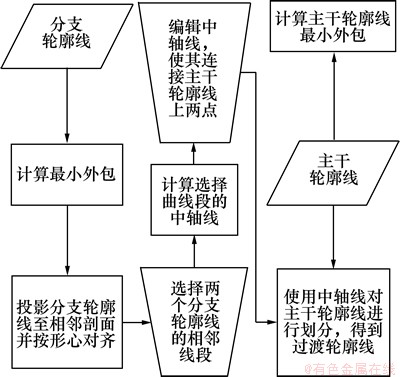
图5  中轴线法构造分支的过渡轮廓线

Fig. 5  Intermediate contour lines of branches built by medial axis

4  精细块段模型建模

块段模型属于体模型，用于表示矿床属性的内部变化特征，用于模拟非均匀矿体的空间分布。块段模型是矿床品位推估及储量计算、露天矿境界优化、生产计划编制和有限元模拟等的基础。块段模型建模的基本思想是将矿床表面模型所包含的三维空间区域按照一定的尺寸划分为众多的单元块，边界处的单元块进行细分。这种边界单元块细分的精细块段模型能够更加准确的模拟矿体形态。然后对块段模型的单元块的品位属性根据已知的样品进行估算，并在此基础上进行储量的计算^[8-10]。

4.1  块段模型数据结构

传统的块段模型包括规则栅格模型和边界细分模型2种。规则栅格模型内所有单元块具有同样的尺寸，但若要准确模拟矿体的形态则需将单元块尺寸减小，因此极大的增加了单元块数量。边界细分模型只将处于模型边界的单元块次分为更小的单元块，这些单元块存储为固定结构的数组，每个记录存储单元块中心点坐标及单元块属性，这种块段模型数据结构存储量大，检索速度慢^[8]。

因此，本文选择八叉树作为块段模型的数据结构。八叉树是将四叉树推广到三维而形成的一种空间数据结构，具有广泛的应用。八叉树数据结构能够以不同层次的单元块索引空间属性数据，可以使块段模型在保持减小额外计算量的前提下加快检索速度^{[9, 11]}。此外，不同的单元块尺寸能够较准确地模拟矿体形态和边界特征。八叉树的层次结构、递归细分等特点还能够提高块段模型建模的运算速度。

4.2  块段模型算法实现

一般情况，块段模型的单元块由基本单元块和细分单元块组成，所有基本单元块尺寸都相同，细分单元块的尺寸根据细分级别相应缩小。因此在构建八叉树时，需要对模型内部的节点强行细分，直到达到基本单元块尺寸的要求。八叉树块段模型的算法流程如图6所示。

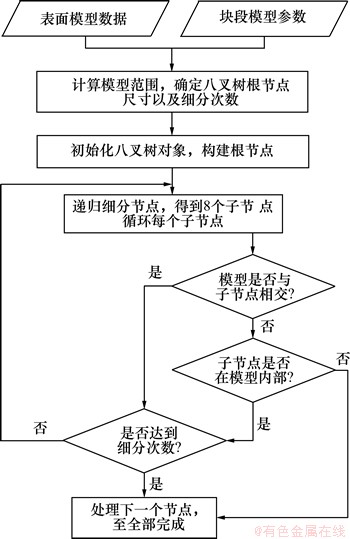
图6  八叉树块段模型的算法流程

Fig. 6  Algorithm for building octree block model

算法的核心是判断单元块与矿体表面模型的关系，即相交检测和包含检测。单元块与表面模型的相交检测过程借助于方向包围盒层次树(OBB)实现^[12]。利用方向包围盒层次树这种空间索引机制，可以很大程度上减少表面模型三角形面片之间的相交测试次数。

单元块与表面模型的相交检测过程如下，首先建立表面模型的方向包围盒层次树，将单元块构建为一个OBB节点，然后从表面模型OBB树的根节点开始与单元块OBB节点进行相交检测。如果二者相交，则判断该节点是否为叶节点，若不是叶节点，则继续与其子结点进行相交检测；若是叶节点，则取出该节点中的三角面分别与单元块OBB节点进行相交检测，如果有相交就确定块段模型单元块与表面模型相交。

经过单元块与矿体表面模型的相交检测后，要判断不相交的单元块是否在矿体表面模型内部。单元块在多面体内外判断简化为单元块中心点在多面体内外的判断。点在多面体内外的判断是整个建模过程中最重要的算法，直接影响到块段模型的准确性和建模时间。点在多面体内的判断通常使用射线法和BSP法，但两者对于处理复杂多面体存在缺点^[13]。因此，本文采用一种快速检测包含关系的健壮算法，Feito–Torres法^[10]。该方法不考虑多面体的形状因素且对多面体容错性强，只跟多面体的面个数成线性关系。

用Feito–Torres法判断点在多面体内外，既不要解方程也不需要计算三角函数，而且实现简单。文献[13-14]中介绍了该算法的理论基础。基本思想是将多面体分解为由三角形顶点和坐标原点构成的四面体集，检测得到包含该点的四面体子集，然后计算子集内四面体的符号体积和，四面体符号体积为正则+1，为负则-1，为零则+0。最后根据计算结果确定点在多面体的内外。如果结果＞0，点在多面体内；如果结果≤0，则点在多面体外。四面体的符号体积使用行列式进行计算，算法实现非常简单。

5  块段模型属性估值

块段模型将矿体表面模型内部空间划分为一组大小不等的单元块，此时单元块只具有所属表面模型的区域属性。单元体块其他地质属性都需根据原始地质数据通过空间插值方法得到。矿石品位是诸多属性中最主要的属性之一。目前有许多方法用于矿石品位估值，其中地质统计学方法在估值精度上明显优于其他方法，而且能够提供估计方差。因此，地质统计学方法得到广泛的应用，已成为储量估算的标准之一。地质统计学是以区域化变量理论为基础，以变异函数为工具，研究空间数据的随机性和结构性的数学地质方法^[15-16]。块段模型的地质统计学方法品位估值过程主要分为区域化变量结构分析、空间数据搜索和求解克里格方程，其流程如图7所示。

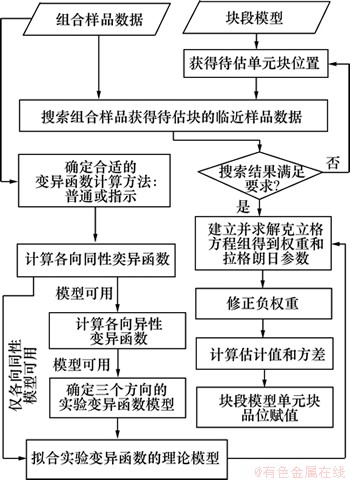
图7  块段模型地质统计方法品位估值流程

Fig. 7  Workflow for grade estimation of block model using geostatistic method

6  工程实例

实例中铜矿位于云南省，该铜矿床是一个地质构造十分复杂的矿体，矿体从下至上分为I1，I2和I3共3个层状铜矿体，断层总计有48条，矿体被矿区内错综复杂的断层将其切割成许多小矿体，将这些断层信息真实的反映在矿床模型上是非常必要的。使用复杂矿床建模技术对该矿床进行三维可视化建模，建立好的断层模型和经断层切割后的矿体表面模型见图8和9。

块段模型的尺寸参数为：基本单元块尺寸8 m×8 m×2 m；边界单元块细分2次，尺寸为2 m×2 m×0.5 m。矿体铜品位估值结果的三维空间分布如图10所示，单元块的铜品位值按照区间用不同的颜色表示。图11所示为一小块矿体表面模型和块段模型的切片，可以看出块段模型对矿体表面模型的形状模拟非常吻合。

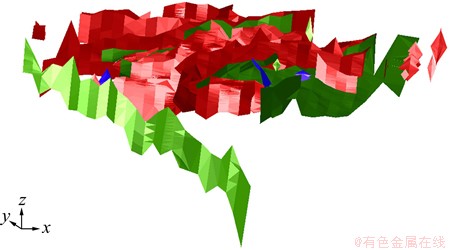
图8  矿区内的断层表面模型

Fig. 8  Surface models of faults at mining area

图9  铜矿体模型

Fig. 9  3D model of copper deposit

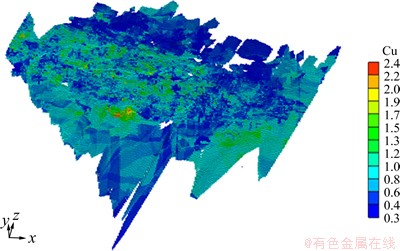
图10  矿体铜品位块段模型估值结果

Fig. 10  Block model of orebody with estimated copper grade value

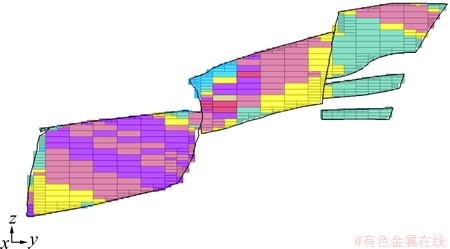
图11  切割后的表面模型和块段模型混合模型

Fig. 11  Slice of hybrid model composed of surface model and block model

7  结论

1) 研究矿床三维可视化建模的关键技术，通过这些技术将三维图像技术应用于矿产资源的展示、计算和分析中。

2) 提出基于数据库的几何图形加属性数据的钻孔三维模型创建方法。采用基于二维轮廓线贴面算法重构矿体三维表面模型，能够创建包括分支在内的各种复杂矿体模型。

3) 使用八叉树数据结构存储块段模型，从而加速单元块空间索引，减小数据量；提高了块段模型建模速度和健壮性，且更加准确的模拟复杂的矿体形态。采用地质统计学方法分析矿石品位空间变异性，并对块段模型单元块进行品位估值。

4) 采用矿体表面模型加块段模型的混合模型能够很好的研究矿体形态和品位的空间分布情况，为矿山开采可行性研究、地下矿开采设计、露天矿境界优化和矿山生产计划等提供数据基础。

参考文献:

[1] Zanchi A, Donatis M D, Gibbs A, et al. Imaging geology in 3D[J]. Computers & Geosciences, 2009, 35(1): 1-3.

[2] 熊书敏, 王李管, 黄俊歆, 等. 地下矿可视化生产管控系统参数化数据模型[J]. 中南大学学报: 自然科学版, 2012, 43(1): 272-277.

XIONGShumin, WANGLiguan, HUANGJunxin, et al. Parametric data model for underground mine 3D visual production management and control system[J]. Journal of Central South University: Science and Technology, 2012, 43(1): 272-277.

[3] 周智勇, 陈建宏, 杨立兵. 大型矿山地矿工程三维可视化模型的构建[J]. 中南大学学报(自然科学版), 2008, 39(3): 423-428.

ZHOU Zhiyong, CHEN Jianhong, YANG Libing 3D visualization modeling on geological and mining engineering in a large-sized mine[J]. Journal of Central South University (Science and Technology), 2008, 39(3): 423-428.

[4] 冯治东, 周晓将, 卢才武, 等. 基于Hoops的钻孔三维可视化技术研究[J]. 地理与地理信息科学, 2011, 27(3): 38-41.

FENG Zhidong, ZHOU Xiaojiang, LU Caiwu, et al. Aresearch on 3D visualization of drillings based on hoops[J]. Geography and Geo-InformationScience, 2011, 27(3): 38-41.

[5] 李静, 张金昌, 陈晓琳. 地质勘探钻孔轨迹计算新模型[J]. 探矿工程: 岩土钻掘工程, 2011, 38(1): 22-24.

LI Jing, ZHANG Jinchang, CHEN Xiaoli. New model for drilling trajectory calculation in geo-exploration[J]. Exploration Engineering: Rock&SoilDrillingandTunneling, 2011, 38(1): 22-24.

[6] Meyers D, Skinner S, Sloan K. Surfaces from contours[J]. ACM Transactions on Graphics, 1992, 11(3): 228-258.

[7] Fuchs H, Kedem Z M, Uselton S P. Optimal surface reconstruction from planar contours[J]. Communications of the ACM, 1977, 20(10): 693-702.

[8] 王恩德, 孙立双, 毛亚纯, 等. 一种适于矿体储量计算的矢量栅格混合模型[J]. 中国矿业, 2007, 16(6): 72-74.

WANG Ende, SUN Lishung, MAO Yachun, et al. One kind of the vector grid hybrid model being suitable for orebody reserve calculation[J]. China Mining Magazine. 2007, 16(6): 72-74.

[9] 毕林, 王李管, 陈建宏, 等. 基于八叉树的复杂地质体块段模型建模技术[J]. 中国矿业大学学报, 2008, 37(4): 532-537.

BI Lin, WANG Liguan, CHEN Jianhong, et al. Study of octree-based block model of complex geological bodies[J]. Journal of China University of Mining and Technology, 2008, 37(4): 532-537.

[10] 荆永滨, 王李管, 毕林, 等. 复杂矿体的块段模型建模算法[J]. 华中科技大学学报(自然科学版), 2010, 38(2): 97-100.

JING Yongbin, WANG Liguan, BI Lin, et al. Robust creation of block model from complex orebody model[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2010, 38(2): 97-100.

[11] Melero F J, Cano P, Torres J C. Bounding-planes Octree: A new volume-based LOD scheme[J]. Computers & Graphics, 2008, 32(4): 385-392.

[12] Gottschalk S, Lin MC, Manocha D. OBBTree: A hierarchical structure for rapid interference detection[C]// Proceedings of the 23rd annual conference on Computer graphics and interactive techniques. New York, USA: ACM Press, 1996: 171-180.

[13] Ogayar C J, Segura R J, Feito F R. Point in solid strategies[J]. Computers & Graphics, 2005, 29(4): 616-624.

[14] Feito F R, Torres J C. Inclusion test for general polyhedra[J]. Computers & Graphics, 1997, 21(1): 23-30.

[15] 侯景儒, 黄竞先. 地质统计学在固体矿产资源/储量分类中的应用[J]. 地质与勘探, 2001, 37(6): 61-66.

HOU Jingru, HUANG Jingxian. Application of geostatistics in classification for resources/reserves of solid fuels and mineral commodities[J]. Geology and Prospecting, 2001, 37(6): 61-66.

[16] Ali Akbar D. Reserve estimation of central part of Choghart north anomaly iron ore deposit through ordinary kriging method[J]. International Journal of Mining Science and Technology, 2012, 22(4): 573-577.

(编辑  陈爱华)

收稿日期：2013-11-22；修回日期：2014-03-20

基金项目：河南省教育厅科学技术研究重点项目(13B440925)；中国博士后科学基金资助项目(2012M511417)

通信作者：荆永滨(1981-)，男，河南郑州人，讲师，博士，从事矿山三维模拟及科学计算可视化方面的研究；电话：15188387323；E-mail: jingyongbin@gmail.com