J. Cent. South Univ. Technol. (2008) 15: 575-580
DOI: 10.1007/s11771-008-0108-6
Hot deformation behaviors and flow stress model of GCr15 bearing steel
LIAO Shu-lun(廖舒纶)1, 2, ZHANG Li-wen(张立文)1, 2, YUE Chong-xiang(岳重祥)1, 2,
PEI Ji-bin(裴继斌)1, 2, GAO Hui-ju(高惠菊)3
(1. State Key Laboratory for Materials Modification, Dalian University of Technology,
Dalian 116023, China;
2. School of Materials Science and Engineering, Dalian University of Technology,
Dalian 116023, China;
3. Rod and Wire Continuous Rolling Mill, Dongbei Special Steel Group, Dalian 116031, China)
Abstract: The hot deformation behaviors of GCr15 bearing steel were investigated by isothermal compression tests, performed on a Gleeble-3800 thermal-mechanical simulator at temperatures between 950 ℃ and 1 150 ℃ and strain rates between 0.1 and 10 s-1. The peak stress and peak strain as functions of processing parameters were obtained. The dependence of peak stress on strain rate and temperature obeys a hyperbolic sine equation with a Zener-Hollomon parameter. By regression analysis, in the temperature range of 950-1 150 ℃ and strain rate range of 0.1-10 s-1, the mean activation energy and the stress exponent were determined to be 351kJ/mol and 4.728, respectively. Meanwhile, models of flow stress and dynamic recrystallization (DRX) grain size were also established. The model predictions show good agreement with experimental results.
Key words: GCr15 bearing steel; flow stress; dynamic recystallization; hot deformation
1 Introduction
Hot deformation with dynamic recrystallization (DRX) can cause significant microstructural changes and is recognized as an important method to control the final mechanical properties of materials. Hot deformation behaviors are generally reflected by flow curve which is a direct consequence of microstructural changes involving work hardening (WH), dynamic recovery(DRV) and dynamic recrystallization(DRX). The calculation of the forces required to deform the material is an important aspect of mechanical design of metal working processes. In order to employ advanced modeling technique, such as finite element analysis, the constitutive equation of flow stress must be determined. Since some early work on hot deformation behavior of plain-carbon steel has been reported, many researchers began to concentrate their attention on some other materials. For instance, there have been some studies on hot deformation behavior of copper[1] and some alloys[2-6]. EBRAHIMI et al[7] described the model of stress—strain curves of Ti-IF steel at high temperature. CABRERA et al[8] studied hot deformation behavior of duplex stainless steel. The recrystallization behavior of some steels was also investigated[9-14]. GCr15 steel is a high-carbon-chromium bearing steel widely used in industries. However, little attention has been paid to the study on the deformation characteristics and flow behavior at high temperature for GCr15 bearing steel[15-16]. The subject is of importance in manufacturing applications, such as hot rolling.
In this investigation, the charateristic parameters, such as the peak stress and the peak strain, were described. The constitutive equation of stress—strain curves was expressed in terms of dynamic recovery region and dynamic recrystallization region, in which the effect of dynamic recrystallization on flow softening was considered. The model of DRX grain size was also obtained. The study can provide useful models and experimental data for optimizing production process of GCr15 bearing steel.
2 Experimental procedure
The composition of the GCr15 steel employed in this research was 0.99C, 0.24Si, 0.31Mn, 0.01P, 0.003S, 1.44Cr, 0.05Ni, 0.12Cu, 0.02Mo, all numbers were given in mass fraction (%). The specimens were all machined from the hot-rolled bar and turned to 8 mm in diameter and 12 mm in height.
Compression tests were carried out at constant strain rates from 0.1 to 10 s-1 and at temperatures from 950 to 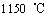 on the Gleeble-3800 simulator. all samples were first heated up to 1 150 ℃ at the heat rate of 5 ℃/s. After holding at 1 150 ℃ for 8 min to ensure that the specimens had a uniform temperature and a desired grain size, the specimens were cooled to different deformation temperatures. After being held for a while for uniformity in the tested temperature, the specimens were deformed to various strains (maximum of 1) at strain rates of 0.1-10 s-1. After hot deformation, the specimens were immediately quenched in water to capture the microstructure of hot deformed material. Optical micrographs were obtained from the cross-sectional surface of the deformed specimens that were cut parallel to the compression axis.
on the Gleeble-3800 simulator. all samples were first heated up to 1 150 ℃ at the heat rate of 5 ℃/s. After holding at 1 150 ℃ for 8 min to ensure that the specimens had a uniform temperature and a desired grain size, the specimens were cooled to different deformation temperatures. After being held for a while for uniformity in the tested temperature, the specimens were deformed to various strains (maximum of 1) at strain rates of 0.1-10 s-1. After hot deformation, the specimens were immediately quenched in water to capture the microstructure of hot deformed material. Optical micrographs were obtained from the cross-sectional surface of the deformed specimens that were cut parallel to the compression axis.
3 Results and discussion
3.1 Stress—strain curves and deformed microstruc- tures
Fig.1 shows the stress—strain curves of the GCr15 bearing steel. Referring to Fig.1, the flow stress in the strain rate range of 0.1-1 s-1 increases to a peak value which is followed by a strain softening and a steady state flow. These curves exhibit a typical behavior of DRX. As shown in Fig.1, the peak stress decreases with the increase of the temperature. Likewise, it decreases as the strain rate decreases. Under high strain rates of 5.0 and 10.0 s-1, when the strain surpasses a critical value, the flow curves show a flat shape with the small fluctuation and without a distinct decrease. Although the curves at high strain rates look as if the dominant softening mechanism is dynamic recovery, the microstructure observations indicate that DRX has taken place in all the deformed specimens. Fig.2 displays the microstructures at the center of the specimens before deformation and after deformation. Fig.2(a) shows the original micro- structure before deformation with the grain size of 90.0 μm. For initial grain size of 90.0 μm, the average grain sizes at the center of the specimens after deformation in Figs.2(b) and (c) are 60.0 and 29.7 μm, respectively. The grain sizes in Figs.2(b) and (c) are smaller than the original size of 90.0 μm, which indicates that the DRX has taken place. The stress—strain curve of GCr15 steel at 0.1 s-1 and 1 100 ℃ also exhibits a typical behavior of
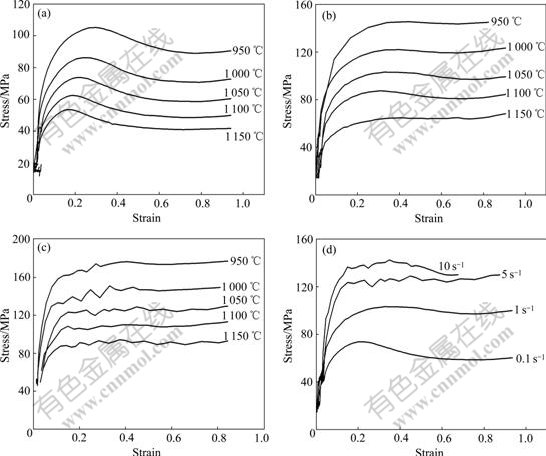
Fig.1 Stress—strain curves for GCr15 bearing steel at various temperatures and strain rates: (a) 0.1 s-1; (b) 1.0 s-1; (c) 5.0 s-1; (d) 1 050 ℃

Fig.2 Microstructures of GCr15 bearing steel under different conditions: (a) Before deformation; (b) 0.1 s-1, 1 100 ℃; (c) 10 s-1, 1 100 ℃
DRX (Fig.1). And the DRX grain size decreases with the increase of strain rate. It is clearly visible that the DRX grain is finer at the strain rate of 10.0 s-1, as shown in Fig.2(c).
3.2 Activation energy
The Arrhenius equation is widely used to describe the relationship among the strain rate, the flow stress, and the temperature at high temperature. It can also be shown with the Zener-Hollomon parameter (Z) as follows:
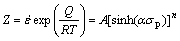 (1)
(1)
where Z is the Zener-Hollomon parameter; 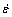 is the strain rate; Q is the activation energy; R is the ideal gas constant; T is the absolute temperature; n is the stress exponent; A and α are material dependent constants.
is the strain rate; Q is the activation energy; R is the ideal gas constant; T is the absolute temperature; n is the stress exponent; A and α are material dependent constants.
Eqn.(1) can be written in the following form:
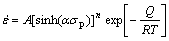 (2)
(2)
Taking natural logarithms and then partial derivative on both sides of Eqn.(2), we have
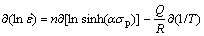 (3)
(3)
If T is a constant, Eqn.(3) can be rewritten as
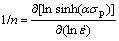 (4)
(4)
Fig.3 shows the variation of ln sinh(ασp) with 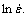 The value of n can be estimated from the reciprocal of slope of these curves, and its mean value is equal to 4.728 .
The value of n can be estimated from the reciprocal of slope of these curves, and its mean value is equal to 4.728 .
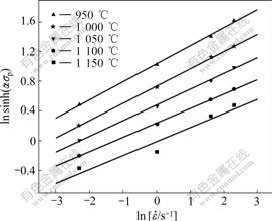
Fig.3 Plots of 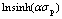 vs
vs 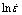 at different temperatures
at different temperatures
When 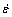 is a constant, Q can be calculated from Eqn.(3) as
is a constant, Q can be calculated from Eqn.(3) as
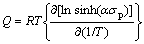 (5)
(5)
The curve slopes of 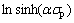 vs 1/T can be measured from Fig.4 as 8 920.85. Therefore, the mean activation energy is calculated as 351 kJ/mol from Eqn.(5).
vs 1/T can be measured from Fig.4 as 8 920.85. Therefore, the mean activation energy is calculated as 351 kJ/mol from Eqn.(5).
3.3 Determination of peak stress and peak strain
Fig.5 shows the dependence of peak stress on Z parameter. The hyperbolic sine function, Eqn.(1) is found to give a good fit to the data. The exact values of A and n can be obtained when 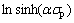 is plotted vs ln Z. The equation for peak stress as a function of Z is as
is plotted vs ln Z. The equation for peak stress as a function of Z is as

Fig.4 Plots of 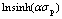 vs 1/T at different strain rates
vs 1/T at different strain rates
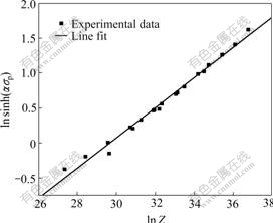
Fig.5 Effect of Z parameter on peak stress
follows:
σp=83.33sinh-1{[Z/(7.12×1012)]1/4.728} (6)
The peak strain is an important parameter. The critical strain at which dynamic recrystallization starts is linearly related to the peak strain and somewhat lower than it. The peak strain was considered a function of initial grain size D0, strain rate 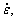 and temperature T by SUN and HAWBOLT[17]. It is revealed that the peak strain (εp) increases with an increase in strain rate and initial grain size, and it also increases with a decrease in temperature. Based on data analysis, the following equation is fitted for predicting εp, which is similar to the form of expression proposed by SUN and HAWBOLT[17].
and temperature T by SUN and HAWBOLT[17]. It is revealed that the peak strain (εp) increases with an increase in strain rate and initial grain size, and it also increases with a decrease in temperature. Based on data analysis, the following equation is fitted for predicting εp, which is similar to the form of expression proposed by SUN and HAWBOLT[17].
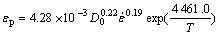 (7)
(7)
The values of εp calculated using the above equation were compared with experimental results in Fig.6. A good correlation between predictions and the measurements are illustrated.
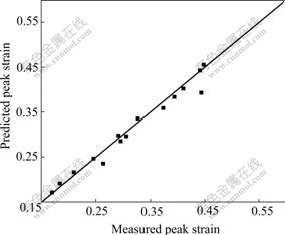
Fig.6 Correlation between measured peak strain and predicted peak strain
3.4 Flow stress model
LAASRAOUI and JONAS[18] analyzed the relationship between the strain hardening rate Θ and the stress σ, and the following equation was proposed to model flow stress in dynamic recovery region:
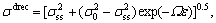 ε<εp (8)
ε<εp (8)
where σdrec is the flow stress when dynamic recovery is the only softening mechanism; σ0 is the initial stress and σss represents the saturation stress; Ω represents the ease of dynamic recovery.
To model softening due to dynamic recrystallization, an Avrami type equation was used. The fractional softening due to dynamic recrystallization is represented by:
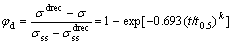 (9)
(9)
where φd is the volume fraction of dynamic recrystallization; 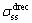 represents the steady state stress after recrystallization has progressed through the material; t is the isothermal holding time after the start of DRX; k is a constant time exponent; t0.5 is the time required for 50% recystallization to occur.
represents the steady state stress after recrystallization has progressed through the material; t is the isothermal holding time after the start of DRX; k is a constant time exponent; t0.5 is the time required for 50% recystallization to occur.
Eqn.(9) can be rewritten as follows to obtain a flow stress equation during dynamic recrystallization:
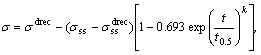
ε≥εp (10)
By regression analysis, the effects of strain rate and deformation temperature were summarized in a mathematical expression for predicting t0.5 for the GCr15 bearing steel as follows:
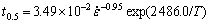 (11)
(11)
Fig.7 shows a comparison of flow stress curves predicted by the combination of Eqn.(8) and Eqn.(10) with experimentally measured values. A good agreement between the two can be observed. The model can give good description of stress—strain curves in the range of strain rate and temperature examined.
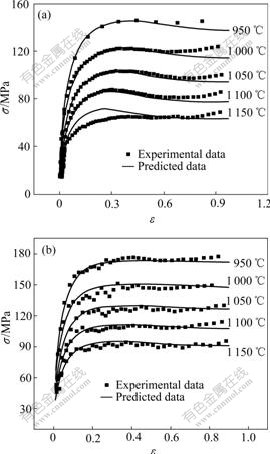
Fig.7 Comparison between model predictions and experimental results: (a)  =1 s-1; (b)
=1 s-1; (b)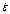 =5 s-1
=5 s-1
3.5 DRX grain size
In the present study, DRX grain sizes were measured under various deformation conditions. DRX grain size decreases with the increase of strain rate and the decrease of temperature. To model the dependence of the DRX grain size on temperature and strain rate, a relation was used[19-20]:
D=BZ-k (12)
where both B and k are constants. However, the analysis on measured data for GCr15 steel indicates that the strain rate exponent decreases with an increase in temperature. The form of Eqn.(12) is not suitable to predict the DRX grain size of the steel. Therefore, a complex expression correlating DRX grain size with temperature and strain rate was presented as follows:
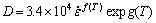 (13)
(13)
where both f(T) and g(T) are functions of temperature.
The DRX grain sizes calculated with the aid of the present model and the measured ones are shown in Fig.8. It can be observed that the model predictions are in good agreement with the measurements.
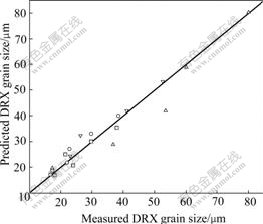
Fig.8 Comparison between measured and predicted DRX grain size
4 Conclusions
1) The hot deformation behavior of the GCr15 bearing steel is investigated by isothermal compressive tests at the temperature range of 950-1 150 ℃ and strain rate range of 0.1-10 s-1. Dynamic recrystallization occurs in all deformed specimens, even at strain rate of 10 s-1.
2) By regression analysis, in the temperature range of 950-1 150 ℃ and the strain rate range of 0.1-10 s-1, the mean activation energy and stress exponent for the GCr15 bearing steel are determined to be 351 kJ/mol and 4.728, respectively. The peak stress and the peak strain as functions of deformation parameters are generated.
3) The flow stress models in dynamic recovery region and dynamic recrystallization region are obtained. The volume fraction of dynamic recrystallization can be expressed by Avrami’s equation. The time for 50% recrystallization is determined by regression analysis. The equation for the dependence of DRX grain size on the strain rate and temperature is expressed as D=3.4×104? 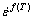 expg(T). The model predictions of flow stress and dynamic recrystallization grain size agree well with their measurements, respectively.
expg(T). The model predictions of flow stress and dynamic recrystallization grain size agree well with their measurements, respectively.
References
[1] PRASAD Y V R K, RAO K P. Mechanisms of high temperature deformation in electrolytic copper in extended ranges of temperature and strain rate [J]. Materials Science and Engineering A, 2004, A374: 335-341.
[2] SALEHI A R, SERAJZADEH S, YAZDIPOUR N. A study on flow behavior of A-286 superalloy during hot deformation [J]. Materials Chemistry and Physics, 2007, 101: 153-157.
[3] YUAN H, LIU W C. Effect of the  phase on the hot deformation behavior of Inconel 718 [J]. Materials Science and Engineering A, 2005, A408: 281-289.
phase on the hot deformation behavior of Inconel 718 [J]. Materials Science and Engineering A, 2005, A408: 281-289.
[4] GAO Hong, BARBER G C, CHEN Qi-an, LU Yu-qiu. High temperature deformation of a Fe-based low nickel alloy [J]. Journal of Materials Processing Technology, 2003, 142: 52-57.
[5] TENG Hao, YIN Zhi-min, ZHU Yuan-zhi, ZHOU Ke-chao, LI Zhi-you. Hot deformation behavior of Ni76Cr19AlTi superalloy [J]. Acta Metallurgica Sinica, 2006, 42(6): 629-634. (in Chinese)
[6] ZHANG Jun-hong, HUANG Bai-yun, HE Yue-hui, ZHOU Ke-chao, MENG Li-ping. Physical simulation of hot deformation of TiAl based alloy [J]. Journal of Central South University of Technology, 2002, 9(2): 73-76.
[7] EBRAHIMI R., ZAHIRI S H, NAJAFIZADEH A. Mathematical modelling of the stress—strain curves of Ti-IF steel at high temperature [J]. Journal of Materials Processing Technology, 2006, 171: 301-305.
[8] CABRERA J M, MATEO A, LLANES L, PRADO J M, ANGLADA M. Hot deformation of duplex stainless steels [J]. Journal of Materials Processing Technology, 2003, 143/144: 321-325.
[9] WANG Bing-xin, LIU Xiang-hua, WANG Guo-dong. Dynamic recrystallization behavior and microstructural evolution in a Mn-Cr gear steel [J]. Materials Science and Engineering A, 2005, A393: 102-108.
[10] IMBERT C A C, MCQUEEN H J. Dynamic recrystallization of A2 and M2 tool steels [J]. Materials Science and Engineering A, 2001, A313: 104-116.
[11] ELWAZRI A M, WANJARA P, YUE S. Dynamic recrystallization of austenite in microalloyed high carbon steels [J]. Materials Science and Engineering A, 2003, A339: 209-215.
[12] FERNANDEZ A I, URANGA P, LOPEZ B, RODRIGUEZ-ZBABE J M. Dynamic recrystallization behavior covering a wide austenite grain size range in Nb and Nb-Ti microalloyed steels [J]. Materials Science and Engineering A, 2003, A361: 367-376.
[13] WANG Bing-xin, WANG Guo-dong, LIU Xiang-hua, WANG Guo-dong. Dynamic recrystallization behavior in Mn-Cr gear steel [J]. Journal of Iron and Steel Research International, 2006, 13(2): 49-53.
[14] LI Xiong, ZHANG Hong-bing, RUAN Xue-yu, LUO Zhong-hua, ZHANG Yan. Kinetics for static recystallization after hot working of 0.38C-0.99Cr-0.16Mo steel [J]. Journal of Central South University of Technology, 2004, 11(4): 353-357.
[15] LI Zheng-sheng, FAN Zhi-li, ZHANG Guan-yun, DONG Zhang-gui, YANG Jian-mei, PENG Yi, WANG Shao-wen. Hot workability of high-carbon-chromium bearing steel [J]. Iron and Steel, 1996, 31(S): 61-66. (in Chinese)
[16] LIU Jing-rong, LI Bin, MAO Lei. High rate hot deformation and recrystallization of steel GCr15 [J]. Physics Examination and Testing, 1995(6): 7-11. (in Chinese)
[17] SUN W P, HAWBOLT E B. Comparison between static and dynamic recrystallization-an application to the hot rolling of steels [J]. ISIJ International, 1997, 37(10): 1000-1009.
[18] LAASRAOUI A, JONAS J J. Prediction of steel flow stresses at high temperatures and strain rates [J]. Metallurgical transactions A, 1991, 22A: 1545-1558.
[19] HODGSON P D. Microstructure modeling for property prediction and control [J]. Journal of Materials Processing Technology, 1996, 60: 27-33.
[20] KIM H Y, SOHN W H, HONG S H. High temperature deformation of Ti-(46-48)AL-2W intermetallic compounds [J]. Materials Science and Engineering A, 1998, A251: 216-225.
(Edited by YANG Hua)
Foundation item: Project(2001-122) supported by the Youth Science and Technology Elitist Foundation of Dalian, China
Received date: 2008-01-15; Accepted date: 2008-03-16
Corresponding author: ZHANG Li-wen, Professor, PhD; Tel: +86-411-84706087; E-mail: commat@student.dlut.edu.cn