基于IGA-RBF神经网络的导弹控制系统故障诊断
张文广1,史贤俊1,唐静2,肖支才1
(1. 海军航空工程学院 控制工程系,山东 烟台,264001;
2. 海军航空工程学院 研究生管理大队,山东 烟台,264001)
摘要:建立基于RBF神经网络的故障观测器模型以实现导弹控制系统的故障诊断,并针对传统RBF网络算法的不足,提出一种将改进的遗传算法(IGA)与正则化正交最小二乘法(ROLS)相结合的两级RBF学习方法。经过训练的RBF网络观测器与实际的系统并行工作,通过比较RBF观测器的估计输出和系统的实测输出产生残差,通过检测残差即可诊断系统是否出现故障。实验结果表明:基于IGA-RBF神经网络的故障观测器能够有效地实现导弹控制系统的故障诊断。
关键词:RBF神经网络;正交最小二乘法;遗传算法;故障诊断
中图分类号:TP183 文献标志码:A 文章编号:1672-7207(2011)S1-0870-06
Fault diagnosis based on RBFNN optimized by improved genetic algorithm in missile control system
ZHANG Wen-guang1, SHI Xian-jun1, TANG Jing2, XIAO Zhi-cai1
(1. Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China;
2. Graduate Students’ Brigade, Naval Aeronautical and Astronautical University, Yantai 264001, China)
Abstract: A failure observer based on RBF neural network was developed to realize the fault diagnosis of missile control system, and considering the shortage of traditional RBF learning method, a two-level learning method was proposed for designing radial basis function (RBF) network based on improved genetic algorithm optimization (IGA) and regularized orthogonal least squares (ROLS). The trained RBF observer worked concurrently with the actual system. Comparing the estimated output with the actual measurements, the residual signal was generated and then analyzed to report the occurrence of faults. The experimental results show that the failure observer based on the RBF neural network is effective in detecting the failure of the missile control system.
Key words: RBF neural network; orthogonal least squares algorithm; genetic algorithm; fault diagnosis
飞航导弹控制系统是飞航导弹的重要组成部分,其工作性能的好坏直接影响到整个导弹的技术状态和性能的发挥,甚至决定着导弹发射的成败。因此,对导弹控制系统进行故障诊断方法研究,提高其快速诊断能力就显得尤为重要。飞航导弹控制系统一般主要由控制部件、测量部件、舵机系统等部分组成,具有很多非线性元件,如电子放大器、齿轮等,因此,若采用基于模型的故障诊断方法则很难有效地对其进行准确的故障诊断。径向基函数(Radial basis function, RBF)网络是一种性能优良的三层前馈式神经网络,具有以任意精度逼近任意连续函数的能力,并被广泛应用于众多领域[1-2]。同传统的BP网络相比,RBF网络具有结构简单、收敛速度快、不存在局部极小的优点,同时具有很强的鲁棒性。鉴于这些特点,RBF神经网络辨识器可以很快地逼近被控对象的模型,并实时精确地跟踪模型的变化,所以可以通过RBF神经网络观测的变化进行系统故障检测。在此,本文作者首先建立了基于RBF神经网络的故障观测器模型以实现导弹控制系统的故障检测,并且针对传统RBF网络算法的不足,提出了一种将改进的遗传算法(Improved genetic algorithm, IGA)与正则化正交最小二乘法(Regularized orthogonal least squares, ROLS)相结合的两级RBF学习方法。经过训练的RBF网络观测器与实际的系统并行工作,通过比较RBF观测器的估计输出和系统的实测输出产生残差,通过检测残差即可诊断系统是否出现故障。实验结果表明,基于IGA-RBF神经网络的故障观测器能够有效地实现导弹控制系统的故障诊断。
1 RBF故障观测器设计
一般地,飞航导弹控制系统出现故障后,系统的数学模型参数会发生变化,因而可以采用基于故障观测的方法进行导弹控制系统的故障诊断。
假设导弹控制系统可以由下式描述
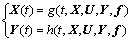 (1)
(1)
式中:X(t),Y(t),U(t)和f(t)分别表示系统的状态向量、测量的输出向量、控制输入向量和故障向量;g和h是非线性向量函数。
定义状态观测器为:
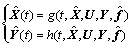 (2)
(2)
式中: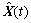 ,
,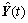 和
和 分别是X(t),Y(t)和f(t)的估计值。
分别是X(t),Y(t)和f(t)的估计值。
令状态误差为:
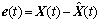 (3)
(3)
若对于f(t)=0和f(t)≠0,都有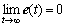 成立,则称状态观测器(式(2))为系统(式(1))的故障观测器。
成立,则称状态观测器(式(2))为系统(式(1))的故障观测器。
采用RBF神经网络来设计导弹控制系统的故障观测器,其结构图如图1所示。其中:yf和r分别为导弹控制系统舵机位置反馈输出的电压值和导弹控制系统的控制指令信号;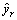 为RBF故障检测滤波器输出的电压估计值。
为RBF故障检测滤波器输出的电压估计值。
从图1可知:RBF神经网络属于三层前馈网络。这里采用多输入单输出即m个输入、n个隐节点、1个输出的RBF神经网络,其隐层作用函数采用Gaussian型径向基函数[3],即
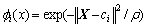 , i=1, 2, …, n (4)
, i=1, 2, …, n (4)
式中: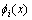 为第i个隐层节点的输出;X为输入样本,
为第i个隐层节点的输出;X为输入样本,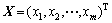 ;ci为第i个隐层节点的高斯核函数的中心,且与X具有相同的维数;
;ci为第i个隐层节点的高斯核函数的中心,且与X具有相同的维数; 为欧几里德(Euclidean)范数,ρ为函数的基宽度参数。
为欧几里德(Euclidean)范数,ρ为函数的基宽度参数。
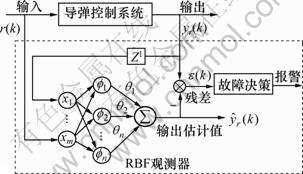
图1 基于RBF神经网络的故障观测器
Fig.1 Failure observer based on RBF neural network
选择归一化的RBF网络辨识器输入矢量为
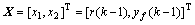 (5)
(5)
式中:r为导弹控制系统的控制指令信号;yf为导弹控制系统舵机输出的位置反馈信号。
RBF网络的输出估计值可定义为:
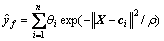 (6)
(6)
式中: 为第i个隐节点至输出的连接权值。
为第i个隐节点至输出的连接权值。
通过比较实际控制系统的舵机位置反馈输出电压测量值与网络输出估计值可产生残差,故定义辨识误差为:
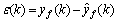 (7)
(7)
在正常情况下,实际系统和RBF神经网络输出相差不大,由于系统的噪声和干扰等因素,残差一般在零附近有波动。而当系统出现异常时,实际系统与RBF神经网络输出的残差不再为零。因此,利用故障观测器与实际系统的输出残差,可以通过适当逻辑判断实现导弹控制系统的故障检测。
2 正则化正交最小二乘(ROLS)法
假定共有N个训练样本,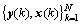 为其训练样本集,其中x(k)为网络的样本输入,y(k)为样本输入x(k)所对应的期望网络输出。设网络数据中心从样本输入数据中选取,将每个样本输入都选为RBF网络的数据中心,即ci=x(i) (1≤i≤N),当给定固定的基宽度参数ρ时,定义
为其训练样本集,其中x(k)为网络的样本输入,y(k)为样本输入x(k)所对应的期望网络输出。设网络数据中心从样本输入数据中选取,将每个样本输入都选为RBF网络的数据中心,即ci=x(i) (1≤i≤N),当给定固定的基宽度参数ρ时,定义
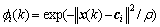 (8)
(8)
则期望的RBF网络输出可表示为
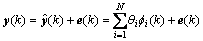 (9)
(9)
式中:e(k)表示网络实际输出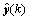 与期望输出y(k)的偏差。将式(9)写成矩阵形式:
与期望输出y(k)的偏差。将式(9)写成矩阵形式:
 (10)
(10)
式中: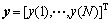 为输出向量;
为输出向量;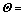
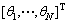 为权参数向量;
为权参数向量;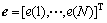 为残差向量;
为残差向量;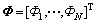 为回归矩阵,回归因子
为回归矩阵,回归因子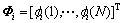 。
。
使用Gram-Schmidt法则对回归矩阵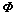 正交分解,即
正交分解,即
 (11)
(11)
 (12)
(12)
式中:A为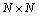 三角矩阵,它的主对角线元素为1,对角线下方为零;W为正交矩阵,它的任意两列向量wi和wj(i≠j)都满足
三角矩阵,它的主对角线元素为1,对角线下方为零;W为正交矩阵,它的任意两列向量wi和wj(i≠j)都满足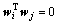 。于是,回归模型(10)可表达成
。于是,回归模型(10)可表达成
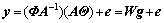 (13)
(13)
式中:正交权参数向量g满足
 (14)
(14)
ROLS算法[4]采用如下误差准则函数:
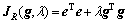 (15)
(15)
上式第二项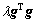 为正则化项,其中λ≥0为正则化系数。由
为正则化项,其中λ≥0为正则化系数。由 ,并经一些简单计算可得
,并经一些简单计算可得
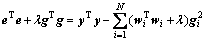 (16)
(16)
对式(16)进行标准化得
 (17)
(17)
因此,正则化后的误差下降率可定义为
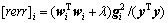 (18)
(18)
在此基础上,如同正交最小二乘 (Orthogonal least squares, OLS)算法[5]的前向回归过程选择重要的回归因子,当满足如下条件时,选择结束
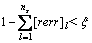 (19)
(19)
式中:0<ξ<1为给定的容许误差;ns为最终选出的回归因子个数。
对ROLS算法的正则化系数可以采用贝叶斯(Bayesian)方法[6]估计,给定一初始λ值,构造网络模型,并依次通过如下公式更新λ值
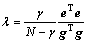 (20)
(20)
式中:
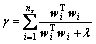 (21)
(21)
经过数次迭代后,就可找到一合适的λ值。
ROLS 算法中的正则化系数可以由贝叶斯方法迭代学习,但通过这种多次迭代梯度方法获取的正则化系数λ值一般情况下是一个局部最优值,只是在特定基宽度参数ρ下可能找到的较好的λ值。因此必须利用一种具有全局搜索能力的优化算法优选全局最佳的基宽度参数ρ和正则化系数λ。
3 基于改进遗传算法的参数优化
遗传算法是仿生物进化思想得出的一种自适应启发式全局搜索算法,它对于以往难于解决的函数优化问题、复杂的多目标规划问题、模式识别问题,神经网络的参数调整和优化问题等是最有效的方法之 一[7-8]。因此,这里采用遗传算法全局优化RBF网络的基宽度参数ρ和ROLS算法正则化系数λ,其基本思想是:在未知参数λ和ρ所有可能取值组合的可行解集合中找出最优解,使定义的适应度函数值最小。
为改善传统遗传算法的性能,下面从编码方式的选择、适应度函数的设计、初始种群的产生以及遗传操作等方面作了改进,从而对RBF网络的基宽度参数ρ和正则化系数λ进行优化。
3.1 编码方式选择
用遗传算法训练神经网络时,由于实数编码方式不需要对待优化参数进行编码及译码操作,而是直接把待优化参数连成一个实数向量的形式,提高了算法的收敛性及收敛速度。因此,本文采用实数编码方式,即把RBF网络的基宽度参数ρ和正则化系数λ编成染色体,把网络中这些参数的集合看成一个个体,并在初始化阶段采用完全随机方式产生初始群体。
3.2 适应度函数的设计
遗传算法中适应度函数的选取至关重要,直接影响到算法的收敛速度以及能否找到最优解。这里,可将数据集分为训练样本集和测试样本集,在给定初始值时,利用训练样本集通过ROLS算法设计RBF网络,当正则化后的误差下降率小于预先设定某一值时,算法回归因子的选择过程结束;计算测试样本集的期望输出与样本集实际网络输出之间的均方误差,此均方误差就是该个体的适应度值。
设Fr(x(k))为对测试样本的实际网络输出,Fs(x(k))为测试样本的期望输出,Ns为测试样本数,则适应度函数可选取为
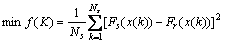 (22)
(22)
式中:K为个体 。
。
3.3 基因复制
赌轮选择机制是一种最基本、常用的选择机制。但为了保持算法的平稳性和全局收敛性,这里选用了最佳保留选择机制。首先按赌轮选择机制执行选择,然后将当前解中适应度最高的个体复制到下一代群体中,以保证遗传算法终止时得到的最后结果一定是历代出现过的最高适应度的个体。
3.4 自适应交叉操作
交叉采用实数编码遗传算法中的实值中间重组 法[9]。遗传算法中交叉概率Pc的选择对算法行为和性能都有着重要影响,为保证交叉的质量,交叉概率采用自适应方式产生,即交叉概率由进化程度控制。则改进的自适应交叉概率[10]由下式确定:
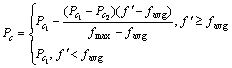 (23)
(23)
式中:fmax为群体中最大的适应度值;favg为每代群体的平均适应度值;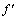 为要交叉的两个个体中较大的适应度值。这里,可取Pc1=0.9,Pc2=0.6。
为要交叉的两个个体中较大的适应度值。这里,可取Pc1=0.9,Pc2=0.6。
3.5 自适应变异操作
变异是对优选交叉后的个体进行的,为了保证变异的质量,采用改进后的自适应变异概率,其具体表达式为:
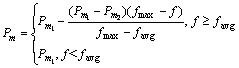 (24)
(24)
式中:fmax为群体中最大的适应度值;favg为每代群体的平均适应度值;f为要变异个体的适应度值。这里,可取Pm1=0.1,Pm2=0.001。
在参数优化中,基宽度参数ρ的搜索区间为 [0.000 1, 1],正则化系数λ的搜索区间为[0, 1]。遗传算法中的群体种数为50。
利用遗传算法进行优化而得到最优的λ和ρ参数后,便可由下级ROLS算法设计RBF网络。确定了RBF网络隐层节点数和数据中心后,网络从输入至输出将呈现线性结构,便可以采用简单的线性学习算法获得网络的输出权值。
4 系统故障决策
当导弹控制系统正常运行时,残差近似为高斯白噪声序列其均值近似为零,协方差阵为:
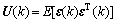 (25)
(25)
式中:ε(k)为系统的残差序列。
当状态估计协方差阵U(k)是时变的,随K的变化具有不同的统计特性。为此,定义另一随机变量
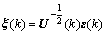 (26)
(26)
则ξ(k)近似为一零均值高斯白噪声随机向量。因U-1/2计算较不便,重新定义一随机变量:
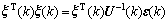 (27)
(27)
式中: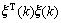 近似服从
近似服从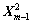 分布。因此,可得如下残差加权平方和的检测方法,令
分布。因此,可得如下残差加权平方和的检测方法,令
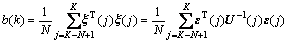 (28)
(28)
式中:N为数据窗长度。
当导弹控制系统正常运行时,b(k)的值较小;当系统发生突变故障时,b(k)的值较大,ξ(k)将不再满足白噪声特性,即得到如下的控制系统故障诊断方法:
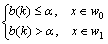 (29)
(29)
式中: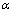 为某一阈值;w0为控制系统正模态;w1为控制系统的故障模态。
为某一阈值;w0为控制系统正模态;w1为控制系统的故障模态。
故障阈值的选择是故障诊断领域的一个难点。为减少由于传感器输出噪声和训练误差所引起的误报警,这里采用网络离线训练误差的最大值和噪声标准差4倍的和作为故障阈值。
5 仿真实验
为验证所提出的故障检测策略,对某型飞航式反舰导弹的控制系统进行在线实验研究。在导弹控制系统工作状态正常时,给系统输入一正弦测试信号,由遗传算法优化的RBF网络故障观测器根据大量样本训练后得到系统的估计输出。图2所示为正常情况下导弹控制系统舵机的位置反馈输出电压值和RBF神经网络估计值的残差曲线,RBF网络的输出同系统的输出电压差值不大,即在零附近波动。由此可以看出:本文遗传算法优化的RBF神经网络能够有效地逼近导弹控制系统的输出。
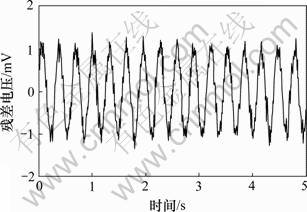
图2 系统正常时的输出残差曲线
Fig.2 Residual error under normal operating conditions
对某导弹控制系统的故障进行分析可知,电子放大器、齿轮等部分出现的故障在数学模型上表现为传递函数增益的突变,比如电子放大器的断路、齿轮的卡死等。下面模拟导弹控制系统的电子放大器故障,即可用PID控制器中的比例环节Kp增量模拟放大器增益漂移故障,则可得到如图3所示的输出残差电压曲线。
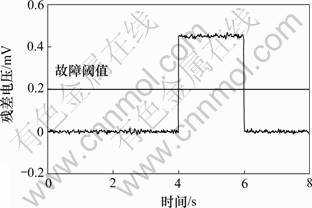
图3 系统故障时的输出残差曲线
Fig.3 Residual error under fault operating conditions
由图3可以看出:当电子放大器发生故障时,系统的输出电压和RBF网络的估计输出电压的残差不为零,残差幅值较大,大大地超过了故障阈值。因此,通过检测残差信号可以快速有效地诊断某导弹控制系统是否存在故障。
6 结论
(1) 该RBF 网络故障观测器仅能判别系统是否出现故障,即只能检测残差曲线的大小,而不能够准确地进行故障定位。
(2) 该RBF 网络观测器方法对导弹控制系统的故障比较敏感,是一种较好的快速诊断方法,且这种方法适用于多数非线性系统,在工程上具有较大的适用范围。
参考文献:
[1] LIU Hong-mei, OUYANG Pinge-chao, WANG Shao-ping. Fault detection based on RBF neural network in a hydraulic position servo system[C]//The 6th World Congress on Control and Automation. Dalian, China, 2006: 5708-5712.
[2] 彭继慎, 董晶. 基于RBF神经网络的控制系统传感器故障诊断方法[J]. 现代电子技术, 2009(12): 179-182.
PENG Ji-shen, DONG Jing. Method of control system sensor fault dignosis based on RBF neural network[J]. Journal of Modern Electronics Technique, 2009, 32(12): 179-182.
[3] 田景文, 高美娟. 人工神经网络算法研究及应用[M]. 北京: 北京理工大学出版社, 2006: 20-65.
TIAN Jing-wen, GAO Mei-juan. Artificial neural network algorithm research and application[M]. Beijing: Beijing Institute of Technology Press, 2006: 20-65.
[4] Chen S, Chng E S, Alkadhimi K. Regularized orthogonal least squares algorithm for constructing radial basis function networks[J]. Int J Contr, 1996, 64(5): 829-837.
[5] Chen S, Cowan C F N, Grant P M. Orthogonal least squares learning algorithm for radial basis function neural networks[J]. IEEE Trans Neural Networks, 1991, 2(2): 302-309.
[6] MacKay D J C. Bayesian interpolation[J]. Neural Comput, 1992, 4(3): 415-447.
[7] QIE Zhi-hong, WU Xin-miao, Furuta H, et al. The method of calculating hysteresis time of piezometric tube for earth-rock dam based on GA-RBF[C]//The 6th World Congress on Control and Automation. Dalian, China, 2006: 8523-8527.
[8] 黄友锐. 智能优化算法及其应用[M]. 北京: 国防工业出版社, 2008: 1-38.
HUANG You-rui. Intelligent optimization algorithms and application[M]. Beijing: National Defence Industry Press, 2008: 1-38.
[9] Srinivas M, Patnaik L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transations on SMC, 1994, 24(4): 656-667.
[10] 王小平, 曹立明. 遗传算法—理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002: 73-74.
WANG Xiao-ping, CAO Li-ming. Genetic algorithm—theory, application and software realization[M]. Xi’an: Xi’an Jiaotong University Press, 2002: 73-74.
(编辑 何学锋)
收稿日期:2011-04-15;修回日期:2011-06-15
通信作者:张文广(1979-),男,安徽蒙城人,硕士,讲师,从事飞行器自动测试技术研究;电话:0535-6635491,15653838915;E-mail: zwg30105@sina.com