DOI: 10.11817/j.issn.1672-7207.2015.11.042

考虑静压桩挤土应力影响的室内试验研究

王瑞彩¹，施建勇²，陈胜³，陈华杰⁴

(1. 河海大学 港口海岸与近海工程学院，江苏 南京，210098；

2. 河海大学 土木与交通学院，江苏 南京，210098；

3. 江苏省岩土工程公司，江苏 南京，210002；

4. 浙江省水利水电勘测设计院，浙江 杭州，310002)

摘要：通过GDS应力路径三轴仪进行饱和淤泥质粉质黏土的应变保持和剪切试验，模拟静压桩沉桩过程中及沉桩后桩周土体孔隙水压力、有效应力的变化以及剪切模量的变化。研究结果表明：桩周土体的超静孔隙水压力u与应变ε、初始应力σ₀有关；最大超静孔隙水压力u_max与应变ε之间近似双曲线分布关系；最大超静孔隙水压力u_max与初始应力σ₀之间、有效应力增量△σ_a′与初始应力σ₀之间近似直线变化关系；剪切模量G₅₀与距桩轴相对距离r/r₀之间近似双曲线分布，与深度有关；归一化后的剪切模量G₅₀/G_50∞与深度的关系不明显，仅与距桩轴相对距离r/r₀有关，7.5倍桩径之外的剪切模量G₅₀不再受到桩贯入的影响。

关键词：应变保持试验；剪切试验；超静孔隙水压力；有效应力增量；应变；初始应力；剪切模量

中图分类号：TU411             文献标志码：A         文章编号：1672-7207(2015)11-4292-08

Laboratory test study on compacting stress effect of jacked pile

WANG Ruicai¹, SHI Jianyong², CHEN Sheng³, CHEN Huajie⁴

(1. College of Harbour, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China;

2. College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China;

3. Geo-technical Engineering Company of Jiangsu Province, Nanjing 210002, China;

4. Zhejiang Design Institute of Water Conservancy and Hydroelectric Power, Hangzhou 310002, China)

Abstract: Based on the strain-holding test and shearing test of saturated muddy silty clay by using GDS stress path triaxial apparatus, the changes of effective stress, excess pore water pressure and shear modulus of soil around the pile were simulated during and after pile jacking respectively. The results show that excess pore water pressure of soil around the pile is related to strain value and initial stress. Relationship between maximum excess pore water pressure and strain indicates approximate hyperbola distribution relationship. Furthermore, relationships between maximum excess pore water pressure and initial stress as well as effective stress increment and initial stress display approximately linear relationship. The approximate hyperbola distribution is revealed between shear modulus and normalized radial distance. Shear modulus also has some relationship with depth. The normalized shear modulus is related to normalized radial distance, while it has no obvious relationship with depth. The shear modulus is not affected by pile jacking beyond 7.5 times pile diameter.

Key words: strain-holding test; shear test; excess pore water pressure; effective stress increment; strain; initial stress; shear modulus

静压桩是一种挤土桩，当桩压入饱和黏性土中后，其周围土体受到较大的挤压变形，引起相当大的超静孔隙水压力，随着超静孔隙水压力的消散，土体中有效应力增加，土体性质发生相应的变化。Seed等^[1]进行的现场试验结果表明：由于桩的置入产生了很大的超静孔隙水压力，甚至超过了初始的上覆压力；Roy等^[2]的现场试验结果表明：由于桩的贯入，桩周土体中产生的超静孔隙水压力随着距桩轴距离的增加而急剧降低，在8倍桩径之外超静孔隙水压力几乎为零；Hunt等^[3-12]的试验结果都显示了桩的贯入会产生相当大的超静孔隙水压力。关于挤土作用对桩周土体力学性质的影响，Randolph等^[13]认为桩周土体的剪切模量沿桩轴可以看成是随深度呈线性增加的变化趋势，在径向沉桩瞬间桩周土体的剪切模量降低，待土体固结完成后，一定范围内桩周土体的剪切模量会超过原状土的剪切模量；陈海丰^[14]运用英国剑桥大学编制的Crisp程序，对饱和砂土中的沉桩效应进行了有限元分析，并进行了饱和砂土的三轴试验，得出了桩周土体固结完成后剪切模量是初始剪切模量2~3倍的结论。Fioravante等^[15]在Fucino黏土中做了大量的保持旁压力不变的压力保持试验和保持旁压体积不变的应变保持试验。压力保持试验与挤土总应力不发生变化的假设相一致，结果显示桩周土体发生变形，旁压应变不断增大；应变保持试验与桩挤土结束后的位移边界条件相似，符合静压桩的压桩实际情况，结果显示在超静孔隙水压力消散过程中作用在桩壁上的压力不断减小。为考虑挤土应力的影响，分析静压桩沉桩过程中和沉桩后超静孔隙水压力和有效应力的变化规律及贯桩对桩周土体力学性质的影响，本文作者利用GDS应力路径三轴仪进行室内三轴应变保持试验和剪切试验，模拟沉桩过程及沉桩后挤土位移不变条件下，桩周土体内的超静孔隙水压力和有效应力的变化过程以及桩周土体固结后剪切模量的变化情况。

1  室内三轴应变保持试验

1.1  试验的应力路径与过程

Baligh等^[16-17]研究桩从开始贯入到结束过程中桩周土体的应力路径，发现水平应力逐渐大于竖向应力，发生了主应力轴旋转。由于用应力路径三轴仪全面模拟桩贯入过程的应力路径是困难的，为便于研究，经过对应力路径进行简化，本文试验采用以下的应力路径：首先使土样在K₀条件下固结，然后在不排水条件下不断增大水平应力(模拟静压桩沉桩过程中对桩周土体的挤压作用)，达到某一给定的应变后保持挤土位移不变，打开排水阀在排水条件下观测有效应力及孔隙水压力的变化(模拟静压桩沉桩结束后桩周土体的固结过程)，如图1和图2所示。其中为水平应力，为竖向应力，K₀为静止侧压力系数。

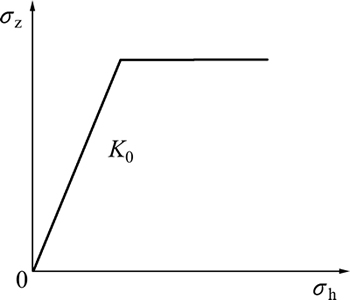
图1  K₀固结和应变施加阶段应力路径

Fig. 1  Stress path of K₀ consolidation and strain-applied stage

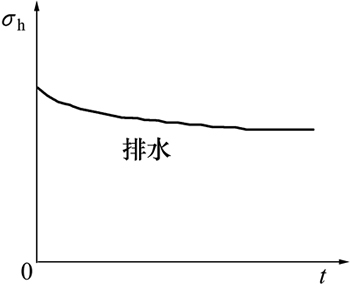
图2  排水条件下挤土应力随时间变化

Fig. 2  Variation of soil compaction stress with time

利用GDS应力路径三轴仪进行室内三轴应变保持试验时，为了在GDS上实现保持挤土位移不变的条件，试验时施加的轴向应力为地基土的水平应力、施加的径向应力采用地基土的竖向应力，相当于将地基中的大小主应力转动90°，移置到GDS三轴试验仪上。试验时，首先对试样进行饱和，然后进行K₀固结，待K₀固结完成后在某一初始应力状态下对土样施加应变，进行不排水条件下的应变施加试验，模拟静压桩贯桩过程中对桩周土体的挤压作用；待试样达到给定的应变值后保持应变不变，进行排水条件下的应变保持试验，模拟静压桩沉桩结束后桩周土体的固结过程，测定孔隙水压力和有效应力的变化情况；待应变保持结束后(超静孔隙水压力消散完毕)，保持径向压力不变，增大轴向压力进行不排水剪切试验，直至试样破坏，测定土体固结完成后的剪切模量，模拟桩贯入土体后引起的桩周土体剪切模量的变化。

1.2  试样

本试验所用土样取自昆山某质检中心场地，该场地地貌形态单一。根据勘探资料，场区自然地面下最大勘探深度70.45 m以内为第四纪沉积物，主要由饱和黏性土及粉土组成。按其物理力学性质及工程特性，从上到下可分为5个工程地质层。试验所用土样取自第3层淤泥质粉质黏土层，该层土的物理力学性质指标见表1。

本试验采用原装试样进行试验，采用标准试样的直径×高度为39.1 mm×80 mm。经过常规的K₀固结试验，得到平均K₀为0.52。

1.3  试验内容

考虑到不同深度处的初始应力不同，在同一深度处，距桩轴的距离不同，沉桩时沿径向的挤土应变也不同。为模拟沉桩过程中及沉桩后不同深度处以及距桩轴不同距离处的孔隙水压力和应力变化，本次试验选取5组不同的初始应力，分别施加5组不同的应变，共进行25组试验，试验加荷计划如表2所示。

2  试验结果与分析

2.1  应变施加试验结果与分析

应变施加阶段模拟贯桩过程中对桩周土体的挤压作用。为找出贯桩过程中桩周土体应力和孔隙水压力随时间的变化规律，点绘初始应力状态为72.9 kPa的试样在施加1%和4%应变时的总应力()、有效应力(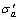)和超静孔隙水压力(u)随应变施加时间(t)的变化曲线，如图3和图4所示。

表1  试验用土样的物理力学性质指标

Table 1  Physical property indexes of test site

表2  试验加荷计划

Table 2  Loading schedule of test

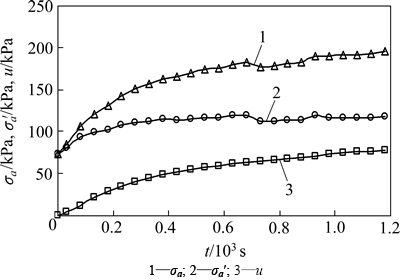
图3  应变施加阶段D72.9-1试样的σ_a，σ_a′和u与t关系曲线

Fig. 3  Relation curves of σ_a, σ_a′ and u with t for D72.9-1 sample during loading stage

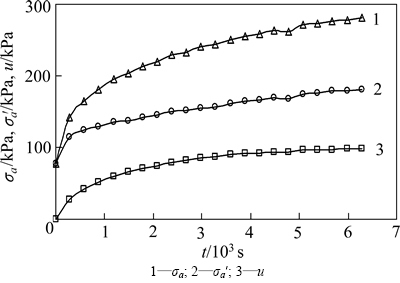
图4  应变施加阶段D72.9-4试样的σ_a，σ_a′和u与t关系曲线

Fig. 4  Relation curves of σ_a, σ_a′ and u with t for D72.9-4 sample during loading stage

从图3和图4可以看出：在应变施加过程中，总应力、有效应力和超静孔隙水压力都随应变施加时间的增加而增加。初始应力为72.9 kPa的试样施加1%应变时，其总应力、有效应力和超静孔隙水压力的增量分别是初始应力的1.67，0.63和1.1倍，而施加4%应变的试样，其总应力、有效应力和超静孔隙水压力的增量则分别增加到了2.84，1.49和1.35倍初始应力，相对于1%应变下的增量有了很大的增加，说明总应力、有效应力和超静孔隙水压力增量随着施加应变的增大而增大。

现场沉桩过程中，桩周土体受到不同程度的挤压，受挤压程度与距离桩身的远近有关，距离桩身越近受挤压程度越大。图3和图4反映出了现场沉桩过程中，桩周土体总应力、有效应力和超静孔隙水压力随着距桩身距离的变近而变化的趋势。

应变施加过程中的最大超静孔隙水压力与应变之间关系如图5所示。从图5可以看出：在相同的初始应力条件下，随着应变的增加，最大的超静孔隙水压力呈增加趋势，两者之间近似双曲线分布。对于某一初始应力，点绘ε/u_max与ε关系曲线，从而得到图6所示的关系曲线。从图6可以看出：ε/u_max与ε之间呈线性关系，可以表示为ε/u_max=k_u1ε+a，其中k_u1为拟合直线的斜率，表示最大超静孔隙水压力渐近值的倒数，随着初始应力的增加而呈现降低的趋势。即：随着初始应力的增加，最大超静孔隙水压力的渐近值在增大，从初始应力状态为18.7 kPa的渐近值26 kPa增加到初始应力状态为100.1 kPa的渐近值160 kPa。

图5和图6反映出沉桩过程中对于同一贯入深度，桩周土体产生的最大超静孔隙水压力随距桩轴距离的变近而逐渐增大，其中图5和图6中Fioravante曲线为文献[15]中当渗透系数k_v=k_h=10^-10 m/s时超静孔隙水压力与应变关系的曲线，可以看出Fioravante的计算曲线与本文的试验曲线呈现很好的一致性，说明本文试验结果是可信的。

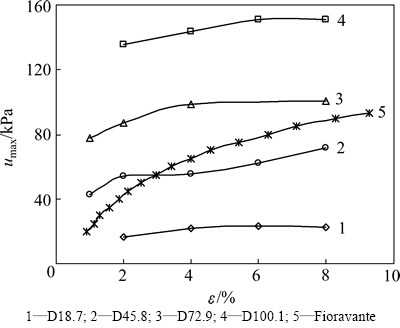
图5  应变施加阶段u_max与ε关系曲线

Fig. 5  Relation curves of u_max with ε during loading stage

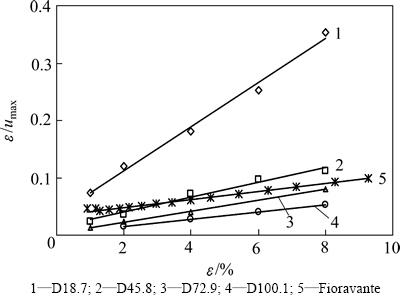
图6  应变施加阶段ε/u_max与ε关系曲线

Fig. 6  Relation curves of ε/u_max with ε during loading stage

应变施加过程中的最大超静孔隙水压力与初始应力之间关系如图7所示。从图7可以看出：在相同的应变条件下，超静孔隙水压力随着初始应力的增加而增加，呈近似直线变化关系，可以表示为u_max=k_u2σ₀+b。对于不同的应变条件，直线变化的斜率k_u2不同，k_u2随着应变的增加而增大，从1%应变状态的1.1左右变化到8%应变状态的1.5左右。其中图7中Boring-1，Boring-2和Boring-3曲线为文献[3]和[5]中进行的现场原位测试资料，钻孔分别距桩外壁0.6，1.2和2.1 m。可以看出文献[3]和[5]中的原位测试试验结果也符合本文提出的u_max=k_u2σ₀+b的线性变化关系。

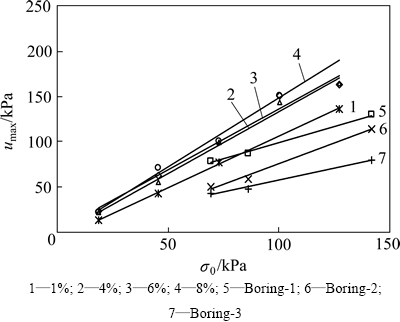
图7  应变施加阶段u_max与σ₀关系曲线

Fig. 7  Relation curves of u_max with σ₀ during loading stage

应变施加过程中的有效应力增量与初始应力之间关系如图8所示。从图8可以看出：在相同的应变条件下，有效应力增量随着初始应力的增加而增加，呈近似直线变化关系，可以表示为△σ_a′=k_σ1σ₀+c。对于不同的应变条件，直线变化的斜率k_σ1不同，k_σ1随着应变的增加而增大，从1%应变处的0.5左右增加到8%应变处的1.2左右。

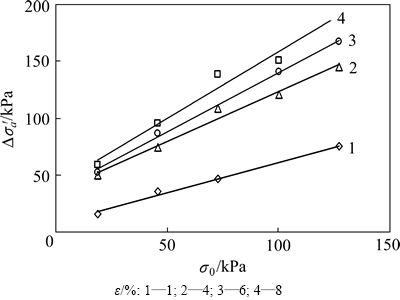
图8  应变施加阶段△σ_a′与σ₀关系曲线

Fig. 8  Relation curves of △σ_a′ with σ₀ during loading stage

2.2  应变保持试验结果与分析

应变施加结束后试样进入应变保持阶段，对应于现场的桩贯入后桩周土体的超静孔隙水压力消散、有效应力提高、桩周土体性质发生变化阶段。图9和图10所示分别为初始应力为127.2 kPa的试样应变保持在1%和4%条件下的总应力、有效应力和超静孔隙水压力随应变保持时间的变化曲线。

从图9和图10可以看出：随着应变保持时间的增加，总应力和超静孔隙水压力逐渐减小，有效应力逐渐增加，最后趋于稳定；在初始应力相同的情况下，应变大的试样其总应力和超静孔隙水压力的降低值相对较大，有效应力增量相对较大。反映出现场沉桩结束后，桩周土体中的超静孔隙水压力逐渐消散、有效应力逐渐提高的变化过程。

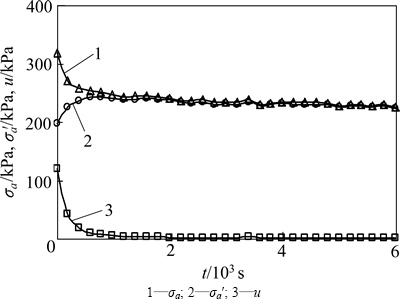
图9  应变保持阶段D127.2-1试样σ_a，σ_a′和u与t关系曲线

Fig. 9  Relation curves of σ_a, σ_a′ and u with t for D127.2-1 sample during strain-holding stage

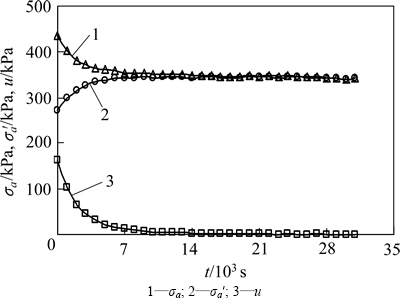
图10  应变保持阶段D127.2-4试样σ_a，σ_a′和u与t关系曲线

Fig. 10  Relation curves of σ_a, σ_a′ and u with t for D127.2-4 sample during strain-holding stage

应变保持阶段的有效应力增量与初始应力之间关系如图11所示。从图11可以看出：在应变相同的条件下，有效应力增量随着初始应力的增加而增加，呈近似直线变化关系，可以表示为：△σ_a′=k_σ2σ₀+d。直线变化的斜率k_σ2随着应变的改变有所不同，在1%应变处直线变化的斜率k_σ2为0.36，与4%，6%和8%应变处的斜率k_σ2大约为0.70有较大的差别。这是由于施加1%应变的试样受到的挤压程度较小，产生的超静孔隙水压力相对较小，因此，在应变保持阶段由于超静孔隙水压力消散而产生的有效应力增量也较小。

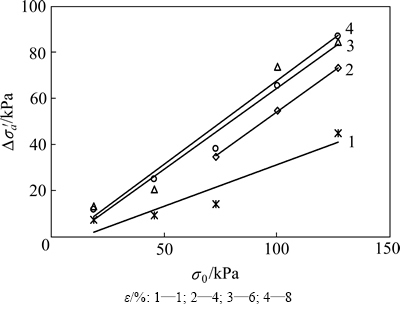
图11  应变保持阶段△σ_a′与σ₀关系曲线

Fig. 11  Relation curves of △σ_a′ with σ₀ during strain-holding stage

从图8和图11可以看出：应变施加阶段引起的有效应力增量是应变保持阶段由于超静孔隙水压力消散而引起的有效应力增量的2~3倍，反映出现场沉桩过程中桩周土体由于受到挤压而产生有效应力的增量，比沉桩结束后由于超静孔隙水压力消散而引起的有效应力增量要大得多。

2.3  剪切试验结果分析

在应变保持阶段结束后，保持径向压力不变，增大轴向压力进行不排水剪切试验，直至试样破坏，测定土体剪切模量，用以模拟桩贯入土体后所引起的桩周土体剪切模量的变化情况。

Houlsby等^[18]给出了剪切模量的4种定义：初始切线模量G₀、对应于一半破坏剪应力的割线模量G₅₀、卸载再加载模量G_ur和在小应变下的动剪切模量G_max。本次试验采用割线模量G₅₀作为土体的剪切模量。根据试验数据，得到各试样的剪切模量与应变之间的关系曲线，如图12所示。

从图12可以看出：在初始应力状态相同的条件下，剪切模量G₅₀随着应变的增大而增大，8%应变处的剪切模量是1%应变处的4~6倍，由此可以看出由于桩的贯入对桩周土体的挤压以及桩周土体的固结，引起了桩周土体性质的改变。

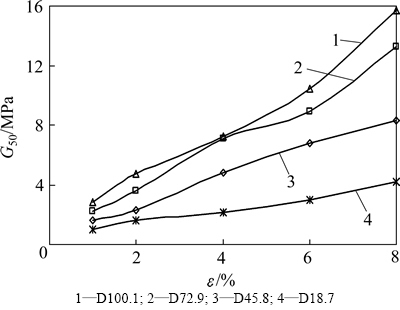
图12  G₅₀与ε关系曲线

Fig. 12  Relation curves of G₅₀ with ε

从图12还可以看出：在应变相同的条件下，不同的初始应力对于剪切模量增长也是有影响的，剪切模量G₅₀随着初始应力的增大而增大，初始应力为100 kPa试样的剪切模量是18.7 kPa试样的3.0~3.5倍。陈胜^[19]根据圆柱孔扩张理论的位移解答，得出试验的应变、剪切模量与对应的距桩轴相对距离的关系，如表3所示，其中r₀为贯入桩的半径，r为桩周土体中某一点距桩轴中心的距离。

点绘剪切模量G₅₀与距桩轴相对距离r/r₀的关系曲线，如图13所示。从图13可以看出：无论初始应力如何，剪切模量G₅₀随着距桩轴相对距离r/r₀的增加而呈现双曲线的变化趋势，拟合图13的双曲线，得到在r/r₀→∞时的剪切模量G_50∞，即是原位状态下的剪切模量。

对剪切模量G₅₀进行归一化处理，即：将相应位置处的G₅₀除以原位状态下的G_50∞。点绘归一化的剪切模量G₅₀/G_50∞与距桩轴相对距离r/r₀的关系曲线，如图14所示。从图14可以看出：归一化后的剪切模量G₅₀/G_50∞随着距桩轴相对距离r/r₀的增加呈现双曲线变化，此时随深度的变化已经不明显，可以将经过归一化后的剪切模量仅仅看作是与距桩轴相对距离有关，而与深度无关。其中图14中的陈海丰曲线为文献[14]中进行的饱和砂土的三轴实验结果，Kraft曲线为文献[20]中在计算理论t-z曲线时假定的归一化剪切模量G₅₀/G_50∞沿径向变化的趋势。可以看出文献[14]的试验结果和文献[20]的计算假定与本文试验结果的变化趋势基本相同。

将归一化的剪切模量G₅₀/G_50∞与r₀/r点绘到同一坐标系中，如图15所示。从图15可以看出：归一化

的剪切模量G₅₀/G_50∞与r₀/r呈现很好的线性关系，两者之间的拟合关系可以表示为

G₅₀/G_50∞=18.75r₀/r-1.49            (1)

当G₅₀/G_50∞=1时，表示桩贯入土体后对土体性质不产生影响。将G₅₀/G_50∞=1代入式(1)中，可得到桩周土体受桩贯入的影响范围r/r₀=7.5，即在7.5倍桩径之外的土体性质不再受到桩贯入的影响。Kraft等^[20]在计算理论t-z曲线时，假定归一化剪切模量G₅₀/G_50∞沿径向变化的趋势与本文所得的结论基本一致，其所采用的影响范围是r/r₀=5。

表3  应变、剪切模量与距桩轴相对距离对应关系

Table 3  Relationship between strain values, shear modulus and relative distance from pile shaft

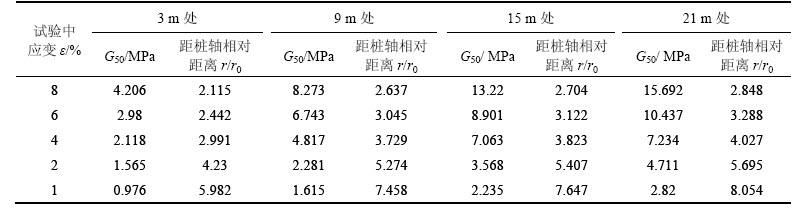
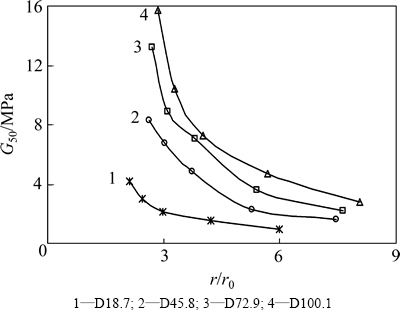
图13  G₅₀与r/r₀关系曲线

Fig. 13  Relation curves of G₅₀ with r/r₀

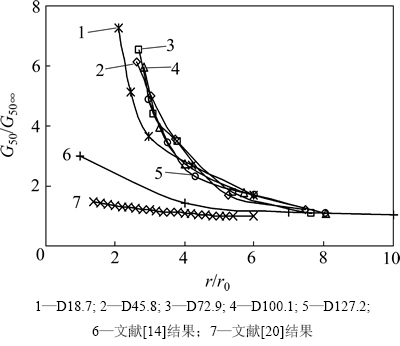
图14  G₅₀/G_50∞与r/r₀关系曲线

Fig. 14  Relation curves of G₅₀/G_50∞ with r/r₀

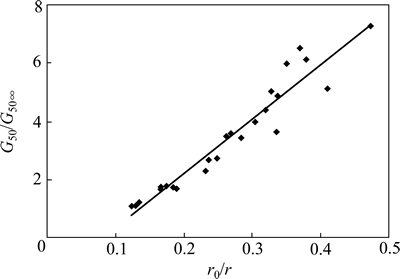
图15  G₅₀/G_50∞与r₀/r关系曲线

Fig. 15  Relation curve of G₅₀/G_50∞ with r₀/r

3  结论

1) 应变施加过程中的最大超静孔隙水压力与应变之间近似双曲线分布，可以用x/y=kx+a的形式表示，k为最大超静孔隙水压力渐近值的倒数，随着初始应力的增加而呈现降低的趋势。

2) 无论是应变施加过程中的最大超静孔隙水压力与初始应力之间、有效应力增量与初始应力之间还是应变保持阶段的有效应力增量与初始应力之间都近似线性变化关系，可以用y=kx+b的形式表示，对于不同的应变条件，直线变化的斜率k不同，基本上随着应变的增加而增大。

3) 剪切模量随着距桩轴相对距离的增加而呈现双曲线的变化趋势，与深度有关；归一化后的剪切模量与深度的关系不明显，随着径向距离的变化而变化，在7.5倍桩径之外土体的剪切模量不再受到桩贯入的影响。

参考文献：

[1] Seed H B, Reese L C. The action of soft clay along friction piles[J]. Transactions of the American Society of Civil Engineers, 1957, 122(1): 731-754.

[2] Roy M, Blanchet R, Tavenas F, et al. Behavior of a sensitive clay during pile driving[J]. Canadian Geotechnical Journal, 1981, 18(2): 67-85.

[3] Hunt C E, Pestana J M, Bray J D, et al. Effect of pile installation on static and dynamic properties of soft clays[C]// Mayne P W. Innovations and Applications in Geotechnical Site Characterization. Denver: American Society of Civil Engineers, 2000, 258(97): 199-212.

[4] Hwang J H, Liang N, Chen C H. Ground response during pile driving[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(11): 939-949.

[5] Pestana J M, Hunt C E, Bray J D. Soil deformation and excess pore pressure field around a closed-ended pile[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2002, 128(1): 1-12.

[6] Ladanyi B, Longtin H. Short- and long-term sharp cone tests in clay[J]. Canadian Geotechnical Journal, 2005, 42(1): 136-146.

[7] 周火垚, 施建勇. 饱和软黏土中足尺静压桩挤土效应试验研究[J]. 岩土力学, 2009, 30(11): 3291-3296.

ZHOU Huoyao, SHI Jianyong. Test research on soil compacting effect of full scale jacked-in pile in saturated soft clay[J]. Rock and Soil Mechanics, 2009, 30(11): 3291-3296.

[8] Yang J, Tham L G, Lee P K K, et al. Observed performance of long steel H-piles jacked into sandy soils[J]. Journal of Geotechnical and Geoenvironmental Engineering. 2006, 132(1): 24-35.

[9] LIU Junwei, ZhANG Zhongmiao, YU Feng, et al. Case history of installing instrumented jacked open-ended piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2012, 138(7): 810-820.

[10] 张忠苗, 谢志专, 刘俊伟, 等. 粉土与淤质互层土中管桩压入过程孔隙水压力试验研究[J]. 岩土工程学报, 2010, 32(增刊2): 533-536.

ZHANG Zhongmiao, XIE Zhizhuan, LIU Junwei, et al. Experimental study on pore pressure during pile driving in silty soil with muchy soil interbed[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(Suppl 2): 533-536.

[11] 雷华阳, 李肖, 陆培毅, 等. 管桩挤土效应的现场试验和数值模拟[J]. 岩土力学, 2012, 33(4): 1006-1012.

LEI Huayang, LI Xiao, LU Peiyi, et al. Field test and numerical simulation of squeezing effect of pipe pile[J]. Rock and Soil Mechanics, 2012, 33(4): 1006-1012.

[12] WANG Ruicai, SHI Jianyong, CHEN Shen, et al. Experimental study on the time effect of the jacked pile[C]// Applied Mechanics and Materials. Switzerland: Trans Tech Publications, 2013: 125-129.

[13] Randolph M F, Wroth C P. Analysis of deformation of vertically loaded Piles[J]. Journal of the Geotechnical Engineering Division, 1978, 104(12): 1465-1488.

[14] 陈海丰. 考虑沉桩挤土效应的单桩极限承载力研究[D]. 南京: 河海大学土木与交通学院, 2005:32-42.

CHEN Haifeng. Research on ultimate carrying capacity of single pile considering the effect of soil compaction during pile driving[D]. Nanjing: Hohai University. College of Civil and Transportation Engineering, 2005:32-42.

[15] Fioravante V, Jamiolkowski M, Lancellotta R. An analysis of pressuremeter holding tests[J]. Géotechnique, 1994, 44(2): 227-238.

[16] Baligh M M. Strain path method[J]. Journal of Geotechnical Engineering, 1985, 111(9): 1108-1136.

[17] White D J, Bolton M D. Displacement and strain paths during plane stain model pile installation in sand[J]. Geotechnique, 2004, 54(6): 375-397.

[18] Houlsby G T, Wroth C P. The variation of shear modulus of a clay with pressure and over-consolidation ratio[J]. Soil and Foundations, 1991, 31(3): 138-143.

[19] 陈胜. 考虑挤土效应的桩基承载力室内试验研究[D]. 南京: 河海大学土木与交通学院, 2010: 52-60.

CHEN Sheng. Research on ultimate carrying capacity of single pile considering the effect of soil compaction based on laboratory tests[D]. Nanjing: Hohai University. College of Civil and Transportation Engineering, 2010: 52-60.

[20] Kraft L M, Ray R P, Kagawa T. Theoretical t-z curves[J]. Geotechnical Engineering Division, 1981, 107(11): 1543-1561.

(编辑  杨幼平)

收稿日期：2014-11-29；修回日期：2015-02-14

基金项目(Foundation item)：中央高校基本科研业务费专项资金资助项目(2009B10514) (Project(2009B10514) supported by the Fundamental Research Funds for the Central Universities)

通信作者：施建勇，博士，教授，从事岩土工程研究；E-mail: soft-ground@hhu.edu.cn