基于改进响应面的桥梁抗弯刚度修正

代汉超，石雪飞，阮欣

(同济大学 桥梁工程系, 上海，200092)

摘要：根据响应面法(RSM)的应用条件，从工程应用角度研究响应面法改进方法及桥梁抗弯刚度修正中确定设计空间大小的一般原则。利用单因素试验法，令抗弯刚度在初始设计值的基础上产生单位改变量，考察目标函数对应的改变量，建立两者之间的线性函数关系，以初始有限元模型的目标函数值和对应实测值的差值为目标，通过优化算法，使待修正参数的设计空间快速逼近最优区域。在优化的设计空间里建立响应面模型对桥梁结构抗弯刚度进行修正。数值算例和三跨连续梁实桥静载试验算例证明：该方法显著地提高了基于响应面的桥梁结构抗弯刚度修正的精度。

关键词：响应面；单因素试验设计；设计空间优化；桥梁抗弯刚度修正

中图分类号：TU311              文献标志码：A         文章编号：1672-7207(2014)07-2387-07

Bending stiffness updating of bridge structures based on improved response-surface method

DAI Hanchao, SHI Xuefei, RUAN Xin

(Department of Bridge Engineering, Tongji University, Shanghai 200092, China)

Abstract: According to the application conditions of response surface method (RSM), an improved response-surface method was proposed from the view point of engineering application. In addition, a general rule to decide the boundary of design space in updating bending stiffness of bridge structures was presented. In the one-factor experimental design, linear functions were established which expressed the change of correction parameters and that of objective functions. Optimal algorithm was used to reduce the gap between the linear functions’ results and the differences of initial FEM values and measured values. In this way, the design space approached to the optimal space rapidly. Then response surface method of bridge structures was constructed to update the bending stiffness. The proposed procedure was illustrated by a numerical beam and a three-span continuous bridge tested under static load conditions.

Key words: response surface; one-factor experimental design; optimization of design space; bending stiffness updating of bridge

桥梁结构可以看成是一个刚度、质量和阻尼矩阵组成的力学系统。其中桥梁刚度参数是桥梁承载能力、病害成因、抗震防灾能力分析评估的重要参数，事实上许多损伤识别问题最后都归结为刚度修正^[1-3]，解决大跨径预应力混凝土梁桥的主跨长期下挠过量和梁体开裂等关键问题^[4]也涉及到对桥梁抗弯刚度的修正。因此，桥梁刚度修正是有限元模型修正^{[1, 5]}的一个重要内容。而基于响应面法(RSM)的有限元模型修正是近年来一个研究热点，它是以显式的响应面模型逼近设计参数与目标函数间复杂的隐式函数关系，得到简化的结构模型(Meta-model)^[6-8]，从而代替原有限元模型，在其基础上进行复杂计算，实现优化修正和预测响应等。尽管基于响应面方法的结构有限元模型修正^[9-12]取得了一些研究成果，但如何提高响应面模型的精度仍有待研究。为此，本文作者介绍一种基于静力响应面的桥梁抗弯刚度修正技术，并从工程应用的角度对响应面法进行改进，对桥梁抗弯刚度修正中确定试验设计空间大小的一般原则进行探讨。

1  基于响应面法的有限元模型修正

基于响应面的有限元模型修正的主要步骤包括：样本选取、响应面的拟合、回归方程及系数的显著性检验和构建优化函数进行有限元模型修正。

(1) 基于试验设计的样本选取。样本的选取关系到响应面的精度和试验成本，试验设计的本质是在设计空间挑选出合适的代表点。正交试验设计和中心复合设计^[13]是基本的试验设计方法，本文进行2水平正交试验设计。正交试验对于全面试验来说是一种部分试验，但对于其中任何2个因素却是具有等量重复的全面试验^[14]。

(2) 响应面的拟合。对大多数工程问题来说，一阶或二阶多项式模型可以满足工程要求^[15]，一阶模型可表示为

    (1)

写成矩阵形式为Y=XB+e。

式中：β₀和β_i为待估计的回归系数；x_i为待修正参数；Y为所有响应构成的向量；e为相应的误差向量；X为修正参数矩阵；B为所有回归系数组成的矩阵，常由最小二乘法求解：。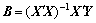

(3) 显著性检验。一般来说，对于多个响应面模型和较复杂模型，常应用R²检验^[13]和相对均方根误差检验^[16]。F检验法(又称方差分析法)^[17]可以定量判断响应面模型的显著性。

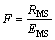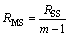，，     (2)

式中：R_SS为模型的总离差平方和；E_SS为残差平方和；m为因子数目；n为样本数目。给定显著水平α，F检验法则为：若F≥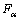(m-1, n-m)，则认为模型响应与因子间回归关系显著，否则认为回归关系不显著，可以逐次剔除最不显著的因子，重新进行试验设计。因子x_i的显著性可以用统计量S_i表示：

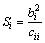                    (3)

其中：c_ii为矩阵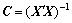主对角线的第i个元素，S_i越大说明x_i越显著。

(4) 构建优化函数。f_RSM代表响应面模型响应，与之对应的实测响应为f_exp。有限元模型修正可归结为以下优化问题：

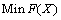
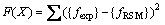
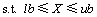            (4)

式中：lb和ub为设计空间范围。本文使用Matlab优化工具箱中的多目标优化函数fmincon。

2  改进的响应面方法

如何提高参数的修正精度是有限元模型修正技术研究的最终目标，基于响应面方法的结构模型参数修正中试验设计、响应面函数形式以及响应面函数拟合方法直接决定响应面函数模型的精度，是基于响应面方法结构模型参数修正的研究重点。

从几何观点来看，响应面法实际上是用一系列超曲面来代替实际的复杂函数关系。当某优化点周围一定数量的样本点的实际函数已知时，可通过试验设计获得样本点，利用方程回归方法建立一个曲面函数，在充分靠近这个优化点的区域内，可以用这个曲面函数来代替实际函数并进行复杂计算^[18]。

在刚度修正问题中，优化点就是真实刚度，样本点就是有限元模型中真实刚度周围一系列有代表性的值，样本点所在区域就是进行试验设计的设计空间。响应面模型能精确地代替有限元模型的重要条件是设计空间充分接近包含优化点的优化区域。

在此，利用单因素试验设计对响应面法中试验设计的设计空间进行优化。

2.1  基于单因素试验的设计空间优化法

首先假设桥梁的响应(m个测点挠度)与因子(k个梁段的抗弯刚度)之间满足一次关系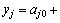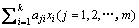。保持其他因子不变，使因子x₁在初始设计值的基础上产生改变量△x₁ (△x₁的符号可以视实测响应值与初始有限元模型计算值的大小关系确定) ，经有限元软件计算出y_j的变化量△y_j1，于是，y_j的表达式中x₁的系数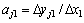；同理可知y_j的表达式中，x_i的系数。至此，可得到响应变化量与各因子改变量之间的线性函数为。以实测挠度相对于初始有限元模型计算值的变化量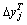作为目标函数值，构造优化函数：

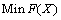
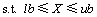             (5)

其优化解便是初始值的改变量，将改变后的初始值作为设计空间的中心点。这些中心点比初始值更接近优化点，因此，设计空间也更接近优化区域。

2.2  基于改进响应面的抗弯刚度识别

设计空间大小的取值遵循的准则为：使基于单因素试验的设计空间快速逼近优化区域，从而提高响应面模型修正的精度。在桥梁抗弯刚度识别中，单因素改变量可以取初始设计值的±50%，试验设计的边界为中心值±20%。

综上所述，利用静力测试基于改进响应面的抗弯刚度修正流程如图1所示。

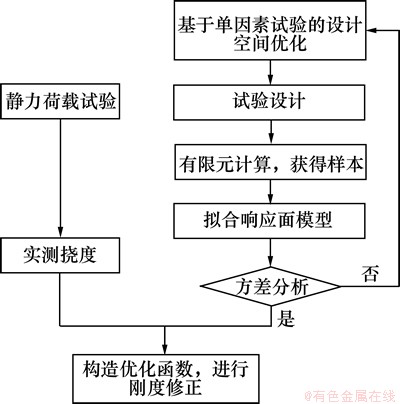
图1  基于改进响应面的抗弯刚度修正流程

Fig. 1  Flowchart of finite element model updating procedure based on improved RSM

3  数值算例分析

分别应用传统响应面法和本文提出的改进响应面法对1座(65+100+65) m三跨连续梁桥的有限元模型抗弯刚度进行修正。将2种方法的修正结果与假设的抗弯刚度对比，来验证改进响应面法的可行性。

在背景桥上指定13个挠度测试点，以相邻2个挠度测点之间的中点和支座位置为梁段节点将全桥分为13个梁段。响应为各测点挠度y_i，以13个梁段的抗弯刚度值M_i(i=1, 2, …, 13)为识别参数。梁段划分和挠度测试位置如图2所示。实际桥梁产生的损伤可能在全桥多个梁段同时发生，因此，假设上部结构边跨梁段②和刚度均减小15%，梁段⑥，⑦和⑧的刚度均减小20%，其余梁段①，③，④，⑤，⑨，⑩，_和刚度均减小10%。

3.1  优化设计空间

该数值算例是对旧桥进行抗弯刚度修正，因此令各抗弯刚度在设计值的基础上均降低50%，按2.1节所述方法构造挠度变化量与各梁段抗弯刚度改变量之间的线性函数：。按假定损伤情况计算全桥13测点理论挠度变化值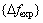，构造如式 (5)所示的优化函数，解得抗弯刚度改变向量△M，所以，13个梁段的抗弯刚度相对于初始设计值的系数如表1所示。以所得抗弯刚度值作为下一步试验设计的中心点。

表1  13梁段抗弯刚度初始值对设计值的系数

Table 1  Initial bending stiffness values of 13 segments

图2  三跨连续梁桥(65+100+65) m梁段划分与加载测试位置

Fig. 2  Substructure division and measuring positions of 3-span continuous beam bridge (65+100+65) m

3.2  建立一阶响应面模型

利用试验设计软件Minitab进行正交试验设计，经计算20次试验能代表并反映全面试验的效果，同时具有均衡分散、整齐可比的正交性。规定因子M_i设计边界为±20%M_i(M_i的值如表1所示)，由有限元软件进行数值计算可得20个样本点。由最小二乘法计算出系数矩阵，构造不含交叉项的一次响应面模型：y_i=f_i(M₁, M₂, …, M₁₃) (i=1, 2, …, 13)。试验因子数目m=13，样本点数目n=20，取显著水平α=0.05，则临界值F_0.05(12,7)=3.57，各回归方程的显著性F如图3所示。在各回归方程中，由式(3)计算自变量(即因子M_i，i=1, 2, …, 13)的显著性，剔除最不显著的自变量，用同样方法进行12因子正交试验设计，重新回归方程，并计算其显著性F。可以看到：各回归方程的显著性已经均满足要求，如图4所示。

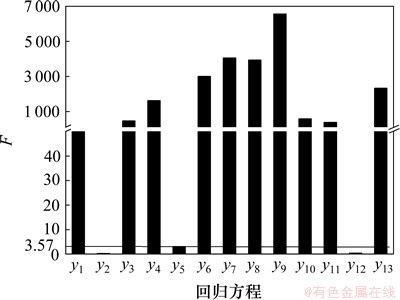
图3  参数筛选前方程F值

Fig. 3  F values before parameter screening

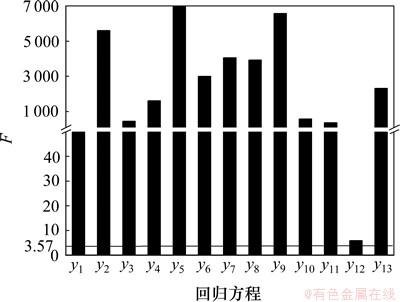
图4  参数筛选后方程F值

Fig. 4  F values after parameter screening

3.3  多目标刚度识别

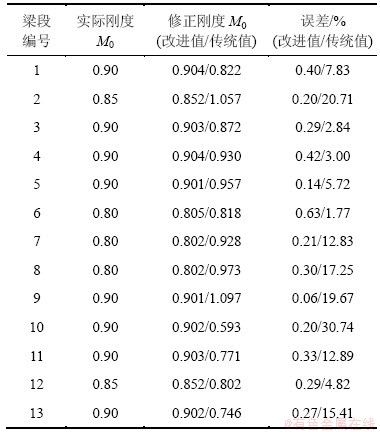
将各回归方程f_RSM和假定损伤情况下有限元模型计算值f_exp代入式(4)，将改进响应面法识别结果和传统响应面法识别结果见表2。

从表2可见：改进响应面法的修正结果误差均在1%以内，比传统响应面法有了很大改进。

表2  全桥梁段抗弯刚度识别结果

Table 2  Bending stiffness identification of all segments

4  实桥算例分析

4.1  工程概况

该桥为三跨连续梁桥，由南北引桥和主桥构成，全长231.16 m，主桥(40+65+40) m为变高度预应力连续箱梁。主桥采用桥梁博士建立平面杆系模型，共计148个单元，149个节点。在主桥上指定11 个挠度测试点，以相邻挠度测试点之间的中点和支座位置为梁段节点将全桥分为13个梁段。以各测点挠度y_i为响应，修正13个梁段的抗弯刚度M_j。挠度测试位置及梁段如图5所示。

2012-02对该桥进行了成桥静力荷载试验。加载车辆轴距为 1.4 m+4.0 m，总轴质量30 t，横向共布置3辆。加载时横桥向3辆车均匀分布，纵向以中间车轮加载到②号挠度测点为准，挠度实测值和初始有限元模型计算值比较如表3所示。

图5  挠度监测截面示意图(单位：cm)

Fig. 5  Schematic diagram of measuring positions

表3  挠度实测值和初始有限元模型计算值

Table 3  Comparison of measured deflection values and calculated values of FEM

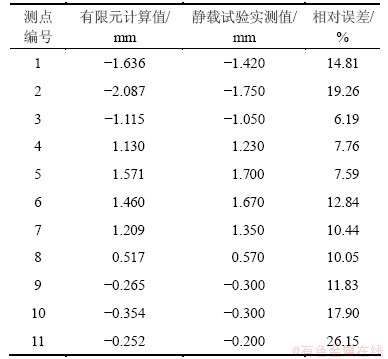
可见挠度实测值和初始有限元模型计算值相差较大，需进行抗弯刚度识别。

4.2  实桥抗弯刚度识别

4.2.1  设计空间优化

由表3可知：与初始有限元模型的挠度计算值相比，两边跨的测量值偏小，中跨测量值偏大。因此，在基于单因素试验的设计空间优化中，令边跨梁段的抗弯刚度在设计值的基础上增加50%，中跨梁段的抗弯刚度在设计值的基础上减小50%。按照2.1节所述方法可得13个梁段的抗弯刚度初始值相对于设计值的系数，如表4所示。

4.2.2  试验设计及样本矩阵

利用2水平正交设计方法进行11因子试验设计，经计算16次试验能代表并反映全面试验的效果，同时具有均衡分散、整齐可比的正交性。各个因子的中心值选取如表4所示，上下边界设定为中心±20%，用有限元软件计算出每次试验中的挠度，得到样本矩阵。

4.2.3  拟合响应面模型及方差分析

选择一次响应面函数形式，由最小二乘法求出待定系数。试验因子数目m=13，样本点数目n=16，取显著水平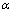=0.05，方差分析的临界值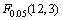= 8.74。各回归方程的显著性F均满足显著性要求。

4.2.4  构造优化函数进行损伤识别

将回归方程f_RSM和静载试验的挠度实测值f_exp代入式(4)，进行优化计算，将修正优化结果见表4。表4中第4列为基于本文方法的抗弯刚度修正结果，第3和第5列分别指单因素优化法优化的抗弯刚度值相对于初始值的变化范围以及在单因素优化基础上用响应面法修正的抗弯刚度相对于单因素优化值的变化范围。

表4  13梁段抗弯刚度修正值

Table 4  Updated bending stiffness values of 13 segments

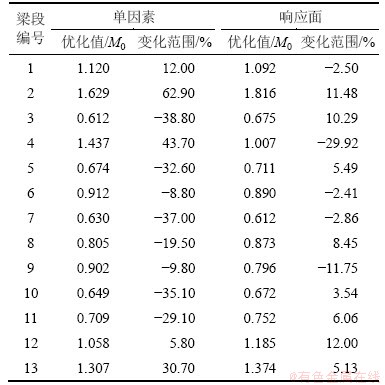
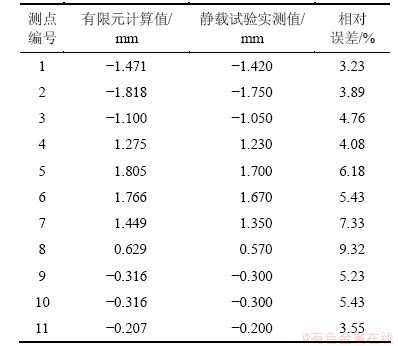
由改进响应面法修正的抗弯刚度代入有限元模型，计算出的挠度如表5所示。

计算结果表明：修正后的挠度较初始值有了很大的提高，能达到修正的效果，从参数的修正结果来看，抗弯刚度的变化和静载试验实测的挠度相吻合。由表5可以看出：单因素改变量基本在初始设计值±50%范围内，试验设计的边界基本在单因素优化值±20%范围内。

表5  挠度实测值和修正有限元模型计算值

Table 5  Comparison of measured deflection values and calculated value of updated FEM

本例结果表明：基于改进响应面的桥梁抗弯刚度识别取得了成功，对于设计空间的取值准则符合工程实际。该方法可推广至高阶模型，高阶响应面能模拟模型的曲面特性，得到更精确的修正结果，但在样本点个数一定的情况下要求试验设计空间更接近最优区域，因此，该方法的优越性将会在高阶响应面模型的应用中进一步体现出来。

5  结论

(1) 基于现代试验设计的响应面法是一个行之有效的快速有限元模型建模方法，在充分靠近优化点的区域内，可以有效地代替实际函数并进行复杂计算，在结构优化设计、模型修正与损伤识别等工程领域有很好的应用价值。

(2) 设计空间充分接近优化区域是提高响应面模型精度的一个非常重要的条件，本文提出了一种基于单因素试验法的改进响应面方法，实现了对设计空间的优化。数值算例的精确修正结果证明该方法具有很高的实际应用价值。利用改进响应面方法对三跨连续梁桥进行抗弯刚度修正，修正后的参数依旧保留了其真实的物理意义，抗弯刚度修正后计算挠度与实测挠度比较吻合，说明改进响应面法能使设计空间快速接近最优区域。

(3) 确定设计空间大小是响应面方法的一个重要内容。在桥梁抗弯刚度修正中，单因素改变量可以取初始设计值的±50%，试验设计的边界为优化中心值±20%。三跨连续梁实桥算例证明该取值范围是合适的。

参考文献：

[1] Yan Y J, Yam L H, Cheng L, et al. FEM modeling method of damage structures for structural damage detection[J]. Composite Structures, 2006, 72(2): 193-199.

[2] Cornwell P, Doebling S W, Farrar C R. Application of the strain energy damage detection method to plate-like structures[J]. Journal of Sound and Vibration, 1999, 224(2): 359-374.

[3] Mohamed A A. Parametric study of using only static response in structural damage detection[J]. Engineering Structures, 2012, 34(2): 124-131.

[4] 石雪飞, 杨琪, 阮欣. 已建大跨径PC梁桥过量下挠及开裂处治技术[M]. 北京: 人民交通出版社, 2010: 51-58.

SHI Xuefei, YANG Qi, RUAN Xin. The treatment technology of big deflection and cracks in existing large span prestressed concrete beam bridges[M]. Beijing: China Communications Press, 2010: 51-58.

[5] Yan Y J, Hao H N, Yam L H. Vibration based construction and extraction of structural damage feature index[J]. International Journal of Solids and Structures, 2004, 41(24/25): 6661-6676.

[6] FANG Shengen, REN Weixin, Perera R. A stochastic model updating method for parameter variability quantification based on response surface models and Monte Carlo simulation[J]. Mechanical Systems and Signal Processing, 2012, 33(1): 83-96.

[7] REN Weixin, CHEN Huabing. Finite element model updating in structural dynamics by using the response surface method[J]. Engineering Structures, 2010, 32(2): 2455-2465.

[8] 邓苗毅, 任伟新. 基于响应面方法的结构有限元模型修正研究进展[J]. 铁道科学与工程学报, 2008, 5(3): 42-44.

DENG Miaoyi, REN Weixin. Study on structure finite element model updating based on response surface methodology[J]. Journal of Railway Science and Engineering, 2008, 5(3): 42-44.

[9] 郭勤涛, 张令弥, 费庆国. 用于确定性计算仿真的响应面法及其试验设计研究[J]. 航空学报, 2005, 26(1): 55-60.

GUO Qintao, ZHANG Lingmi, FEI Qingguo. Response surface method and its experimental design for deterministic computer simulation[J]. Acta Aero-Nautica Et Astronautica Sinica, 2005, 26(1): 55-60.

[10] FANG Shengen, Perera R. Damage identification by response surface based on model updating[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 717-733.

[11] Doebling S W, Farrar C R, Prime M B. A summary review of vibration-based damage identification methods[J]. The Shock and Vibration Digest, 1998, 30(2): 91-105.

[12] Yan Y J, Cheng L, Wu Z Y, et al. Development in vibration- based structural damage detection technique[J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2198-2211.

[13] Montgomery D C. 实验设计与分析[M]. 汪仁官, 陈荣昭, 译.北京: 中国统计出版社, 1998: 563-575.

Montgomery D C. Design and analysis of experiments[M]. WANG Renguan, CHEN Rongzhao, transl. Beijing: Chinese Press of Statistics, 1998: 563-575.

[14] 何为, 薛卫东, 唐斌. 优化试验设计方法及数据分析[M]. 北京: 化学工业出版社, 2012: 1-6.

HE Wei, XUE Weidong, TANG Bin. Optimization of experimental design method and data analysis[M]. Beijing: Chemical Industry Press, 2012: 1-6.

[15] 方圣恩. 基于响应面模型修正的结构损伤识别[C]// 第10届全国振动理论及应用学术会议论文集. 南京, 2011: 747-748.

FANG Shengen. Structural damage identification based on response surface model updating[C]// 10th National Vibration Technology and Application. Nanjing, 2011: 747-748.

[16] Jones D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21: 345-383.

[17] 王岩, 隋思莲. 试验设计与MATLAB数据分析[M]. 北京: 清华大学出版社, 2012: 81-82.

WANG Yan, SUI Silian. Experimental design and MATLAB data analysis[M]. Beijing: Tsinghua University Press, 2012: 81-82.

[18] 韩芳, 钟冬望, 磨季云. 基于改进响应面法的结构模型修正研究[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(1): 196-197.

HAN Fang, ZHONG Dongwang, MO Jiyun. Research on model updating based on improved response surface method[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2012, 36(1): 196-197.

(编辑  何运斌)

收稿日期：2013-06-29；修回日期：2013-08-07

基金项目：广东省交通运输厅科技项目(科技-2012-02-028)

通信作者：石雪飞(1964-)，男，江苏泰州人，教授，博士生导师，从事桥梁施工信息与技术研究；电话：13701803862；E-mail: shixuefei@gmaill.com