文章编号:1004-0609(2008)03-0511-05
粉末注射成形充模流动过程模壁凝固层增长的计算与模拟
郑洲顺1,曲选辉2,韩旭里1,张国栋3
(1. 中南大学 数学科学与计算技术学院,长沙 410083;
2. 北京科技大学 材料科学与工程学院,北京 100083;
3. 中南大学 粉末冶金国家重点实验室,长沙 410083)
摘 要:应用微流边界层理论从微观上阐述了粉末注射成形充模过程模壁凝固层的存在性,分析了PIM模壁凝固层的结构,它包含微流边界层,其厚度远远小于L.Prandtl边界层的厚度,说明假设在PIM充模流动过程中无滑移边界条件是合理的。根据L.Prandtl边界层厚度的计算方法和微流边界层的定义,建立了计算PIM浇道模壁凝固层厚度的数学模型,数值模拟结果说明所给数学模型较好地描述浇道模壁凝固层的增长情况。利用该模型可以方便地预测浇道模壁凝固层厚度的增长,为优化影响制品质量的工艺参数提供了理论依据。
关键词:粉末注射成形;微流边界层;模壁凝固层;数值模拟
中图分类号:TF 12 文献标识码:A
Computation and simulation of solidification on wall of
cavity in powder injection molding filling process
ZHENG Zhou-shun1, QU Xuan-hui2, HAN Xu-li1, ZHANG Guo-dong3
(1. School of Mathematical Science and Computing Technology, Central South University, Changsha 410083, China;
2. School of Materials Science and Engineering, University of Science and Technology Beijing, Beijing 100083, China;
3. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)
Abstract: The existence of solidification layer on the wall of cavity in powder injection molding filling process by boundary layer theory of microflow was reviewed. The structure of solidification layer on the wall of cavity was analyzed. Based on the computation method of L.Prandtl boundary layer and the definition of boundary layer of microflow, the mathematical model of solidification layer on the wall of cavity in powder injection molding filling process was established. The results of the numerical simulation indicate that the thickness of the solidification layer on the wall of feed channel can be nicely described by the mathematical model. Some useful information for predicting and controlling the solidification on the wall of cavity can be supplied by the mathematical model established.
Key words: powder injection molding; boundary layer of microflow; solidification layer on wall of cavity; numerical simulation
粉末注射成形(Powder injection molding,PIM)是一种源于传统塑料注射成形的新型粉末冶金近净形成形技术,由于其在制作几何形状复杂、组织结构均匀及高性能的近净形产品方面具有独特的技术和经济优势而倍受瞩目[1-3]。在PIM过程中,喂料熔体接触到冷模壁时,在熔体和模壁接触界面形成冷凝层,冷凝层不断向内部扩展,使得熔体流动通道截面不断减小甚至闭合,从而增加了熔体的流动阻力,造成充填困难。同时,随着凝固层的不断扩展,熔体截面上的压力和温度梯度将导致不均匀的热应力和分子取向,影响制品的均质性。解决的方法是降低喂料熔体的粘度,增加注射压力和注射速度或提高模温。随着产品性能要求的提高,注射成型制品逐渐采用具有高熔融温度和高粘度的高性能喂料熔体,从而过于依赖高的注射速度和注射压力会导致产品生产的能耗增加,降低其经济性,也会限制成型工艺参数的优化。本文作者将微流边界层理论[4]应用于PIM充模流动过程模壁凝固层形成的研究,建立了描述PIM浇道模壁凝固层厚度增长的数学模型,为分析和预测模壁凝固层的增长变化提供了理论依据。
1 PIM过程的微流边界层
1.1 表面能与微流边界层
微流边界层理论以物质结构理论为基础,研究固体表面分子对液体分子的吸附、固壁对液体的引力作用,分析边界层内液体的粘度系数表达式,推导边界层内液体流动微分方程。在微流边界层中,固体表面的宏观结构主要是指固壁的突出不平度、表面波纹度和表面粗糙度。处于固体表面的分子、原子或离子的吸引力和表面键能的特性,取决于固体内部结构及表面的结构特点。对于粉末注射成形工艺的模具,其表面往往采用机械加工方式形成,这种表面对外显示的不饱和键往往具有金属键的性质。固体表面对液体的吸附能力,一方面决定于液体分子的特性,另一方面决定于固体表面的自由能,也就是固体表面键能,因此,可以用固体表面未饱和键能来衡量其对液体分子的吸附能力。对于具有金属键的固体,类似于共价键晶格的固体,断裂面是金属键或原子键,这类表面具有较强的偶极作用,对液体分子的吸引力强。因此,在分析PIM充模流动过程是否满足无滑移边界条件和模壁凝固层的增长情况时,应考虑模具固壁表面的特性和喂料熔体分子特性。把微流边界层理论应用于PIM充模流动过程的研究,分析了边界层的速度分布规律和粉末颗粒在喂料熔体中的沉降速度等,有助于分析研究PIM模壁凝固层的增长和成形坯中粉末颗粒的分布情况。
1.2 静液边界层与L.Prandtl边界层
固体表面与液体分子间的相互作用,使得靠近固体表面的液体层具有不同的性质,称这一液体层为 静液边界层。静液边界层的结构决定于固体表面性质,而表面的极性又是影响该静液边界层结构的重要因素。静液边界层中,紧贴于固壁的一层液体分子,由于受到固壁强烈的吸引作用,看似液态,实际上具有固体的性质,而离开固壁的第二、三层液体分子层,同样受到固壁分子的引力,具有一定弹性,虽然是液态,却具有半固态的性质。静液边界层是由于固体表面对液体分子的吸引作用而形成的,因此,该边界层的厚度应该是固体表面对外界液体分子作用的整个区域。一旦固体表面的性质确定后,固体表面分子对液体分子的吸引力可表示为[4]:

由此可见,固体表面分子对液体分子的吸引力随着离开固体表面的距离增加而迅速减小,与距离的六次方成反比。分子间的有效距离一般为0.3~0.5 nm,如果以这样的数值考虑,对于水固体表面的静水边界层的厚度只有0.3~0.5 nm,也就是2至3个水分子层。实际上,分子间力不具有饱和性,但具有叠加性,固体表面的一个分子对水分子的作用范围为0.3~ 0.5 nm,但是固体表面具有非常多的分子,一个水分子受到的引力是无数固体表面分子起作用的总和。也就是说,固体表面众多分子的作用,对外界物质分子形成了一种引力场,该引力场的作用范围远远大于一个分子的引力范围,进入该引力势场中的物质分子均将受到其引力作用。固体表面对液体分子的引力势能表达式为

当固体表面一定,温度不变时,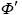 可看成常数,n是指数;对于两个分子,n=6;对于固体表面,0< n<6;在一般情况下,n为2~3。
可看成常数,n是指数;对于两个分子,n=6;对于固体表面,0< n<6;在一般情况下,n为2~3。
由于分子引力的作用,流体始终要粘附于固壁上,这就意味着摩擦力阻滞了固壁附近薄层内流体的运动。在这个薄层内,流体的速度从固壁处的零(无滑移)逐渐增加到相应的无摩擦外流原有值。这个薄层称为L.Prandtl边界层。显然,L.Prandtl边界层是由于粘性的存在引起的,粘性越大,边界层厚度越大。若流体没有粘性(理想流体),则L.Prandtl边界层不存在。但静液边界层却始终存在,只是相当薄而已。从这一意义来说,无滑移边界条件的假设在PIM充模流动过程中总是得到满足的,因此,PIM模壁凝固层也总是存在的,只是厚度是否可以忽略而已。
2 PIM充模过程模壁凝固层与L.Prandtl边界层的关系
2.1 PIM模壁凝固层的结构
由微流边界层和L.Prandtl边界层厚度的定义可知,对于粉末注射成形充模流动过程,L.Prandtl边界层的厚度并不是就是PIM模壁凝固层的厚度。通常意义下,PIM模壁凝固层的厚度定义为模具壁面到熔体速度为零处的距离。实际上,除了模壁边界上受固体壁面分子引力场吸引的很薄的一层熔体外,靠近模壁的熔体速度都不可能为零。因此,PIM模壁凝固层的厚度应定义为熔体速度接近零处到壁面的距离,或速度与注射速度相差很大处到壁面的距离。由此可见,PIM模壁凝固层的厚度远远小于L.Prandtl边界层的厚度,它包含微流边界层的厚度,其关系示意图如图1所示。PIM模壁凝固层的厚度等于微流边界层的厚度加上 L. Prandtl边界层中速度接近零部分的厚度。这里的微流边界层是指受固体壁面分子引力场吸引而速度为零的流体薄层,其厚度可以根据具体的材料体系由式(2)来计算,对于具体PIM过程,可假设其厚度为常数h0。
PIM模壁凝固层的形成,既有微流边界层形成的原因,也有L.Prandtl边界层形成的原因。由于分子间的有效距离一般为0.3~0.5 nm,因此,PIM模壁凝固层的厚度至少是微流边界层的最小厚度0.3 nm。由于微流边界层的厚度较小,因此,本研究以L.Prandtl边界层厚度的变化来估算PIM模壁凝固层厚度的增长变化情况。PIM喂料熔体是非牛顿流体,在PIM充模流动过程中,从边界到流体中心喂料熔体的粘度有明显的梯度。
2.2 PIM过程中L.Prandtl边界层厚度计算公式的推导
在边界层外,粘性相对较小,而在边界层内,惯性力与摩擦力处于相当的数量级。流体单位体积的惯性力为 ,对于长度为l的平板,梯度
,对于长度为l的平板,梯度 正比于v/l,其中v表示L.Prandtl边界层外缘的流体速度,故惯性力具有
正比于v/l,其中v表示L.Prandtl边界层外缘的流体速度,故惯性力具有 的数量级。单位体积的摩擦力等于
的数量级。单位体积的摩擦力等于 ,在层流流态下,
,在层流流态下, 。设L.Prandtl边界层的厚度为δ,则速度梯度
。设L.Prandtl边界层的厚度为δ,则速度梯度 的量级为v/δ,因此,单位体积的摩擦力为
的量级为v/δ,因此,单位体积的摩擦力为 =
=  。由于L.Prandtl边界层内摩擦力与惯性力相当,故有下式[3]:
。由于L.Prandtl边界层内摩擦力与惯性力相当,故有下式[3]:

从而可知L.Prandtl边界层厚度δ为

由式(3)可知,液体的运动粘度越大,L.Prandtl边界层的厚度越大,平板的长度越长,L.Prandtl边界层的厚度越大。由此可见,对于粉末注射成形加大注射速度可降低L.Prandtl边界层的厚度。若用流体的综合指标Re1表示,则边界层的无量纲厚度(相对厚度)与Re1成反比,即Reynolds数增加,L.Prandtl边界层相对厚度减小。在无摩擦流动的极限情况下,Re1→∞时,L.Prandtl边界层的厚度为零。L.Prandtl边界层厚度的定义在一定程度上是任意的,由于从固体表面上流体速度为零开始,离开表面的速度增加,直至离开无穷远处,速度才等于来流速度。从理论上讲,L.Prandtl边界层厚度是无限大的。但实际上,离开固体表面不远的地方,流体的速度已经非常接近来流速度,因此,可以把边界层厚度定义为速度与外部速度相差为1%处到壁面的距离,这里的壁面实际指速度为零处。用这个定义,就可以得到式(3)[3]中的比例系数k为5。
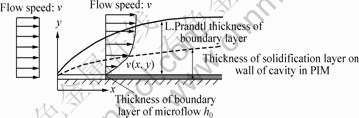
图1 PIM模壁凝固层厚度与L.Prandtl边界层厚度的关系
Fig.1 Relationship between thickness of solidification layer on wall of cavity in PIM and L.Prandtl thickness of boundary layer
3 PIM充模过程模壁凝固层增长的计算公式
根据PIM模壁凝固层厚度的定义(见图1),PIM模壁凝固层的厚度等于微流边界层的厚度加上L.Prandtl边界层中速度接近零的部分的厚度。因此,对于平板面,PIM模壁凝固层的厚度h(x)可以由微流边界层的厚度h0和式(3)来计算,即
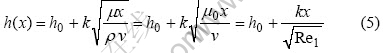
这里将热传导等引起的凝固层厚度变化都归结于喂料熔体粘度μ的变化中。在实际应用中,一般把粉末注射成形混合喂料的粘度方程简化成[5-8]:

若也把L.Prandtl边界层厚度定义为速度与外部速度相差为1%处到壁面的距离,这里的壁面实际指速度为零处,则同样可以得到式(5)中的比例系数k为5。式(5)给出了PIM简单型腔模壁凝固层厚度h(x)的计算方法。复杂型腔PIM模壁凝固层厚度h(x)的增长变化情况比较复杂。在研究和实际生产中,需要了解的主要是浇道模壁和某些关键点处凝固层厚度增长的变化情况,判断是否由于凝固层厚度增长而导致发生欠注等缺陷。浇道模壁凝固层厚度增长的变化情况可以用式(5)来计算,对某些关键点处凝固层厚度增长变化的情况可以将式(5)中的x转换为相应的充填时间t后进行计算。
4 PIM充模过程模壁凝固层增长的数值模拟
用式(5)来计算PIM模壁凝固层厚度的关键是粘度μ的估算,只要能计算粘度μ的取值范围,就能用式(5)对PIM模壁凝固层厚度进行预测和控制,以免造成充填困难,影响制品的质量。通过对PIM充模流动过程进行数值模拟[9-14],可求出模腔内任意位置任意时刻喂料粘度μ的近似值及其分布情况。图2所示 为以有限元分析软件ANSYS对PIM充模时间为 0.471 112 s时浇道与模腔内粘度分布的数值模拟结果,图3所示为其相应的速度分布的数值模拟结果[15]。
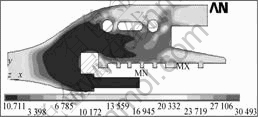
图2 PIM充模过程粘度分布的数值模拟
Fig.2 Numerical simulation of viscosity distribution at t=0.471 112 s of filling stage

图3 PIM充模过程速度分布的数值模拟
Fig.3 Numerical simulation of velocity distribution at t= 0.471 112 s of filling stage
从图2可以看出,浇道模壁有一层很薄的凝固层,其厚度从浇口逐渐增加,速度接近零的范围比此层厚度大;模内边界上的凝固层变化类似,但复杂得多,这与式(5)描述的结果较相符。因此,利用数值模拟得出的浇道内任意时刻任何位置的μ,再根据注射速度便可由式(5)计算出PIM浇道模壁凝固层厚度h(x)。相关的数值模拟和计算结果[16-18]也表明,一般的PIM浇道模壁凝固层厚度很小,且充模过程是在短时完成,只要喂料熔体的粘度适中,浇道模壁凝固层的增长不会造成熔体流动通道闭合,使得充填困难。但对于微PIM过程,模壁凝固层厚度的计算和控制则非常重要。
5 结论
1) 将微流边界层理论应用于PIM充模流动过程的研究,应用微流边界层理从微观上阐述了PIM充模过程模壁凝固层的存在性,说明在PIM充模流动过程中假设无滑移边界条件是合理的。
2) 根据L.Prandtl边界层厚度的计算方法和微流边界层的定义,分析了PIM模壁凝固层的结构,给出了PIM浇道模壁凝固层厚度的计算公式。
3) 数值模拟和计算结果表明所给计算公式较好地描述浇道模壁凝固层增长的情况;对微PIM过程,浇道模壁凝固层厚度的计算和控制则非常重要,所给计算公式为微PIM过程工艺参数的优化提供了更科学的依据。
REFERENCES
[1] ZHENG Zhou-shun, QU Xuan-hui, AO Hui. Computer numerical simulation of powder injection molding process[J]. China Mechanical Engineering, 2002, 13(14): 1257-1260.
[2] GERMAN R M, HUANG K X. The condition of MIM, PIM and relative PM technology in the USA[J]. Powder Metallurgy Technology, 2006, 24(5): 384-387.
[3] ROSOF B H. The metal injection molding process comes of age[J]. J of Mater, 1989, 41(8): 13-16.
[4] 文书明. 微流边界层理论及其应用[M]. 北京: 冶金工业出版社, 2002.
WEN Shu-ming. Microflow boundary layer theory and applications[M]. Beijing: Metallurgical Industry Press, 2002.
[5] ZHENG Z S, QU X H. Numerical simulation of powder injection moulding filling process for intricate parts[J]. Powder Metallurgy, 2006, 49(2): 167-172.
[6] LAM Y C, CHEN X, TAM K C, YU S C M. Shear-induced particle migration modeling in a concentrated suspension flow[J]. Modelling and Simulation in Materials Science and Engineering, 2003, 11(4): 503-522.
[7] LI Y M, LIU X Q, LUO F H, YUE J L. Effects of surfactant on properties of MIM feedstock[J]. Transactions of Nonferrous Metals Society of China, 2007, 17(1): 1-8.
[8] ZHU B J, QU X H, TAO Y. Mathematical model for condensed-solvent debinding process of PIM[J]. Journal of Materials Processing Technology, 2003, 142: 487-492.
[9] QU X H. Numerical simulation of feedstock melt filling in a cylindrical cavity with solidification in powder injection molding[J]. Trans of NMSC, 1998, 8(4): 544-549.
[10] KWON T H. Numerical simulation of powder injection molding filling process for three-dimensional complicated cavity geometries[J]. Advances in Powder Metallurgy and Partiallar Materials, 1996, 15: 19-79.
[11] HWANG C J, KWON T H.A full 3D finite element analysis of powder injection moldingfilling process including slip phenomena[J]. Polymer Engineering and Science, 2002, 42(1): 33-50.
[12] HWANG C J, KWON T H.Finite element analysis of PIM filling process with slipcharacterization of powder-binder mixtures[J]. Journal of the Japan Society of Powder and PowderMetallurgy, 1999, 46(8): 837-843.
[13] LIN F, ZHENG Z S, QU X H. Numerical simulation of PIM filling process based on second development of ANSYS[J]. Computer Engineering and Applications, 2005, 41(3): 194-197.
[14] BICKERTON S, ABDULLAH M Z. Modeling and evaluation of the filling stage of injection/compression moulding[J]. Composites Science and Technology, 2003, 63(10): 1359-1375.
[15] 郑洲顺, 曲选辉, 雷长明. PIM充模流动过程喂料粘度的变化与缺陷形成[J]. 金属学报, 2007, 43(2): 187-193.
ZHENG Zhou-shun, QU Xuan-hui, LEI Chang-ming. Defects and variation of viscosity in powder injection molding filling process[J]. Acta Metallurgica Sinica, 2007, 43(2): 187-193.
[16] GUO S B, QU X H, XIANG J H, ZHANG R.F, HE X M, LI M S, DUO S W, LI W K. Effect of annealing processing on microstructure and properties of Ti-6Al-4V alloy by powder injection molding[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(S2): 701-704.
[17] GUO J F, XIANG H, ZHENG Z S. Computer simulation of die filling process for a MIM part[J]. Powder Metallurgy Technology, 2005, 123(1): 26-31.
[18] ZHENG Zhou-shun, QU Xuan-hui. The fundamental equation of two-dimensional layer flows of the melt feedstock in the powder injection molding process[J]. Chinese Journal of Engineering Mathematics, 2005, 22(2): 268-272.
基金项目:国家重点基础研究发展计划资助项目(2006CB605207);湖南省科技计划博士后专项基金资助项目(2007RS028);中南大学博士后基金 资助项目
收稿日期:2007-06-14;修订日期:2007-10-11
通讯作者:郑洲顺,教授,博士;电话:0731-8660172;E-mail: zszheng@mail.csu.edu.cn
(编辑 李艳红)