针对初值敏感性的高阶FastICA改进算法

季策¹，胡祥楠¹，朱丽春²

 (1. 东北大学 信息科学与工程学院，辽宁 沈阳，110004；

2. 中国科学院 国家天文台，北京，100012)

摘要：在三阶收敛的FastICA算法基础上，针对其对初始值的选择比较敏感，容易影响收敛效果的问题，通过引入最速下降法对随机产生的初值进行处理。结果表明：改进后的算法不依赖于初始值的选择，克服了初值敏感性的问题，进而提高了算法的收敛性能。

关键词：独立分量分析；牛顿迭代法； FastICA； 最速下降法；初值敏感性

中图分类号：TN 911.6          文献标志码：A         文章编号：1672-7207(2011)S1-0672-05

Improved higher order FastICA algorithm based on initial value sensitivity

JI Ce¹, HU Xiang-nan¹, ZHU Li-chun²

(1. School of Information Science and Engineering, Northeast University, Shenyang 110004, China;

2. National Astronomical Observatories, Beijing 100012, China)

Abstract: The steepest descent method was applied to process the randomly generated initial value on the basis of the third order convergence Newton iteration method which is sensitive to the choice of initial value and easily affects the convergence effect. The results show that the improved algorithm does not depend on the choice of the initial value and overcomes the sensitivity of initial value, thus enhances the capability of convergence of algorithm.

Key words: independent component analysis; Newton iteration method; FastICA; steepest descent method; initial value sensitivity

独立分量分析方法(Independent component analysis，ICA)是近年发展起来的一种有效的盲信号分离方法^[1]。该技术是在不知接收信号瞬时混叠参数的情况下，仅仅根据输入源信号的一些基本统计特征，由观测信号恢复出源信号。

ICA 的简单形式为：设一组信号X={x₁，x₂，…，x_m}是另一组源信号S={s₁，s₂，…，s_n}的观测值。假设第i个观测信号x_i由n个独立分量s线性混合而成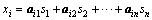：，i=1，2，…，m，即

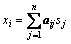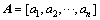。其中：称为混合矩阵,

a_j称为混合矩阵的基向量。ICA的目的就是要寻找一个矩阵W，使得y=Wx， 要求输出信号y_i相互独立, 则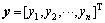就是s的估计值。目前，该技术已广泛应用于语音处理、生物医学工程及图像处理等领域^[2]。

FastICA具有收敛速度快的优点，特别是改进的FastICA算法，具有三阶的收敛速度^[3]，虽然改进的高阶算法具有较快的收敛速度，但仍存在对初始权值要求较高的问题，若初始矩阵为随机矩阵，不同的运算，收敛次数相差较大，无法保证得到均匀的收敛速度。本文作者在三阶收敛的FastICA算法的基础上，通过对初始值进行有效地处理，达到改善算法的收敛性能和初值敏感性的目的，进而提高了盲信号分离的效率。

1  FastICA算法原理

1.1  FastICA算法

FastICA 算法,即固定点(Fixed-point)算法,是芬兰赫尔辛基工业大学计算机及信息科学实验室Hyvarinen^[4]提出并发展起来的。

FastICA的学习规则是要寻找一个方向，使w^Tx具有最大的非高斯性。基于负熵FastICA算法的目标函数为^[5]：

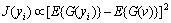        (1)

其中：G是一任意非二次型函数；y_i是具有零均值和单位方差的随机变量；v是具有零均值和单位方差的高斯随机变量。将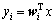代入上式得：

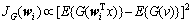     (2)

由此可见：若使负熵J_G(w_i)达到极大，即在||w_i||=1的约束条件下，使得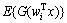达到极大，用拉格朗日乘子方法可以得到固定点算法的目标函数为^[6]：

         (3)

对式(3)求权值w_i的一次梯度得：

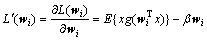     (4)

其中：g为G的导数，对式(4)再次求权值w_i的梯度为：

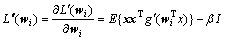   (5)

其中：g′为g的导数，因为

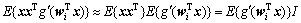(6)

由牛顿迭代法求出方程L′(w_i)=0的近似根为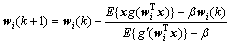^[7]：

    (7)

由于L′(w_i)=0，并考虑权向量归一化条件：||w_i||=1，有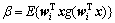，代入式(7)，且两边同乘以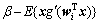，可得一元定点算法的迭代公式为：

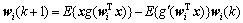    (8)

其中：k为迭代次数，在每次迭代后需要对权向量w_i(k+1)进行归一化处理：

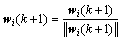          (9)

上述公式需要对源信号进行白化处理，如果是处理未经白化的数据，可用下面的迭代公式和权值归一化求解^[6]：

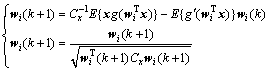 (10)

其中：C_x=E{xx^T}是观测信号的协方差矩阵。

1.2  三阶收敛的“类牛顿”迭代法

传统的牛顿迭代法具有二阶的收敛速度，高阶收敛的牛顿迭代法，是在式(1)的基础上，通过分析变换，使其具有三阶或更高阶的收敛速度。

牛顿迭代法^[8]如下：

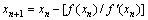         (11)

式(11)具有二阶收敛速度。对牛顿迭代算法进行修正^[9]得到：

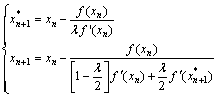   (12)

其中：n=0，1，2，…。当非零参数λ取任意不同的值时，迭代均收敛，因此，将该公式称为“类牛顿”迭代公式。由文献[9]可知，修正后的牛顿迭代算法至少具有三阶的收敛速度，通过适当调整λ的值(取λ=1)，使得“类牛顿”迭代方法产生的序列具有更高的精确度。

根据式(12)，文献[3]给出了三阶收敛的FastICA算法：

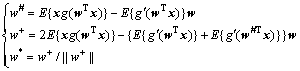(13)

2  改进的高阶FastICA算法

在FastICA算法中，采用牛顿迭代算法估计w的值，其优点是收敛快、形式简单；其缺点是对初值要求较高，由于FastICA算法的初始权值一般是随机选取的，因此，就会因为初始权值的不同而导致每次迭代效率不同，得到的独立分量也会稍有不同，特别是对源信号独立性不太好的情况，对权值的选取比较敏感，不同的初始权值可能导致收敛性能的不同，甚至会出现收敛和不收敛的两种极端的情况。虽然可以选取白化过程中获得的主成分作为初始权值，但算法很容易收敛到该白化初始值。为了较好地解决该问题，既要放宽算法对初始权值的要求，又不能影响算法的收敛速度。从这个角度出发，需要找到一种方法与牛顿迭代法联用，先用该方法求得较好的近似值，再利用牛顿迭代法继续求出最优解。理论分析表明：最速下降法能够满足这种要求，最速下降法具有对初值不敏感的特点^[10](收敛速度较慢)。因此，可利用最速下降法先求出近似值，再结合高阶收敛的FastICA算法求出最优解。仿真实验表明这是一种较好的组合方法。

2.1  最速下降法

最速下降法是以负梯度方向作为下降方向的优化算法，又称梯度法，是1874年法国科学家Cauchy提出的，最速下降法是无约束优化算法中最简单的    方法^[11]。

最速下降法的计算步骤为：

(1) 选取一初始化随机正交阵W=[w₁，w₂，…，w_n]，令k=0 ；

(2) 计算E{xg(w^Tx)}在W处的梯度值；

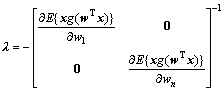  (14)

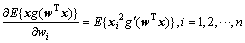其中：。由

多元微分学可知，负梯度的方向就是函数值下降最快的方向。因此，将梯度值作为松弛因子，代入式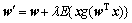；检验是否收敛，若收敛，取w₀=w′，若不收敛，取k=k+1，转步骤(2)。

2.2  改进的三阶收敛牛顿迭代算法的具体步骤

(1) 将观测信号x进行中心化处理；

(2) 对中心化后的x进行白化处理；

(3) 初始化随机权矢量w，利用最速下降法求出w₀，设置收敛误差ε=1×10^-6；

(4) 按式(13)式调整w_k+1，计算w_k+1后，用式(9)进行相关和归一化；

(5) 如果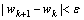，则算法收敛，估算出一个独立分量，否则重复步骤(4)和(5)；

(6) 由分离矩阵W，得到源信号的所有估计y_i，输出估计信号Y。

牛顿迭代算法和最速下降法作为常用的优化算法，各有优缺点。在改进的算法中，将两者结合使用，扬长避短。首先，利用最速下降法对初值不敏感且迭代初期下降较快的特性，求出合适的初值。算法中由于不需要求出精确的近似解，为减少计算量，只使用梯度作为下降方向，没有再进行一维搜索求下降的量。然后，利用改进牛顿迭代法在收敛点附近的三阶收敛速度，使用最速下降法提供的初值，求出最后的收敛结果。

3  仿真实验和算法分析

3.1  仿真实验

首先，对两幅原始图像(图 1) 按随机生成的2×2矩阵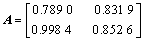混合, 得到一组混合图

像(图 2)；然后，分别用基本FastICA和改进的FastICA算法对图像进行处理,得到分离后的结果，如图3和4所示。可以看出,改进算法可以成功分离混合信号。

图1  原始图像

Fig.1  Original images

图2  混合后图像

Fig.2  Mixed images

图3  原始FastICA分离后的图像

Fig.3  Separated images of original FastICA

图4  改进的三阶收敛FastICA算法分离后的图像

Fig.4  Separated images of improved third-order convergence FastICA algorithm

3.2  算法的性能分析

通过ICA的求解得到混合矩阵和源信号的估计值，与混合矩阵和源信号的实际值进行比较，就可以评价ICA算法的性能。

通过式(15)来衡量算法的分离性能^[12]：

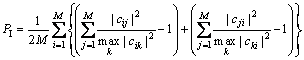(15)

其中：C=WA=c_ij；M为变量数。P_I表示算法的分离性能，其值越小，表示分离的性能越好，当P_I=0时表示信号完全分离。计算可得各算法的P_I见表1(FastICA-T为三阶收敛牛顿迭代法)：

表1  不同算法的PI比较

Table 1  Comparison of P_I by different calculating methods

由表1可以看出：改进后的算法与原算法的性能指标几乎相同,说明改进的算法也较好地保留了原图像的信息。

对FastICA 和改进算法的收敛速度进行比较，每种算法均随机进行了8次分离运算，记录每种算法的迭代次数和平均迭代次数，结果见表2。

表2  迭代次数的比较

Table 2  Comparison of iteration steps

从表2可以看出：使用原始FastICA算法的收敛速度不均匀，波动较大；采用改进的快速算法时，首先使用最速下降法 1~3步,求出分离矩阵值w₀，然后进行迭代，迭代次数较少，收敛速度较快，且收敛速度均衡。改进的算法较好地解决了初值敏感性的问题，但是，使用最速下降法消耗了一定的时间。仿真结果表明：改进的快速算法能明显加快收敛速度，避免收敛速度不均匀的问题。

4  结论

针对牛顿迭代法对初值敏感的问题，在三阶收敛牛顿迭代算法的基础上，应用最速下降法给出了一种改进形式的高阶FastICA算法。实验表明，改进后的算法在保持收敛速度的情况下，能避免收敛速度不均衡的问题，实现了大范围的收敛。

参考文献：

[1] Castano S, Ferrara A, Montanelli S, et al . H ELIOS: A general framework for ontology-based know ledge sharing and a evolution in P2P systems[C]//The 14th International Workshop on Database and Expert Systems Applications. Prague: IEEE Press, 2003: 597-603.

[2] 张启发, 张斌, 张希斌. 盲信号处理及应用[M]. 西安: 西安电子科技大学出版社, 2006.
ZHANG Qi-fa, ZHANG Bin, ZHANG Xi-bin. Operation and application of blind signal[M]. Xi’an: Xidian University Press, 2006.

[3] JI Ce, YU Yang, YU Peng. A new FastICA algorithm of Newton’ iteration[C]//Proceedings of ICETC 2010. 2010: 481-484.

[4] Hyv?rinen A. Independent component analysis: Algorithms and applications[J]. Neural Networks, 2000, 13: 411-430.

[5] Cui H, Wen J R, Nie J Y, et al . Query expansion by mining user logs[J]. IEEE Transactions on Knowledge and Data Engineering, 2003, 15(4): 1-11.

[6] 斯华龄, 张立明. 智能视觉图像处理—多通道图像的无监督学习方法及其他方法[M]. 上海: 上海科技教育出版社, 2002.
SI Hua-ling, ZHANG Li-ming. Intelligent vision image processing—Multi-channel image of unsupervised learning methods and other methods[M]. Shanghai: Shanghai Science and Technology Education Press, 2002.

[7] Hyvarinen A. Fast and robust fixed-point algorithm for independent component analysis[J]. IEEE Transactions on Neural Network, 1999, 10(3): 626-634.

[8] von Hoff T P, Lindgren A G, Kaelin A N. Step-size control in blind sourcec separation[C]//Proceedings of ICABSS’2000. Helsinki, 2000: 509-513.

[9] 方建斌, 李自玲, 管琼. 具有三阶收敛的“牛顿类”迭代法[J]. 武汉大学学报, 2009, 31(3): 398-400.
FANG Jian-bin, LI Zi-ling, GUAN Qiong. “Newton Like” iteration method with third-order convergence[J]. Journal of Wuhan University, 2009, 31(3): 398-400.

[10] 丁丽娟. 数值计算方法[M]. 北京: 北京理工大学出版社, 1997.
DING Li-juan. Numerical methods[M]. Beijing: Beijing Institute of Technology Press, 1997.

[11] 施光燕, 钱伟懿, 庞丽.最优化方法[M]. 2版. 北京: 高等教育出版社, 2007.
SHI Guang-yan, QIAN Wei-yi, PANG Li. Optimization methods[M]. 2nd ed. Beijing: Higher Education Press, 2007.

[12] Paraschiv-Ionescu A, Jutten C, et al. Wavelet denoising for highly noisy source separation[C]//Proceedings of IEEE International Symposium on Circuits and Systems (ISCA’02), 2002: 1201-1203.

(编辑 陈卫萍)

收稿日期：2011-04-15；修回日期：2011-06-15

基金项目：国家自然科学基金联合资金资助项目(10878017)

通信作者：胡祥楠(1982-)，男，辽宁新民人，硕士研究生，从事盲信号处理研究；电话：18242730980；E-mail：huxiangnan121@163.com