非均匀噪声分布心电信号的奇异值小波消噪法
刘雄飞,郭 爽, 李长庚,徐 飞
(中南大学 物理科学与技术学院,湖南 长沙,410083)
摘 要:针对一般消噪法对噪声非均匀分布心电信号消噪存在的不足,提出基于奇异值分解和小波阈值消噪相结合的消噪方法。该方法利用矩阵的奇异值分解将噪声非均匀分布的心电信号正交分解为噪声分布相对均匀的分量,在正交子空间中对每个分量进行小波阈值消噪,重构消噪后分量,得到消噪后的心电信号。研究结果表明:本方法有效地克服了因噪声分布不均匀而造成的小波阈值选择矛盾的缺点,有效地消除了大噪声区域的噪声,又完好保存小噪声区域的心电特征信息,且消噪后的信号与无噪信号之间的欧氏距离最小。
关键词:奇异值分解;小波阈值消噪;心电信号;噪声非均匀分布
中图分类号:TP274 文献标识码:A 文章编号:1672-7207(2009)05-1374-07
De-noising method for electrocardiograph of non-uniform noise distribution
based on singular value decomposition and wavelet transform
LIU Xiong-fei, GUO Shuang, LI Chang-geng, XU Fei
(School of Physics Science and Technology, Central South University, Changsha 410083, China)
Abstract: Aimed at the deficiency of common de-noising method for ECG (electrocardiograph) of non-uniform noise distribution, a de-noising method, which is based on singular value decomposition and wavelet transform, was proposed. ECG of non-uniform noise distribution was decomposed into several orthogonal-components, which had comparatively uniform noise, by singular value decomposition. Each component was de-noised by wavelet threshold de-noising method and de-noising ECG was obtained by rebuilding de-noised orthogonal-components. The results show that the proposed method can avoid the inconsistency of threshold choosing, which is caused by noise uneven distribution, the proposed method can de-noise thoroughly in big noise part and completely preserve the features of ECG in small noise part, and the Euclid distance between de-noised signal and non-noise signal is the least.
Key words: singular value decomposition; wavelet threshold de-noising; electrocardiograph; non-uniform noise distribution
心电信号的监测和分析是判断心脏功能状况、辅助诊断的主要手段,然而,心电信号是毫伏级的微弱信号,容易受到噪声的干扰如工频干扰、基线漂移干扰和肌电干扰等。Ahlstrom等[1]用低通滤波器法进行心电信号消噪,然而,低通滤波器只是滤除高频信息,对心电信号消噪的效果并不理想。Donoho等[2-3]采用小波阈值法进行心电信号的噪声处理。小波变换具有提供多方位、多层次的动态分析能力,去噪效果良 好[4]。小波阈值消噪的关键是阈值的选择,于是,出现了Nomannowsky准则和sure无偏估计[5-6]等自适应小波阈值计算的改进小波阈值算法[7-8]。它们对噪声分布均匀信号具有良好的消噪效果,但是,对于噪声非均匀分布信号具有局限性。奇异值分解消噪法是一种基于主分量分解的消噪方法[9],它对周期性正弦分量有很好的效果,但是,对心电信号等冲击性分量消噪效果不好。奇异值和小波双重消噪法对噪声具有双重消噪的效果[10],但是,仍然具有小波阈值消噪对噪声非均匀分布信号和奇异值对冲击信号消噪的局限性。小波系数矩阵奇异值消噪法能提取淹没在噪声中的特征信号[11-12],更适合于微弱特征信号的提取,而对于强特征的心电信号,消噪效果不明显。观察麻省理工学院心电信号数据库(MIT-BIH)中的大部分心电信号发现,有部分心电信号因受到环境、人和仪器的影响具有噪声非均匀分布现象,在此,本文作者提出基于奇异值分解和小波阈值消噪相结合的消噪方法。该方法利用矩阵奇异值正交分解和小波阈值消噪特点,以便解决非均匀噪声分布心电信号的消噪问题。
1 非均匀噪声分布心电信号的分解
1.1 矩阵奇异值分解理论
引理1 矩阵的奇异值理论:对于任何m×n阶矩阵A(其中,m>n)都存在以下分解[13]:

由式(2)和(3)可得出推论1。
推论1 矩阵奇异值分解是将矩阵分解为两两相互正交的子矩阵的叠加。
1.2 心电信号的奇异值分解
由于心电信号是一维信号,因此,在进行奇异值分解之前,需将一维信号转变成矩阵形式。
定义1 对于长度为N的一维信号,取2个正整数m和n,将序列截取m段长度为n个点的连续序列构成m×n阶矩阵,此方法称为一维信号的矩阵化。

心电信号经过奇异值分解后可表示为多个一维分量的叠加,且分量之间相互正交。噪声分布不均匀的心电信号经过奇异值的正交分解后,可有效地将噪声信号相对均匀地分解到子空间中。
2 分解分量的小波阈值消噪
小波变换是由短时傅里叶变换发展起来的,具有时频局部化和多分辨率的特性,其多分辨率公式为[16]:
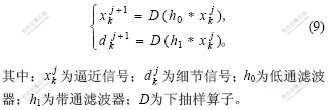
其重构公式为:
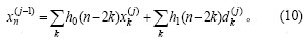
小波变换是信号与小波函数之间的内积运算,它具有多分辨率功能,将信号分解到不同的频带空间;它又具有时频局部化功能,能够表征信号的时间特性。
小波阈值消噪方法分为硬阈值法和软阈值法。硬阈值是将大于阈值的点保持不变,而软阈值法将大于阈值的点变为该点与阈值的差。由硬阈值法处理所得信号比由软阈值处理后所得信号更粗糙,因此,本文选择软阈值法。2种方法的消噪函数为:
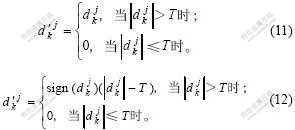
对于小波阈值消噪法,小波阈值选择规则有rigrsure,heursure,sqtwolog和minimaxi等。其中,minimax和rigrsure阈值选择规则比较保守、方便,不容易丢失真实信号成分,可以将弱小信号从高频信号中提取出来。而heursure和sqtwolog规则能够有效地去除噪声,但是,也可能将有用的高频信号当成噪声去除。Fix form threshold规则是一种折中的规则。
对噪声分布均匀的信号,以上规则具有良好的消噪效果,但是,对于噪声分布不均匀的信号,因信号不同,区域噪声分布特征不同,规则的选择相互矛盾,因此,本文将非均匀噪声分布心电信号经过奇异值分解,然后,利用小波软阈值消噪法分别对分解后的正交分量Si(1<i<k)进行消噪,由线性叠加消噪后的分量得出消噪后的心电信号。
3 心电信号的奇异值小波消噪法
噪声非均匀分布心电信号的奇异值小波消噪法步骤如下。
a. 将噪声非均匀分布心电信号经奇异值分解,得不同正交子空间的叠加:X=S1+S2+…+Sk。
b. 对若干个不同子空间的正交分量Si(1<i<k)采用小波阈值消噪法进行消噪,得到消噪后的分量S′i (1<i<k)。
c. 经过线性叠加消噪后的正交分量为:X′=S′1+S′2+…+S′k。其中:X′为消噪后心电信号。
奇异值小波消噪法的过程流程图如1所示。
4 消噪仿真及结果分析
4.1 心电信号消噪仿真
取MIT-BIH噪声信号库(MIT-BIH noise stress test database)中118e18信号的前3 000个点,采样周期为300点/s,其波形如图2所示。
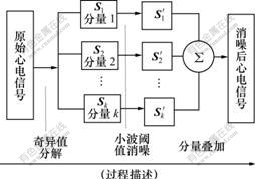
图1 奇异值小波消噪流程图
Fig.1 Flow chart of singular value decomposition wavelet de-noising
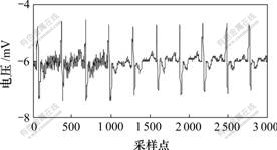
图2 噪声分布不均匀心电信号
Fig.2 Electrocardiograph of un-uniform noise distribution
图2所示心电信号为噪声非均匀分布的心电信号,其中,前1 000个采样点的噪声明显大于后2 000个采样点的噪声。首先,将心电信号构造成2行矩阵后进行奇异值分解,得到2个分量信号,如图3所示。
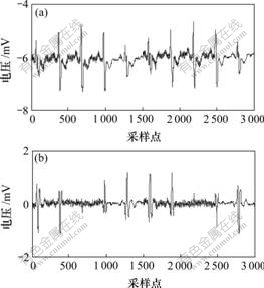
(a) 分量1;(b) 分量2
图3 奇异值分解后的正交分量
Fig.3 Orthogonal components of singular value decomposition wavelet
将图3中的分量1和分量2分别采用MATLAB 7.0 中的db3小波进行4层小波分解,然后,利用小波工具箱中的Fixed form threshold阈值选择策略进行软阈值消噪。线性叠加消噪后的分量1和分量2经奇异值小波消噪后,其波形如图4(c)所示。为了体现本方法对直接小波阈值法的改进效果,本文将噪声分布不均匀心电信号采用直接小波阈值消噪法进行消噪,与奇异值小波法进行比较,采用MATLAB 7.0中的db3小波4层分解和Fixed form threshold阈值选择策略,消噪后的心电信号如图4(b)所示。
图4(a)所示是噪声分布不均匀心电信号。由图4(a)可知,噪声分布不均匀心电信号的前1 000个采样点噪声明显高于后2 000个采样点的噪声。图4(b)所示的波形是小波阈值法消噪后的结果,可见,噪声分布不均匀,消噪后心电信号前1 000个采样点噪声较大,很难判断心电信号P波和T波的具体位置。对于后 2 000个采样点的心电信号,PQRST波的波峰经消噪后过于平滑,且波幅也略失真。图4(c)所示的波形是经奇异值小波消噪后的结果,可见,1 000个采样点的心电信号其PQRST波的基本特征清晰可辨,后2 000个采样点信号波峰和幅值的损失较小。由图4可知,对于噪声分布不均匀的心电信号,奇异值小波消噪法具有良好的消噪效果。
4.2 仿真结果分析
小波阈值消噪法的关键是对阈值进行选择,方法有:使用Stein的无偏似然估计原理进行阈值选择,启发式阈值选择,极大极小原理阈值选择,自适应阈值选择,等等。但是,这些阈值的选择只是针对噪声分布均匀的信号,对于噪声分布不均匀的信号其阈值选择存在一定的矛盾,若阈值过小,则噪声大部分信号消噪不彻底,若阈值过大,则噪声小部分信号出现波幅失真。如图4(a)所示,对噪声非均匀分布心电信号进行db3小波4层分解,采用Fixed form threshold阈值选择策略得阈值为0.081,其前3层高频信号和阈值线如图5所示。
由图5可知,因噪声分布不均匀,使得阈值比前1 000个采样点的阈值太小,而后2 000个采样点阈值太大,因此,导致前部分消噪不彻底,后部分消噪过多出现失真现象(见图4(b))。
奇异值小波法针对噪声非均匀分布信号首先进行奇异值分解,将信号正交分解为多个子空间信号叠加,相应的噪声信号也被正交分解到子空间中。由图3和图4可知,噪声非均匀分布信号经过奇异分解后其噪声分布比较均匀。对图3中2个分量信号分别进行db3小波4层分解和Fixed form threshold阈值选择策略,2个分量各层高频信号及阈值如图6所示。

(a) 噪声分布不均匀心电信号;(b) 小波阈值消噪后心电信号;(c) 奇异值小波消噪后心电信号
图4 奇异值小波阈值与小波阈值的消噪波形
Fig.4 De-noising wave of SVD-wavelet method and wavelet threshold method
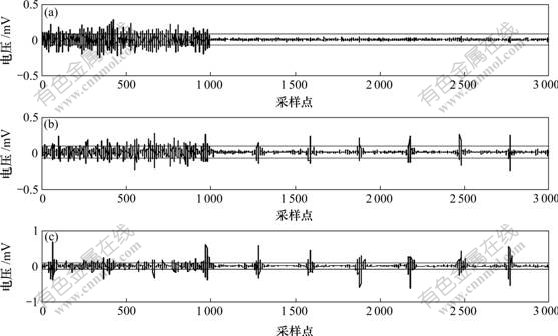
(a) 第1层;(b) 第2层;(c) 第3层
图5 小波阈值降噪的各高频信号
Fig.5 High frequency signals of wavelet threshold method
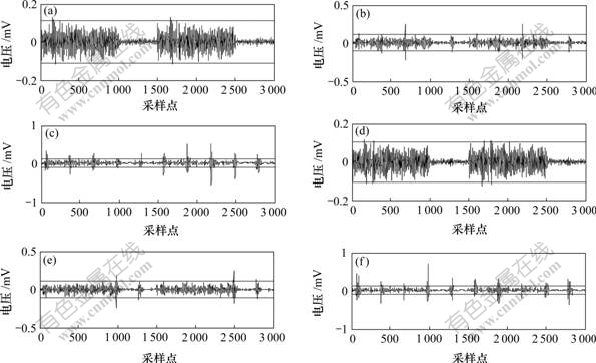
(a) 分量1第1层高频信号;(b) 分量1第2层高频信号;(c) 分量1第3层高频信号;(d) 分量2第1层高频信号;(e) 分量2第2层高频信号;(f) 分量2第3层高频信号
图6 分量信号小波阈值降噪各高频信号
Fig.6 High frequency signals of components by wavelet threshold method
分量1阈值计算结果为0.109,分量2的阈值计算结果为0.102。由图6可知,分量1和2阈值的选取比较合理,能够把噪声信号消去,且能够较完整地保留有用信息。因此,奇异值结合小波阈值消噪法对噪声分布不均匀信号具有良好的消噪效果。
4.3 本方法与其他方法的对比
基于MIT-BIH心律失常数据库中103信号的前 3 000个采样点,对其人为地添加非均匀白噪声。原始信号和加噪信号如图7所示。
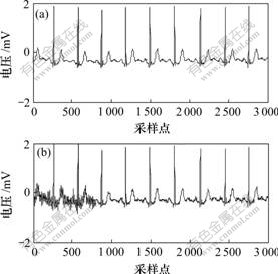
(a) 原始无噪信号;(b) 添加噪声信号
图7 原始信号和加噪信号
Fig.7 Original signal and added noise signal
分别采用本文方法(即奇异值小波消噪法)、自适应小波阈值消噪法、小波奇异值双重消噪法和小波系数矩阵奇异值变换消噪法进行消噪,消噪结果为采样点200~1 400的波形,如图8所示。由图8可知,这4种方法在800~1 400采样点处消噪差别不太大,但是,在200~800采样点之间的差异较大。奇异值小波消噪法的消噪能力明显比自适应小波法、小波矩阵奇异值变换法和小波奇异值双重法的消噪能力强,后3种方法都没有克服对非均匀分布噪声信号消噪的缺点。
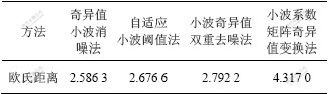
采用欧氏距离反映经各种方法消噪后心电信号与无噪声信号之间的差异,从而对比几种方法消噪方法的整体消噪效果。采用各种方法所得的欧氏距离如表1所示。可见,采用奇异值小波法所得的欧氏距离最小,因此,经奇异值小波法消噪后的心电信号失真性最小。
表1 采用4种方法所得欧氏距离的比较
Table 1 Comparison of Euclid distance for four methods
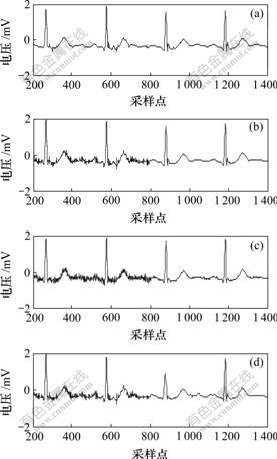
(a) 奇异值小波消噪法;(b) 自适应小波阈值法;(c) 小波矩阵奇异值变换法;(d) 小波奇异值双重法
图8 各种方法的消噪波形
Fig.8 De-noising wave of different methods
5 结 论
a. 对噪声非均匀分布的心电信号,奇异值小波消噪法克服了一般方法存在阈值选择的矛盾,提供了合理的阈值。
b. 对于噪声非均匀分布的心电信号,奇异值小波消噪法能够对大噪声区域消噪,且较完好保留小噪声区域信号的特征。
c. 与自适应小波阈值法、小波奇异值双重消噪法和小波系数矩阵奇异值变换消噪法相比,采用本文作者所提出的奇异值小波消噪法消噪,其噪声非均匀分布心电信号失真最小。
参考文献:
[1] Ahlstrom M L, Tompkins W J. Digital filters for real-time ECG signal processing using microprocessors[J]. IEEE Transaction on Biomedical Engineering, 1985, 32(9): 708-713.
[2] Donoho D L. Denoising by soft-threshholding[J]. IEEE Trans on Information Theory, 1995, 8(3): 613-627.
[3] 张泾周, 寿国法, 戴冠中. 基于小波变换的心电信号噪声处理[J]. 西北工业大学学报, 2005, 23(1): 11-14.
ZHANG Jing-zhou, SHOU Guo-fa, DAI Guan-zhong. Denoising of ECG signals based on wavelet transform[J]. Journal of Northwestern Polytechnic University, 2005, 23(1): 11-14.
[4] 袁修贵, 王 军, 黄修建, 等. 基于小波变换的一种图像增强去噪算法[J]. 中南大学学报: 自然科学版, 2005, 36(2): 298-301.
YUAN Xiu-gui, WANG Jun, HUANG Xiu-jian, et al. An improved algorithm of image de-noise and enhancement using wavelet transform[J]. Journal of Central South University: Science and Technology, 2005, 36(2): 298-301.
[5] 曲天书, 戴逸松, 王树勋. 基于SURE无偏估计的自适应小波阈值去噪[J]. 电子学报, 2002, 30(2): 266-268.
QU Tian-shu, DAI Yi-song, WANG Shu-xun. Adaptive wavelet thresholding denoising method based on SURE estimation[J]. Acta Electronica Sinica, 2002, 30(2): 266-268.
[6] Zhang X P, Desai M D. Adaptive denoising based on SURE risk[J]. IEEE Signal Processing Letters, 1998, 5(10): 265-267.
[7] 刘守山, 杨辰龙, 李 凌, 等. 基于自适应小波阈值的超声信号消噪[J]. 浙江大学学报: 工学版, 2007, 41(9): 1557-1560.
LIU Shou-shan, YANG Chen-long, LI Ling, et al. Adaptive wavelet shareholding based ultrasonic signal denoising[J]. Journal of Zhejiang University: Engineering Science, 2007, 41(9): 1557-1560.
[8] 罗志增, 张清菊, 蒋静坪. 表面肌电信号的小波消噪改进算法[J]. 浙江大学学报: 工学版, 2007, 41(2): 213-220.
LUO Zhi-zeng, ZHANG Qing-jun, JIANG Jing-ping. Improving method for surface electromyography denoising based on wavelet transform[J]. Journal of Zhejiang University: Engineering Science, 2007, 41(2): 213-220.
[9] 胡谋法, 董文娟, 王书宏, 等. 奇异值分解带通滤波背景抑制和去噪[J]. 电子学报, 2008, 36(1): 111-116.
HU Mou-fa, DONG Wen-juan, WANG Shu-hong, et al. Singular value decomposition band-pass filter for image background suppression and denoising[J]. Acta Electronica Sinica, 2008, 36(1): 111-116.
[10] 段礼详, 张来斌, 王朝晖, 等. 柴油机振动信号的小波包奇异值降噪[J]. 中国石油大学学报: 自然科学版, 2006, 30(1): 93-97.
DUAN Li-xiang, ZHANG Lai-bin, WANG Zhao-hui, et al. De-noising of diesel vibreation signal using wavelet packet and singular value decomposition[J]. Journal of China University of Petroleum, 2006, 30(1): 93-97.
[11] 梁 霖, 徐光华, 侯成刚. 基于奇异值分解的连续小波消噪方法[J]. 西安交通大学学报, 2004, 38(9): 904-908.
LIANG Lin, XU Guang-hua, HOU Cheng-gang. Continuous wavelet transform denoising method based on singular value decomposition[J]. Journal of Xi’an Jiaotong University, 2004, 38(9): 904-908.
[12] 张建伟, 鲍 政, 王顺凤. 图像小波域分块奇异值分解的自适应水印方案[J]. 中国图像图形学报, 2007, 12(5): 811-818.
ZHANG Jian-wei, BAO Zheng, WANG Sun-feng. Adaptive image watermarking scheme based on the wavelet domain SVD[J]. Journal of Image and Graphics, 2007, 12(5): 811-818.
[13] Akritas A G, Malaschonok G I. Application of singular value decomposition[J]. Mathematics and Computers in Simulation, 2004, 67(1): 15-31.
[14] Vrabie V D, Mars J I, Lacoume J L. Modified singular value decomposition by means of independent component analysis[J]. Signal Processing, 2004, 84(3): 645-652.
[15] 赵学智, 陈统坚, 叶邦彦. 基于奇异值分解的铣削力信号处理与铣床状态信息分离[J]. 机械工程学报, 2007, 43(6): 169-174.
ZHAO Xue-zhi, CHEN Tong-jian, YE Bang-yan. Processing of milling force signal and isolation of state information of milling machine based on singular value decomposition[J]. Chinese Journal of Mechanical Engineering, 2007, 43(6): 169-174.
[16] Berkner K, Wells R O. Wavelet transforms and denoising algorithms[C]//Conference Record of the Thirty-second Asilomar Conference. Signals Systems and Computers, 1998, 2: 1639-1643.
收稿日期:2008-10-10;修回日期:2008-12-20
基金项目:湖南省科技计划项目(2007FJ3066)
通信作者:刘雄飞(1960-),男,湖南长沙人,教授,从事数字信号处理研究;电话:0731-88836331;E-mail: x.f.liu@163.com