Trans. Nonferrous Met. Soc. China 27(2017) 1645-1655

Effect of inlet configuration on hydrocyclone performance

Bo TANG, Yan-xia XU, Xing-fu SONG, Ze SUN, Jian-guo YU

National Engineering Research Center for Integrated Utilization of Salt Lake Resource, East China University of Science and Technology, Shanghai 200237, China

Received 29 March 2016; accepted 18 September 2016

Abstract: Inlet configuration is important parameter of hydrocyclones, which has great impact on the classification performance. The effects of inlet configuration on the precise classification were studied by computational fluid dynamics under various combinations of inlet diameter and inlet velocity. The results showed that a high sharpness of classification was achieved with specific inlet diameter and inlet velocity. The separation efficiency of the coarse particles by underflow significantly decreased when inlet had an oversize diameter owing to a stronger short-circuit flow. It is resulted from the chaotic flow and the stronger pressure gradient around the vortex finder. Meanwhile, a low separation efficiency of the fine particles by overflow was achieved when inlet velocity was high, which indicated a low sharpness caused by the overlarge centrifugal force.

Key words: hydrocyclone; inlet configuration; separation sharpness; computational fluid dynamics

1 Introduction

Hydrocyclones [1-3] are one of the most important liquid–solid classification devices, which are widely used in many industrial fields. Suspended particles can be classified owing to the comprehensive force field inside a hydrocyclone. The larger or heavier particles are collected by the underflow because of the higher centrifugal force, whereas the smaller or lighter particles are separated through the overflow with most of the fluid. As efficient centrifugal separation equipment, a hydrocyclone has specific features such as a large capacity, a small physical size, low production and maintenance costs, and strong adaptability to harsh conditions. To date, the developments in different industries [4,5] have attracted much attention for the precise classification of solid suspended particles from continuous liquid phase. Therefore, studies on the classification of particles with a high sharpness using hydrocyclones gradually became an area of high research interest.

The hydrodynamic behaviors in hydrocyclones consist of the outer and inner swirling flow, air core, short-circuit flow, and boundary flow [6-8]. To achieve satisfactory performance of classification with a high sharpness, a series of studies have been carried out to evaluate the effects of flow behaviors [9-11]. Correspondingly, numerous suggestions for optimizing the structural parameters of hydrocyclone have been proposed. Some studies [12,13] showed that the flow field inside a hydrocyclone will become more stable in the absence of an air core. And a more precise separation process can be achieved by inserting a solid rod along the central axis of a hydrocyclone [14]. The investigations [15,16] showed that the percentage of coarse particles discharged into the overflow directly increased by a stronger short-circuit flow. New configurations of vortex finder were designed to reduce the adverse effects of a short-circuit flow [17,18]. Moreover, the entrainment of fine particles in the underflow will decrease the sharpness of classification. Therefore, numerous schemes [19-21] for displacing the feed in underflow have been proposed.

Since the tangential entrance [22,23] is a key point affecting the hydrodynamic behaviors of hydrocyclones, more attention has been paid to optimizing the inlet configuration. Some results [24-26] showed that the symmetrical inlets improved the classification sharpness in hydrocyclones. However, the mechanism between the inlet configuration and hydrocyclone performance was not fully understood. The investigation of CHU et al [27] showed that the tangential inlet had the highest sharpness of separation among different inlet types. Meanwhile, the study of QIAN et al [28,29] concluded that an optimized inlet section angle could improve the separation efficiency. But the complex manufacturing process of new inlet configurations has limited its applications in industry. To further improve the performance of hydrocyclones, it is of practical significance to understand the mechanism of inlet configurations on the efficiency and sharpness of separation.

In this work, numerical method has been proposed to elucidate the effects of inlet configurations on the classification performance of hydrocyclones. The results were used to understand the mechanism influencing the sharpness with the variation of inlet diameter and inlet velocity. Furthermore, the hydrocyclone with optimized inlet configuration was applied for the high sharpness classification.

2 Experimental

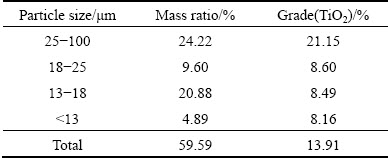
In the production process of titanium dioxide by the sulfate method, the hydrocyclone is applied for the classification of tailings after the unit operation of acid leaching. The slurry consisting of unreacted ilmenite and impurity minerals is injected into the hydrocyclone, and the particles with different diameters can be classified by the centrifugal force. By analyzing the chemical components of tailing samples, the objective of the separation can be determined. As shown in Table 1 [30], 40.41% of the particles dissolved in water by a series of wet sieving. In the rest of tailings, the particles larger than 25 μm contain 21.15% of TiO₂, which should be enriched by the spigot. The particles smaller than 25 μm are composed of mostly impurities, which should be separated through the vortex finder.

Table 1 Particle size, mass ratio and component analyses of tailings

2.1 Mathematical model

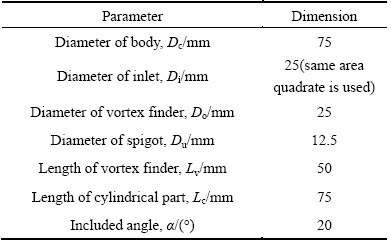
A hydrocyclone of 75 mm in diameter was used in this study, as shown in Fig. 1(a). Table 2 shows the geometrical details of the hydrocyclone. To study the effects of inlet configurations on the performance of hydrocyclones, the value of Re was set in the range of 22840-90465 with different inlet diameters (D_i/D_c= 0.20-0.40) and inlet velocities (v=1.28-3.03 m/s). Reasonable models play an important role in describing the swirling multiphase flow in a hydrocyclone. The Reynolds stress model (RSM) was used to predict the strong rotating flow considering the anisotropic nature of turbulence. The air core in a hydrocyclone is a free surface between the continuous phases of water and air. In this situation, the volume of fluid (VOF) model is suitable to model the air core. An implicit scheme of the VOF model was used to calculate the volume fraction of each of the two phases. For further evaluating the grade efficiency, the stochastic Lagrangian model was used because of the low volume fraction of solid phase. A two-way coupling was considered to predict the dispersion of particles considering the effects of turbulence in the fluid. More details of the models are given elsewhere [30,31].

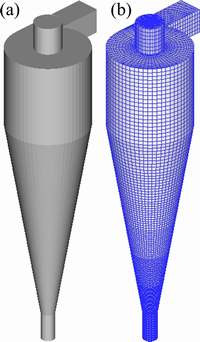
Fig. 1 Dimension (a) and grid (b) diagrams of d75 mm hydrocyclone

Table 2 Geometry of basic d75 mm hydrocyclone

The pressure equation was discretized by PRESTO, which is the most suitable algorithm for a high-speed swirling flow [32]. The SIMPLE algorithm was used for the coupling of pressure and velocity [33]. A second-order upwind scheme was used for the spatial discretization of momentum, volume fraction, turbulent kinetic energy, and dissipation rate, as well as for Reynolds stresses. The convergence strategy used the unsteady solver, and the 10^-3 accuracy of convergence criterion was used. In this study, the time step was set as 5×10^-4 s.

2.2 Simulation conditions

The “velocity inlet” boundary condition was used at the inlet of a hydrocyclone. Both the vortex finder and spigot were set as the “pressure outlet” boundary condition, and the pressure at the two outlets was 1.0×10⁵ Pa. Figure 1(b) shows the meshed computational domain of the hydrocyclone, and the origin of the coordinates was set at the center on the interface between the section of cylinder and cone. The entire hydrocyclone was divided by hexahedron grids. A grid independence test was conducted with mesh sizes varying from 97000 to 301000, and the validation results show that 259000 cells were optimal for the balance of prediction accuracy and computational cost.

It was assumed that 25000 particles of tailings are released into a hydrocyclone with the same velocity as the fluid and evenly distributed over the entire entrance surface. The volume percentage of tailings was 1.7% in the feed; therefore, it was reasonable to apply the stochastic Lagrangian model for calculating the grade efficiency. The size distribution of the particles was measured using a Malvern Mastersizer 2000. Figure 2 shows that all the particles were smaller than 100 μm. The size distribution was fitted by the Rosin–Rammler model for simulation. The mean diameter of particles was 19.85 μm, and the parameter of distribution was 1.26. Furthermore, the density for simulation was set as 2057.9 kg/m³, according to the measurement data.

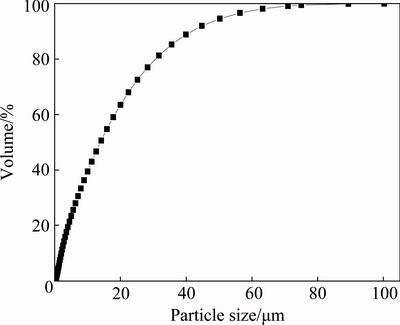
Fig. 2 Particle size distribution of acid leaching tailings

2.3 Performance indices

The performance of hydrocyclones was evaluated by the following indices: 1) split ratio (S); 2) pressure drop (Δp); 3) separation efficiency (E_T); 4) separation sharpness (K).

Split ratio (S) means the partition ratio of fluid, which is defined as follows:

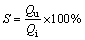                              (1)

where Q_u and Q_i are mass flow rates of fluid from the spigot and the inlet, respectively.

Pressure drop (Δp) between the inlet and the vortex finder is as follows:

△p=p_i-p_o                                (2)

where p_i and p_o are pressures of the inlet and the vortex finder, respectively.

Separation efficiency (E_T) is defined as follows:

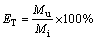                            (3)

where M_u and M_i are mass flow rates of particles from the spigot and the inlet, respectively.

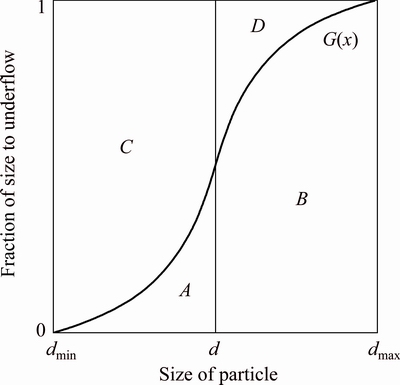
Fig. 3 Schematic diagram of indices of separation sharpness

As shown in Table 1, the hydrocyclone aims at a higher recovery of particles that are larger than 25 μm through the spigot and a better separation efficiency of the rest of the particles by the vortex finder. Therefore, the sharpness index of separation of tailings can be defined as follows:

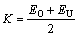                               (4)

where E_O and E_U are described in more details as follows:

As shown in Fig. 3, the specific definition of E_O and E_U is as follows:

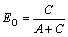                                 (5)

where A represents the amount of particles that are smaller than 25 μm collected by the spigot, and C represents the amount of particles that are smaller than 25 μm separated by the vortex finder. Therefore, E_O is the percentage of particles that are smaller than 25 μm, separated by the vortex finder. Meanwhile, E_U is defined in the same manner, as the percentage of particles that are larger than 25 μm collected by the spigot.

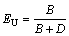                                 (6)

where B represents the amount of particles that are larger than 25 μm collected by the spigot, and D represents the amount of particles that are larger than 25 μm separated by the vortex finder.

2.4 Simulation validation

Before the numerical study, the applicability of the used models was validated by comparing the predicted velocity profiles with the experimental data [34] at different axial locations. The predicted results of velocity field were consistent with the experimental data. Then, the grade efficiency of the particles was compared to the classification data, indicating a good qualitative agreement. Many works showed that the numerical models were validated to be capable for extending to different configurations [17,32]. More details have been shown in the previous study [2,30].

3 Results and discussion

3.1 Effects of inlet Reynolds number on performance

Inlet Reynolds number can be expressed as follows:

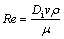                                 (7)

where D_i is inlet diameter, v is inlet velocity, ρ is the density, and μ is the molecular viscosity. Inlet Reynolds number, as the dimensionless group taking D_i and v into consideration, was chosen for inlet configuration.

Split ratio and pressure drop are important indices to characterize the operating state of hydrocyclones. A strong correlation was shown between split ratio and the hydrodynamics of swirling flow [35]. And pressure drop was used to evaluate the energy consumption. In this study, the effects of inlet Reynolds number on split ratio and pressure drop were evaluated, in the range of 22840-90465 with different inlet diameters and inlet velocities. As shown in Fig. 4, the overall trend of split ratio decreased sharply from the start, and then it became stable with the increase in inlet Reynolds number. It can be explained by the fact that the forced vortex motion was not fully developed when inlet Reynolds number was relatively small, and with the increase in inlet Reynolds number, the forced vortex motion became stable. However, three data points deviated from the line. The values of split ratio were higher than the trend when inlet Reynolds number was 45680, 59564, and 68073 (All D_i/D_c were 0.350 and 0.400). This phenomenon is the results of a stronger short-circuit flow caused by the oversize inlet diameter. On the other hand, a simple relationship may exist between inlet Reynolds number and pressure drop, as shown in Fig. 5. Pressure drop continuously increased by increasing inlet Reynolds number, indicating that more energy is required to maintain the separation process of hydrocyclones. It showed that a lower tangential velocity was probably caused by a smaller inlet Reynolds number, which weakened the vortex intensity and leaded to a lower pressure drop.

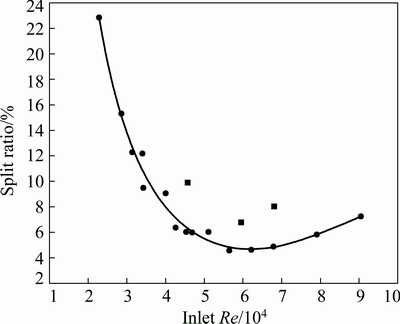
Fig. 4 Relationship between split ratio and inlet Re

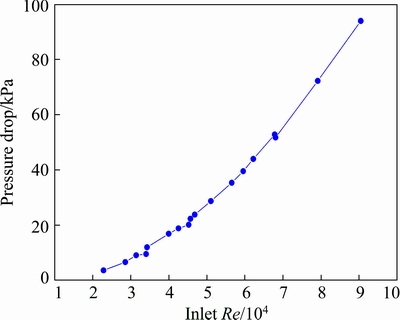
Fig. 5 Relationship between pressure drop and inlet Re

Figure 6 showed the effects of inlet Reynolds number on the separation performance of hydrocyclones. It could be concluded that cut size d₅₀ had a downward trend with the increase in inlet Reynolds number. To some extent, a smaller d₅₀ represents its good efficiency in solid-liquid separation. It showed that the centrifugal force exerted on the particles would increase by increasing inlet Reynolds number. However, as shown in Fig. 6, two points were smaller than the trend values and five points were larger than the trend ones. As shown in Table 3, compared to slightly higher and lower inlet Reynolds number, d₅₀ of two deviated points was low when inlet Reynolds number was made up of a larger velocity. And d₅₀ of five deviated points was high when inlet Reynolds number consisted of a relatively low inlet velocity or a relatively large inlet diameter. Further, the mechanism of inlet diameter and inlet velocity on the performance of hydrocyclones will be elucidated as described in Sections 3.2.1 and 3.2.2.

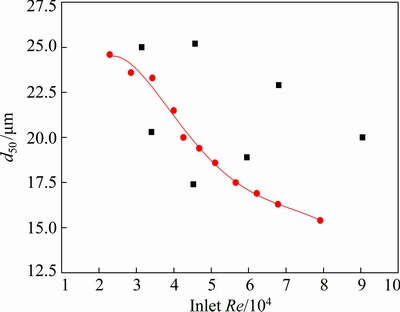
Fig. 6 Relationship between cut size d₅₀ and inlet Re

Table 3 lists the performance indices of hydrocyclones with different inlet Reynolds numbers. The effects of inlet Reynolds number on the classification sharpness can be evaluated by E_O and E_U. E_O was below 0.650 when the inlet Reynolds number was 45232, 56541, 62195, 67849, and 79157 (All inlet velocity was 3.03 m/s). Based on the above results, it could be concluded that the efficiency of the fine particles separated by vortex finder was governed by inlet velocity, and the mechanism behind the phenomenon was in Section 3.2.2. On the other hand, E_U could remain above 0.900 in most cases. Nevertheless, E_U would stay at a lower value when inlet Reynolds number was 39970, 45680, 68073, and 90465 (All D_i/D_c were 0.350 and 0.400). Notably, a stronger short-circuit flow will form when inlet diameter is relatively large, which was explained in detail in Section 3.2.1. Further, the effects of a short-circuit flow can be reduced by increasing inlet velocity, as shown when inlet Reynolds number was 59564 and 79157 (D_i/D_c was 0.350). When the particles were injected with a higher inlet velocity, they would move with a large radius because of the centrifugal effect, which were close to the wall of the hydrocyclone.

Table 3 Indices of hydrocyclone performance with different inlet Re

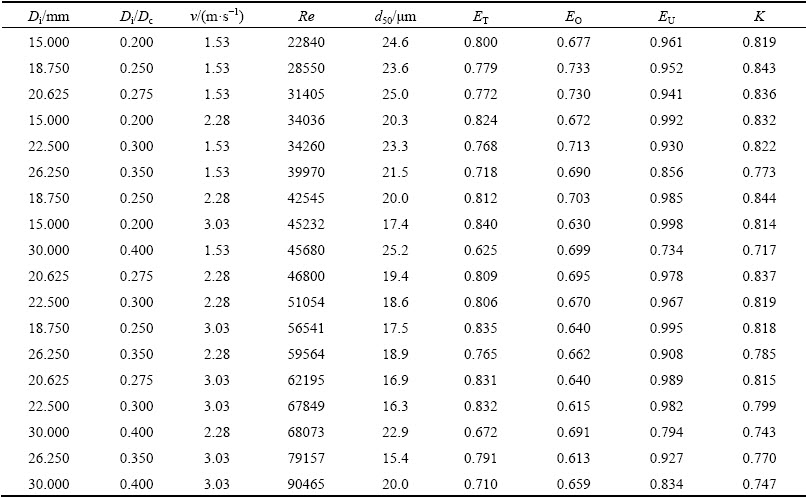
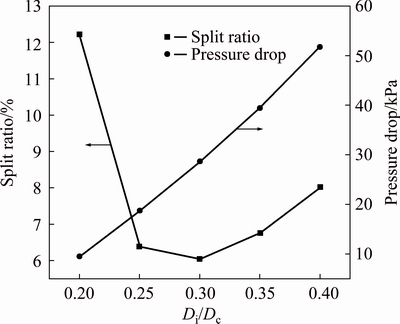
Fig. 7 Split ratio and pressure drop of d75 mm hydrocyclone

3.2 Mechanism of inlet diameter and inlet velocity on performance

3.2.1 Effects of inlet diameter

As shown in Fig. 7, for hydrocyclones where inlet velocity was constant at 2.28 m/s, split ratio decreased from 12.21% to 6.04% when D_i/D_c increased from 0.20 to 0.30, then split ratio slightly increased from 6.04% to 8.02% with a further increase in D_i/D_c. Figure 8 shows the profiles of velocity field in hydrocyclones with different D_i/D_c. The magnitude of upward axial velocity increased significantly when D_i/D_c increased from 0.20 to 0.30; consequently, a greater proportion of the fluid joined the forced vortex motion. However, the locus of zero vertical velocity (LZVV) moved closer to the hydrocyclone axis when D_i/D_c was increased from 0.30 to 0.40, causing a slight increase in split ratio. Figure 7 with different D_i/D_c also shows that pressure drop increased monotonically with increasing D_i/D_c. Based on the constant inlet velocity, more fluid was injected tangentially into the hydrocyclone with a larger inlet diameter, indicating that more energy would be consumed to maintain the separation process. Figure 8 also shows that a higher tangential velocity was created with the increase in D_i/D_c, leading to a higher pressure drop.

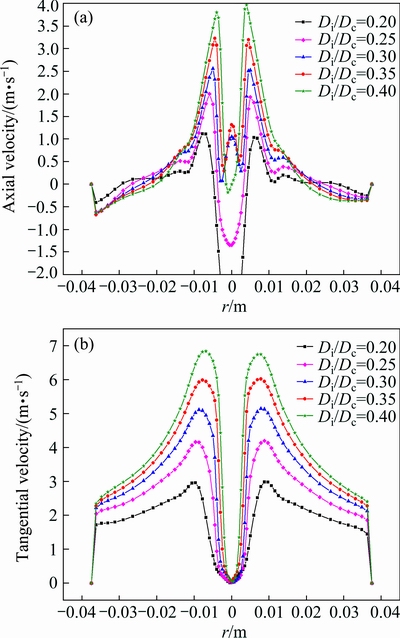
Fig. 8 Axial (a) and tangential (b) velocities at 60 mm from top with different D_i/D_c

Figure 9 shows the variation in the grade efficiency of particles when D_i/D_c ranged from 0.20 to 0.40. All the curves exhibited a fishhook phenomenon when particle size was below 5 μm. As shown in Fig. 9, the effects of inlet diameter on the grade efficiency of particles could be evaluated by two aspects. Firstly, for particles that are smaller than 20 μm, the grade efficiency would slightly change with the variation in D_i/D_c. It is well known that this part of particles showed a good following with the fluid in hydrocyclones, and because of the bypass effect, a higher split ratio led to the increase in the grade efficiency [36]. Secondly, once the particles are larger than 20 μm, it could be observed that inlet diameter significantly affected the grade efficiency, caused by the short-circuit flow. From an overall point of view, the grade efficiency for the coarse particles decreased with the increase in D_i/D_c. Nevertheless, particularly when D_i/D_c reached a critical value of 0.35, the grade efficiency for the coarse particles decreased severely, leading to a high percentage of the coarse particles escaped into the overflow.

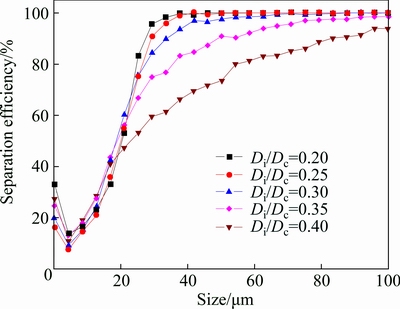
Fig. 9 Grade efficiency curves for d75 mm hydrocyclone with different D_i/D_c

Table 4 listed the performance indices of particle classification in hydrocyclones with different D_i/D_c. The percentages of the coarse particles collected by underflow could remain above 96.0% as D_i/D_c was in the range of 0.20-0.30. When D_i/D_c exceeded a critical value, equal to 0.35 in this study, the separation efficiency for the coarse particles decreased sharply. In the worst case, 20.6% of the coarse particles would be separated from overflow when D_i/D_c is 0.40. The analyses of flow field showed that the phenomenon was caused by a stronger short-circuit flow. Figure 10 showed the radial velocity contours on central vertical plane of hydrocyclones with different D_i/D_c. As indicated by point A, either a broader distribution area or a higher inward radial velocity could be observed near the bottom of vortex finder with the increase in D_i/D_c. Moreover, Fig. 11 showed the flow streamlines of the cylinder when D_i/D_c ranged from 0.30 to 0.40. The increase in D_i/D_c entailed the appearance of the short-circuit flow. When D_i/D_c was 0.35 or 0.40, the fluid had a larger trend to move along the surface of vortex finder. Table 5 showed the percentage of the coarse particles escaped by overflow shortly after they were injected into the hydrocyclone. The results confirmed that a considerable proportion of the coarse particles escaped from overflow without going through the separation process.

Table 4 Indices of hydrocyclone performance with different D_i/D_c

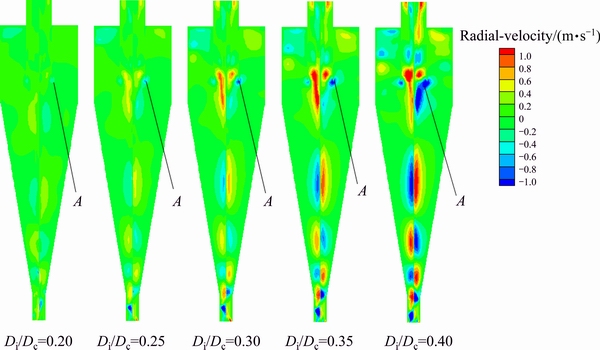
Fig. 10 Contours of radial velocity for d75 mm hydrocyclone with different D_i/D_c

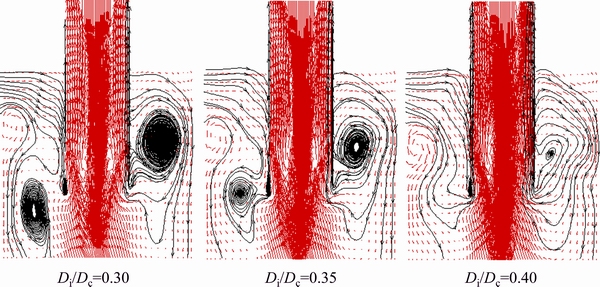
Fig. 11 Flow streamlines on central vertical plane of d 5 mm hydrocyclone with D_i/D_c ranging from 0.30 to 0.40

Table 5 Percentage of coarse particles escaped by overflow at t=0.0-0.3 s

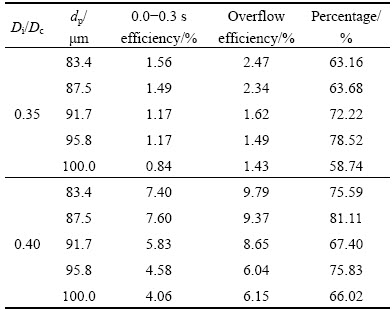
Figure 12 shows the profiles for velocity vector at axial position located at 5 mm from the roof. The fluid was injected tangentially into the hydrocyclone at 2.28 m/s, and as the fluid entered the cylinder, the velocity magnitude increased up to 1.0-2.0 times as inlet velocity. Moreover, a flow region of high velocity was formed close to the outer surface of vortex finder at point A. When the fluid moved downward along vortex finder, a chaotic flow region was formed because of the interactions between upward fluid and downward fluid. As a result, a proportion of the fluid would join the overflow, which was also shown in the research of WANG and YU [17]. Figure 13 showed the distribution of relative pressure on central vertical plane with D_i/D_c ranging from 0.30 to 0.40. It indicated that a stronger pressure gradient was formed as D_i/D_c increased, and a great proportion of the fluid would move towards the vortex finder along the inner wall directly. More percentage of the coarse particles would be trapped by the fluid without going through the separation process. This was probably the reason for a stronger short-circuit flow in hydrocyclones when D_i/D_c were 0.35 and 0.40.

3.2.2 Effects of inlet velocity

Effects of inlet velocity on the flow field in hydrocyclones were investigated with a certain D_i/D_c of 0.25. As shown in Fig. 14, split ratio decreased continuously as inlet velocity was increased from 1.28 to 3.03 m/s. Split ratio decreased significantly when inlet velocity was in the range of 1.28-2.03 m/s, and because of the slow rise of axial velocity, it became stable with a further increase to 3.03 m/s. Figure 15 explained that an increased inlet velocity improved the magnitude of upward axial velocity. However, it seemed that inlet velocity slightly affected the profile of LZVV. As a result, a larger proportion of fluid moved towards the vortex finder. On the other hand, pressure drop increased gradually with the increase in inlet velocity. As shown in Fig. 15, because of the higher magnitude of tangential velocity, the hydrocyclone would consume more energy by strengthening the vortex intensity.

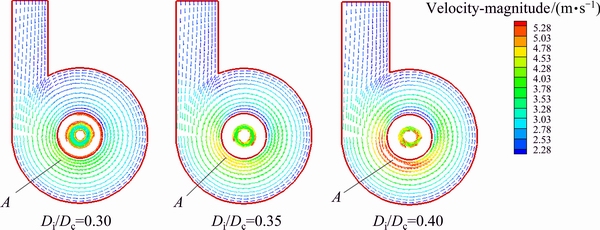
Fig. 12 Profiles for velocity vector located at 5 mm from top of d75 mm hydrocyclone with D_i/D_c ranging from 0.30 to 0.40

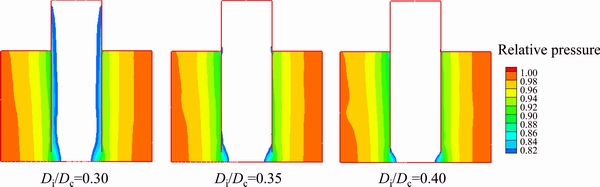
Fig. 13 Distribution of relative pressure on central vertical plane of d75 mm hydrocyclone with D_i/D_c ranging from 0.30 to 0.40

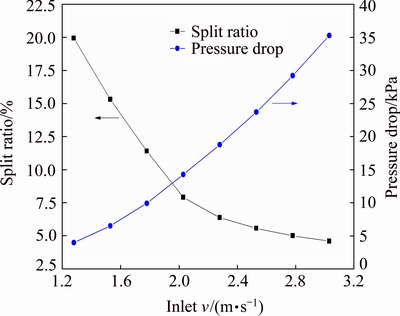
Fig. 14 Split ratio and pressure drop of d75 mm hydrocyclone with different inlet v

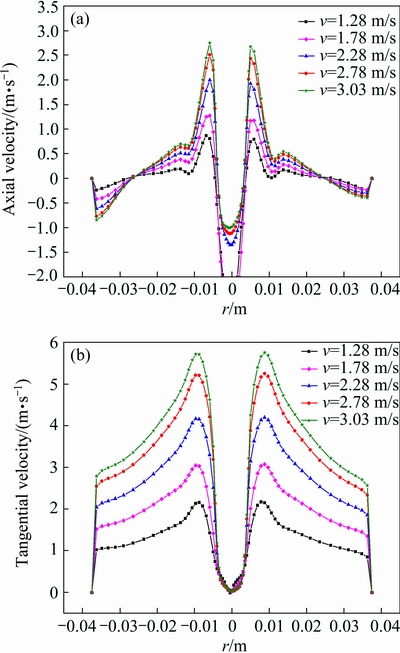
Fig. 15 Axial and tangential velocities at 60 mm from top with different inlet v

Figure 16 shows the comparison of grade efficiency of particles for the studied inlet velocity. For particles that are larger than 15 μm, the grade efficiency increased with the increase in inlet velocity. For the rest of particles, higher grade efficiency were achieved when inlet velocities were 1.28 and 1.78 m/s. Particles smaller than 15 μm showed a good following with the fluid in hydrocyclones, and a higher split ratio led to the increase in grade efficiency because of the bypass effect [36]. Further, it was shown that a series of inlet velocity did not change the fishhook phenomenon of all the curves.

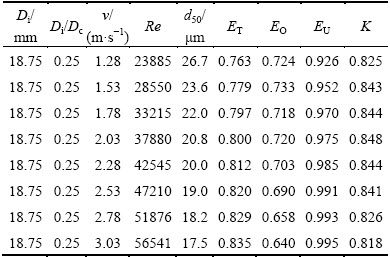
The classification performance with different inlet velocities could be evaluated by the indices listed in Table 6. An increasing E_T and a decreasing d₅₀ were observed with the increase in inlet velocity, which is beneficial for solid-liquid separation. The index K had a lower value when inlet velocity was at the extremes of its range. When inlet velocity was 1.28 m/s, a lower separation efficiency of the coarse particles by the underflow decreased the index K, as shown by a lower E_U. However, when inlet velocity exceeded a critical value, 2.78 m/s in this study, an increase in the tangential velocity would lead to a significant increase in the centrifugal force, then, the fine particles had more possibility to be trapped by the underflow. Therefore, the decrease of the index K was the result of a lower E_O. The index K of hydrocyclones maintained a high value when inlet velocity was in the range from 1.53 to 2.53 m/s.

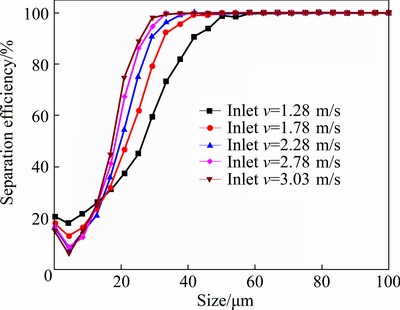
Fig. 16 Grade efficiency curves for d75 mm hydrocyclone with different inlet v

Table 6 Indices of hydrocyclone performance with different inlet v

4 Conclusions

1) The effects of inlet configurations on the sharpness of separation can be shown: First, when the inlet diameter exceeds a critical value, the decrease of the sharpness can be attributed to the larger fraction of the coarse particles separated by vortex finder; Second, when the inlet velocity is relatively high, the decrease of the sharpness was the result of a higher efficiency for the fine particles collected by spigot.

2) When the inlet diameter exceeded a critical value, a significant increase in the efficiency of the coarse particles by vortex finder decreased the sharpness. The decrease of the sharpness is essentially governed by a stronger short-circuit flow, which is resulted from a combined effect of the chaotic flow and stronger pressure gradient around the vortex finder.

3) The inlet velocity significantly affected the efficiency of the fine particles by spigot. A greater proportion of the fine particles were trapped by spigot with the increase of inlet velocity. The decrease of the sharpness is caused by a significant increase in the centrifugal force.

References

[1] WANG B, YU A B. Computational investigation of the mechanisms of particle separation and “Fish-Hook” phenomenon in hydrocyclones [J]. AIChE Journal, 2010, 56: 1703-1715.

[2] XU Y X, SONG X F, SUN Z, TANG B, LI P, YU J G. Numerical investigation of the effect of the ratio of the vortex finder diameter to the spigot diameter on the steady state of the air core in a hydrocyclone [J]. Industrial & Engineering Chemistry Research, 2013, 52: 5470-5478.

[3] WANG B, CHU K W, YU A B. Numerical study of particle-fluid flow in a hydrocyclone [J]. Industrial & Engineering Chemistry Research, 2007, 46: 4695-4705.

[4] YAMAMOTO T, SHINYA T, FUKUI K, YOSHIDA H. Classification of particles by centrifugal separator and analysis of the fluid behavior [J]. Advanced Powder Technology, 2011, 22: 294-299.

[5] KIM J S, KIM D H, GU B, KIM D Y, YANG D R. Simulation of Taylor-Couette reactor for particle classification using CFD [J]. Journal of Crystal Growth, 2013, 373: 106-110.

[6] LIU Y, YANG Q, QIAN P, WANG H L. Experimental study of circulation flow in a light dispersion hydrocyclone [J]. Separation Purification Technology, 2014, 137: 66-73.

[7] CUI Rui, WANG Guang-hui, LI Mao-lin. Size dependent flow behaviors of particles in hydrocyclone based on multiphase simulation [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 2422-2428.

[8] GAO Shu-ling, WEI De-zhou, LIU Wen-gang, MA Long-qiu, LU Tao, Zhang Rui-yang. CFD numerical simulation of flow velocity characteristics of hydrocyclone [J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 2783-2789.

[9] BAI Z S, WANG H L, TU S T. Experimental study of flow patterns in deoiling hydrocyclone [J]. Mineral Engineering, 2009, 22: 319-323.

[10] WANG Z B, CHU L Y, CHEN W M, WANG S G. Experimental investigation of the motion trajectory of solid particles inside the hydrocyclone by a Lagrange method [J]. Chemical Engineering Journal, 2008, 138: 1-9.

[11] BANERJEE C, CHAUDHURY K, MAJUMDER A K, CHAKRABORTY S. Swirling flow hydrodynamics in hydrocyclone [J]. Industrial & Engineering Chemistry Research, 2015, 54: 522-528.

[12] CHU L Y, YU W, WANG G J, ZHOU X T, CHEN W M, DAI G Q. Enhancement of hydrocyclone separation performance by eliminating the air core [J]. Chemical Engineering & Processing, 2004, 43: 1441-1448.

[13] SRIPRIYA R, KAULASKAR M D, CHAKRABORTY S, MEIKAP B C. Studies on the performance of a hydrocyclone and modeling for flow characterization in presence and absence of air core [J]. Chemical Engineering Science, 2007, 62: 6391-6402.

[14] EVANS W K, SUKSANGPANOMRUNG A, NOWAKOWSKI A F. The simulation of the flow within a hydrocyclone operating with an air core and with an inserted metal rod [J]. Chemical Engineeing Journal, 2008, 143: 51-61.

[15] CHU L Y, LUO Q. Hydrocyclone with high sharpness of separation [J]. Filtration & Separation, 1994, 31: 733-736, 720.

[16] MONREDON T C, HSIEH K T, RAJAMANI R K. Fluid flow model of the hydrocyclone: An investigation of device dimensions [J]. International Journal of Mineral Processing, 1992, 35: 65-83.

[17] WANG B, YU A B. Numerical study of the gas-liquid-solid flow in hydrocyclones with different configuration of vortex finder [J]. Chemical Engineering Journal, 2008, 135: 33-42.

[18] GHODRAT M, KUANG S B, YU A B, VINCE A, BARNETT G D, BARNETT P J. Numerical analysis of hydrocyclones with different vortex finder configurations [J]. Mineral Engineering, 2014, 63: 125-138.

[19] HONAKER R Q, OZSEVER A V, SINGH N, PAREKH B K. Apex water injection for improved hydrocyclone classification efficiency [J]. Mineral Engineering, 2001, 14: 1445-1457.

[20] DUECK J, PIKUSHCHAK E, MINKOV L, FARGHALY M, NEESSE T. Mechanism of hydrocyclone separation with water injection [J]. Mineral Engineering, 2010, 23: 289-294.

[21] FARGHALY M G, GOLYK V, IBRAHIM G A, AHMED M M, NEESSE T. Controlled wash water injection to the hydrocyclone underflow [J]. Mineral Engineering, 2010, 23: 321-325.

[22] AZADI M, AZADI M. An analytical study of the effect of inlet velocity on the cyclone performance using mathematical models [J]. Powder Technology, 2012, 217: 121-127.

[23] ELSAYED K, LACOR C. The effect of cyclone inlet dimensions on the flow pattern and performance [J]. Applied Mathematical Modelling, 2011, 35: 1952-1968.

[24] HWANG K J, HWANG Y W, YOSHIDA H. Design of novel hydrocyclones for improving fine particle separation using computational fluid dynamics [J]. Chemical Engineering Science, 2013, 85: 62-68.

[25] YOSHIDA H, YOSHIKAWA S, FUKUI K, YAMAMOTO T. Effect of multi-inlet flow on particle classification performance of hydro- cyclones [J]. Powder Technology, 2008, 184: 352-360.

[26] NENU R K T, YOSHIDA H. Comparison of separation performance between single and two inlets hydrocyclones [J]. Advanced Powder Technology, 2009, 20: 195-202.

[27] CHU L Y, CHEN W M, LEE X Z. Effect of structural modification on hydrocyclone performance [J]. Separation Purification Technology, 2000, 21: 71-86.

[28] QIAN F P, ZHANG M Y. Effects of the inlet section angle on the flow field of a cyclone [J]. Chemical Engineering Technology, 2007, 30: 1564-1570.

[29] QIAN F P, WU Y P. Effects of the inlet section angle on the separation performance of a cyclone [J]. Chemical Engineering Research Design, 2009, 87: 1567-1572.

[30] TANG B, XU Y X, SONG X F, SUN Z, YU J G. Numerical study on the relationship between high sharpness and configurations of the vortex finder of a hydrocyclone by central composite design [J]. Chemical Engineering Journal, 2015, 278: 504-516.

[31] XU Y X, SONG X F, SUN Z, LU G M, LI P, YU J G. Simulation analysis of multiphase flow and performance of hydrocyclones at different atmospheric pressures [J]. Industrial & Engineering Chemistry Research, 2012, 51: 443-453.

[32] WANG B, YU A B. Numerical study of particle-fluid flow in hydrocyclones with different body dimensions [J]. Mineral Engineering, 2006, 19: 1022-1033.

[33] YANG Q, LV W J, MA L, WANG H L. CFD study on separation enhancement of mini-hydrocyclone by particulate arrangement [J]. Separation Purification Technology, 2013, 102: 15-25.

[34] HSIEH K T. Phenomenological model of the hydrocyclone [D]. Salt Lake City: The University of Utah, 1988.

[35] CHEN J W, HOU J W, LI G S, XU C Y, ZHENG B H. The effect of pressure parameters of a novel dynamic hydrocyclone on the separation efficiency and split ratio [J]. Separation Science Technology, 2015, 50: 781-787.

[36]  B, CONCHA F. Flow patterns in conical and cylindrical hydrocyclones [J]. Chemical Engineering Journal, 2000, 80: 267-273.

进口参数对旋流器分离性能的影响

唐 波，许妍霞，宋兴福，孙 泽，于建国

华东理工大学 国家盐湖资源综合利用工程技术研究中心，上海 200237

摘  要：进口参数是影响水力旋流器分级性能的重要因素，研究两者之间的影响规律具有重要意义。基于计算流体力学方法，以各种进口直径和进口速度的组合为研究对象，考察了进口参数对于精确分级的影响效应。结果显示：高分级精度的实现需要组合特定的进口直径和进口速度。过大的进口直径和过快的进口速度会降低分级精度。当进口直径过大时，由于短路流的显著影响，粗颗粒底流回收效率下降严重。流场分析发现原因是溢流管区域流体流动混乱程度的增加以及压力梯度的增强。与此同时，进口速度过快会导致细颗粒受到较大的离心力，引起溢流分离效率的降低。

关键词：水力旋流器；进口参数；分离精度；计算流体力学

(Edited by Yun-bin HE)

Foundation item: Project (2011AA06A107) supported by the National High Technology Research and Development Program of China; Project (2014M551348) supported by China Postdoctoral Science Foundation; Project (51504098) supported by the National Natural Science Foundation of China

Corresponding author: Xing-fu SONG; Tel: +86-21-64252170; E-mail: xfsong@ecust.edu.cn

DOI: 10.1016/S1003-6326(17)60187-0