矫直过程截面复杂反弯的应力分布与反弯特性解析
管奔1,臧勇1,逄晓男2,吕智勇2,曲为壮2
(1. 北京科技大学 机械工程学院,北京,100083;
2. 山东省莱芜钢铁股份有限公司型钢厂,山东 莱芜,271126)
摘要:为了深入研究和认识辊式矫直过程中截面的反弯特性,研究存在弹塑性弯曲历史的截面弯曲过程,采用工程弹塑性力学基本理论,建立合理的辊式矫直复杂弯曲力学模型。解析证明经历二次反弯的截面应力形式应当由两次弯曲参数构成的平面方能进行描述,二次反弯过程截面的弯矩(M)与曲率比(C)的关系实际为包含两次弯曲的2个弯曲参数的复杂函数。通过对经历二次反弯的截面应力分布与反弯特性的解析,证明辊式矫直过程中经历多次弹塑性弯曲的截面受变形历史的影响,其应力分布函数及M-C关系都不再是简单关系,而是包含全部弯曲历史参数的复杂函数形态。解析结果表明:辊式矫直过程中经历二次反弯的金属条材截面弹性极限弯矩值下降,弯曲所需弯矩减小,弯曲回弹比增大,工程应用时应对相关工艺参数进行相应调整。
关键词:辊式矫直;弹塑性;应力分析;弯矩-曲率;应力遗传
中图分类号:TG333.2 文献标志码:A 文章编号:1672-7207(2012)05-1739-07
Stress distribution and reverse bending behavior of section during roller leveling process
GUAN Ben1, ZANG Yong1, PANG Xiao-nan2, L? Zhi-yong2, QU Wei-zhuang2
(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Section Mill of Laiwu Iron & Steel Co. Ltd., Laiwu 271104, China)
Abstract:In order to study the bending behavior of the section during roller leveling process, the bending process of the section which contains the history of elastic-plastic bending process was investigated. With the basic theory of elastic-plastic mechanics, a reasonable mechanical model of complicated bending process of the section was built. With this model it is proved that the stress in the section coming from the second recurvate process must be described by the coordinate plane constituted by two bending parameters, and the M-C relation of the section coming from the second recurvate process is actually a complicated function which contains two bending parameters. By analyzing stress distribution and reverse bending behavior of the section coming from the second recurvate process, it is proved that the stress distribution and reverse bending behavior of the elastic-plastic bending section, affected by several times of deformation during roller leveling process, are no longer a simple one, but a complicated function which contains all the historical parameters of bending. Analytical results show that during the second recurvate process, there are decreased elastic limit bending moment, reduced bending moment and increased springback ratio. Therefore related parameters should be adjusted accordingly in terms of engineering application.
Key words:roller leveling; elastic-plastic; stress analysis; moment-curvature; stress heredity
弹塑性弯曲是一种重要的金属加工技术。在现代工业生产中,板条、型材和板的弹塑性弯曲被广泛地应用于大型金属结构及各种日常用品的制造过程[1],而在金属条材的生产过程中,作为最后一道塑性变形性质的辊式矫直工序更是典型的需要经历多次反弯的复杂弹塑性弯曲过程[2]。为设定辊式矫直过程合理的工艺参数及保证矫后条材的几何精度,需要对辊式矫直过程所特有的此类连续弹塑性反弯过程进行深入研究和准确认识。针对弹塑性弯曲,国内外学者进行了许多基于理论探索和工程应用的研究工作[3-5],大部分工作是以一次弯曲成型的金属塑性加工为应用背景,从而不存在考虑弯曲历史对截面特性的影响问题。实际上,金属条材的矫直是典型的多次弹塑性反弯的力学过程,矫直理论研究的力学基础却依然是基于不考虑截面弯曲历史的简单弹塑性弯曲理论,从而将截面各次反向弯曲作为没有关联的、各自独立的过程进行分析,因而造成理论分析与现场应用的较大差 距[2, 6-7]。使得对矫直过程现实问题的有效分析手段多为各种数值方法[8-14]。弹塑性弯曲是一种典型的截面不均匀变形状态,会使截面产生宏观残余应力[15],所以辊式矫直过程中截面多次弹塑性反弯是一个不断产生新的残余应力而同时截面应力又在不断进行重分布的演变过程,在此过程中前次弯曲产生的残余应力遗传至下一弯曲过程又必将会对下一弯曲过程的反弯特性产生影响。所以,在金属条材弹塑性连续反弯过程中存在一种截面弯曲特性与应力分布相耦合的演变过程,这时经典弹塑性弯曲理论已经不再适用,弯曲参数与力学参数间简单的函数关系也将不复存在。因此,要建立合理的辊式矫直过程弯曲力学模型、精确分析多次反弯的截面弯曲特性,必须建立考虑遗传变形历史的截面弹塑性弯曲理论。本文作者以无量纲化的矩形截面为例,基于弹塑性弯曲的基本理论,建立考虑截面反弯特性与应力遗传关系的弹塑性二次反弯过程力学模型体系,并对弯曲历史对截面应力分布及弯曲特性的影响进行研究,在此基础上,揭示辊式矫直过程截面弯曲特性的复杂函数关系,并对进一步的辊式矫直过程截面更多次反弯的参数关系解析函数形式进行论述。
1 矩形截面的弯曲特性
设矩形截面宽度为B,高度为H,弹性极限弯矩为Mt,弹性极限曲率角为At。弯曲时,截面弹性区高度为Ht,截面弯矩为M。
对矩形截面定义如下4个参数:
塑弯比 ,反映截面弯矩的大小;
,反映截面弯矩的大小;
弹区比 ,反映截面塑性变形程度;
,反映截面塑性变形程度;
曲率比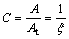 ,即弯曲过程中各种曲率角对弹性极限曲率角的比值,反映截面弯曲程度;
,即弯曲过程中各种曲率角对弹性极限曲率角的比值,反映截面弯曲程度;
相对高度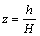 ,反映研究点的相对位置。
,反映研究点的相对位置。
由此,则实现了整个弯曲过程曲率、弯矩等各关系的无量纲化,无量纲参数 ,C和
,C和 是截面不同参数相对其弹性极限状态的比值。由截面高度为±1的无量纲化的矩形截面推导产生的各种关系适用于任何理想金属的矩形截面。
是截面不同参数相对其弹性极限状态的比值。由截面高度为±1的无量纲化的矩形截面推导产生的各种关系适用于任何理想金属的矩形截面。
2 弯曲应力与反弯特性耦合解析
2.1 简单弹塑性弯曲
若完全不考虑(或不存在)截面的弹塑性弯曲历程及由其产生的残余应力,则在此状态下进行的弹塑性弯曲可定义为简单弹塑性弯曲过程。而金属条材的辊式矫直截面第一次弯曲过程即属于此简单弹塑性弯曲状态。
经典的弹塑性弯曲理论中弹塑性弯曲和弹复过程如图1所示,其截面应力分布可分为加载应力和卸载后残余应力2种状态[16]。设截面屈服极限为σs,弯曲曲率比为C,则沿矩形截面高度z方向弯曲加载过程应力分布方程为
 (1)
(1)
对应力分布方程进行积分,得弯矩与曲率比的关系(即M-C关系)为
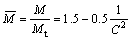 (2)
(2)
卸载后截面弯曲残余应力分布方程为
 (3)
(3)
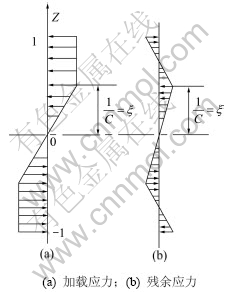
图1 简单弹塑性弯曲截面应力演变过程
Fig.1 Evolution of section stress during simple elastic-plastic bending process
2.2 二次弹塑性反弯
复杂弹塑性弯曲即是弯曲截面在简单弹塑性弯曲基础上,再经过了一次或多次弹塑性弯曲的过程。在复杂弹塑性弯曲过程中,由于残余应力的存在和作用,截面的变形历史开始影响弯曲过程中的曲率比与弯矩的关系。以辊式矫直截面第2次反弯过程为例进行分析,其在力学模型上是最简单的2次反弯过程,设截面第1次正向弯曲曲率比为CI,第2次反向弯曲曲率比为CII,现分析其第二次弯曲过程。
2.2.1 应力分布
设第1次弯曲截面残余应力为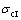 ,第2次弯曲过程产生的弯曲应力为
,第2次弯曲过程产生的弯曲应力为 ,根据弯曲过程变形的几何协调性和残余应力的叠加性,若不考虑应力的屈服条件,其理论弯曲应力的基本方程应为
,根据弯曲过程变形的几何协调性和残余应力的叠加性,若不考虑应力的屈服条件,其理论弯曲应力的基本方程应为
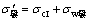
第2次弯曲单独形成有应力在弹性变形区应满足下式:
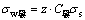 (4)
(4)
残余应力则满足式(3)。
设ξII为截面二次弯曲后的弹塑性分界点,应力 满足:
 (5)
(5)
在ξII以外为塑性区应力应直接取为 。
。
由式(5)可以确定ξII的位置。不过,由式(3)和图1(b)的复杂性可知:ξII和ξI的相对位置(前后二次的弯曲曲率比)不同,截面的应力分布不同,具体如图2所示,所以式(5)所确定的ξII的具体公式也不一样。
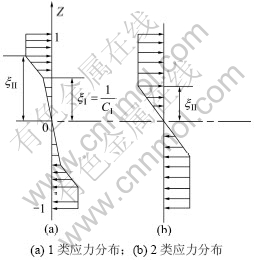
图2 复杂弹塑性弯曲加载过程应力分布情况
Fig.2 Distribution of section stress during loading step of complicated elastic-plastic bending process
(1) ξII>ξI。当后一次弯曲程度相对较低,加载后不能统一前一次弯曲造成的残余应力叠加效应时,截面应力分布如图2(a)所示,称为1类应力分布方式。
将式(3)及式(4)带入式(5)可得:

整理得弹区比ξⅡ:
 (6)
(6)
在考虑截面应力屈服条件的情况下,此时的截面加载后应力分布方程如下:
 (7)
(7)
利用静力平衡关系直接对截面应力分布方程积分求得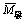 :
:

将式(7)带入上式并整理得复杂弹塑性弯曲过程的1类弯矩与曲率比关系方程(即M-C关系)如下:
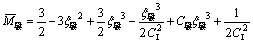 (8)
(8)
(2) ξII<ξI。当后一次弯曲程度相对较高,加载后完全消除前一次弯曲造成的残余应力效应时,截面应力分布如图2(b)所示,称为第2类应力分布方式。与第1类应力分布推导相同,可以获得:
 (9)
(9)
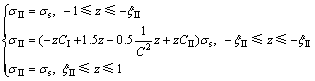 (10)
(10)
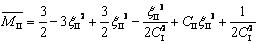 (11)
(11)
2.2.2 应力分布形式判别
由以上推导可知:复杂弯曲加载过程的应力分布形式与CI和CII的组合关系有关。为求得应力分布方式的判定方法,可取两分布方程都适用的边界情况,则:
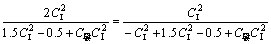
整理得两类应力分布边界函数为:
 (12)
(12)
实际上,式(12)就是ξII=ξI的关系式。
另外,除上述的弹塑性变形外,第二次弯曲也有可能存在弹性变形的情况。其极限情况是仅在边部出现塑性应力。此时由式(6)确定的ξII应落在边部,即为1。相应的弯曲曲率比即为复杂弹塑性弯曲状态下截面的弹性极限弯曲曲率比,即
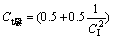 (13)
(13)
由式(13)可以看出:复杂弹塑性弯曲状态下,截面弹性极限弯曲曲率比CtII已经不再等于1,而是CI的函数,即与截面的变形历史有关。正常情况下, CI>1,因此CtII<1,即需要较小的力矩即可使断面产生塑性变形。
将式(12)和式(13)表示的曲线画在(CI,CII)平面上,可以得到复杂弹塑性弯曲过程的应力状态分布情况(图3)。上述2条曲线将平面分为弹性变形、1类应力和2类应力3个区域,具体情况则与CI和CII 2个参数的搭配相关,即复杂弹塑性弯曲的应力分布由2个弯曲参数共同决定。
由此可见:在辊式矫直截面二次反弯过程中,代表截面弯曲历史的参数CI对后次弯曲存在遗传影响作用,不考虑截面变形历史的弹塑性弯曲理论已经无法精确描述截面的弯曲性质。
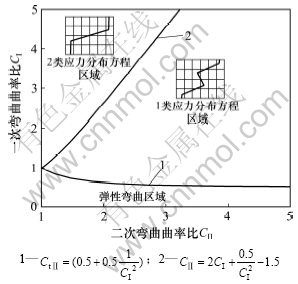
图3 复杂弯曲过程在(CI,CII )平面上的应力分布
Fig.3 Variation of stress distribution with bending parameter combination (CI, CII)
2.3 高次复杂弹塑性弯曲
在辊式矫直的实际过程中,金属条材各截面最终都将经历3次以上的弹塑性连续反弯过程。由以上二次反弯的弹塑性解析可知:随着截面反弯次数的不断增多,其应力遗传耦合关系将会越来越复杂。
通过对二次反弯的推导,可以对更高次的复杂弹塑性弯曲的截面弯曲特性函数进行如下描述:若设辊式矫直过程截面经历n次弯曲,则其截面变形历史将由CI,CII,…,Cn共 n个弯曲参数进行定义,其应力分布方程可能是一个n元2n+1段的分段函数,其应力分布特征需采用n维空间方可进行描述。
可见:采用解析方法对辊式矫直高次的复杂弹塑性弯曲过程进行彻底的解析较为困难,有赖于采用合理的数值方法进行分析。
3 二次反弯过程的弯曲特性分析
3.1 加载过程M-C曲线
加载过程中的M-C曲线集中反映着弹塑性弯曲加载过程截面的弯曲特性,对于实际工程应用中合理地设定弯曲参数具有重要指导意义。
由以上理论公式(8)和(11)可以得到二次反弯加载过程中弯曲特性(即M-C曲线),如图4所示。
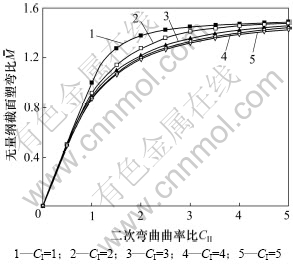
图4 二次反弯过程M-C曲线
Fig.4 M-C curves during the second reverse bending process
由图4的M-C曲线可以看出:CI=1时,前次弯曲并没有进入弹塑性弯曲状态,二次反弯过程的M-C曲线与简单弹塑性弯曲过程相同。对比CI=1的曲线,前次简单弯曲若进入弹塑性弯曲状态,则二次反弯过程截面弹性极限弯矩将按照式(13)的规律减小,相同曲率比条件下截面所需弯矩更小,即截面更易于发生弹塑性弯曲。同时,随着前次弯曲曲率比的增大,截面二次反弯弯矩减小的趋势将放缓。而M-C关系在整个(CI,CII)平面上的曲面及等值线投影见图5。
由以上对复杂反弯加载过程进行的分析可以发现,经历二次反弯的截面更易于进行弯曲。这也就是说,在实际辊式矫直的弹塑性弯曲过程中,矫直机第3辊(即截面第2次弯曲位置)相较于经典理论应减小弯矩水平,即适当减小压下量,才能达到截面理想的弯曲曲率要求。
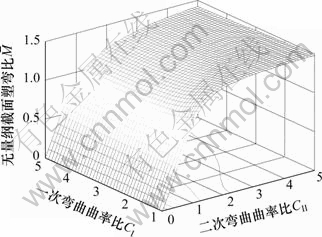
图5 二次反弯过程M-C关系在(CI,CII)平面上的曲面
Fig.5 M-C relation surface on (CI, CII) coordinate plane during the second reverse bending process
3.2 卸载过程应力分布及回弹特性
根据弹塑性理论,截面弹塑性弯曲的卸载过程相当于叠加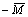 引起的纯弹性效应[7]。因此,回弹后的残余应力
引起的纯弹性效应[7]。因此,回弹后的残余应力 分布符合下式:
分布符合下式:
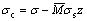
由于二次反弯加载弹复后应力分布函数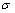 及M-C关系函数极为复杂,因此不再列出完整的二次反弯残余应力分布函数。
及M-C关系函数极为复杂,因此不再列出完整的二次反弯残余应力分布函数。
以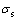 =235 MPa为例,当CII=3时,卸载后截面的残余应力分布状态随CI的变化如图6所示。由图6可以看出:前次弹塑性弯曲历史对截面中心部位的残余应力分布形式具有很大的影响,而在连续反弯过程中截面边部的残余应力水平则与本次反弯参数相关较大,边部残余应力处在不断变化的状态,对经历辊式矫直过程多次弯曲的截面残余应力状态的分析有赖于其整个变形历史的弯曲参数。
=235 MPa为例,当CII=3时,卸载后截面的残余应力分布状态随CI的变化如图6所示。由图6可以看出:前次弹塑性弯曲历史对截面中心部位的残余应力分布形式具有很大的影响,而在连续反弯过程中截面边部的残余应力水平则与本次反弯参数相关较大,边部残余应力处在不断变化的状态,对经历辊式矫直过程多次弯曲的截面残余应力状态的分析有赖于其整个变形历史的弯曲参数。
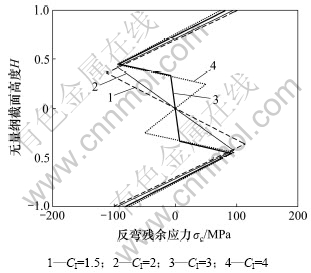
图6 CII=3的二次反弯卸载后截面残余应力分布
Fig.6 Distribution of section residual stress after unloading step of the second reverse bending process for CII=3
同样,由于弹复过程的纯弹性效应,弹复后截面曲率比Cf符合下式:
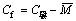
可以定义回弹比[1]: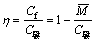
回弹比是考察截面回弹特性的重要参照量。该量在板条弯曲加工中用于判断截面是否能更好地保持受弯时的形状[1]。在辊式矫直过程中也是对条材残留曲率比计算的重要指标。二次反弯过程中回弹比随前次弯曲参数的变化如图7所示。
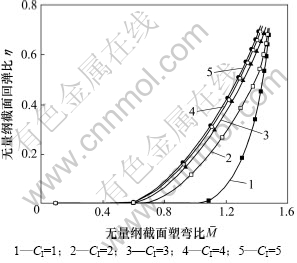
图7 二次反弯回弹比曲线
Fig.7 Springback ratio curve during the second reverse bending process
由图7可以看出:前次弯曲历史的存在会使得回弹比增大,而且随着前次弯曲曲率比的增大回弹比也呈增大趋势,即弯曲曲率比CII与弹复后曲率比Cf更加接近。这就说明经历二次反弯的截面卸载时能更好地保持受弯时的形状。因此对于辊式矫直过程而言,经历前次弯曲的金属条材在矫直机第3辊的2次反弯过程中需要相对于经典公式减小压下量以利于其残余曲率比的控制。
4 结论
(1) 理论解析证明辊式矫直多次弹塑性反弯过程中截面存在着与反弯历史相关的、复杂的应力分布与反弯特性关系。
(2) 复杂弹塑性弯曲的弯曲特性参数均是包含截面整个弯曲历史参数的复杂函数。
(3) 辊式矫直过程经历二次反弯的条材截面弹性极限弯矩减小,截面更易于弯曲。
(4) 辊式矫直过程经历复杂反弯的截面残余应力状态有赖于其整个变形历史的弯曲参数。
(5) 经历二次反弯的截面回弹比增大,截面能更好地保持受弯时的形状,应有针对性地相对于经典公式减小压下量,控制残余曲率比。
参考文献:
[1] 余同希, 章亮炽. 塑性弯曲理论及其应用[M]. 北京: 科学出版社, 1992: 2-126.
YU Tong-xi, ZHANG Liang-chi. Plastic bending theory and its application[M]. Beijing: Science Press, 1992: 2-126.
[2] 崔甫. 矫直原理与矫直机械[M]. 2版. 北京: 冶金工业出版社, 2002: 157.
CUI Fu. Straightening and straightening machine[M]. 2nd ed. Beijing: Metallurgical Industry Press, 2002: 157.
[3] Yu T X, Johnson W. Influence of axial force on the elastic-plastic bending and springback of a beam[J]. Journal of Mechanical Working Technology, 1981(6): 5-12.
[4] Schleinzer G, Fischer F D. Residual stress formation during the roller straightening of railway rails[J]. International Journal of Mechanical Sciences, 2001, 43: 2281-2295.
[5] Johnson W, Yu T X. On the range of applicability of results for the springback of an elastic/perfectly plastic rectangular plate after subjecting it to biaxial pure bending[J]. Int J Mech Sci, 1981, 23: 631-637.
[6] 臧勇, 王会刚, 崔福龙. 型钢辊式矫直压弯挠度的弹塑性解析[J]. 机械工程学报, 2005, 41(11): 47-51.
ZANG Yong, WANG Hui-gang, CUI Fu-long. elastic-plastic analyses of bending deflection on section roller straightening[J]. Chinese Journal of Mechanical Engineering, 2005, 41(11): 47-51.
[7] 周存龙, 王国栋, 谢东钢, 等. 辊式矫直过程中板带弯曲挠度的确定[J]. 太原科技大学学报, 2009, 30(1): 48-50.
ZHOU Cun-long, WANG Guo-dong, XIE Dong-gang, et al. Effect of entrance/exit leveler roller intermesh to plate flatness[J]. Journal of Taiyuan University of Science and Technology, 2009, 30(1): 48-50.
[8] 薛军安, 崔丽, 胡贤磊, 等. 辊式矫直过程的接触倾角与曲率耦合分析[J]. 中国冶金, 2009, 19(2): 23-26.
XUE Jun-an, CUI Li, HU Xian-lei, et al. Analysis of contact angle and curvature during roller leveling process[J]. China Metallurgy, 2009, 19(2): 23-26.
[9] 周剑华, 吴迪, 赵宪明, 等. 辊式水平矫直对重轨断面尺寸的影响分析[J]. 钢铁, 2009, 44(2): 40-43.
ZHOU Jian-hua, WU Di, ZHAO Xian-ming, et al. Effect of horizontal roll straightening on cross section dimensions of heavy rail[J]. Iron & Steel, 2009, 44(2): 40-43.
[10] 崔丽红, 臧勇, 章博, 等. 多辊矫直过程中H型钢断面的应力演变规律[J]. 北京科技大学学报, 2008, 30(8): 942-946.
CUI Li-hong, ZANG Yong, ZHANG Bo, et al. Stress evolvement rule of an H-beam section during multi-roller straightening process[J]. Journal of University of Science and Technology Beijing, 2008, 30(8): 942-946.
[11] 周文, 刘学毅. 高速道岔尖轨矫直的有限元分析[J]. 西南交通大学学报, 2008, 43(1): 82-95.
ZHOU Wen,LIU Xue-yi. FEM simulation of straightening tongue rail of high-speed turnout[J]. Journal of Southwest Jiaotong University, 2008, 43(1): 82-95.
[12] 王福华, 刘安中, 李友荣,等. 辊式矫直机上辊压下规程的仿真分析[J]. 武汉科技大学学报, 2009, 32(4): 351-354.
WANG Fu-hua,LIU An-zhong, LI You-rong,et al. Simulation analysis of upper rolling schedule of roll-type straightener[J]. Journal of Wuhan University of Science and Technology, 2009, 32(4): 351-354.
[13] 高燕, 臧勇. 辊式矫直中H型钢断面畸变的仿真分析[J]. 北京科技大学学报, 2006, 28(12): 1157-1161.
GAO Yan, ZANG Yong. Finite element simulation of section deflection during H-beam roller straightening[J]. Journal of University of Science and Technology Beijing, 2006, 28(12): 1157-1161.
[14] 王会刚, 刘学江,刘炳新,等. 有限差分法在H型钢辊式矫直压下挠度计算中的应用[J]. 锻压技术, 2005(6): 41-43.
WANG Hui-gang,LIU Xue-jiang,LIU Bing-xin,et al. Application of finite difference calculus in bending deflection calculation of H-beam roller straightenning[J]. Forging & Stamping Technology, 2005(6): 41-43.
[15] 米谷茂. 残余应力的产生和对策[M]. 朱荆璞, 邵会孟, 译. 北京: 机械工业出版社, 1983: 10.
Yonetani Shigeru. The engender theory and countermeasure of residual stress[M]. ZHU Jing-pu, SHAO Hui-meng, transl. Beijing: China Machine Press, 1983: 10.
[16] 徐秉业, 刘信声. 应用弹塑性力学[M]. 北京: 清华大学出版社, 1995: 50-51.
XU Bing-ye, LIU Xin-sheng. Applied elastic-plastic mechanics[M]. Beijing: Tsinghua University Press, 1995: 50-51.
(编辑 杨幼平)
收稿日期:2011-06-29;修回日期:2011-09-14
基金项目:国家高技术研究发展计划(“863”计划)项目(2009AA03Z515);国家自然科学基金资助项目(50775010)
通信作者:臧勇(1963-),男,江苏铜山人,教授,博士生导师,从事塑性加工工艺研究;电话:010-62334441;E-mail: yzang@ustb.edu.cn