Trans. Nonferrous Met. Soc. China 26(2016) 2724-2730

Three-dimensional orebody modelling and intellectualized longwall mining for stratiform bauxite deposits

Shao-feng WANG¹, Xi-bing LI¹, Shan-yong WANG², Qi-yue LI¹, Chong CHEN¹, Fan FENG¹, Ying CHEN¹

1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. ARC Centre of Excellence for Geotechnical Science and Engineering, The University of Newcastle Callaghan, NSW 2308, Australia

Received 14 January 2016; accepted 12 June 2016

Abstract: A coupled biharmonic spline and linear interpolation algorithm was proposed to create a three-dimensional smooth deposit model with minimal curvature containing grade and position data. To obtain the optimal technical parameters, such as cutting height and drum diameter, a virtual longwall mining procedure was modelled by simulating the actual fully mechanized longwall mining process. Based on the above work, a bauxite deposit in a longwall mining panel was modelled by scattered grade data from ores sampled on the entry wall. The deposit was then demarcated by industrial indexes and sliced according to the virtual longwall mining procedure. The results show that the proposed interpolation algorithm can depict the stratiform structure of bauxite deposits and that the uncovered bauxite deposit has high proportions of high-grade and rich ore. The ranges of optimal cutting height and drum diameters are 1.72-2.84 m and 1.42-1.72 m, respectively. Finally, an intellectualized longwall mining procedure was designed to guide the mining process with the lowest dilution and loss rates.

Key words: stratiform bauxite deposit; orebody modelling; interpolation algorithm; virtual longwall mining; cutting height; drum diameter

1 Introduction

Bauxite is a naturally occurring mixture composed of hydrated aluminum oxides, Si oxide, Fe oxides and other compounds [1,2]. The mass fraction of Al oxide and the mass ratio of Al oxide to Si oxide are the two important industrial indexes that determine the industrial value and availability of bauxite [3]. Bauxite resources are mainly distributed in Guinea, Australia, Brazil, Venezuela, Jamaica, India and China [4]. In 2013, the aluminum consumption of China reached 25.5 million tons due to rapid economic development, which is the largest and the fastest-growing consumption rate in the world [5]. This consumption rate requires a large supply of bauxite. However, relative to coal mining, bauxite mining technology is still underdeveloped and is mainly dominated by the traditional drilling and blasting methods, resulting in the high dilution and loss rates. In addition, with the depletion of bauxite resources in shallow ground and the increasing demand for aluminum products, large-scale mining for underground bauxite has become an inevitable trend.

Longwall mining is a widely used method for mechanized continuous and large-scale extraction of underground coal [6-9], which is a feasible technique for achieving the automated, unmanned, and even intellectualized exploitation of underground mineral resources. However, further application of fully mechanized longwall mining for nonferrous metal deposits is still rare. In general, for underground stratiform bauxite deposits composed of bauxite and bauxitic rock, the natural uniaxial compressive strength is generally lower than 30 MPa, which is the applicative and economical cutting strength of a shearer [8]. Additionally, the occurrence of stratiform bauxite deposits is usually uncomplicated and has good continuity. Therefore, the application of longwall mining for stratiform bauxite deposits is feasible. However, the specific technical parameters, such as cutting height and drum diameter, need to be further investigated.

Accurate description of the shape, location, size, inclination and grade of an orebody is essential for the optimization, evaluation and design of technical parameters of longwall mining. Therefore, orebody modelling is a fundamental task [10]. It is frequently the case, however, that available data are sparse and scattered, and no data are available from positions between over-sampled locations [11]. Hence, there is often a need to estimate values for locations where there are no measurements by interpolation techniques selected according to either statistical or deterministic criteria [12]. Among statistical methods, geostatistical kriging-based techniques have often been used for spatial analysis [13-16]. For deterministic methods, inverse distance weighted interpolation, the nearest neighbor method, bicubic functions, non-uniform rational B-splines and other methods are often applied [17-19]. In addition, artificial neural network [20], fuzzy methodology [21], evolutionary algorithm [22], support vector machine [23] and fractal interpolation algorithms [24] have also been applied to orebody modelling and grade estimation. However, the methods mentioned above were less satisfactory in depicting the thin and anfractuous stratiform deposit, and it is difficult to achieve smooth interpolation from exceedingly discrete data.

In this work, the coupled biharmonic spline and linear interpolation algorithm was proposed for depicting the three-dimensional grade distribution of stratiform bauxite deposits. Based on a bauxite deposit model containing grade distribution information, the orebody in the 1102 panel in Wachangping Bauxite Mine was demarcated by industrial indexes of bauxite. Furthermore, a virtual longwall mining algorithm and a comprehensive evaluation function composed of dilution and loss rates were used to obtain the optimal cutting height and drum diameter of the shearer for conducting intellectualized mining.

2 Methodology

For underground stratiform bauxite deposits, an accurate deposit model containing position and grade data is a necessary precondition for the feasible analysis and parameter design of fully mechanized longwall mining. The bauxite deposit modelling and intellectualized longwall mining procedure is shown in Fig. 1. The key steps of this process are the bauxite deposit modelling by coupled biharmonic spline and linear interpolation and cutting height optimization by virtual longwall mining.

2.1 Bauxite deposit modelling

2.1.1 Biharmonic spline interpolation

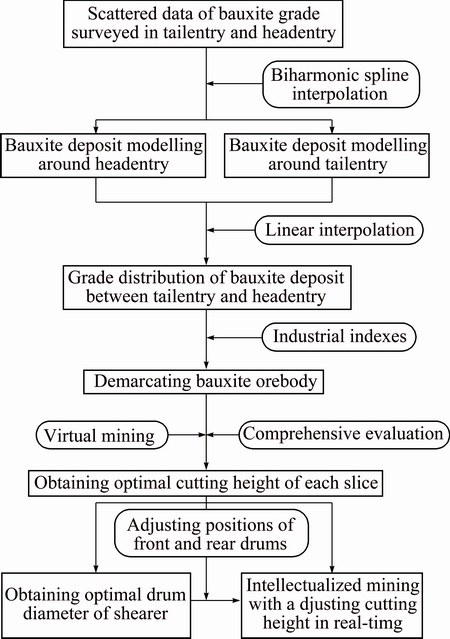
Fig. 1 Flowchart of bauxite deposit modelling and intellectualized longwall mining

Biharmonic spline interpolation is used for minimum curvature interpolation and for finding the smoothest surface or curve passing through irregularly spaced and scattered data points. It is more accurate than other methods because the interpolating curve or surface, which is a linear combination of Green functions centered at each data point, satisfies the biharmonic equation and therefore has the minimum curvature [25,26].

Biharmonic spline interpolation is used to find a biharmonic function that passes through N data points. For N data points in m-dimensions, the function for the spline satisfies the biharmonic equation:

                (1)

                             (2)

where is the biharmonic operator, x is a position in the m-dimensional space, w(x) is a biharmonic function that passes through N data points w_i located at x_i, k_j is an undetermined coefficient, and δ is the Dirac Delta function [26].

In one dimension,

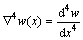                                               (3)

                                       (4)

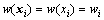                                          (5)

In two dimensions,

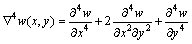              (6)

                    (7)

                         (8)

The general solution to Eq. (1) is

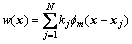                      (9)

The undetermined coefficient k_j is solved by the following linear system:

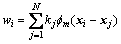                        (10)

where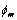 is a Green function.

In one dimension,

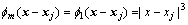              (11)

In two dimensions,

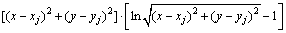  (12)

2.1.2 Grade distribution model

The coupled biharmonic spline and linear interpolation algorithm was proposed to achieve a three-dimensional distribution model of bauxite grade. As shown in Fig. 2, the two-dimensional grade distributions along the headentry and tailentry walls of a longwall mining panel can be realized by the above biharmonic spline interpolation algorithm. Then, based on the linear interpolation algorithm, the bauxite grade in positions between headentry and tailentry can be estimated.

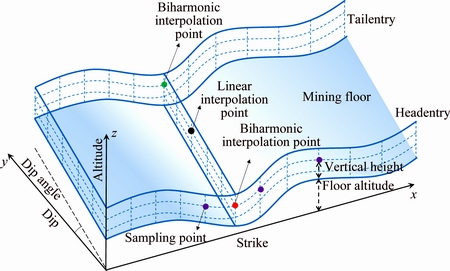
Fig. 2 Schematic diagram of three-dimensional coordinates and interpolation procedure

According to Fig. 2, which shows the coordinate system and interpolation procedure, the modelling processes of a three-dimensional grade distribution model are as follows:

Firstly, according to the two-dimensional biharmonic spline interpolation, the bauxite grade distribution in positions on the entry wall relative to the headentry or tailentry floor can be given as

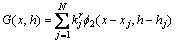                (13)

where G(x, h) is the grade distribution along entry wall relative to floor, h is the vertical height of a position from entry floor, and 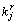 is the interpolation coefficient solved by the linear system shown in Eq. (10).

Secondly, based on the one-dimensional biharmonic spline interpolation, the headentry or tailentry floor curve can be expressed as

                       (14)

where z_b is entry floor altitude, and 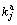is the interpolation coefficient.

Then, the bauxite grade distribution along the entry wall can be represented as

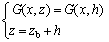                         (15)

Finally, the linear interpolation algorithm can be used to achieve the bauxite grade distribution between headentry and tailentry. It can be written as

               (16)

where G(x, y, z), G_h(x_h, z_h) and G_t(x_t, z_t) are the grade distributions between headentry and tailentry wall, along headentry wall and along tailentry wall, respectively, and (x_h, y_h, z_h) and (x_t, y_t, z_t) are a pair of positions on headentry and tailentry walls, respectively.

2.1.3 Orebody demarcating

Subjected to the current technological levels of mineral separation and metallurgy, the grade of bauxite should meet several indexes to be used in industrial processing and manufacturing. According to these industrial indexes, a bauxite orebody can be demarcated as

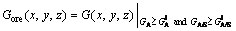      (17)

where G_ore(x, y, z) is the orebody demarcated by industrial indexes, G_A and 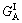 are the mass fraction distribution and industrial indexes of Al oxide, respectively, and G_A/S and  are the distribution and industrial indexes of the mass ratio of Al oxide to Si oxide, respectively.

2.2 Virtual longwall mining

The bauxite seam cut by the shearer in a longwall panel is extracted slice by slice. The cutting height of the shearer is a key technical parameter of fully mechanized longwall mining that determines the ore dilution rate and loss rate. Cutting height can be adjusted by the ranging arms, which are used to alter the size of the overlapping zone between the two cutting drums mounted on the front and rear of the shearer. The adjustable range of cutting height is from single to double the diameter of the cutting drum. The virtual longwall mining procedure for bauxite deposits is shown in Fig. 3, and the details of which are as follows:

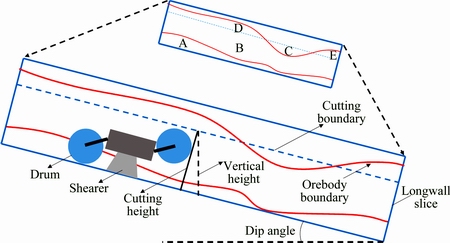
Fig. 3 Virtual longwall mining process of longwall slice

1) Giving a cutting height, H_ij, of the jth cutting height in the ith cutting step or longwall slice of 0.8 m in thickness;

2) Calculating the volumes of the mined and residual ores;

3) Calculating the average grades of the mined ore and ore-rock;

4) Calculating the dilution and loss rates with the following expressions:

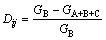                         (18)

                 (19)

where D_ij and L_ij are the dilution and loss rates, respectively; G_B and G_A+B+C are the average grades of mined ore and ore-rock, respectively; and V_B, V_B+D+E, V_D+E are the volumes of mined, total and residual ore, respectively;

5) Obtaining the optimal cutting height, 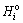, when the following expression composed of dilution and loss rates reaches its minimum value;

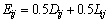                          (20)

6) For the (i+1)th cutting step, repeating the above procedures to achieve the optimal cutting height ;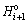

7) Repeating the above steps to obtain the optimal cutting height for each longwall slice.

3 Sampling data

The chemical components of bauxite or bauxitic rock were measured in 53 groups of samples obtained from entry-exploring grooves, including 27 groups from the tailentry and 26 groups from the headentry. Furthermore, the mass fraction of Al oxide w(Al₂O₃) and the mass ratio of Al oxide to Si oxide w(Al₂O₃)/w(SiO₂) were achieved and are depicted in Fig. 4.

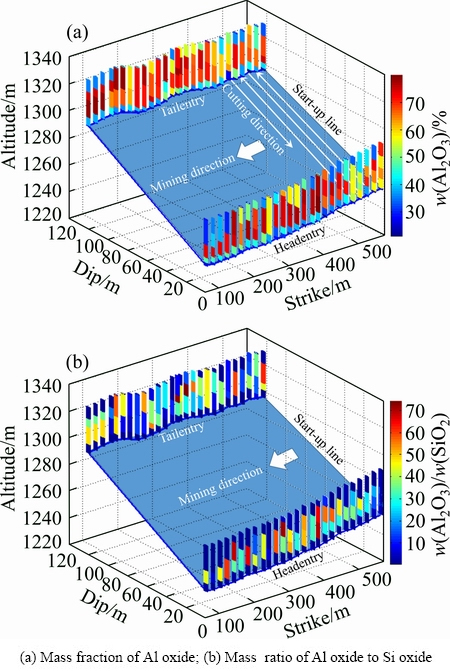
Fig. 4 Scattered grade and location data of sampling points in headentry and tailentry

4 Results and discussion

4.1 Bauxite deposit modelling

According to Eqs. (13)-(16), the three-dimensional grade distribution of stratiform bauxite deposit was modelled with sampling data, as shown in Fig. 4. Slice maps of grade distribution along sections parallel to the entry wall are shown in Figs. 5 and 6.

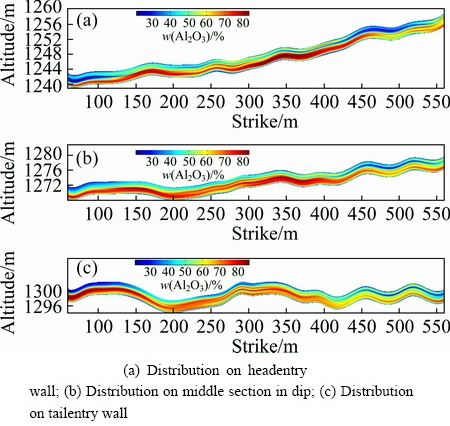
Fig. 5 Slice maps of Al oxide mass fraction distribution along sections parallel to entry wall

Fig. 6 Slice maps of mass ratio distribution of Al oxide to Si oxide along sections parallel to entry wall

It is evident that the grade distribution model is able to describe the stratiform occurrence of bauxite deposits, and the constructed deposit model is very smooth and has minimum curvature. The total volume of the bauxite deposit in the longwall mining panel at the headentry, tailentry and start-up line is 1.89×10⁵ m³. Additionally, the average values of w(Al₂O₃) and w(Al₂O₃)/w(SiO₂) are 56.34% and 16.88, respectively. These values meet the industrial indexes of w(Al₂O₃)≥55% and w(AL₂O₃)/ w(SiO₂)≥3.5. Therefore, this bauxite deposit has high exploitation value.

4.2 Orebody

Based on Eq. (17) and the industrial standards, a bauxite orebody in a longwall mining panel was demarcated. Slice maps of this orebody are shown in Fig. 7. The total volume of the bauxite orebody in this longwall mining panel is 9.94×10⁴ m³, and the average values of w(Al₂O₃) and w(Al₂O₃)/w(SiO₂) are 62.82% and 26.96, respectively. These values are much larger than the lower limits of the industrial indexes. This means that a large proportion of the orebody is rich in bauxite.

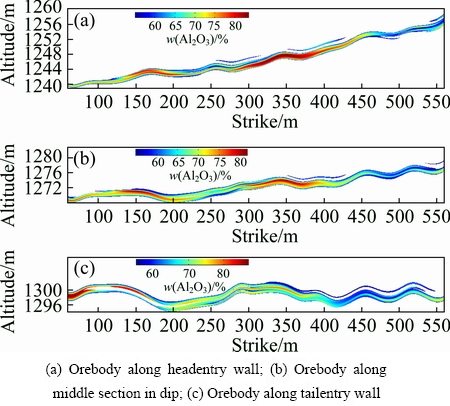
Fig. 7 Slice maps of orebody along sections parallel to entry walls

4.3 Cutting height and drum diameter

In accordance with the virtual longwall mining procedures, the optimal cutting height in each longwall slice was obtained. Based on a comprehensive evaluation function shown in Eq. (20) with a loss rate and dilution rate of approximately w(Al₂O₃) and a loss rate and dilution rate of approximately w(Al₂O₃)/w(SiO₂), the change curves of the optimal cutting heights along the mining direction (or deposit strike) are calculated and depicted in Fig. 8. This figure shows that the optimal cutting heights vary from 1.72 m to 2.84 m. Therefore, the suitable diameter range of the cutting drum of the shearer is from 1.42 m to 1.72 m. Corresponding to these values of drum diameter, the cutting range of the shearer is between 1.42 m and 3.44 m and therefore meets all the optimal cutting heights throughout the mining direction.

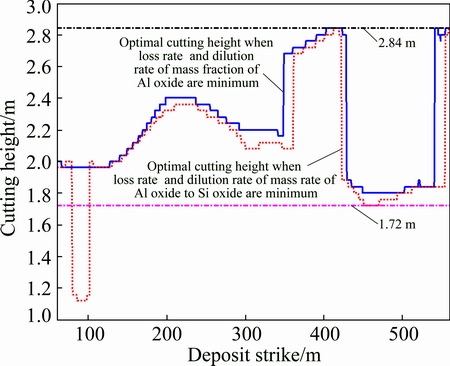
Fig. 8 Change curves of optimal cutting heights along deposit strike

4.4 Intellectualized longwall mining

The procedures of the intellectualized longwall mining are as follows:

1) Outputting the optimal cutting height, 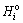, about the ith longwall slice, which is contained in the orebody model and obtained by the virtual longwall mining model mentioned above;

2) Transmitting cutting height to adjuster;

3) Transforming cutting height into a parameter of overlapping thickness, D_i, used to adjust the position of the cutting drums, the process of which is expressed as

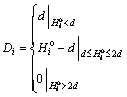                      (21)

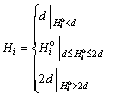                        (22)

where d is the diameter of the cutting drum, and H_i is the cutting height of the shearer;

4) Transmitting the adjusting parameter to the shearer, which then automatically adjusts the cutting position of the drums by the ranging arms;

5) Cutting the orebody by the reciprocating motion of the shearer, slice by slice, along the cutting direction. In a round trip, the shearer will move forward by two cutting steps along the mining direction;

6) Continuously cutting the orebody from the start-up line to the stopping line following the above processes.

5 Conclusions

1) A three-dimensional grade distribution model of the mass fraction of Al oxide and the mass ratio of Al oxide to Si oxide in stratiform bauxite deposits was developed using a coupled biharmonic spline and linear interpolation algorithm. Based on this model, the orebody of the 1102 longwall mining panel in Wachangping Bauxite Mine was modelled with sampling data measured from the entry walls and demarcated by industrial indexes of bauxite. Furthermore, a virtual longwall mining procedure was proposed to achieve the optimal cutting height and drum diameter of the shearer for conducting intellectualized mining.

2) The coupled biharmonic spline and linear interpolation algorithm can be used to model stratiform deposits with the thin and anfractuous occurrence features and scattered sampling data. Based on this algorithm, the three-dimensional bauxite deposit in the 1102 longwall mining panel was modelled with smooth connection and minimal curvature. The total volume of the bauxite deposit is 1.89×10⁵ m³, and the average values of w(Al₂O₃) and w(Al₂O₃)/w(SiO₂) are 56.34% and 16.88, respectively. The volume of the demarcated orebody is 9.94×10⁴ m³, and the average values of w(Al₂O₃) and w(Al₂O₃)/w(SiO₂) are 62.82% and 26.96, respectively. These results mean that the uncovered bauxite deposit is of high grade, and the rich ore is relatively concentrated.

3) Using the proposed virtual longwall mining procedure, the cutting of the bauxite deposit slice by slice can be simulated to determine the optimal technical parameters. For the bauxite deposit in the 1102 longwall mining panel, the optimal cutting heights vary from 1.72 m to 2.84 m, and the suitable drum diameter range is from 1.42 m to 1.72 m. Correspondingly, the cutting range of the shearer is between 1.42 m and 3.44 m, which meets all the optimal cutting heights throughout the mining direction.

Acknowledgments

The authors would like to thank Wachangping Bauxite Mine of China Power Investment Corporation, which supported the on-site data collection.

References

[1] MII (Mineral Information Institute). Aluminum & bauxite [EB/OL]. [2009]. http://www.mii.org/Minerals/photoal.html.

[2] MEYER F M. Availability of bauxite reserves [J]. Natural Resources Research, 2004, 13(3): 161-172.

[3] GB/T 24483-2009. Bauxite [S]. Beijing: Standards Press of China, 2009. (in Chinese)

[4] USGS (United States Geological Survey). Mineral commodity summaries: Bauxite and alumina. [EB/OL]. http://minerals.usgs.gov/ minerals/pubs/commodity/bauxite/index.html#mcs.

[5] LI C F, LIU Z J, WANG J P, MI K F, LIU R B. Current status and sustainable development of aluminum resources in China [J]. China Mining Magazine, 2014, 23(8): 5-10. (in Chinese)

[6] REZAEI M, HOSSAINI M F, MAJDI A. Determination of longwall mining-induced stress using the strain energy method [J]. Rock Mechanics and Rock Engineering, 2015, 48(6): 2421-2433.

[7] PENG S S. Coal mine ground control [M]. 3rd ed. Xuzhou: China University of Mining and Technology Press, 2013: 11-15. (in Chinese)

[8] PENG S S. Longwallmining [M]. 2nd ed. Englewood: Society for Mining, Metallurgy, and Exploration, Inc. (SME), 2006: 1-20.

[9] HU S S, LIU X Y, CHENG Y Q. Technical revolution in coal mining history, 40 years development of fully mechanized coal mining in China [J]. Journal of China Coal Society, 2010, 35(1): 1769-1771. (in Chinese)

[10] MORTENSEN M E. Geometric modeling [M]. New York: Wiley, 1985.

[11] CALCAGNO P,  J P, COURRIOUX G, GUILLEN A. Geological modelling from field data and geological knowledge. Part I: Modelling method coupling 3D potential-field interpolation and geological rules [J]. Physics of the Earth and Planetary Interiors, 2008, 171(1): 147-157.

[12] BASCETIN A, TUYLU S, NIETO A. Influence of the ore block model estimation on the determination of the mining cutoff grade policy for sustainable mine production [J]. Environmental Earth Sciences, 2011, 64(5): 1409-1418.

[13] JOURNEL A G. Geostatistics: Models and tools for the earth sciences [J]. Mathematical Geology, 1986, 18(1): 119-140.

[14] CRESSIE N A. Statistics for spatial data [M]. 1st ed. Ontario: Wiley, 1993.

[15] DEUTSCH C V. Geostatistical reservoir modeling [M]. New York: Oxford University Press, 2002.

[16] EDIGBUE P, OLOWOKERE M T, ADETOKUNBO P, JEGEDE E. Integration of sequence stratigraphy and geostatistics in 3-D reservoir modeling: A case study of otumara field, onshore niger delta [J]. Arabian Journal of Geosciences, 2015, 8(10): 8615-8631.

[17] FISHER T R, WALES R Q. Three-dimensional modelling of geo-objects using non-uniform rational B-splines (NURBS) [C]//Three-dimensional Modelling with Geoscientific Information Systems. Netherlands: Springer, 1992: 85-105.

[18] BABAK O, DEUTSCH C V. Statistical approach to inverse distance interpolation [J]. Stochastic Environmental Research & Risk Assessment, 2009, 23(5): 543-553.

[19] BABISH G. Geostatistics without tears: A practical guide to surface interpolation, geostatistics, variograms and kriging [M]. Gatineau: Environment Canada, 2006: 117.

[20] WANG Z H, CHEN Y X. 3D deposit model based on artificial neural network [J]. Journal of China Coal Society, 2005, 30(6): 730-732. (in Chinese)

[21] TUTMEZ B. An uncertainty oriented fuzzy methodology for grade estimation [J]. Computers & Geosciences, 2007, 33(2): 280-288.

[22] SAMANTA B, BANDOPADHYAY S. Construction of a radial basis function network using an evolutionary algorithm for grade estimation in a placer gold deposit [J]. Computers & Geosciences, 2009, 35(8): 1592-1602.

[23] SMIRNOFF A, BOISVERT E, PARADIS S J. Support vector machine for 3D modelling from sparse geological information of various origins [J]. Computers & Geosciences, 2008, 34(2): 127-143.

[24] HU N L, CHEN J J, LI G Q, YANG H. Application of a four-dimensional space fractal interpolation algorithm in grade estimation [J]. Chinese Journal of Engineering, 2015, 37(5): 556-560. (in Chinese)

[25] BRIGGS I C. Machine contouring using minimum curvature [J]. Geophysics, 1974, 39(1): 39-48.

[26] SANDWELL D T. Biharmonic spline interpolation of GEOS-3 and SEASAT altimeter data [J]. Geophysical Research Letters, 1987, 14(2): 139-142.

铝土矿层三维建模及智能化长壁开采

王少锋¹，李夕兵¹，王善勇²，李启月¹，陈 冲¹，冯 帆¹，陈 英¹

1. 中南大学 资源与安全工程学院，长沙 410083；

2. ARC Centre of Excellence for Geotechnical Science and Engineering,

The University of Newcastle Callaghan, NSW 2308, Australia

摘  要：联合采用Biharmonic样条插值和线性插值方法，构建含有位置坐标和品位数据的铝土矿层三维模型；模拟长壁开采实际过程，建立虚拟开采程序对矿层模型进行不同切割高度下的开采推演，基于矿石贫化率和损失率研究每个切割步骤的最佳切割高度以及合理的截割滚筒直径。结果表明，Biharmonic样条和线性耦合插值方法能够准确描述铝土矿层的层状结构，揭露的矿层品位高、富矿比例大、具有较高的开采价值，并且最佳的截割高度范围和截割滚筒直径范围分别为1.72~2.84 m和1.42~1.72 m。根据研究结果，构建能够智能化实时调节开采高度的控制程序，用于指导实际的长壁开采过程，并保证最小的矿石贫化率和损失率。

关键词：铝土矿层；矿体建模；插值算法；虚拟长壁开采；切割高度；滚筒直径

(Edited by Yun-bin HE)

Foundation item: Project (11472311) supported by the National Natural Science Foundation of China; Project (2015CX005) supported by the Innovation Driven Plan of Central South University of China; Project (2015zzts083) supported by the Fundamental Research Funds for the Central Universities of Central South University, China

Corresponding author: Xi-bing LI; Tel: +86-731-88877254; E-mail: xbli@csu.edu.cn

DOI: 10.1016/S1003-6326(16)64367-4