强降雨和初始地下水对浅层边坡稳定的综合影响

马世国^{1, 2}，韩同春^{1, 2}，徐日庆^{1, 2}

(1. 浙江大学 浙江大学滨海和城市岩土工程研究中心，浙江 杭州，310058；

2. 浙江大学 浙江大学软弱土与环境土工教育部重点实验室，浙江 杭州，310058)

摘要：下部为基岩的浅层残积土边坡多含有地下水，通过对传统Green-Ampt入渗模型的延伸，研究含有地下水的残积土边坡强降雨入渗过程；在强降雨入渗条件下，湿润区和地下水范围内基质吸力消失，湿润峰处和基岩面处为2个潜在的危险滑动面，分别对边坡在其上稳定性进行分析，并将二者统一起来，建立考虑强降雨和初始地下水共同作用下边坡的稳定分析模型。研究结果表明：下部含有初始地下水的浅层边坡在强降雨入渗期间，由于上部土体自重的增加，边坡最危险滑裂面在湿润峰和基岩面之间可能发生转移，边坡有可能在基岩处提前于湿润峰处破坏；同时，黏聚力越小，地下水位越浅，降雨入渗期间边坡在地下水下部基岩处破坏的可能性就越大，且土体黏聚力的影响最为显著。

关键词：强降雨入渗；初始地下水；湿润峰；Green-Ampt入渗模型；边坡稳定

中图分类号：TU441           文献标志码：A         文章编号：1672-7207(2014)03-0803-08

Integrated effect of intense rainfall and initial groundwater on slope stability

MA Shiguo^{1, 2}, HAN Tongchun^{1, 2}, XU Riqing^{1, 2}

(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;

2. Key Laboratory of Soft Soils and Geoenvironmental Engineering, Ministry of Education,

Zhejiang University, Hangzhou 310058, China)

Abstract: Most of the shallow residual soil slopes with bedrock beneath have groundwater, so the infiltration process of slope under intense rainfall was analyzed based on the extended Green-Ampt infiltration model; Because of the vanishing of matric suction in the wetting zone and the groundwater zone under intense rainfall, the slope stability analysis at the wetting front and the bedrock surface under the groundwater were studied respectively, and which were unified to establish a integrated stability analysis model during intense rainfall. The results show that the worst sliding surface probably devolves between the wetting front and the bedrock surface due to the increasing unit weight of soils during rainfall infiltration, the slope failure may occur firstly at the bedrock surface under groundwater, and not at the wetting front. Meanwhile the smaller cohesive strength and shallower groundwater table will cause more probability of slope failure at the bedrock surface under groundwater, and the influence of cohesive strength is the greatest.

Key words: intense rainfall infiltration; initial groundwater; wetting front; Green-Ampt infiltration model; slope stability

天然边坡表面大多为残积土所覆盖，而这些残积土往往为孔隙率大和黏聚力小的非饱和砂性土，土体存在负的孔隙水压力^[1]，即大家所说的基质吸力，黏聚力和负的孔隙水压力往往对砂性土质边坡的稳定起着至关重要的作用。降雨入渗是非饱和土边坡产生滑坡的重要因素^[2]，在强降雨入渗条件下，雨水的侵入导致非饱和土坡中基质吸力的降低或消失，因此湿润区土体抗剪强度降低，这在一定程度上增加了滑坡发生的可能性^[3-6]，同时，表层残积土自重增加，湿润区土体下滑力增加，边坡的稳定性也会显著降低。许多学者将湿润峰作为一个危险滑动面来考虑^[3-5]，然而这些残积土边坡下部往往含有不透水的基岩层，源源不断的地下水在不透水的基岩表面形成，地下水位以下至基岩面土体基质吸力消失，基岩面成为了一个潜在的危险滑动面。由于上部土体随着雨水的入渗自重不断增加，边坡在湿润峰处和基岩表面的安全系数均不断降低。强降雨入渗期间，湿润峰处和基岩表面为两个潜在的危险滑动面。国内外学者对于边坡的降雨入渗以及地下水位的影响进行了大量研究^[4-16]。Kenneth 等^[4]基于传统的Green-Ampt入渗模型，提出了一个简单的入渗分析方法用于评估湿润峰的发展，进而计算不同时刻非饱和土边坡的稳定性；由于雨水侵入导致非饱和土基质吸力的减小或消失，Sung^[5]研究了降雨入渗条件下无限长双层边坡的失效过程，建立了双层边坡雨水入渗模型，并应用该模型分析双层边坡稳定性；林鸿州等^[8]通过降雨诱发边坡失稳的模型试验来探讨降雨特性对边坡失稳的影响，选取合适的雨量预警参数；周家文等^[9]通过二维渗流-应力耦合分析，研究降雨入渗过程中对边坡的孔隙水压力、位移及安全系数的影响；刘才华等^[12]研究了地下水对库岸边坡稳定性的影响，分析了地下水引发库岸边坡失稳的机理，指出边坡岩土体介质因饱水软化作用其滑动面的力学参数值降低；王智磊等^[14]采用时间序列分析法在坡体表面位移与地下水位之间建立联系，根据地下水位变化规律预测坡体位移变化趋势。然而这些研究大多考虑单一条件下边坡的稳定，很少将降雨入渗和地下水二者统一起来。因此，本文作者通过研究无限长残积土边坡在降雨入渗条件下地下水下部不透水基岩处和湿润峰处安全系数的变化，将二者结合起来，建立整个边坡入渗期间的稳定分析模型。文中还针对不同黏聚力、地下水位L以及土体初始重度γ对边坡稳定分析模型给予讨论。

1  延伸的Green-Ampt入渗模型

对于饱和土的渗流问题通常可用Darcy定律进行求解，无需考虑土体基质吸力的作用。对于非饱和土的渗流问题变得较为复杂，用Richards方程来进行描述较为精确，但是由于其模型表述形式复杂，而且需要土壤水分运动参数，其求解必须采用解析法或者数值法，不便应用于实际的入渗过程分析。

为寻求一个能够表述土壤入渗特性较为简单的形式，Green和Ampt提出了经典的Green-Ampt入渗模型^[17]，如图1所示。

图1  Green-Ampt 入渗模型

Fig. 1  Green-Ampt infiltration model

Green-Ampt入渗模型最初仅适用于土质均匀、初始干燥的薄层积水条件的入渗，在剖面上对其均匀的入渗过程做了概化与假定，其中最基本的假定是入渗过程中湿润锋面始终为一个干湿截然分开的界面，即湿润区为饱和含水量θ_s，湿润锋前为初始含水量θ_i，因此土壤水分剖面分布呈阶梯状，故该模型又称之为活塞模型。模型如下：

             (1)

式中：i_w为入渗率；K_s为饱和渗透系数；S_f为湿润锋处平均基质吸力水头；z_f为概化湿润锋的深度；h₀为地表处的积水水头。

对于无限均质土，由上述模型进一步可以得到下列关系：

累计入渗量F

                (2)

式中：△θ=θ_s-θ_i为湿润区湿润前后含水量差。

湿润峰深度随时间的函数关系z_f~t

      (3)

该模型类似于Darcy定律，形式简单。然而该模型没有考虑在降雨初始表面积水前的入渗分析。因此，假设降雨强度i大于边坡土体的饱和渗透系数K_s(i＞K_s)，并将整个边坡的雨水入渗过程分为如下2个阶段：

(1) 阶段1：0≤t≤t_p(t_p为降雨开始到土体表面发生积水的时间)。在降雨入渗初期，降雨强度i小于土体的初始入渗能力，所有的雨水将渗入土体中而没有任何的坡面积水或径流，经过时间t_p，整个湿润区饱和，表面开始积水。此阶段有如下关系：

入渗量F

             (4)

                (5)

坡面径流发生时，降雨强度i等于土体的入渗能力i_w，即如下关系

           (6)

               (7)

式中：z_p为坡面径流发生时湿润峰的深度。

联立式(5)和(7)，得

              (8)

(2) 阶段2：t＞t_p。坡面积水后，由于坡面径流，边坡难以有积水存在，即在边坡入渗分析时取h₀=0，结合式(3)以及边界条件t=t_p，z_f=z_p。表面产生径流后湿润峰随时间的函数关系z_f~t

        (9)

因此，综合以上2个阶段的入渗过程分析，边坡的入渗控制方程应为：

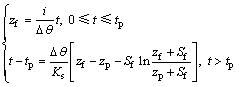   (10)

2  非饱和土边坡稳定性分析

在降雨入渗条件下，非饱和土边坡发生浅层破坏最为常见，且多为平行于边坡表面破坏^{[3, 5, 7, 14]}。对于下部含有基岩的浅层残积土边坡，在降雨入渗条件下由于湿润区基质吸力的降低，最危险面往往发生在湿润峰或潜在的积水面处^{[4-5, 14]}。当下部基岩含有初始地下水时，地下水位以下土体基质吸力消失，水的浮托力沿深度增加，基岩表面处水的浮托力最大且随着湿润区土体自重的增加，基岩表面同样为一潜在的危险滑动面。

浅层残积土边坡下部多为低透水性基岩，这里作如下假设：(1) 分析对象为一无限边坡；(2) 地下水面近似平行于坡面以及基岩表面；(3) 湿润峰为一平行于坡面的近似平面；(4) 考虑其无限长浅层边坡，湿润峰到达地下水位之前原地下水位基本保持不变；(5) 由于坡面径流，坡面无积水产生；(6) 不计土条间水平作用力的影响。

图2(a)所示为边坡稳定分析图，图2(b)和图2(c)所示分别为图2(a)中湿润区和土层厚度范围内相应单位宽度土条分析图。H为基岩表面土层厚度；H_w为地下水的深度；z_f为湿润峰深度；W₁为湿润区单位宽度土条的质量；W₂为基岩表面土层厚度范围内单位宽度土条的质量；a为边坡角；u_a和u_w分别为土条底部孔隙气压力和孔隙水压力；τ_m为相应土条底部的切应力；σ_n为土条底部斜面上正应力。

边坡的安全系数可由土体总的抗滑力与下滑力之比来求解，抗滑力由非饱和土抗剪强度公式求解，下滑力即为土体总的重度沿坡面的分量。即根据非饱和土摩尔库伦失效准则^[17]和极限平衡法得到边坡安全系数如下形式：

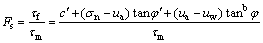  (11)

式中：τ_f为非饱和土抗剪强度；c'和j'分别为土的有效黏聚力和有效内摩擦角；(u_a-u_w)为土条底部基质吸力值；tan^bj为抗剪强度随基质吸力(u_a-u_w)增加而增加的速率。

2.1  边坡在湿润峰处稳定分析

对于大面积的浅层边坡，强降雨将导致非饱和土中气体难以自由排出，随着湿润峰的缓慢下移，湿润区土体原有的负孔隙水压力消失，即基质吸力(u_a-u_w)为0。假设湿润区土体饱和，湿润区土体采用最危险

的情况有效重度计算，结合湿润峰深度范围内单位宽度土条受力分析图2(b)可知，湿润区单位宽度土条底部的正应力和切应力分别为：

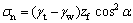
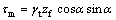
式中：γ_w为水的重度；γ_t为土的饱和重度。

图2  下部含地下水的浅层边坡分析图

Fig.2  Sketch of shallow slope with groundwater beneath

结合式(11)，边坡在湿润峰处安全系数可用湿润区土条总的抗滑力与下滑力之比来表示：

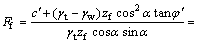
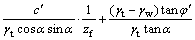     (12)

2.2  边坡在基岩表面处的稳定分析

由于地下水位至基岩表面范围内，基岩面处水的浮托力最大且基质吸力为0，随着雨水的不断入渗，土层厚度范围内土体自重不断增加，边坡在基岩处的安全系数也在不断减小。结合土条受力分析图2(c)可得：

式中：γ₀为土的初始重度，若为干土则γ₀=γ_d，γ_d为干重度。其中，地下水位H_w以下土的正应力计算采用有效重度，滑动力和切应力采用总重度。

结合式(11)，边坡在基岩表面处的安全系数求解，可用整个土层厚度范围内土条总的抗滑力与下滑力之比来表示：

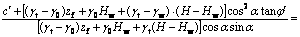
    (13)

从式(13)可看出：对于给定的某一湿润峰深度z_f和地下水深度H_w，在地下水位以下至基岩深度范围内安全系数F_H随土层深度H的增加逐渐减小。因此，除湿润峰处外土层底部的基岩表面成为了潜在的最危险滑动面，在降雨入渗期间需对其重点监测和分析。

2.3  边坡的安全系数分析

在雨水入渗初期，由式(12)第1项可知：边坡土体黏聚力不为0时，分母中z_f从0不断增大，F_f将从无穷大开始呈指数减小；同时由式(13)可知，当分母中z_f从0不断增大时，F_H将从一定值F_Hi不断减小，F_Hi为具有初始地下水位的边坡在降雨前边坡的最小安全系数。其值为

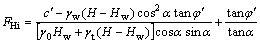
因此，在降雨初期必有F_f＞F_H，此阶段式(13)适用于计算边坡的安全系数。当达到某一时刻t₀时，F_f减小到使得F₀=F_f=F_H(F₀为t₀时刻边坡所对应的安全系数)，t₀后边坡的安全系数计算应采用式(12)。

联立式(12)和(13)，令F_f=F_H，得到边坡在湿润峰处安全系数与基岩表面处安全系数相等时湿润峰的位置z₀

           (14)

其中： ； ； 。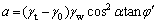

结合式(10)，可以求得相应t₀。边坡安全系数的计算应分以下2种情况：

    当F₀≤1时，边坡的安全系数直接由式(13)求解，在雨水入渗过程中，湿润峰z_f达到z₀之前边坡在基岩表面即发生破坏。

当F₀＞1时，边坡的安全系数应有式(12)求解，在雨水入渗过程中，湿润峰z_f超过z₀后边坡在湿润峰z_f处发生破坏。

在整个强降雨入渗过程(i＞K_s)中边坡的安全系数统一表达式可表示为：

3  算例分析与讨论

为验证上述入渗模型的有效性和讨论边坡在基岩面和湿润峰处安全系数的变化情况。假设有一无限长浅层边坡，上覆H=2.00 m厚的砂质壤土层，下部为不透水基岩层，地下水位位于坡面下1.40 m处，且平行于坡面，边坡角度为33.7(坡度比为1:1.5)，如图3所示。图中AB，BC和CD为降雨入渗边界，DE为排水边界，分析中假定整个边坡的初始负孔隙水压力水头为7.0 m，壤土覆盖层的初始重度近似为干重度γ₀=γ_d。计算参数数值如表1，土水特征曲线和渗透系数曲线如图4和图5所示。降雨强度i为3.6 cm/h，采用seep/w分析软件对边坡进行渗流模拟，由于坡面径流，假设降雨期间并未在坡面产生积水。

3.1  渗流分析

图6所示为数值模拟和延伸的Green-Ampt入渗模型计算结果。从图6可以看出：模拟结果与模型计算结果相当吻合，当湿润峰达到13.5 cm时，边坡表面开始积水，产生坡面径流。模型计算结果显示整个边坡被饱和需t_H=20.8 h(t_H为整个边坡饱和所需时间)的时间，而数值模拟的结果为t_H=19.44 h，已相当接近，其之所以产生误差，是由于地下水位上方一定范围内土体含水量较大，结合式(9)，当湿润峰接近地下水位时，单位深度土体饱和所需含水量差△θ减小，导致时间t缩短。

图3  边坡数值分析模型

Fig. 3  Numerical model of slope

图4  土的土水特征曲线

Fig. 4  Soil-water characteristic of soil

表1  砂质壤土的计算参数

Table 1  Parameters of soil

图5  土的渗透系数曲线

Fig. 5  Hydraulic conductivity curve of soil

图6  湿润峰深度z_f~t变化曲线

Fig. 6  Wetting front depth-time curves

3.2  稳定分析

图7所示为在降雨入渗条件下随着湿润峰的下移边坡在基岩面H深处和湿润峰z_f处的安全系数对比曲线。从计算结果可以看出，雨水入渗发生以后，湿润峰下移至z₁=100 cm(z₁＜z₀=120 cm)时，由于土的重度逐渐增加，边坡在基岩面H处安全系数降为1，F_s=1，而此时边坡在湿润峰z_f处安全系数为1.13，也就是说降雨入渗发生以后，该边坡将在基岩面处提前破坏，而这往往是大多数学者所忽略的，只考虑了湿润峰处的破坏。

图7  安全系数F_s-z_f 变化曲线

Fig. 7  Slope safety factor F_s-z_f curves

雨水入渗至z₀处之前，边坡的最危险滑动面在基岩面处，当雨水入渗到z₀处时，边坡在基岩面和湿润峰z₀处的安全系数相等(F₀=0.99＜1)，超过z₀处时边坡的最危险滑动面发生转移，湿润峰处成为了潜在的最危险滑动面，由于F₀=0.99＜1该算例应按式(13)来计算边坡的稳定性。

由图7可以看出，边坡在湿润峰处的安全系数呈指数降低，而边坡在基岩面处的安全系数降低缓慢。但是对于黏聚力较小的风化土层，当下部含有地下水时，由于地下水导致下部土体基质吸力的消失，边坡本身处在一个较危险情形。一旦遇到强降雨，由于土体自重的增加，边坡在地下水位下部的基岩面处破坏更易发生。

因此，在降雨入渗条件下，含有地下水的残积土边坡的稳定性计算，应分别对地下水下部的基岩面和湿润峰面统一计算分析，即式(15)所示，通过确定z₀的位置，得到边坡在整个强降雨过程中的安全系数随时间变化的关系。

3.3  不同黏聚力对z₀和F₀的影响

在本算例基础上改变黏聚力，得到图8在4种黏聚力下z₀和F₀的变化关系。图中显示黏聚力越大，z₀和F₀就越大，当F₀＞1时，随着雨水的入渗边坡将在湿润峰z_f处某一时刻提前破坏，此时边坡在地下水范围内的稳定性可不予考虑；当F₀＜1时，随着雨水的入渗边坡将在地下水下部不透水基岩处某一时刻提前破坏，此时变化的湿润峰z_f处可不予考虑。也就是说，黏聚力越大，降雨入渗期间，土坡在变化的湿润峰z_f处发生滑坡的可能性越大。黏聚力越小，土坡在地下水范围内发生滑坡的可能性越大。因此，对于含有地下水的浅层风化土坡，黏聚力较小，当遇到强降雨时，在地下水范围内尤其不透水基岩面处极易发生滑坡。

图8  不同黏聚力下z₀和F₀的变化

Fig. 8  Slope safety factor F₀-z₀ curve with different cohesive strengths

3.4  地下水位深度H_w对z₀和F₀的影响

保持本算例其他参数不变，改变地下水位H_w，可得到图9所示的z₀和F₀的变化关系。由图9可知：地下水位越深，z₀和F₀反向相关，z₀增大，F₀减小。当保持土层总厚度H不变时，地下水位越浅，F₀越小，随着雨水的入渗边坡将在地下水以下基岩处某一时刻提前破坏。也就是说，地下水位越浅，降雨入渗发生以后边坡在地下水范围内尤其基岩处发生滑坡的可能性就越大。

3.5  边坡土体初始重度对z₀和F₀的影响

图10所示为不同初始重度下z₀和F₀的变化。从图10可以看出：在不同的初始重度γ₀下，z₀和F₀也反向相关，随着残积土边坡初始重度的增加，F₀减小，但是，F₀的变化量近乎可以忽略。因此，可以推断，同一种土体，土体不同的初始重度对可能的滑裂面发生的位置影响很小。本算例在残积土为干重度时F₀＜1，因此不管土体初始含水量多大，降雨入渗时，边坡将在地下水位L处提前破坏。对于同一种土体，土体不同的初始重度对潜在的滑裂面发生的位置影响很小，可以忽略。

图9  不同地下水位H_w下z₀和F₀的变化曲线

Fig. 9  Slope safety factor F₀-z₀ curve with different groundwater tables

图10  不同初始重度下z₀和F₀的变化

Fig. 10  Slope safety factor F₀-z₀ curve with different initial weight of soil

由以上分析可知：土体的黏聚力对滑裂面位置的影响较为显著。黏聚力越小，地下水位越浅，当遇到强降雨时，在地下水范围内尤其不透水基岩面处极易发生滑坡。

4  结论

(1) 通过对传统Green-Ampt入渗模型的延伸，研究了含有地下水的残积土边坡强降雨入渗过程。数值模拟表明，延伸的入渗模型具有较好的适用性。

(2) 对于风化的残积土边坡，在整个降雨入渗期间，边坡潜在的最危险滑动面，既有可能在湿润峰处，又有可能在下部的基岩面处。本文将边坡湿润峰处和基岩处的稳定分析统一起来，建立了整个降雨入渗期间边坡最小安全系数计算模型。

(3) 在强降雨期间，边坡在地下水下部基岩处可能提前于湿润峰处破坏。这在一定程度上也揭示了部分地区雨期较早发生滑坡事故的原因，对于含地下水的浅层边坡降雨安全预报具有较好的指导作用。

(4) 黏聚力越小，地下水位越浅，在地下水范围内尤其不透水基岩面处发生滑坡的可能性就越大。

参考文献：

[1] Fredlund D G, Raharajo H. Soil mechanics for unsaturated soils[M]. New York: Wiley Inter-science, 1993.

[2] 陈祖煜. 土质边坡稳定分析:原理、方法、程序[M]. 北京: 中国水利水电出版社, 2003: 1-3.

CHEN Zuyu. Soil slope stability analysis: Theory, methods and applications[M]. Beijing: China Water Conservancy and Hydropower, 2003: 1-3.

[3] Rahardjo H, Lim T T, Chang M F, et al. Shear-strength characteristics of a residual soil[J]. Canadian Geotechnical Journal, 1994, 32(1): 60-77.

[4] Kenneth G, Xue J. A simple method to analyze infiltration into unsaturated soil slopes[J]. Computers and Geotechnics, 2008, 35(2): 223-230.

[5] Sung E C. Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics[J]. Engineering Geology, 2009, 105(1/2): 32-43.

[6] Brooks S M, Richards K S. The significance of rainstorm variations to shallow translational hillslope failure[J]. Earth Surface Processes and Landforms, 1994, 19(1): 85-94.

[7] Fourie A B, Rowe D, Blight G E. The effect of infiltration on the stability of the slopes of a dry ash dump[J]. Geotechnique, 1999, 49(1): 1-13.

[8] 林鸿州, 于玉贞, 李广信, 等. 降雨特性对土质边坡失稳的影响[J]. 岩石力学与工程学报, 2009, 28(1): 198-204.

LIN Hongzhou, YU Yuzhen, LI Guangxin, et al. Influence of rainfall characteristics on soil slope failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 198-204.

[9] 周家文, 徐卫亚, 邓俊晔, 等. 降雨入渗条件下边坡的稳定性分析[J]. 水利学报, 2008, 39(9): 1066-1073.

ZHOU Jiawen, XU Weiya, DENG Junye, et al. Stability analysis of slope under the condition of rainfall infiltration[J]. Shuili Xuebao, 2008, 39(9): 1066-1073.

[10] 姚海林, 郑少河, 陈守义. 考虑裂隙及雨水入渗影响的膨胀土边坡稳定性分析[J]. 岩土工程学报, 2001, 23(5): 606-609.

YAO Hailin, ZHENG Shaohe, CHEN Shouyi. Analysis on the slope stability of expansive soils considering cracks and infiltration of rain[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 606-609.

[11] 徐晗, 朱以文, 蔡元奇, 等. 降雨入渗条件下非饱和土边坡稳定分析[J]. 岩土力学学报, 2005, 26(12): 1957-1962.

XU Han, ZHU Yiwen, CAI Yuanqi, et al. Stability analysis of unsaturated soil slopes under rainfall infiltration[J]. Rock and Soil Mechanics, 2005, 26(12): 1957-1962.

[12] 刘才华, 陈从新, 冯夏庭, 等. 地下水对库岸边坡稳定性的影响[J]. 岩土力学学报, 2005, 26(3): 419-422.

LIU Caihua, CHEN Congxin, FENG Xiating, et al. Effect of groundwater on stability of slopes at reservoir bank[J]. Rock and Soil Mechanics, 2005, 26(3): 419-422.

[13] 马崇武, 刘忠玉, 田君. 地下水位升高时黏性土无限边坡的水平位移[J]. 岩土力学学报, 2008, 29(5): 1249-1253.

MA Chongwu, LIU Zhongyu, TIAN Jun. Horizontal displacements in infinite slopes of cohesive soil due to raise of groundwater table[J]. Rock and Soil Mechanics, 2008, 29(5): 1249-1253.

[14] 王智磊, 孙红月, 尚岳全. 基于地下水位变化的滑坡预测时序分析[J]. 岩石力学与工程学报, 2011, 30(11): 2276-2284.

WANG Zhilei, SUN Hongyue, SHANG Yuequan. Time series analysis of landside prediction based on groundwater level variation[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(11): 2276-2284.

[15] Muntohar A S. An integrated infiltration and slope stability model for predicting rainfall induced landslides along a mountain road in Taiwan[D]. Taiwan: The National Taiwan University of Science and Technology. Department of Construction Engineering, 2008: 1-121.

[16] Gavin K, Xue J. Use of a genetic algorithm to perform reliability analysis of unsaturated soil slopes[J]. Geotechnique, 2009, 59(6): 545-549.

[17] Fredlund D G, Morgenstern N R, Widger R A. The shear strength of unsaturated soil[J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321.

(编辑  陈爱华)

收稿日期：2013-03-18；修回日期：2013-06-18

基金项目：国家自然科学基金资助项目(51178423)

通信作者：韩同春(1968-)，男，河南卫辉人，博士，副研究员，从事边坡稳定性方面的研究；电话：0571-88208780；E-mail: htc@zju.edu.cn