J. Cent. South Univ. (2012) 19: 1419-1424

DOI: 10.1007/s11771-012-1158-3

Energy dissipation of cavity expansion based on generalized non-linear failure criterion under high stresses

ZOU Jin-feng(邹金锋), TONG Wu-qi(童无欺), ZHAO Jian(赵健)

School of Civil Engineering, Central South University, Changsha 410075, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: Based on the compression mechanism for analyzing the cavity expansion problem in soil under high stresses, generalized non-linear failure criterion and large strain and energy conservation in plastic region during the cavity expanding were adopted. The energy conservation equation was established and the limited pressure of cavity expansion under high stresses was given based on the energy dissipation analysis method, in which the energy generated from cavity expansion is absorbed by the volume change and shear strain caused in soil. The factors of large strain and dilatation were considered by the proposed method. The analysis shows that the limited pressure is determined by failure criterion, stress state, large deformation characteristic, dilatation and strength of soil. It is shown from the comparison that the results with the proposed method approximate to those of the in-situ method. The cavity expansion pressure first decreases and then increases nonlinearly with both of shear modulus and dilatation increasing.

Key words: energy dissipation; energy conservation; large strain; cavity expansion; high stress

1 Introduction

The cavity expansion theory is widely used in the field of geotechnical engineering, especially for calculating the ultimate bearing capacity of foundation, analyzing pile driving, cone penetration test and compacting grouting, etc [1-6]. FAN et al [7] and other earlier researchers assumed that the soil mass of plastic zone around the cavity is incompressible by using the pure shear method, without considering the influence of volume strain. The theory substance regards the process of pile or cone penetration as a local shear failure. However, the soil mass failure is controlled by compression mechanism and volume strain can never be neglected during the pile driving, cone penetration and compacting grouting. In the 1960s, LADANYI [8] observed the volume strain phenomenon in plastic region from the stress-volume strain relationship test results of saturated clay, and brought it into analyzing cavity expansion. And in succession, the author gave the theoretical solution of cavity expansion considering the volume strain in the plastic zone [1].

However, in the current researches on cavity expansion, the factors such as the shear dilatancy, strain softening, radius of the plastic zone and cavity expansion pressure are considered, based on the assumption of the perfectly elasto-plastic solid and small deformation theory. Though there are still several conclusions [9-13] by using the failure criterion of Mohr-Coulomb or Cambridge Model considering the non-associated flow, the expansion pressure and excess pore water pressure are studied for strain hardening solid. The essence of these results belongs to the elasto-plastic mixed subject based on the shear mechanism. Although they accumulated lots of results considering the volume strain in the plastic zone, it is hard to make quantitative analysis for static cone penetration test and pile driving, especially in the high-stress soil. ZHANG [14] modified the expansion pressure for the spherical cavity expansion in sands under high stress without large deformation and the non-associated flow rule after yielding. Actually, it is a consensus in geotechnical engineering field that the soil mass will cause large deformation in the process of the cone penetration test and pile driving, and the plastic deformation obeys the non-associated flow rule. ZOU et al [15] obtained the cavity expansion pressure in sands under high stress considering the large deformation, volume change and non-associated flow rule with energy and volume change conservation method. However, the developed theory did not consider high stresses and large strain in clay.

Currently, it remains a challenging subject for using the energy method to analyze the cavity expansion under high stresses considering large strain and energy conservation in plastic region. It is the main subject in this work to consider comprehensively the factors of large strain, energy conservation, and generalized nonlinear failure criterion for analyzing cavity expansion problem under high stresses with energy dissipation analyzing method.

In this work, according to the compression mechanism and the stress-strain-volume strain relationships under high stresses, the generalized non-linear failure criterion, large strain, and the theory of energy conservation in the process of cavity expansion were adopted. From the comparisons between the proposed method and in-situ results, the formulation for cavity expansion pressure was obtained.

2 Basic assumption

2.1 Theory basis

The penetrating persistence increases gradually when the static cone test or pile toe penetrates into the soil mass. Some regions begin to yield and absorb part of volume generated by penetration. With the increase of penetration, the compression region expands gradually and reaches an equilibrium state. In this region, the volume compression of soil equals the whole volume of penetration instrument until penetration is over and penetrated resistance tends to be a steady value. In a certain region around the penetration device, the compression instrument of soil is compensated by part of penetration volume and the continuum penetration displacement is ensured. The energy loss of penetration should be equal to that needed by the volume strain and deformation of the circumambient soil mass and the energy loss of volume strain occupies the main part.

In order to simplify the analysis, the soil mass around cavity can be divided into two regions: the plastic region and the elastic region, as illustrated in Fig. 1.

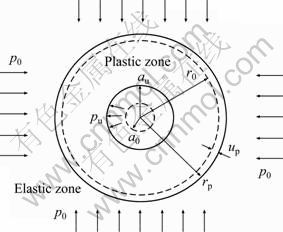
Fig. 1 Sketch of cavity expansion

Figure 1 shows a cavity with an initial radius a₀ and an initial internal pressure p₀. Compressive stress and strain are taken as positive. The cavity expands to a radius of a and meanwhile the internal cavity pressure increases from p₀ to p_u. Correspondingly, an element initially at a distance r₀ from the center of the cavity wall moves to a new radial position r from the center. A zone of soil around the cavity will deform plastically when the internal pressure exceeds the yield pressure in the cavity. The radial distance of the plastic zone around cavity is denoted by r_p and the displacement of the elastic/plastic interface is denoted by u_p. The soil beyond the plastic zone would remain in a state of elastic equilibrium. The property of the soil in the elastic zone is defined by elastic modulus E, and Poisson ratio v.

Based on these assumptions, the condition of spherical symmetry holds in the expansion of a spherical cavity. Using a spherical polar coordinate system, the initial position of soil element around a spherical cavity can be described as (r₀, α, θ). The principal stresses σ_θ and σ_α are the same. Similarly, using a cylindrical polar coordinate system, the initial position of soil element around a cylindrical cavity can be described as (r₀, θ, z). Plane-strain conditions are assumed for the cylindrical cavity in the vertical direction. With these assumptions, the displacements in the medium are totally radial, and problem is essentially one-dimensional.

2.2 Basic hypothesis

Based on the theoretical analysis above, the development of analytical framework for the analysis of cavity expansion with energy method is based on the following assumptions:

1) The energy dissipation of the external stress during cavity expansion is mainly focused on a plastic region, in which the volume change generated by cavity expansion is absorbed by the deformation of the soil mass. Considering that the average normal stress of soil under elastic state in elastic and plastic region is comparatively small and the elastic deformation can be recovered, the energy dissipation and volume compression are too small to be observed, thus, they can be neglected.

2) The soil is homogeneous and contains a single cavity with radius in an unbounded three-dimensional space. A homogeneous state of stress, p₀, is assumed to act throughout the soil.

3) The soil is assumed to obey Hookian elasticity until the onset of yielding. Yielding of soil is described by the generalized non-linear failure criterion.

According to Ref. [16], the generalized non-linear failure criterion can be expressed as

    (1)

where σ_t is the three-dimensional extension strength, and M_f is the failure stress ratio under a given reference pressure p_r. For frictional materials, the range of frictional angle is 0°-90° and the corresponding range of M_f is 0< M_f <3. β is the material constant reflecting the influence of mean principal stress on strength, 0<β<1.

For cavity expansion problem, the octahedral normal stress p and octahedral deviator stress q in sand and clay can be written as

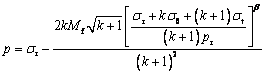   (2)

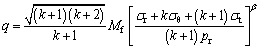    (3)

From Eqs. (2) and (3), the octahedral normal stress p_c and p, the octahedral deviator stress q_c and q are obtained.

According to Ref. [17], as the cavity continues to expand indefinitely (i.e. a₀/a→∞), the cavity radius a_u  can be related to the position of the elastic-plastic boundary as

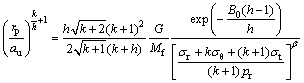                 (4)

where r_p is plastic region radius, a_u is cavity expansion radius, B₀=(σ_R-p₀)/(2G), σ_R is stress of interface between elastic and plastic region, and G is shear modulus [1].

3 Energy dissipation equation

3.1 Energy conservation equation

According to Ref. [17-18], energy conservation equation leads to

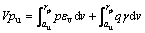                     (5)

where V, p, q, ε_v, γ and p_u represent the volume, normal stress, deviator stress, volume change, shear strain and expansion pressure, respectively.

3.2 Cavity expansion pressure

For cavity expansion, we have dv=2kπr^kdr. Ignoring higher-order terms of a₀, ≈ .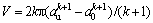

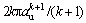By combing Eqs. (1), (2), (3), (4), and (5), the expansion pressures of cavity expansion for the clay soil and sand soil are obtained. Then, the problem can be resolved with the aid of numerical calculation.

4 Analysis of examples

4.1 Analysis of example for sand soil

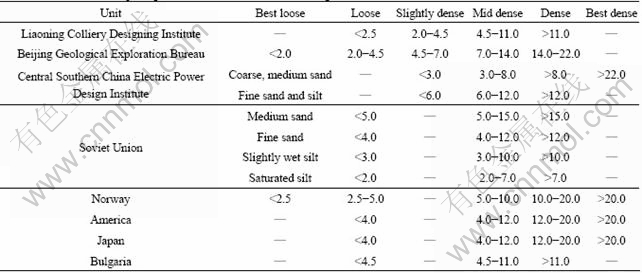
In order to evaluate the validity of the proposed method, some in-situ results of the resistance in static cone penetration for sand soil under high stresses are presented in Table 1 [14, 17].

It is found from Table 1 that the limited penetration resistance is no more than 5.0 MPa for loose sand, is less than 7.0 MPa for slightly dense sand, mainly ranges from 4.0 to 12.0 MPa for mid dense sand and is more than  7.0 MPa for dense sand. Therefore, the limited expanding pressure in penetration cone ranges from 10.0 to 20.0 MPa in most of the cases, though the limited penetration resistance of best loose sand is larger than 20.0 MPa.

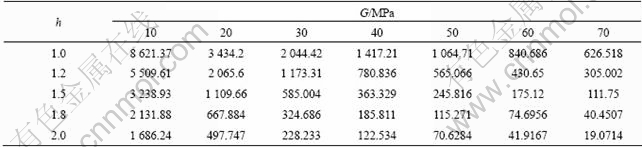
Table 2 and Table 3 present values of limited expansion pressure obtained by the proposed method for A=0.005 9, B=-0.004 2, C=0.009 2, σ=100 kPa, f=32.5°, v=0.27, γ=16.8 kN/m³, m=n=0.5, the embedment of soil mass of 15.9 m, p_r=1.8 MPa, M_f=1.3, β=0.56, σ_t=0 with parameters of h and G varying from 1.0 to 5.0 and from 10.0 to 70.0 MPa for spherical and cylindrical cavities, respectively [2].

Table 1 Limited values of p_s or q_c for sand-soil with different close-grained ratios

It can be seen from Table 2 that the limited expansion pressure of spherical cavity is between 1.9 MPa and 17.0 MPa, except 26.6 MPa for h=1.0 and G=10 MPa. The expansion pressure decreases with shear dilatancy (h) and shear modulus (G), and increases at first and then decreases.

It is shown in Table 3 that the limited expansion pressure of cylindrical cavity is between 0.3 and 7.6 MPa. The expansion pressures increase with both parameters of shear dilatancy (h) and shear modulus (G) increasing. The cylindrical cavity expansion pressure calculated by the developed theory is slightly larger than that obtained by VESIC’s theory. The result obtained by the proposed method is more approximated to the in-situ results than that obtained by VESIC’s theory.

In order to avoid the coincidence of the results, Table 4 and Table 5 present values of limited expansion pressure obtained by the developed theory for A=0.03 2, B=0.009, C=0.005 5, σ=100 kPa, f=33°, m=n=0.5, v=0.25, γ=18.6 kN/m³, the embedment of soil mass of 13.7 m, p_r=2.0 MPa, M_f=1.4, β=0.5, σ_t=0 with parameters of h and G varying from 1.0 to 2.0 and from 10.0 to 70.0 MPa for spherical and cylindrical cavities, respectively [2].

Table 4 shows that the limited expansion pressure of spherical cavity is between 0.1 and 20.0 MPa except 30.86 MPa for h=1 and G=10 MPa. The expansion pressure decreases with shear dilatancy and shear modulus increasing and this illustrates the influence of dilatation on expansion pressure.

Table 5 presents that the limited expansion pressure of cylindrical cavity is between 0.02 and 8.6 MPa. The expansion pressures decrease with shear dilatancy index and shear modulus increasing.

Table 2 Limited expansion pressure (kPa) of spherical cavity with different values of h and G

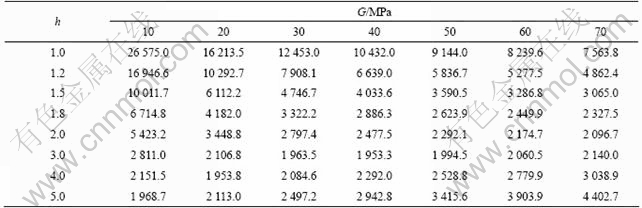
Table 3 Limited expansion pressure (kPa) of cylindrical cavity with different values of h and G

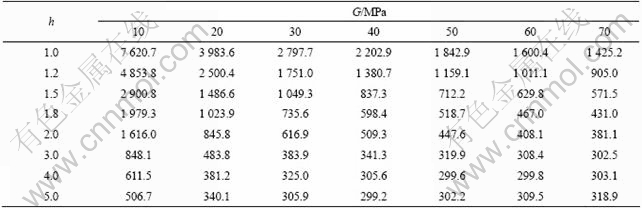
Table 4 Limited expansion pressure (kPa) of spherical cavity with different values of h and G

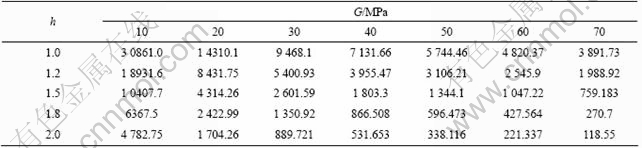
Table 5 Limited expansion pressure (kPa) of cylindrical cavity with different values of h and G

It can be found from the both examples that the results with the proposed method are more approximated to the in-situ results than those with VESIC’s theory [2]. Therefore, the comparison shows that the proposed method is an effective method for estimating the limited penetration resistance. The comparisons show that the proposed method is effective for evaluating the cavity expansion pressure with the analyzing method of energy dissipation.

4.2 Parameter analysis

In order to validate the analytical solutions, two examples were analyzed by using the proposed method for A=0.032, B=0.009, C=0.005 5, σ=100 kPa, ?=33°, m=n=0.5, v=0.25, γ=18.6 kN/m³, the embedment of soil mass of 13.7 m, p_r=1.65 MPa, M_f=1.6, β=0.6, σ_t=0 with parameters of h and G varying from 1.0 to 2.0 and from 10.0 to 70.0 MPa, respectively [2]. Figures 2 and 3 present the relationships between the limited cavity expansion pressure and both parameters of dilatation h and ratio r_p/a_u in sand soil for the condition of k=1 and k=2, respectively.

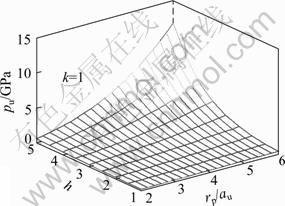
Fig. 2 Relation of p_u, h and r_p/a_u in cylindrical expansion (k=1)

The numerical simulation results from Fig. 2 and Fig. 3 show that the relationships are nonlinear under the conditions of spherical cavity expansion and cylindrical cavity expansion. The change tendency of p_u becomes more obvious with the increase of shear dilatancy index. The relationships between p_u and r_p/a_u are linear for h≤3.0, while become nonlinear for h≥3.0. The relationships between p_u and h become linear basically for r_p/a_u≤3.0. Meanwhile, the tendency of p_u changes more rapidly when the ratio r_p/a_u increases than dilatation h.

Figures 4 and 5 present the relationships between limited expanding pressures and both parameters of h and G for k=1 and k=2 in clay, respectively.

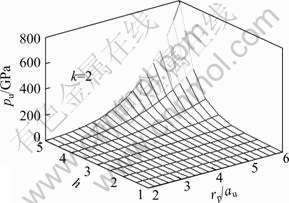
Fig. 3 Relation of p_u, h and r_p/a_u in spherical expansion (k=2)

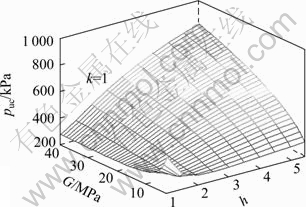
Fig. 4 Relation of p_uc, h and G in cylindrical expansion (k=1)

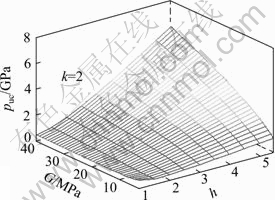
Fig. 5 Relation of p_uc, h and G in spherical expansion (k=2)

It can be seen from Fig. 4 and Fig. 5 that the relationships between p_uc and both of G and h are nonlinear and p_uc decreases at first and then increases as the parameters of G and h increase under the conditions of spherical cavity expansion and cylindrical cavity expansion. This is because more expansion pressure is needed to overcome the influence of shear dilation in initial, and then the strain softening makes the expansion pressure decrease. Furthermore, expansion pressure increases as the dilation disappears and the soil mass compacts gradually.

5 Conclusions

1) The formulations of cavity expansion pressure under high stresses in sand soil and clay are developed with energy conservation considering large strain. It is shown from comparisons that the cavity expansion pressures obtained by using the developed theory are slightly larger than those obtained by VESIC’s theory, and more approximated to the in-situ results than those by VESIC’s theory.

2) From the comparisons between theoretical and in-situ results, it can be found that the proposed method is valid and effective.

3) Due to the influence of shear dilation, the general relation between expansion pressure and shear modulus is nonlinear, and it decreases at first and then increases with shear modulus and dilatation increasing under the conditions of spherical and cylindrical cavity expansion.

References

[1] ZOU Jin-feng. Cavity expansion based on the linear and nonlinear failure criteria and its engineering applications [D]. Changsha: Central South University, 2007. (in Chinese)

[2] YANG Xiao-li, YIN Jian-hua. Slope equivalent Mohr-Coulomb strength parameters for rock masses satisfying the Hoek-Brown criterion [J]. Rock Mechanics and Rock Engineering, 2010, 43(4): 505-511.

[3] YANG Xiao-li. Seismic displacement of rock slopes with nonlinear Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 948–953.

[4] YANG Xiao-li, YIN Jian-hua. Estimation of seismic passive earth pressures with nonlinear failure criterion [J]. Engineering Structures, 2006, 28(3): 342-348.

[5] YANG Xiao-li, YIN Jian-hua. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267-273.

[6] YANG Xiao-li, SUI Zhi-rong. Seismic failure mechanisms for loaded slopes with associated and nonassociated flow rules [J]. Journal of Central South University of Technology, 2008, 15(2): 276-279.

[7] FAN Wen, YU Mao-hong, CHEN Li-wei. An analytic solution of elastoplastic pressure tunnel considering material softening and dilatancy [J]. Engineering Mechanics, 2004, 23(19): 3213-3220. (in Chinese)

[8] LADANYI B. Expansion of a cavity in a saturated clay medium [J]. Journal of the Soil Mechanics and Foundations Division, ASCE, l963, 90(SM4): l27-l6l.

[9] CAO L F, TEH C I, CHANG M F. Undrained cavity expansion in modified cam clay. I: Theoretical analysis [J]. Geotechnique, 2001, 51(4): 323-334.

[10] CAO L F, TEH C I, CHANG M F. Analysis of undrained cavity expansion in elastoplastic soils with non-linear elasticity [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(1): 25-52.

[11] COLLINS I F, YU H S. Undrained cavity expansions in critical state soils [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1996, 20(7): 489-516.

[12] YU H S, CARTER J P. Rigorous similarity solutions for cavity expansion in cohesive-frictional soils [J]. International Journal of Geomechanics, 2000, 2(2): 233-258.

[13] ROSENBERG Z, DEKEL E. Analytical solution of the spherical cavity expansion process [J]. International Journal of Impact Engineering, 2009, 36(2): 193-198.

[14] ZHANG Ji-ru. Problem of spherical cavity expansion in sands under high stresses [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(8): 1209-1214.

[15] ZOU Jin-feng, LUO Qiang, LI Liang, YANG Xiao-li, DAN Han-cheng. The compare of energy dissipation analysis method of cavity expansion considering the large strain and volume change in sand soil under high stresses respectively [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 426-432.

[16] YAO Yang-ping, LU De-chun, ZHOU An-nan, ZOU Bo. Generalized non-linear strength theory and transformed stress space [J]. Science in China Ser. E: Engineering & Materials Science, 2004, 47(6): 691-709.

[17] ZOU Jin-feng, PENG Jian-guo, ZHANG Jin-hua, LUO Heng, AN Ai-jun. Analytical solution of cavity expansion with the non-linear Mohr-Coulomb failure rule [J]. China Civil Engineering Journal, 2009, 42(7): 90-97.

[18] YANG Xiao-li, HUANG Fu. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686-691.

(Edited by YANG Bing)

Foundation item: Projects(2010RS4016, 10JJ60708) supported by Hunan Provincial Science Foundation, China; Projects(201018, 201108, 201121) supported by Hunan Provincial Transportation Science and Technology Progress and Innovation Plan of China

Received date: 2011-03-04; Accepted date: 2011-10-08

Corresponding author: ZOU Jin-feng, Associate Professor, PhD; Tel: +86-731-82656248; E-mail: zoujinfeng_0@163.com