文章编号: 1004-0609(2006)02-0322-05
再生核质点法模拟切分轧制过程
崔青玲, 李长生, 刘相华, 王国栋
(东北大学 轧制技术及连轧自动化国家重点实验室, 沈阳 110004)
摘 要: 为保证大变形弹塑性分析的稳定性, 采用随材料变形的拉格朗日物质形函数分析了整个切分轧制过程。 在整个变形过程中, 物质核函数的影响域包含相同的节点数, 通过坐标转换方法满足本质边界条件。 求解了切分轧制极端变形过程, 研究了不同切分楔夹角和轧件宽度对切分后轧件弯曲度的影响, 数值模拟结果与实验数据吻合良好。
关键词: 切分轧制; 无网格法; 弹塑性; 大变形
中图分类号: TG113 文献标识码: A
Splitting rolling simulation by reproducing kernel particle method
CUI Qing-ling, LI Chang-sheng, LIU Xiang-hua, WANG Guo-dong
(The State Key Laboratory of Rolling and Automation,
Northeastern University, Shenyang 110004, China)
Abstract: In order to assure the stability of the large deformation elastoplastic analysis, the Lagrangre material shape function deformed with material was used to analyze the splitting rolling process. And during the whole deformation process, the domain of the material kernel function includes similar nodes number. The transformation method is utilized to satisfy the essential boundary conditions. The splitting rolling is simulated, and the effects of different wedge angular and slab width on the split workpiece camber were studied. The simulation results accord well with the experiment ones in the literature.
Key words: splitting rolling; reproducing kernel particle method; elastioplastic; large deformation
金属切分轧制是指在轧制过程中, 将轧件用轧辊或其它设备沿纵向剖分成两条或多条轧件的材料加工新方法。 切分轧制过程发生严重不均匀变形和金属撕开过程。 采用有限元法(finite element method, FEM)模拟切分轧制时, 网格发生畸变, 需要重新划分网格, 但网格重划后, 节点场变量的传递降低了计算精度。 且在金属撕开时, 由于网格的限制, 采用FEM 无法继续求解[1, 2 ]。
无网格方法的出现解决了有限元法的上述局限性。 无网格方法将连续体离散为一组独立的节点, 基本场变量近似采用了基于节点的函数拟合, 从而可完全抛开网格的生成和重划, 摆脱了不连续性对问题的束缚[3-5]。 近年来无网格方法在金属成形领域得到了广泛应用, Chen等[6, 7]利用再生核质点法(reproducing kernel particle method, RKPM)模拟了环件压缩过程, Xiong等[8-10]将RKPM方法用于求解刚塑性材料的平面应变轧制过程, Bonet等[11] 采用(corrected smooth particle hydrodynamics, CSPH)完成了包括镦粗、 锻压等二维过程的变形形状模拟, 李长生等[12]采用CSPH方法求解了金属圆棒、 方棒和圆环大变形压缩过程。 Li等[13]采用(element free Galerkin method, EFG)方法模拟了弹塑性材料的平面应变镦粗过程和挤压过程。
采用无网格方法求解简单金属塑性变形过程已经取得了一定进展。 然而, 对于切分轧制过程等复杂金属变形过程, 由于边界条件以及极端变形等处理过程比较复杂, 采用无网格方法求解切分轧制过程目前还未见报导。
本文作者利用大变形弹塑性RKPM法, 采用随着材料变形的物质核函数以保证大变形过程的稳定性, 通过坐标转换满足本质边界条件[14], 求解了切分轧制问题, 数值模拟结果表明RKPM求解切分轧制大变形问题结果良好。
1 再生核质点法
Liu等[15]在积分转换的基础上对核函数进行修正, 提出再生核质点法, 即
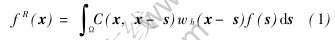
式中 fR(x)为函数f(x)的再生函数; C(x, x-s)为修正函数; wh(x-s)为核函数; s为积分哑元。
修正函数定义为
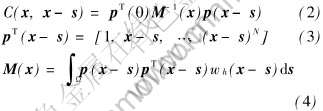
由于式(1)能够精确再生N阶多项式, 因此, 该方法满足N阶一致性条件。 式(1)的离散形式为
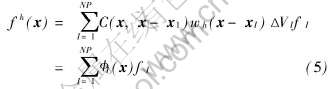
其中
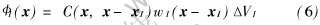
式中 NP为离散的节点总数; I(x)称为RKPM的形函数; fI是f(x)在节点I的函数值; ΔVI是和节点I有关的区域度量。 由于I(xJ)≠δIJ, fI不是fh(x)的节点值, 即fh(x)≠fI。
2 大变形弹塑性RKPM
2.1 变分原理
假设物体占据域Ωx, 边界为Гx, 从初始构形变形到当前构形Ωx, 边界为Гx。 物体受域Ωx中的体积力bi、 自然边界Γhix上的力hi、 本质边界Γgix上已知的边界位移gi的作用。 在笛卡儿坐标系中, 用X表示节点在初始构形Ωx中的位置, 在t时刻当前构形中的节点位置用映射函数x=φ(X, t)表示。 物体的运动由以下运动方程和初始条件描述:
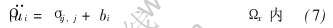
边界条件
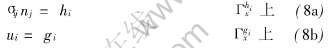
初始条件
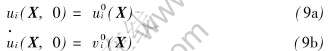
式中 ρ为密度; ni为当前构形表面的外法线; u0i为初始位移; v0i为初始速度;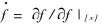 
为物质导数; 
为空间导数; σij为柯西应力; u(X, t)为物质位移。
变分原理叙述如下:
已知bi, hi, gi, u0i和v0i, 找到ui(X, t)∈H1g(H1g={u∶u∈H1, 在Γgix上ui=gi}), 使得对于所有的δui∈H10(H10={w∶w∈H10, 在Γgix上wi=0}, 则有
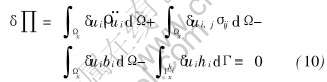
式中 H1为1阶Sobolev空间。
对非线性问题, 需要将式(10)线性化, 线性化后的变分方程为
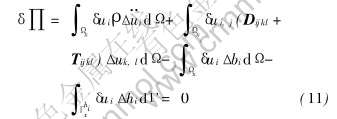
2.2 物质形函数
在RKPM计算中, 为保证稳定性, 核函数的影响域中必须包含足够的节点数[6]。 下面建立的随着材料变形的物质核函数, 在整个变形过程中, 物质核函数的影响域包含相同的节点数, 避免了大变形分析中的不稳定性。
物质形函数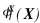
是建立在物质核函数Wxa(X-XI)和满足初始构形再生条件得到的, 即
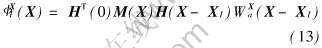
在变分方程中, 对位移的近似采用物质形函数更方便, 即
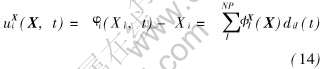
式中 diJ(t)为广义位移。
物质形函数的空间导数为
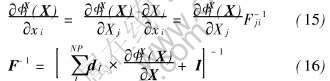
式中 I是单位张量。
2.3 坐标转换
由于无网格法的形函数不具有克罗内科尔性质, 本质条件需要通过拉格朗日乘子法或者罚函数法等方法解决, 这些方法有一定的局限性[16]。 下面介绍的方法将广义坐标转换为节点坐标, 建立了运动许可的近似函数和试函数, 从而能够直接处理本质边界条件。
利用坐标转换方法, 建立uhi(XJ, t)和diJ(t)之间的关系, 令
式中
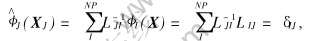
利用将广义位移转换为节点位移的方法, 使修正后的形函数具有克罗内科尔性质。 这种方法能够精确满足本质边界条件, 在非线性迭代过程中没有误差积累。
对式(11)引入物质形函数和坐标转换得到增量矩阵得到
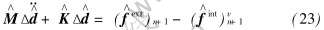
式中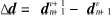 
, 为位移增量; 
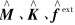和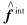 
分别是节点坐标下的质量矩阵、 刚度矩阵、 外力矢量和内力矢量。
3 切分轧制模拟
模拟计算条件为: 轧辊为刚性辊, 轧件材质为常温下铅, 其变形抗力模型为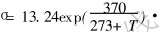 
, 抗拉强度σb=60MPa, 宽度b=37.5mm, 厚度h=12.5mm, 长度l=50mm。 轧辊直径d=125mm, 切分楔夹角θ=70°, 轧制速度v=0.5m/s, 摩擦因子μ=0.3。 由于对称性, 取上半部分, 如图1所示。 在变形大的区域即轧件中部网格划分较密, 而轧件边部由于几乎未变形, 网格划分较稀, 同样轧件厚度方向与轧辊接触处的网格也较密。
图1 切分过程示意图及轧件离散模型
Fig.1 Schematic diagram of splitting rolling and discretization model of slab
利用有限元分析时, 随着变形的继续, 在压下量达到64%时开始出现网格畸变。 图2所示为发生畸变的一个单元畸变前后的形状。 此时若要继续求解, 需要重新划分网格。
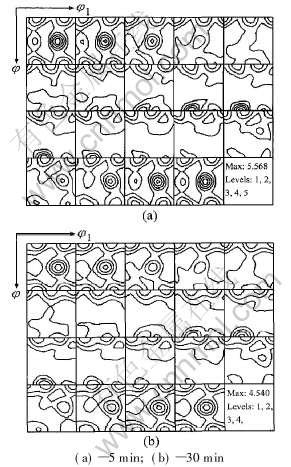
图2 畸变前后单元形状
Fig.2 Mesh shape of undeformed and deformed
而采用同样模型的无网格方法在求解过程中没有网格畸变。 当连接带上的横向应力超过抗拉强度时, 轧件被切分开, 切分后的轧件在水平面发生横向弯曲(见图3)。 这是由于切分轧制是一个不均匀变形过程, 被切分的轧件中部的纵向延伸率比两侧的纵向延伸率大, 纵向延伸率大的向纵向延伸率小的一侧弯曲。
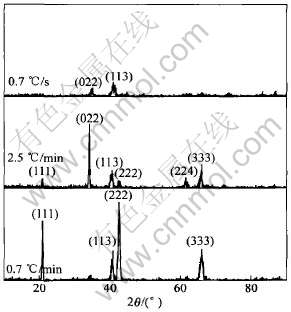
图3 被切分开的轧件示意图
Fig.3 Schematic diagrams of splitted workpiece
根据文献[17]中的实验数据, 研究不同切分楔夹角和轧件宽度对切分后轧件弯曲度的影响。 图4和5所示分别为相对切分弯曲度f=e/l(e为挠度)和宽展系数β=(bt-b)/b(bt为切分后两根轧件总宽度)随切分楔夹角和轧件宽度的变化情况。 从图4和5中可以看出, 模拟结果与实验数据吻合良好。
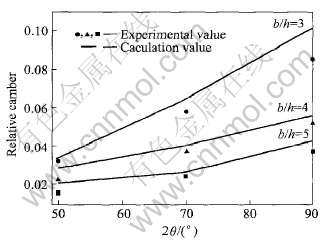
图4 相对弯曲度与楔角及轧件宽高比的关系
Fig.4 Relationship among relative camber and wedge angle and aspect ratio of slab
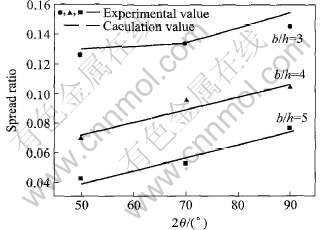
图5 宽展系数与楔角及轧件高宽比的关系
Fig.5 Relationship among spread ratio and wedge angle and aspect ratio of slab
4 结论
1) 利用大变形弹塑性再生核质点法模拟了切分轧制过程, 采用随材料变形的物质核函数以保证大变形过程的稳定性, 通过坐标转换满足本质边界条件。 无网格方法可以解决有限元法求解时遇到的网格畸变及金属撕开时无法求解的局限性, 数值模拟表明RKPM比FEM更适合求解大变形问题。
2) 分析了切分楔夹角和轧件宽度对切分后轧件弯曲度的影响, 结果表明模拟结果与文献中的实验数据吻合较好。
REFERENCES
[1]Taylan A. Numerical simulation for tool and process design in bulk metal forming[J]. Annals of the CIRP, 1996, 45(2): 599-610.
[2]Ping X, Tatsuhiko A. Roll pass evaluation for hot shape rolling process[J]. Journal of Materials Processing Technology, 1991, 27(3): 163-178.
[3]Belytschko T, Lu Y Y, Gu L. Element free Galerkin methods[J]. Int J Numer Meth Eng, 1994, 37(2): 229-256.
[4]Li S F, Liu W K. Meshfree and particle methods and their applications[J]. Applied Mech Review, 2002, 55(1): 1-34.
[5]Belytschko T, Lu Y Y, Gu L. Element free Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 1994, 37(2): 229-256.
[6]Chen J S, Pan C, Wu C T, et al. A Lagrangian reproducing kernel particle method for metal forming analysis[J]. Comp Mechanics, 1998, 22(3): 289-307.
[7]Chen J S, Roque C, Pan C. Analysis of metal forming process based on meshless method[J]. Journal of Materials Processing Technology, 1998, 80-81(3): 642-646.
[8]Xiong S W, Liu W K, Cao J. On the utilization of reproducing kernel particle method for the numerical simulation of plane strain rolling[J]. International Journal of Machine Tools & Manufacture, 2003, 43(1): 89-102.
[9]Xiong S W, Rodrigues J M C, Martins P A F. Application of the element free Galerkin method to thesimulation of plane strain rolling[J]. Eur J Mech A-Solid, 2004, 23: 77-85.
[10]Xiong S W, Liu W K, Cao J, et al. Simulation of bulk metal forming processes using the reproducing kernel particle method[J]. Comput Struct, 2005, 83: 574-581.
[11]Bonet J, Kulasegaram S. Correction and stabilization of smooth particle hydrodynamics methods with applications in metal forming simulations[J]. International Journal for Numerical Methods in Engineering, 2000, 47(6): 1189-1214.
[12]李长生, 熊尚武, Rodgigues J, 等. 金属塑性加工过程无网格方法数值模拟[M]. 沈阳: 东北大学出版社, 2004.
LI Chang-sheng, XIONG Shang-wu, Rodgigues J, et al. Metal Plastic Forming Process Simulated by Meshless Method[M]. Shenyang: North Eastern University Press, 2004.
[13]Li G Y, Belytscko T. Element-free Galerkin method for contact problems in metal forming analysis[J]. Engineering Computations, 2001, 18(1): 62-78.
[14]Chen J S, Pan C, Wu C T. Application of reproducing kernel particle methods to large deformations and contact analysis of elastomers[J]. Rubber Chemistry and Technology, 1998, 71( 2): 191-213.
[15]Liu W K, Jun S, Zhang Y F. Reproducing kernel particle methods[J]. Int J Numer Methods in Fluids, 1995, 20(8-9): 1081-1106.
[16]Belytschko T, Krongauz Y, Organ D, et al. Meshless methods: An overview and recent developments[J]. Comput Meth in Appl Mech Eng, 1996, 139(1-4): 3-47.
[17]马义德. 最佳辊楔切分轧制效果的研究[J]. 钢铁, 1997, 32(4): 41-45.
MA Yi-de. Study on optimum slit rolling by roll wedge[J]. Iron and Steel, 1997, 32(4): 41-45.
(编辑李艳红)
基金项目: 国家自然科学基金资助项目(50474016; 50534020)
收稿日期: 2005-06-08; 修订日期: 2005-09-25
作者简介: 崔青玲(1973-), 女, 讲师, 博士研究生
通讯作者: 崔青玲; 电话: 024-83687749; E-mail: Cuiql@mail.neu.edu.cn
