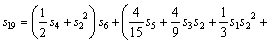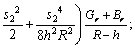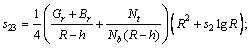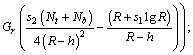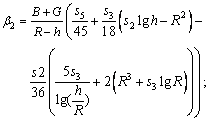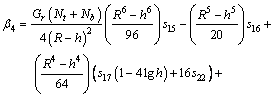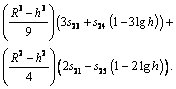Biomathematical study of time-dependent flow of a Carreau nanofluid through inclined catheterized arteries with overlapping stenosis
来源期刊:中南大学学报(英文版)2017年第11期
论文作者:Ashfaq Ahmed Sohail Nadeem
文章页码:2725 - 2744
Key words:overlapping stenosed artery; nanofluid; Grashof number; Brownian motion; thermophoresis; pharmacology
Abstract: This work is concerned with the analysis of blood flow through inclined catheterized arteries having a balloon (angioplasty) with time-variant overlapping stenosis. The nature of blood in small arteries is analyzed mathematically by considering it as a Carreau nanofluid. The highly nonlinear momentum equations of nanofluid model are simplified by considering the mild stenosis case. The formulated problem is solved by a homotopy perturbation expansion in terms of a variant of the Weissenberg number to obtain explicit forms for the axial velocity, the stream function, the pressure gradient, the resistance impedance and the wall shear stress distribution. These solutions depend on the Brownian motion number, thermophoresis number, local temperature Grashof number Gr and local nanoparticle Grashof number Br. The results were also studied for various values of the physical parameters, such as the Weissenberg number Wi, the power law index n, the taper angle f, the maximum height of stenosis δ*, the angle of inclination α, the maximum height of balloon σ*, the axial displacement of the balloon the flow rate F and the Froud number Fr. The obtained results show that the transmission of axial velocity curves through a Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0) is substantially lower than that through a Carreau nanofluid near the wall of balloon while the inverse occurs in the region between the balloon and stenosis. The streamlines have a clearly distinguished shifting toward the stenotic region and this shifting appears near the wall of the balloon, while it has almost disappeared near the stenotic wall and the trapping bolus in the case of horizontal arteries and Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0) does not appear but for the case of Carreau nanofluid bolus appears.
Cite this article as: Ashfaq Ahmed, Sohail Nadeem. Biomathematical study of time dependent flow of a Carreau nanofluid through inclined catheterized arteries with overlapping stenosis [J]. Journal of Central South University, 2017, 24(11): 2725–2744. DOI:https://doi.org/10.1007/s11771-017-3685-4.
J. Cent. South Univ. (2017) 24: 2725-2744
DOI: https://doi.org/10.1007/s11771-017-3685-4

Ashfaq Ahmed, Sohail Nadeem
Department of Mathematics, Quaid-I-Azam University, Islamabad 45320, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract: This work is concerned with the analysis of blood flow through inclined catheterized arteries having a balloon (angioplasty) with time-variant overlapping stenosis. The nature of blood in small arteries is analyzed mathematically by considering it as a Carreau nanofluid. The highly nonlinear momentum equations of nanofluid model are simplified by considering the mild stenosis case. The formulated problem is solved by a homotopy perturbation expansion in terms of a variant of the Weissenberg number to obtain explicit forms for the axial velocity, the stream function, the pressure gradient, the resistance impedance and the wall shear stress distribution. These solutions depend on the Brownian motion number, thermophoresis number, local temperature Grashof number Gr and local nanoparticle Grashof number Br. The results were also studied for various values of the physical parameters, such as the Weissenberg number Wi, the power law index n, the taper angle f, the maximum height of stenosis δ*, the angle of inclination α, the maximum height of balloon σ*, the axial displacement of the balloon 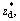 the flow rate F and the Froud number Fr. The obtained results show that the transmission of axial velocity curves through a Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0) is substantially lower than that through a Carreau nanofluid near the wall of balloon while the inverse occurs in the region between the balloon and stenosis. The streamlines have a clearly distinguished shifting toward the stenotic region and this shifting appears near the wall of the balloon, while it has almost disappeared near the stenotic wall and the trapping bolus in the case of horizontal arteries and Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0) does not appear but for the case of Carreau nanofluid bolus appears.
the flow rate F and the Froud number Fr. The obtained results show that the transmission of axial velocity curves through a Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0) is substantially lower than that through a Carreau nanofluid near the wall of balloon while the inverse occurs in the region between the balloon and stenosis. The streamlines have a clearly distinguished shifting toward the stenotic region and this shifting appears near the wall of the balloon, while it has almost disappeared near the stenotic wall and the trapping bolus in the case of horizontal arteries and Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0) does not appear but for the case of Carreau nanofluid bolus appears.
Key words: overlapping stenosed artery; nanofluid; Grashof number; Brownian motion; thermophoresis; pharmacology
1 Introduction
The study of blood flow through a stenosed artery is very important because of the fact that the cause and development of many cardiovascular diseases are related to the nature of blood movement and the mechanical behavior of the blood vessel walls. A stenosis is defined as a partial occlusion of the blood vessels due to the accumulation of cholesterol, fats and the abnormal growth of tissue. Cardiaccatheterization (also called heart catheterization) is a diagnostic procedure which does a comprehensive examination to determine how the heart and its blood vessels function. One or more catheter is inserted through a peripheral blood vessel in the arm (antecubital artery or vein) or leg (femoral artery or vein) with X-ray guidance. This procedure gathers information such as adequacy of blood supply through the coronary arteries, blood pressure, blood flow throughout chambers of the heart, collection of blood samples, and x-rays of the heart’s ventricles or arteries [1]. The human arterial or vascular system is injected with a dye to determine any blockages, narrowing, or abnormalities in the coronary arteries. By using X-ray, any visible signs appear which assess the patient’s need and his readiness for surgery, or perhaps a less invasive approach, such as dilation of a narrowed blood vessel either surgically or with the use of a balloon (angioplasty). The important contributions of recent years to the topic are referenced in the literature [2–5]. Many of researches about atherosclerotic development indicate that the studies are mainly concerned with the single symmetric and non-symmetric stances while the sentences may develop into a series (multiple stenoses) or may be of irregular shapes or overlapping or of composite in nature. Some studies considered an overlapping stenosis in the blood vessel segment. CHAKRAVARTY and MANDAL [6] noted that the problem becomes more acute in the presence of an overlapping stenosis in the artery instead of a mild one. The effect of vessel tapering is another important factor that was considered. CHAKRAVARTY and MANDAL [7] formulated the problem on tapered blood vessel segment having an overlapping stenosis. ISMAIL et al [8] studied the power-law model of blood flow through an overlapping stenosed artery where an improved shape of the time-variant stenosis in the tapered arterial lumen is given and the vascular wall deformability is taken to be elastic (moving wall).LAYEK et al [9] investigated the effects of an overlapping stenosis on flow characteristics considering the pressure variation in both the radial and axial directions of the arterial segment under consideration. SRIVASTAVA et al [10] addressed the problem of blood flow through an overlapping stenosis assuming that the flowing blood is represented by a two-layered macroscopic two-phase model. NADEEM et al [11] were concerned with the analysis of blood through an annulus, bounded between an arterial stenosis and a uniform catheter. The nature of blood through coaxial tubes is considered as that of a nano viscous fluid. Recently, MEKHEIER et al [12] studied the effect of induced magnetic field on blood flow through an anisotropically tapered elastic arteries with overlapping stenosis in an annulus.
In all the above mentioned studies, horizontal blood carrying vessels were considered. However, it is well- known that many ducts in physiological systems are not horizontal but have any inclination to the axis. The force of gravity comes into the picture due to the consideration of inclined artery. VAJRAVELU et al [13] have studied the peristaltic transport of a Herschel-Bulkley fluid in an inclined tube. MARUTHI and RADHAKRISHNAMCHARYA [14] have proposed steady blood flow through an inclined nonuniform tube with multiple stenoses. NADEEM and AKBAR [15, 16] have discussed the peristaltic transport of Herschel- Bulkley fluid and Walter’s B fluid in a non-uniform inclined tube. PRASAD et al [17] have studied the Peristaltic transport of a micropolar fluid in an inclined tube under the assumptions of long wavelength and low Reynolds number. Recently, CHAKRABORTY et al [18] have studied the effects of slip (at the stenotic wall), hematocrit and inclination of the artery on the flow variables (wall shear stress, shear stress at the throat of the stenosis and resistance to flow) for blood flow through an inclined vessel with an axially non- symmetrical mildstenosis, taking into account that blood is represented by a particle-fluid suspension. Most of these studies do not study the effect of the catheter that have a balloon (angioplasty) on blood flow through inclined arteries with overlapping stenosis which occurs in many clinical applications. The majority of the literature deals with the flows of viscous fluid described by means of the classical Newtonian model. However, there are many rheological complex fluids such as polymeric liquids, drilling mud, paints, lubricating oils, biological fluids and so forth for which the classical Navier Stokes theory is inadequate. The study of such fluids has gained much interest in recent years because of their numerous industrial and technological applications. Such fluids are often referred to as non-Newtonian fluids. Typical non-Newtonian flow characteristics include shear thinning, shear-thickening, viscoelasticity, viscoplasticity and so forth. For the flows of non- Newtonian fluids, there is not a single model that describes all of their properties as is done for the Newtonian fluid. The flows of such fluids can be analyzed with the help of a power-law model. However, now in addition to viscosity, another parameter, namely the power-law index (or exponent) used to characterize the flows of such fluids can be analyzed with the help of a power-law model KHAN et al [19]. In this work, our concern is on a four parameter model that does not have a discontinuous first derivative, which is known as Carreau model. The Carreau fluid displays (shear- thinning) that the viscosity decreases with increasing shear rate, sometimes reaching 10–3 or 10–4 for a zero-shear rate. We introduce nanoparticles to the base fluid (Carreau fluid). This factor is often the most important property for engineering calculations BUONGIORNO [20] as well as biological application point of view. Nanofluids are the fluid of nanometer- sized particles of metals, oxides, carbides, or nanotubes. Nowadays, nanofluids among researchers, are considered an active area of research. In fact, nanofluids are a suspension of nanosized solid particles in a base fluid. The nanofluids have high thermal conductivity as compared to the fluid. Nanofluids basically increase heat transfer rate as reported by NADEEM and AKBAR [21], NADEEM and LEE [22], AKBAR et al [23], NADEEM et al [24], ELLAHI et al [25, 26], JAYARAMAN and SARKAR [27], AHMED and NADEEM [28] and HAYAT et al [29].
With the above discussion in mind, the goal of this investigation is to study the effect of the catheter that has a balloon (angioplasty) on the flow of Carreau nanofluid (as a blood model) through inclined arteries with time-variant overlapping stenosis. The problem is first modeled and the non-dimensional governing equations are formulated. The non-dimensional governing equations in the case of mild stenosis and the corresponding boundary conditions are prescribed then solved analytically. The results for the resistance impedance, wall shear stress distribution, the axialvelocity, the pressure gradient has been discussed for various values of the problem parameters. Also the contour plots for the stream function are discussed. Finally, the main finding of the results is summarized as concluding remarks.
2 Mathematical model
Consider an incompressible Carreau nanofluid of viscosity μ and density flowing through coaxial tubes such that the inner tube r represents catheter having a balloon (angioplasty) on its wall and assumed that the balloon model is axi-symmetric in nature while the outer tube having a finite length L with overlapping stenosis and inclined at an angle α to the horizontal. Let (r, θ, z) be the coordinates of a material point in the cylindrical polar coordinate system where z-axis is taken along the axis of the artery while r is taken along the radial and circumferential directions respectively. Further, we assume that r=0 is chosen as the axis of the symmetry of the coaxial tubes. The geometry of the arterial wall with time-variant overlapping stenosis and the balloon model are defined by the functions R(z, t) and h(z), respectively, as in Fig. 1 can be written mathematically as [8–19]:
 (1)
(1)

Fig. 1 Schematic diagram of catheterized overlapping stenosed artery
The time-variant parameter Ω(t) is taken to be
 (2)
(2)
The balloon model is as
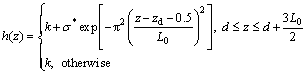 (3)
(3)
where R0 is the constant radius of the normal artery in the non-stenotic region, f is the angle of tapering, 3L0/2 is the length of overlapping stenosis, d is the location of the stenosis, δcosf is taken to be the critical height of the overlapping stenosis, m=tanf represents the slop of the tapered arteries, ε is a constant, ω represents the angular frequency of the forced oscillation and t is the time, σ denotes the maximum height attained by the balloon at z=zd+0.5, R0 is the radius of the inner tube which keeps the balloon in position, k<<1 and zd represents the axial displacement of the balloon. We can explore the possibility of different shapes of the artery viz, the converging tapering (φ<0), non-tapered artery (f=0) and the diverging tapering (f>0) [30].
The governing equations for conservation of mass, momentum, thermal energy and nanoparticles fraction [20]:
 (4)
(4)
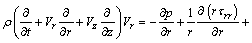
 (5)
(5)
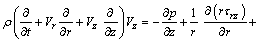
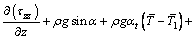
 (6)
(6)
The energy equation is
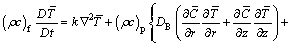
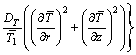 (7)
(7)
The mass concentration equation is
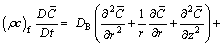
 (8)
(8)
where p is the fluid pressure, Vr and Vz are the velocity components in radial and axial directions respectively, g is the acceleration due to gravity and α is the angle of inclination. In Eqs. (7) and (8), 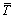 and
and  , represent the nanoparticle phenomenon, DB is the Brownian diffusion coefficient of diffusivity, Cp is the thermophoretic diffusion coefficient, ρf is the density of base fluid, ρp is the density of the nanoparticles.
, represent the nanoparticle phenomenon, DB is the Brownian diffusion coefficient of diffusivity, Cp is the thermophoretic diffusion coefficient, ρf is the density of base fluid, ρp is the density of the nanoparticles. 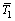 and
and 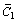 are the free stream temperature as r tends to R, Cp is the specific heat at constant pressure.
are the free stream temperature as r tends to R, Cp is the specific heat at constant pressure.
The extra stress tensor for Carreau fluid is defined by ABD et al [31],
 (9)
(9)
where τij, i, j=r, θ, z are the components of extra stress tensor, η∞ is the infinite shear rate viscosity, η0 is the zero shear rate viscosity, Γ is the time constant, n is the dimensionless power law index and  is the shear rate defined as
is the shear rate defined as
 (10)
(10)
where Π is the second invariant of the strain rate tensor 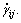 According to BIRD et al [32] and TANNER [33], we consider the case in which η∞ and
According to BIRD et al [32] and TANNER [33], we consider the case in which η∞ and  [14], so, we can write the components of the extra stress tensor as
[14], so, we can write the components of the extra stress tensor as
 (11)
(11)
The boundary conditions are:
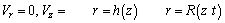 (12)
(12)
We introduce the following non-dimensional variables:

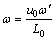 (13)
(13)
In the above equations, Wi is the Weissenberg number, Re is the Reynolds number, E=Fr/R0 is the dimensionless quantity, Fr is the Froud number and u0 is the velocity averaged over the section of the tube with radius R0. We non-dimenssionalize Eqs. (4)–(9) by using Eq. (11) to find the appropriate equations describing the flow of Carreau fluid in the case of a mild stenosis (δ*=δ/R0), subject to the additional condition
 [34] after dropping the dashes as
[34] after dropping the dashes as
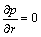 (14)
(14)

 (15)
(15)
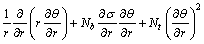 (16)
(16)
 (17)
(17)
In the above equations, Nt, Nb, Br, Gr are defined thermopheresis parameter, Brownian motion parameter, local nanoparticle Grashof number, and as local temperature Grashof number, respectively.
The boundary conditions are defined as follows:
 (18)
(18)
 (19)
(19)
 (20)
(20)
With
 (21)
(21)
and
 (22)
(22)
Here


3 Solution developments
We apply HPM to solve Eqs. (15)–(17) as follows [26–29, 35]:


 (23)
(23)
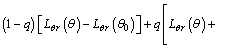
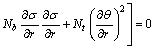 (24)
(24)

 (25)
(25)
Operators and initial guesses are defined as

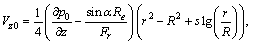
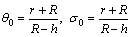
According to HPM, we can decompose the unknown variables as follows:
 (26)
(26)
After the straight forward calculations the solutions of the axial velocity, energy equation, mass concentration and the pressure gradient together with the corresponding boundary conditions will be in the forms and q→1, we have
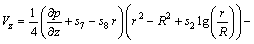

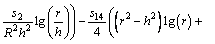
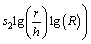 (27)
(27)

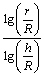 (28)
(28)
 (29)
(29)
The corresponding stream function ( with ψ=0 at r=h) is
with ψ=0 at r=h) is
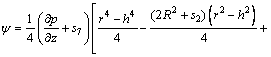

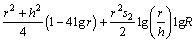 (30)
(30)
where


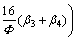 (31)
(31)
Using Eq. (27), we can find the expression for the wall shear stress in the form:
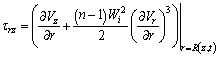 (32)
(32)
Since the flow rate F is constant for all the sections of the tube. The pressure drop across the length of the overlapping stenosis is
 (33)
(33)
The resistance to flow (resistance impedance) experienced by the flowing blood in the arterial segment under consideration using Eq. (24) may be defined as

 (34)
(34)
where 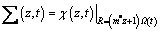 and h=k.
and h=k.
4 Graphical results and discussion
Computer codes are developed to evaluate the analytic results obtained for the axial velocity Vz, the resistance impedance λ and the wall shear stress distribution τrz. In order to discuss the results obtained from Eqs. (27), (32) and (34) quantitatively, we use the following experimental data ISMAIL [8]:
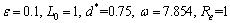
According to BIRD et al [32] and TANNER [33], the values of various parameters for Carreau fluid are n=0.398, 0.496 and Γ=1.04, 1.58. Weissenberg number physically means that the viscosity decreases as Wi is increased and it is directly proportional to relaxation time with constant of averaged velocity over the section of the tube and the radius of the tube. It is noted that (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0), then the fluid will become Newtonian fluid.
Figures 2(a) and (b) describe the distribution of the axial velocity Vz for different values of Weissenberg number Wi and power law index n, for various values of the parameters: t=0.5, z=1.2, δ*=0.1, σ*=0.2, f=0,Fr=0.08, Fr=0.08, F=0.5, α=15°, 
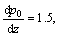 k=0.01, Gr=0.9, Br=0.7, Nt=0.8, Nb=0.5 under n=0.398, Wi=0, 0.4, 0.8 and Wi=0.8, n=0.398, 0.496, 1.
k=0.01, Gr=0.9, Br=0.7, Nt=0.8, Nb=0.5 under n=0.398, Wi=0, 0.4, 0.8 and Wi=0.8, n=0.398, 0.496, 1.

Fig. 2 Variation velocity profiles Vz for different values of Weissenberg number Wi (a) and power law index n (b)
It is observed that the axial velocity increases by increasing the Weissenberg number Wi, while it decreases with increasing the power law index n in the region (0.09
Figures 3(a) and (b) are prepared to see the effects of f and F on the axial velocity for various values of the parameters:
t=0.5, z=0.2, δ*=0.1, k=0.01, Wi=0.1, n=0.398, α=15°, Fr=0.1,  Gr=0.2, Br=0.2, Nt=0.3, Nb=0.03 under f=0, F=0.3, 0.5, 0.6 and F=0.3, f=0, 0.05, –0.05.
Gr=0.2, Br=0.2, Nt=0.3, Nb=0.03 under f=0, F=0.3, 0.5, 0.6 and F=0.3, f=0, 0.05, –0.05.

Fig. 3 Variation velocity profiles Vz for different values of tapered angle f (a) and flow rate F (b)
The effects of vessel tapering together with the shape of stenosis on the blood flow characteristics seem to be equally important and hence deserve attention. The tapering is a significant aspect of the mammalian arterial system. Thus, in this work, we are interested in the flow through a tapered artery f=–0.05 are higher than those in the non-tapered artery f=0 and the diverging tapered artery f=0.05 in the region 0.1 The effects of the angle of inclination α and Froud number Fr on the axial velocity Vz are displayed in Figs. 4(a) and (b). To discuss these effects we use the following data: t=0.5, z=0.2, δ*=0.1, σ*=0.2, Wi=0.1, f=0, F=0.2, It is noted that the axial velocity increases by increasing the angle of inclination α while it decreases with increasing the Froud number Fr in the region (0.1 Fig. 4 Variation velocity profiles Vz for different values angle of inclination α (a) and Froud number Fr (b) Figures 5(a) and (b) are established for the variation of thermopheresis parameter (Nt) and Brownian motion parameter (Nb) for various parameters: t=0.5, z=0.2, δ*=0.1, σ*=0.2, Wi=0.1, α=15°, Fr=0.1, f=0, F=0.2, It is observed that the axial velocity decreases with increasing the thermopheresis parameter (Nt) in the region (0.1 t=0.5, α=45°, Fr=0.1, F=0.1, Wi=0.1, n=0.398, Fig. 5 Variation velocity profiles Vz for different values angle of variation of thermopheresis parameter Nt (a) and Brownian motion parameter Nb (b) It is observed that the wall shear distribution decreases by increasing the maximum height of stenosis δ* and the maximum height of balloon σ* also the magnitude of the wall shear stress distribution is higher in the case of non-stenosis δ*=0 uniform tube than that of the case of stenosis. Figures 7(a) and (b) shows the axial displacement of the balloon Fig. 6 Variation of wall shear stress distribution τrz with z for different values of maximum height of stenosis of δ* (a) and maximum height of balloon σ* (b) Fig. 7 Variation of wall shear stress distribution τrz with z for different values of axial displacement of the balloon We can record that by increasing the axial displacement of the balloon Figures 8(a) and (b) illustrate the variation of the wall shear stress distribution τrz in the stenotic region for different values of the angle of inclination α and Froud number Fr. To see the effects of α and Fr on the wall shear stress, we prepared Figs. 8(a) and (b) with the parameters: t=0.5, z=0.2, δ*=0.1, σ*=0.2, Wi=0.1, n=0.398, f=0, F=0.2, Fig. 8 Variation of wall shear stress distribution τrz with z for different values of angle of inclination α (a) and Froud number Fr (b) It is note that the wall shear stress distribution decreases by increasing the angle of inclination α while it is increased by increasing the Froud number Fr in the region (1.05≤z≤1.93) and the opposite direction occurs in the regions (0.75≤z≤1.05) and (1.93≤z≤2.25), also curves through the horizontal tube α=0° are higher than those in the inclined tube α=45° and the vertical tube α=90° in the region (1.05≤z≤1.93) and the inverse occurs in the regions (0.75≤z≤1.05) and (1.93≤z≤2.25). The variation of the wall shear stress distribution τrz in the stenotic region for different values of Weissenbergnumber Wi and power law index n is displayed in the Figs. 9(a) and (b) by using the following data: t=0.5, z=1.2, δ*=0.1, σ*=0.2, f=0, Fr=0.08, Fr=0.08, F=0.5, α=15°, Fig. 9 Variation of wall shear stress distribution τrz with z for different values of Weissenberg number Wi (a) and power law index n (b) It is observed that wall shear stress distribution increases by increasing the Weissenberg number Wi while it decreases with increasing the power law index n and transmission of the wall shear stress curves through a Newtonian fluid Wi=0, n=1 is substantially higher than that through a Carreau Nanofluid. Figures 10(a) and (b) show the wall shear stress distribution τrz in the stenotic region for different values of thermopheresis parameter (Nt) and Brownian motion parameter (Nb) for various values of the parameters:t=0.5, z=1.2, δ*=0.1, σ*=0.2, Wi=0.01, n=0.398, f=0, F=0.3, Fig. 10 Variation of wall shear stress distribution τrz with z for different values of thermopheresis parameter Nt (a) and Brownian motion parameter Nb (b) It is obvious that by increasing the values of Nt the wall shear stress decreases and the wall shear stress increases by increasing the values of Nb, also, we can observe that for higher values of Brownian motion parameter Nb there is a slight change in the wall shear stress is being recorded. Figures 11(a) and (b) illustrate the variation of resistance to flow or resistance to impedance with maximum height of stenosis δ* for different values of the maximum height of the of balloon σ* and tapered angle f. To see the effects of σ* and f on resistance impedance, we prepared Figs. 11(a) and (b) with the data: t=0.5, z=0.2, δ*=0.1, σ*=0.2, k=0.01, Wi=0.1, n=0.398, α=15°, Fr=0.1, F=0.1, It is observed that the resistance impedance increases by increasing σ* and the magnitude of the resistance impedance is higher in the case of catheter having a balloon σ*≠0 than that for the case of uniform catheter σ*=0, also the curves through the converging tapered artery f=–0.05 are higher than those in the non-tapered artery f=0 and diverging tapered artery f=0.05. Fig. 11 Variation of resistance to flow or resistance to impedance λ with maximum height of stenosis δ* for different values of the maximum height of the balloon σ* and tapered angle f (Panels (a) and (b) respectively) Figures 12(a) and (b) are developed for the variation of resistance impedance to flow or resistance impedance λ for different values of the angle of inclination α and Froud number Fr by holding other values of the parameters:t=0.5, z=0.2, δ*=0.1, σ*=0.2, Wi=0.1, n=0.398, f=0, F=0.2, It is observed that the resistance impedance decreases with increasing the angle of inclination α, these results agree closely with those of VAJRAVELU et al [13], NADEEM and AKBAR [15] and CHAKRABORTY et al [18]. The magnitude of resistance impedance increases by increasing the Froud number Fr while it decreases as the acceleration due to gravity g increases also increasing the values of Froud number Fr gradually, the effect of gravity on resistance impedance is very small. Moreover, the curves through horizontal tube α=0° are higher than those in the inclined tube α=45° and vertical tube α=90°. Fig. 12 Variation of resistance to flow or resistance to impedance λ with maximum height of stenosis δ* for different values of the angle of inclination α (a) and Froud number Fr (b) Figures 13(a) and (b) are made to investigate the influence of thermopheresis effects and Brownian motion effects on the resistance impedance, we prepared the Figs. 13(a) and (b) for the following values of parameters:t=0.5, z=1.2, δ*=0.1, σ*=0.2, Wi=0.2, n=0.398, f=0, F=0.9, Fig. 13 Variation of resistance to flow or resistance to impedance λ with maximum height of stenosis δ* for different values of thermopheresis effects (a) and Brownian motion effects (b) Figures 14(a) and (b) are prepared to judge the variation in the resistance impedance of the following data:t=0.5, z=1.2, δ*=0.1, σ*=0.2, f=0, Fr=0.1, F=0.1, α=15°, It is clear that the resistance impedance with the time t have a periodic oscillation form, we can record that the resistance impedance increases by increasing Wi and n, also the transmission of the resistance impedance curves through Carreau fluid is substantially higher than that through a Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0). Figures 15(a) and (b) are made to investigate the influence of thermopheresis effects and Brownian motion effects on the resistance impedance, we prepared Figs. 16(a) and (b) for the following values of parameters:t=0.5, z=1.2, δ*=0.1, σ*=0.2, f=0, Wi=0.2, n=0.398, Fr=0.08, Fr=0.1, F=0.1, α=15°, Fig. 14 Variation of resistance to flow or resistance to impedance λ with t for different values of Weissenberg number Wi (a) and power law index n (b) Fig. 15 Variation of resistance to flow or resistance to impedance λ with t for different values of thermopheresis effects (a) and Brownian motion effects (b) Fig. 16 Variation of temperature profile for different values of thermopheresis effects (a) and Brownian motion effects (b) It is clear that the resistance impedance with the time t have a periodic oscillation form, we can observe that the resistance impedance increases by increasing in thermopheresis parameter Nt. While for the case of Brownian motion parameter Nb, when the random motion of particles increases then the resistance impedance decreases. Table 1 shows the absolute error for various values of the physical parameters, such as the Weissenberg number Wi, the power index n, the taper angle f the maximum height of stenosis δ*, the angle of inclination α, the maximum height of balloon σ*, the axial displacement of the balloon Table 1 Computation of absolute error velocity profile Figures 16(a) and (b) illustrate the variation of temperature profile for the following data:t=0.5, z=1.2, δ*=0.1, σ*=0.2, f=0, It is clearly seen that the increase in thermopheresis parameter Nt the temperature will increase, but the case of increasing Brownian motion parameter Nb, the temperature is decreasing. Figures 17(a) and (b) illustrate the variation of the concentration profile for the same parameters as considered for temperature profile, showing a decrease in the concentration profile for the increment in thermopheresis parameter Nt, while an increase in the concentration profile for increasing the random Brownian motion. Trapping represents an interesting phenomenon for the fluid flow. This phenomenon gain more attracting in the presence of nanoparticles. In the wave frame, streamlines under certain conditions split to trap a bolus which movies as a whole with the speed of wave. The formation of internally circulating bolus of the fluid by closed streamlines is called trapping. The bolus defined as a volume of fluid bounded by a closed streamlines in the wave frame is transported at the wave. Figure 18 reveals that the size of tapping bolus increases by increasing the axial displacement of the balloon and the streamlines distinguished shifting towards the stenotic region (0.75≤z≤2.25), also at Fig. 17 Variation of concentration profile for different values of thermopheresis effects and Brownian motion effects (Panels (a) and (b) respectively) Fig. 18 Plot shows streamlines for different values of axial displacement of the balloon with Fig. 19 Plot showing different values of Weissenberg number with Wi=0 (a), Wi=0.03 (b), Wi=0.04 (c) Fig. 20 Plot showing different values of power law index with n=0.398 (a), n=0.496 (b) and n=1 (c) Fig. 21 Plot showing different values of angle of inclination with α=0°(a), α=45°(b), α=90°(c) Fig. 22 Plot showing different values of maximum height of balloon with σ=0.3 (a), σ=0.4 (b) and σ=0.5 (c) Fig. 23 Plot showing different values of thermopheresis parameter Nt with Nt=0.7 (a), Nt=0.8 (b) and Nt=0.9 (c) Fig. 24 Plot showing different values of Brownian motion parameter Nb with Nb=0.1 (a), Nb=0.2 (b) and Nb=0.3 (c) 5 Concluding remarks The effects of the catheter that have a balloon (angioplasty) on the flow of Carreau nanofluid as a blood model through inclined artery with time-variant overlapping stenosis is studied. Graphical results are presented for the wall shear stress distribution and resistance to flow (resistance impedance), axial velocity and trapping. The main finding can be summarized as follows: 1) The transmission of axial velocity curves through a Newtonian fluid is substantially lower than that through a Carreau nanofluid near the wall of balloon while the inverse occurs in the region between the balloon and stenosis. 2) The magnitude of the axial velocity increases clearly by increasing the acceleration due to gravity and the curves through the vertical tube α=90° is higher than those in the inclined tube α=45° and horizontal tube α=0° near the wall of the balloon while the inverse occurs in the region between the balloon and stenosis. 3) The effects of the gravity on the axial velocity and resistance impedance is very negligible small by increasing the values of Froud number gradually. 4) Under stenotic conditions, the curves of axial velocity and resistance impedance through the converging tapered artery are higher than those in the non-tapered artery and the diverging tapered artery while the curves of the wall shear stress have an inverse behavior. 5) The resistance to flow decreases, but the wall shear stress distribution in the stenotic region increases with the inclination of the tube these results agree closely with the VAJRAVELU et al [13], Nedeem and Noreen Sher Akber [15] and Uday Shankar Chakraborty et al [18]. 6) The resistance impedance profiles with the time have an oscillation form through tapered overlapping stenosed arteries and this oscillation decaying as the time progresses. 7) The streamlines have a clearly distinguished shifting towards the stenotic region and this shifting appear near the wall of the balloon, while it have almost disappeared near the stenotic wall. 8) The size of the trapping bolus through the vertical tube α=90° are smaller than those in the inclined tube α=45° and the horizontal tube α=0°. 9) The trapping bolus in the case of horizontal artery α=0° and Newtonian fluid (Wi=0, n=1, Gr=0, Br=0, Nt=0, Nb≠0) disappears. Appendix References [1] MEKHEIMER K H, ELKOT M A. Influence of magnetic field and Hall currents on blood flow through stenotic artery [J]. App Math Mech Engl Ed, 2008, 29: 1093–1104. [2] MEKHEIMER K H, ELKOT M A. The micropolar fluid model for blood flow through a tapered arteries with a stenosis [J]. Acta Mech Sin, 2008, 24: 637–644. [3] MEKHEIMER K H, ELKOT M A. Suspension model for blood flow through arterial catheterization [J]. Chem Eng Comm, 2010, 197: 1–20. [4] MEKHEIMER K H, HAROUN M H. Effects of magnetic field, porosity, and wall properties for anisotropically elastic multi-stenosis arteries on blood flow characteristics [J]. App Math Mech Engl Ed, 2011, 32: 1047–1064. [5] MEKHEIMER K H, ELKOT M A. Mathematical modeling of axial flow between two eccentric cylinders: Application on the injection of eccentric catheter through stenotic arteries [J]. International Journal of Non-Linear Mechanics, 2012, 47: 927–937. [6] CHAKRAVARTY S, MANDAL P K. A nonlinear two-dimensional model of blood flow in an overlapping arterial stenosis subjected to body acceleration [J]. Mathematical and Computer Modelling, 1996, 24: 43–58. [7] CHAKRAVARTY S, MANDAL P K. Two-dimensional blood flows through tapered arteries under stenotic conditions [J]. International Journal of Non-Linear Mechanics, 2000, 35: 779–793. [8] ISMAIL Z, ABDULLAH, MUSTAPHA I N, AMIN N A. Power-law model of blood flow through a tapered overlapping stenosed artery [J]. Appl Math and Comp, 2008, 195: 669–680. [9] LAYEK G C, MUKHOPADHYAY S, GORLA R S D. Unsteady viscous flow with variable viscosity in a vascular tube with an overlapping constriction [J]. International Journal of Engineering Science, 2009, 47: 649–659. [10] SRIVASTAVA V P, RASTOGI R. Blood flow through stenosed catheterized artery: Effects of hematocrit and stenosis shape [J]. Comput Math Applc, 2010, 59: 1377–1785. [11] NADEEM S, IJAZ S. Nanoparticles analysis on the blood flow through a tapered catheterized elastic artery with overlapping stenosis [J]. The European Physical Journal Plus, 2014, 129: 249–262. [12] MEKHEIMER K H S, HAROUN M H, ELKOT M A. Induced magnetic field influences on blood flow through an anisotropically tapered elastic arteries with overlapping stenosis in an annulus [J]. Can J Phys, 2011, 89: 201–212. [13] VAJRAVELU K, SREENADH S, RAMESH B V. Peristaltic transport of a Herschel bulkley fluid in an inclined tube [J]. Int J Non-linear Mech, 2005, 40: 83–90. [14] MARUTHI P K, RADHAKRISHNAMACHARYA G. Flow of herschel-bulkley fluid through an inclined tube of non-uniform cross-section with multiple stenoses [J]. Arch Mech, 2008, 60: 161–172. [15] NADEEM S, AKBAR N S. Influence of heat transfer on a peristaltic transport of Herschel-Bulkley fluid in a non-uniform inclined tube [J]. Commun Nonlinear SciNumer Simulat, 2009, 14: 4100–4113. [16] NADEEM S, AKBAR N S. Peristaltic flow of Walter’s B fluid in a uniform inclined tube [J]. J Biorheol, 2010, 24: 22–28. [17] PRASAD K M, RADHAKRISHNAMACHARYA G, MURTHY J V. Peristaltic pumping of a micropolar fluid in an inclined tube’ [J]. Int J of Appl Math and Mech, 2010, 6: 26–40. [18] CHAKRABORTY U S, DEVAJYOTI B, MOUMITA P. Suspension model blood flow through an inclined tube with an axially non-symmetrical stenosis [J]. Korea Australia Rheology Journal, 2011, 23: 25–32. [19] KHAN M, ABBAS Q, DURUK. Magnetohydrodynamic flow of a Sisko fluid in annular pipe: A numerical study [J]. Int J Numer Meth Fluids, 2010, 62: 1169–1180. [20] BUONGIORNO J. Convective transport in nanofluids [J]. ASME J Heat Transfer, 2006, 128: 240–250. [21] NADEEM S, AKBAR N S. Jeffrey fluid model for blood flow through atapered artery with a stenosis [J]. J Mech Med Biol, 2011, 11: 529–545. [22] NADEEM S, LEE C. Boundary layer flow of nanofluid over an exponentially stretching surface’ [J]. Nanoscale Res Lett, 2012,7: 94–99. [23] AKBAR N S, NADEEM S, HAYAT T, HENDI A. Peristaltic flow of a nanofluid with slip effects [J]. Meccanica, 2012, 47(5): 1283–1294. [24] NADEEM S, IJAZS, AKBAR N S. Nanoparticle analysis for blood flow of Prandtl fluid model with stenosis [J]. Int Nano Letters, 2013, 3:35. [25] ELLAHI R, RAHMAN S U, NADEEMS, AKBAR N S. Blood flow of nanofluid through an artery with composite stenosis and permeable walls [J]. Appl Nanosci, 2014, 4(8): 919–926. [26] ELLAHI R. The thermodynamics, stability, applications and techniques of differential type: A review [J]. Reviews in Theoretical Science, 2014, 2(8): 116–123. [27] JAYARAMAN G, SARKAR A. Nonlinear analysis of arterial blood flow-steady streaming effect [J]. Nonlinear Analysis, 2005, 63: 880–890. [28] AHMED A, NADEEM S. Effects of magnetohydrodynamics and hybrid nanoparticles on a micropolar fluid with 6-types of stenosis [J]. Results in Physics, 2017, 7: 4130–4139. [29] HAYAT T, MUHAMMAD T, SHEHZAD S A, ALSAEDI A. Similarity solution to three dimensional boundary layer flow of second grade nanofluid past a stretching surface with thermal radiation and heat source/sink [J]. AIP Advances, 2015, 17(5): 017107–17. [30] MANDAL P K. Unsteady analysis of non-Newtonian blood flow through tapered arteries with a stenosis [J]. International Journal of Non-linear Mechanics, 2005, 40: 151–164. [31] ABD E N, ABD E H, MISIERY A E M. Effects of an endoscope and generalized Newtonian fluid on peristaltic motion [J]. Appl Math and Comput, 2002, 128: 19–35. [32] BIRD R B, ARMSTRONG R C, HASSAGER O. Dynamics of polymeric liquids. Fluid Mechanics [M]. New York: Wiley, 1977. [33] TANNER R I. Engineering Rheology [M]. New York: Oxford University Press, 1985. [34] YOUNG D F. Effect of a time dependent stenosis of flow through a tube’ [J]. J Eng Ind, 1968, 90(17): 248–254. [35] HE J H. Homotopy perturbation technique, a nonlinear analytical technique [J]. Comput Methods Appl, 2012, 135: 73–79. (Edited by HE Yun-bin) Cite this article as: Ashfaq Ahmed, Sohail Nadeem. Biomathematical study of time dependent flow of a Carreau nanofluid through inclined catheterized arteries with overlapping stenosis [J]. Journal of Central South University, 2017, 24(11): 2725–2744. DOI:https://doi.org/10.1007/s11771-017-3685-4. Received date: 2015-09-17; Accepted date: 2016-06-11 Corresponding author: Ashfaq Ahmed, PhD, Associate Professor; E-mail: qafhsam@hotmail.com
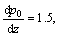 k=0.01, Gr=0.2, Br=0.2, under Fr=0.1, α=0°, 45°, 90° and α=15°, Fr=0.08, 0.1, 0.2.
k=0.01, Gr=0.2, Br=0.2, under Fr=0.1, α=0°, 45°, 90° and α=15°, Fr=0.08, 0.1, 0.2.

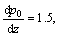 k=0.01, Gr=0.2, Br=0.2, under Nb=0.01, Nt=0.1, 0.2, 0.3, and Nt=0.1, Nb=0.01, 0.02, 0.03.
k=0.01, Gr=0.2, Br=0.2, under Nb=0.01, Nt=0.1, 0.2, 0.3, and Nt=0.1, Nb=0.01, 0.02, 0.03.
 k=0.05, Gr=0.1, Br=0.1, Nt=0.1, Nb=0.1 under σ*=0, δ*=0.05, 0.1, 0.15 and δ*=0, σ*=0.1, 0.2, 0.3.
k=0.05, Gr=0.1, Br=0.1, Nt=0.1, Nb=0.1 under σ*=0, δ*=0.05, 0.1, 0.15 and δ*=0, σ*=0.1, 0.2, 0.3.
 and taper angle f. By using the following parameters:t=0.5, α=45°, Fr=0.1, F=0.1, Wi=0.1, n=0.398,
and taper angle f. By using the following parameters:t=0.5, α=45°, Fr=0.1, F=0.1, Wi=0.1, n=0.398, k=0.05, σ*=0.2, δ*=0.1, Gr=0.1, Br=0.1, Nt=0.1, Nb=0.1 under f=0,
k=0.05, σ*=0.2, δ*=0.1, Gr=0.1, Br=0.1, Nt=0.1, Nb=0.1 under f=0,  0.2, 0.4 and
0.2, 0.4 and  f=0, 0.05, –0.05.
f=0, 0.05, –0.05.

 (a) and taper angle f (b)
(a) and taper angle f (b)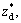 the curves shifts towards the left and the magnitude of the wall shear stress distribution decreases. It is also observed that the curves through the diverging tapered artery α=90° are higher than those in the non-tapered artery f=0 and the converging artery f=–0.05.
the curves shifts towards the left and the magnitude of the wall shear stress distribution decreases. It is also observed that the curves through the diverging tapered artery α=90° are higher than those in the non-tapered artery f=0 and the converging artery f=–0.05.
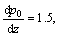 k=0.05, Gr=0.2, Br=0.2, Nt=0.1, Nb=0.1 under Fr=0.1, α=0°, 45°, 90° and α=45°, Fr=0.08, 0.1, 0.15, 0.2.
k=0.05, Gr=0.2, Br=0.2, Nt=0.1, Nb=0.1 under Fr=0.1, α=0°, 45°, 90° and α=45°, Fr=0.08, 0.1, 0.15, 0.2.

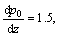 k=0.01, Gr=0.9, Br=0.7, Nt=0.8, Nb=0.5 under n=0.398, Wi=0, 0.1, 0.2 and Wi=0.8, n=0.398, 0.496, 1.
k=0.01, Gr=0.9, Br=0.7, Nt=0.8, Nb=0.5 under n=0.398, Wi=0, 0.1, 0.2 and Wi=0.8, n=0.398, 0.496, 1.
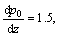 k=0.05, Gr=0.2, Br=0.2, α=45°, Fr=0.1, F=0.5 under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.1, Nb=0.01, 0.02, 0.1.
k=0.05, Gr=0.2, Br=0.2, α=45°, Fr=0.1, F=0.5 under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.1, Nb=0.01, 0.02, 0.1.
 Gr=0.2, Br=0.2, Nt=0.3, Nb=0.03 under f=0, σ*=0, 0.1, 0.2 and σ*=0.3, f=0, 0.05, –0.05.
Gr=0.2, Br=0.2, Nt=0.3, Nb=0.03 under f=0, σ*=0, 0.1, 0.2 and σ*=0.3, f=0, 0.05, –0.05.

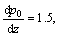 k=0.01, Gr=0.2, Br=0.2, Nt=0.3, Nb=0.03 under Fr=0.1, α=0°, 45°, 90°), (α=45°, Fr=0.1, 0.2, 0.3.
k=0.01, Gr=0.2, Br=0.2, Nt=0.3, Nb=0.03 under Fr=0.1, α=0°, 45°, 90°), (α=45°, Fr=0.1, 0.2, 0.3.

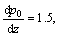 k=0.01, Gr=0.2, Br=0.2, α=15°, Fr=0.1, F=0.5 under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.3, Nb=0.01, 0.02, 0.03.We can observe that with the increase in thermopheresis parameter Nt there is an increase in the resistance impedance, we can also observe that there is a slight variation in the region (1.98≤δ*≤2.0). Furthermore, for the case of Brownian motion parameters (Nb), when the random motion of particles suspended in a fluid resulting from their collision increases, then the resistance impedance decreases. But with higher collisions of particles, the resistance impedance experiences the sight change and at the maximum values of the height of stenosis δ*, the resistance impedance shows no significant variation.
k=0.01, Gr=0.2, Br=0.2, α=15°, Fr=0.1, F=0.5 under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.3, Nb=0.01, 0.02, 0.03.We can observe that with the increase in thermopheresis parameter Nt there is an increase in the resistance impedance, we can also observe that there is a slight variation in the region (1.98≤δ*≤2.0). Furthermore, for the case of Brownian motion parameters (Nb), when the random motion of particles suspended in a fluid resulting from their collision increases, then the resistance impedance decreases. But with higher collisions of particles, the resistance impedance experiences the sight change and at the maximum values of the height of stenosis δ*, the resistance impedance shows no significant variation.

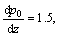 k=0.01, Gr=0.2, Br=0.2 under n=0.398, Wi=0, 0.1, 0.2 and Wi=0.1, n=0.398, 0.496m 1.
k=0.01, Gr=0.2, Br=0.2 under n=0.398, Wi=0, 0.1, 0.2 and Wi=0.1, n=0.398, 0.496m 1.
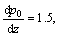 k=0.01, Gr=0.2, Br=0.2, under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.3, Nb=0.01, 0.02, 0.03.
k=0.01, Gr=0.2, Br=0.2, under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.3, Nb=0.01, 0.02, 0.03.


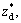 the flow rate F and the Froud number Fr.
the flow rate F and the Froud number Fr.
 k=0.01 under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.3, Nb=0.01, 0.02, 0.03.
k=0.01 under Nb=0.01, Nt=0.1, 0.2, 0.3 and Nt=0.3, Nb=0.01, 0.02, 0.03.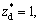 the balloon keeps its position at the stenotic region. This shifting appears near the wall of the balloon, while it has almost disappeared near the stenotic wall. The effects of Weissenberg number Wi and power law index n, the trapping are displayed in Figs. 19 and 20. It is clear that the size of the trapping bolus through the vertical tube (α=90°) are smaller than those in the inclined tube (α=45°) and the horizontal tube (α=0°) as depicted in Fig. 21. We can record that the size of trapping bolus decreases clearly by increasing the height balloon σ* as shown in Fig. 22. The sizes of trapping bolus are gradually becoming bigger when the thermopherosis parameter Nt has these quantities (Nt=0.7, 0.8, 0.9) as shown in the Fig. 23. The trapping bolus decreases greatly when the random motion of particles is faster under these quantities (Nb=0.1, 0.2, 0.3) as shown in Fig. 24. It is observed that the trapping appears clearly near the overlapping stenosis wall and the trapped bolus decreases in size as the Weissenberg number Wi increase while it is slightly increases in size by increasing the power law index n and trapping disappears for Newtonian fluid (n=1). Finally, we can see the size of bolus in the case of horizontal artery and Newtonian fluid disappears.
the balloon keeps its position at the stenotic region. This shifting appears near the wall of the balloon, while it has almost disappeared near the stenotic wall. The effects of Weissenberg number Wi and power law index n, the trapping are displayed in Figs. 19 and 20. It is clear that the size of the trapping bolus through the vertical tube (α=90°) are smaller than those in the inclined tube (α=45°) and the horizontal tube (α=0°) as depicted in Fig. 21. We can record that the size of trapping bolus decreases clearly by increasing the height balloon σ* as shown in Fig. 22. The sizes of trapping bolus are gradually becoming bigger when the thermopherosis parameter Nt has these quantities (Nt=0.7, 0.8, 0.9) as shown in the Fig. 23. The trapping bolus decreases greatly when the random motion of particles is faster under these quantities (Nb=0.1, 0.2, 0.3) as shown in Fig. 24. It is observed that the trapping appears clearly near the overlapping stenosis wall and the trapped bolus decreases in size as the Weissenberg number Wi increase while it is slightly increases in size by increasing the power law index n and trapping disappears for Newtonian fluid (n=1). Finally, we can see the size of bolus in the case of horizontal artery and Newtonian fluid disappears.

 0.8 (a),
0.8 (a),  0.9 (b),
0.9 (b),  1 (c)
1 (c)





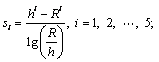
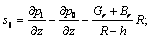




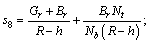


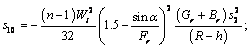
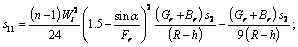
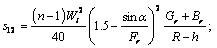
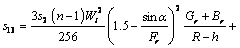


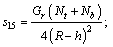
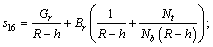

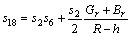 ;
;