双轴压缩下闭合裂纹应力强度因子的解析与数值方法

杨  慧¹，曹  平¹，江学良^{1, 2}，黄尚安³，黎振兹¹，许明情¹

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；

2. 湖南城市学院 土木工程学院，湖南 益阳，413000；

3. 中南大学 土木建筑学院，湖南 长沙，410083)

摘  要：采用“裂纹线应力场”分析方法，推导双轴压缩下有限岩板内闭合裂纹尖端应力强度因子的近似解析解，分析裂纹表面摩擦因数、侧压系数对裂尖应力强度因子的影响；运用有限元法对同一问题进行数值研究，并与解析解进行比较。研究结果表明：在岩体工程要求的精度之内，采用“裂纹线应力场”分析方法与有限元法这2种方法得出的结果基本吻合；裂纹长度a与岩板宽度W之比对裂纹尖端的应力强度因子有影响，按无限岩板情况计算裂纹尖端应力强度因子，其适用范围应有一定上限，即a/W≤0.2; 当a/W＞0.2时，应当考虑实际岩板的自由边界条件对裂纹尖端场的影响。

关键词：双轴压缩；有限岩板；闭合裂纹；应力强度因子；摩擦因数；侧压系数

中图分类号：O 319.56         文献标识码：A         文章编号：1672-7207(2008)04-0850-06

Analytical and numerical research of stress intensity factor with a closed-crack in finite-rock-plates under biaxial compression

YANG Hui¹, CAO Ping¹, JIANG Xue-liang^{1, 2}, HUANG Shang-an³, LI Zhen-zi¹, XU Ming-qing¹

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. School of Civil Engineering, Hunan City University, Yiyang 413000, China;

3. School of Civil and Architectural Engineering, Central South University, Changsha 410083, China)

Abstract: Model of closed-crack in finite-rock-plate under biaxial compression was established. Based on crack-line analysis method, the approximately solutions for the crack tip stress intensity factor(SIF) were deducted. The influences of friction coefficient and side pressure coefficient on crack tip stress intensity factor were analyzed. Using the finite element method, the numerical study was given to the same question. The results calculated by two methods are similar within the accuracy requirement in engineering. The ratio of crack length a and plate width W influence SIF. There exists an upper limit, i.e., a/W≤0.2. When a/W＞0.2 for the application of infinite-plate formula to calculate SIF, the rock-plate should be considered as finite-rock-plate and the influence of boundary conditions on crack tip should not be neglected.

Key words: biaxial compression; finite-rock-plate; closed-crack; stress intensity factor; friction coefficient; side pressure coefficient

双轴压缩断裂与双轴拉伸断裂有很大的区别。人们对双轴压缩下岩板内闭合裂纹进行了大量研究^[1-5]，但大都只限于无限板与远场加载的情况。究其原因可能是有限岩板闭合裂纹尖端应力强度因子的求解比较困难，从理论到实践尚有许多问题还未得到解决。然而，裂纹的长度与有限结构的尺寸之比对裂纹尖端的应力场、位移场有较大的影响，不能忽略，应当考虑实际板的自由边界对裂纹尖端场的影响。王静等^[6]利用“伪力法”和叠加原理给出了含中心斜裂纹的岩石类材料在压缩荷载作用下应力强度因子的解法，但认为闭合裂纹存在Ⅰ型裂纹应力强度因子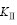，物理意义不明确。事实上，当裂纹受压闭合后，Ⅰ型应力分量的奇异性不复存在，此时，复合型裂纹转化为特殊的纯Ⅱ型裂纹^[7-11]。在此，本文作者采用裂纹线应力场分析方法，在文献[12]的基础上，给出双轴压缩下有限岩板闭合裂纹尖端应力强度因子的近似解析解（《应力强度因子手册》^[13]中尚无该问题的解答）。

1  解析研究

1.1  无限大板含闭合裂纹的应力强度因子计算

设在远场压应力σ₁和σ₃作用下，主裂纹面发生闭合，由于受摩擦力的影响，裂纹面间的有效剪应力为

将式(2)代入式(1)，则闭合裂纹面上的有效剪应力为

该有效剪应力使裂纹面产生相对滑动，由于裂纹已经闭合，闭合斜裂纹实质上是一种特殊的纯Ⅱ型裂纹，K₁ =0，即

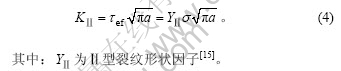
1.2  有限大板含闭合裂纹的应力强度因子计算

有限宽岩板双轴受压，裂纹闭合后的受力状态等价于裂纹表面自由、外边界承受有效剪应力作用的受力状态，如图1所示。因此，受压闭合后裂纹端部Ⅰ型应力强度因子恒为零，成为一种特殊的Ⅱ型裂纹^[16]。本文将采用线场分析方法，寻求问题的近似解析解。

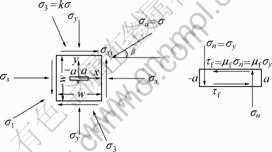
图1  闭合裂纹模型受双轴压缩荷载作用

Fig.1  Closed-crack model under multiaxial compression

无限大Ⅱ型中心裂纹如图2所示，其应力场的表达式可运用Westergaard应力函数表达

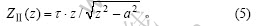
则应力分量表达式为

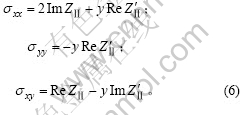
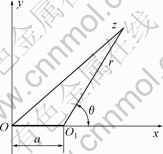
图2  闭合裂纹尖端示意图

Fig.2  Sketch map of closed-crack tip

将坐标原点移至裂纹尖端，以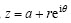代入式(6)，令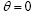即可得在裂纹线上的应力分量：

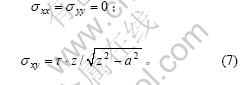
在求解宽度为W的有限岩板中心裂纹双向受压闭合后的应力强度因子时，裂纹尖端应力场较难得到，但在裂纹线附近却与(6)式有类似的形式，因而，认为在裂纹线上(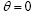)近似有

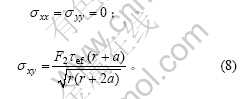
为了建立裂纹线上由静力平衡条件转化而来的边界条件，应有

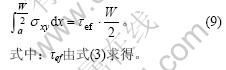
将式(8)代入(9)后，解出修正系数为

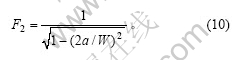
考虑不同的裂纹长度，得到对应的F₂，见表1。于是，可求得有限岩板闭合裂尖应力强度因子的解析表达式为

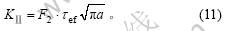
表1  应力强度因子修正系数F₂

Table 1  Value of modify coefficient F₂

由式(4)，(11)和(12)可得：

其比较结果见表2。其中，相对误差为：

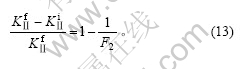
表2  无限板与有限板的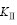相对误差比较

Table 2  Relative error comparison of 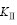between closed-crack in infinite plate and finite plate

从表2可以看出，当a/W≤0.2时，两者相对误差控制在10%以内，可视为无限岩板含裂纹的情况考虑；当a/W＞0.2时，相对误差为20%，此时应视为有限岩板含裂纹的情况考虑。这说明，考虑线弹性断裂力学所确定的无限板的适用范围有一定上限。

2  数值方法

为了与解析分析结果进行比较，对闭合裂尖应力强度因子进行有限元数值计算。设裂纹板的尺寸及材料参数如下：正方形有限板宽度W=150 mm，厚度H=5 mm，裂纹半长a分别取为15，30和45 mm。材料的弹性模量E=30 GPa，泊松比ν=0.3，载荷为均匀分布的压应力σ=10 MPa。裂纹的倾角β分别为15?，30?，45?，60?和75?，侧压系数k分别取0.25和0.5。考虑裂纹面间的摩擦作用，摩擦因数分别取0，0.1，0.2和0.3。

在对模型进行单元划分时，采用三角形退化奇异单元模拟裂纹尖端的应力奇异性。网格生成、节点信息输入与检验均由有限元程序ANSYS完成。为了获得较理想的计算结果，对裂尖邻近区域的单元进行加密处理。同时，裂纹面受力后互相接触，ANSYS提供了接触分析的功能。其解析解和数值解^[12]见表3和表4。

表3  侧压系数为0.25时的裂纹应力强度因子

Table 3  Value of stress intensity factor when side pressure coefficient k=0.25

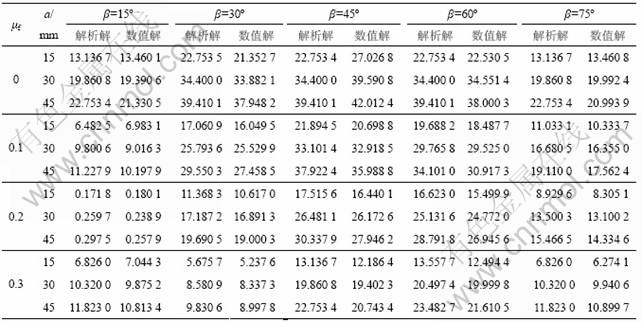
表4  侧压系数为0.5时的裂纹应力强度因子

Table 4  Value of stress intensity factor when the side pressure coefficient k=0.5

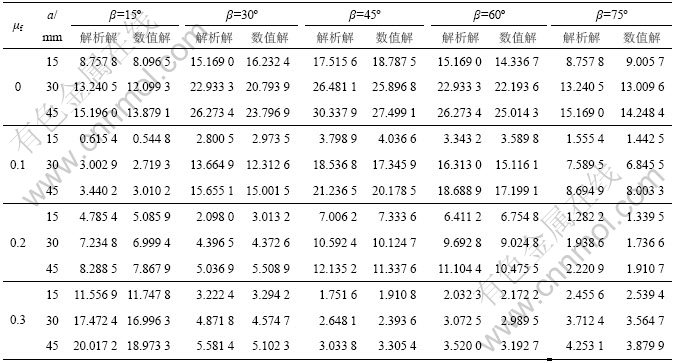
从表3~4可以看出，使用有限单元法计算得出的结果与解析分析所得的结果较吻合，相对误差均在10%以内，能够满足精度要求，从而也验证了本文所推导的有限岩板内含闭合斜裂纹尖端应力强度因子计算公式是正确的。

3  摩擦因数及侧压系数对裂纹应力强度因子的影响

3.1  摩擦因数对裂纹应力强度因子的影响

裂纹受压后闭合，裂纹上下表面间摩擦力的存在影响了裂纹面的相对滑动，从而影响应力强度因子。由式(12)转换得：

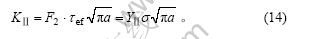
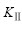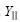从式(14)可知，Ⅱ型裂纹应力强度因子与相关，可由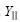-β曲线直观地看出摩擦因数对应力强度因子的影响，见图3和图4。

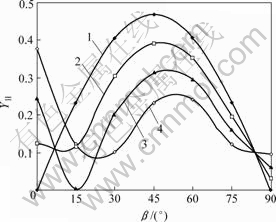
摩擦因素：1—0；2—0.1；3—0.2；4—0.3

图3  侧压系数k=0.25时与β的关系

Fig.3  Relationship between  and  β when side pressure coefficient k=0.25

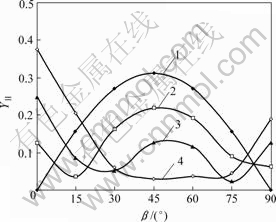
摩擦因素：1—0；2—0.1；3—0.2；4—0.3

图4  侧压系数k=0.5时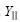与β的关系

Fig.4  Relationship between 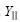 and β when side pressure coefficient k=0.5

从图3和图4可见，有限岩板内含闭合裂纹，当裂纹面间无摩擦影响，即摩擦因数μ_f=0.0时，形状影响因子随着裂纹倾角β的增大而增大，在β=45?时达到最大，以后随之减小。当裂纹面间有摩擦影响时，不同摩擦因数的应力强度因子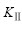的走向大致相似，随着摩擦因数的增大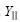，-β曲线逐渐向下移动，这表明裂纹的闭合效应使得裂纹尖端的应力强度因子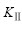降低，从工程安全的角度来说这是有利的。当倾角β在0?~10?之间变化时，应力强度因子的增减与摩擦因数增减一致；当倾角β介于10?~70?时，随着摩擦因数的增大，应力强度因子减小，且每一条曲线的最低点所对应的β也有所减小；当倾角β＞75?时，应力强度因子随摩擦因数的增大而增大。

3.2  侧压系数对裂纹应力强度因子的影响

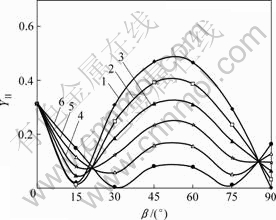
岩体所受到的主压应力随地理环境的不同而千变万化，因此，需要考虑不同侧压系数对裂纹失稳扩展破坏的影响。图5和图6所示为k不同时形状因子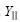与β的关系曲线。

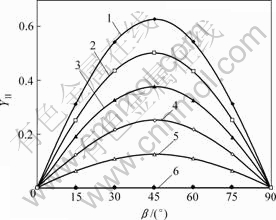
侧压系数：1—0；2—0.2；3—0.4；4—0.6；5—0.8；6—1.0

图 5  摩擦因数μ_f=0, a=30 mm 时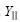与β的关系

Fig.5  Relationship between 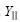 and β when friction coefficient μ_f=0 and a=30 mm

侧压系数：1—0；2—0.1；3—0.2；4—0.3；5—0.4；6—0.5

图 6  摩擦因数μ_f=0.25, a=30 mm 时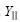与β的关系

Fig.6  Relationship between 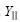 and β when friction coefficient μ_f=0.25 and a=30 mm

可见，当裂纹表面间无摩擦，即μ_f=0时，侧压力为零的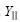-β曲线位于最上方，随着侧压力的增大（即k值增大），相应的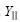-β曲线逐渐向下移动。这表明，侧压力的作用使得裂纹尖端应力强度因子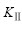降低。当k=1，即双轴等压时，无论β为何值，裂纹尖端应力强度因子均为零。这说明等压条件下的裂纹是不会扩展的，因而不会发生断裂破坏。

当摩擦因数不为零时，侧压系数对应力强度因子的影响还与裂纹的倾角有关。当裂纹倾角很小或很大时，裂纹尖端应力强度因子随着侧压力的增大而增大，但当裂纹倾角在15?~60?范围内时，侧压力的作用会使得裂纹尖端应力强度因子降低。

4  结  论

a. 采用“裂纹线应力场”分析方法，推导出有限岩板闭合裂尖应力强度因子的修正系数为：F₂= 1/[1-(2a/W)²]^1/2。

b. 利用有限元法计算了闭合裂尖的应力强度因子，并与解析方法得出的结果进行了比较，结果表明，采用这2种方法得出的结果基本吻合。

c. 随着裂纹表面摩擦因数的增大，闭合裂尖应力强度因子降低，从工程安全的角度来说，这是有利的。

d. 双轴应力比k增大，可明显降低闭合裂尖的应力强度因子，从而可明显改善闭合裂尖处的应力分布。当双轴应力比k=1即双轴等压时，无论裂纹倾角β为何值，裂尖应力强度因子始终为零，这表明等压条件下裂纹岩板不会发生断裂破坏。

参考文献：

[1] ZHU Zhe-ming, JI Shao-cheng, XIE He-ping. An improved method of collocation for the problem of crack surface subjected to uniform load[J]. Engng Fracture Mech, 1996, 54(5): 731-741.

[2] ZHU Zhe-ming, XIE He-ping, JI Shao-cheng. The mixed boundary problems for a mixed mode crack in a finite plate[J]. Engng Fracture Mech, 1997, 56(5): 647-655.

[3] 谢和平, 朱哲明, 范天佑. 脆性岩石断裂破坏机理的边界配位法分析[J]. 力学学报, 1998, 30(2): 238-246.
XIE He-ping, ZHU Zhe-ming, FAN Tian-you. The analysis of fracture of brittle rock material by using the boundary collocation method[J]. Acta Mechanics Sinica, 1998, 30(2): 238-246.

[4] 夏熙伦, 任 放. 在压缩荷载下岩石和水泥试样的复合型断裂试验及判据[J]. 水利学报, 1984(9): 48-53.
XIA Xi-lun, REN Fang. Cement specimens under compressive loading[J]. Journal of Hydraulic Engineering, 1984(9): 48-53.

[5] 师俊平, 解 敏, 王 静. 无限大平面中斜裂纹的压剪断裂分析[J]. 工程力学, 2006, 23(12): 59-62.
SHI Jun-ping, XIE Min, WANG Jing. Compression and shear fracture analysis of slanting cracks in finite planes[J]. Engineering Mechanics, 2006, 23(12): 59-62.

[6] 王 静, 师俊平. 有限板中裂纹应力强度因子的计算[J]. 岩石力学与工程学报, 2005, 24(6): 963-968.
WANG Jing, SHI Jun-ping. Calculation of stress intensity factor for crack in a finite plate[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 963-968.

[7] SUN Zong-qi. Is crack branching under shear loading caused by shear fracture? A critical review on maximum circumferential stress theory[J]. Trans Nonferrous Met Soc China, 2001, 11(2): 287-292.

[8] 孙宗颀. 如何判断在各种加载下的断裂模式: Ⅰ型还是Ⅱ型[J]. 三峡大学学报: 自然科学版, 2004, 26(1): 27-30.
SUN Zong-qi. How to judge fracture mode under arbitrary loading: ModeⅠ or Mode Ⅱ fracture[J]. J Three Gorges Univ: Natural Sciences, 2004, 26(1): 27-30.

[9] RAO Qiu-hua, SUN Zong-qi1, WANG Gui-yao, et al. Effect of specimen thickness on ModeⅡfracture toughness of rock[J]. J Cent South Univ Technol, 2001, 8(2): 114-119.

[10] CHEN Feng, CAO Ping, RAO Qiu-hua, et al. Use of double edge-eracked Brazilian disk geometry for compression-shear fracture investigation of rock[J]. J Cent South Univ Technol, 2003, 10(3): 211-215.

[11] CHEN Feng, CAO Ping, RAO Qiu-hua, XU Ji-cheng. Mode Ⅱ fracture analysis of double edge cracked circular disk subjected to different diametral compression[J]. J Cent South Univ Technol, 2004, 11(1): 63-68.

[12] 易志坚. 求解应力强度因子的一种方法[J]. 重庆交通学院学报, 1991, 10(3): 37-41.
YI Zhi-jian. One method of calculation stress intensity factor[J]. Journal of Chongqing Jiaotong University, 1991, 10(3): 37-41.

[13] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1993.
China Aviation Academy. Stress intensity factor enchiridion[M]. Beijing: Science Press, 1993.

[14] 孙训方, 方孝淑, 关来泰. 材料力学[M]. 北京: 高等教育出版社, 1994.
SUN Xun-fang, FANG Xiao-shu, GUAN Lai-tai. Material mechanics[M]. Beijing: Higher Education Press, 1994.

[15] 诸武扬. 断裂力学基础[M]. 北京: 科学出版社, 1979.
ZHU Wu-yang. The base of fracture mechanics[M]. Beijing: Science Press, 1979.

[16] 杨 慧. 双轴压缩下含闭合裂纹有限岩板的断裂研究[D]. 长沙: 中南大学资源与安全工程学院, 2007.
YANG Hui. The fracture research of closed-crack in infinite plate under biaxial compression[D]. Changsha: School of Resources and Safety Engineering, Central South University, 2007.

收稿日期：2007-10-25；修回日期：2008-01-28

基金项目：国家自然科学基金资助项目(50774093)；高等学校博士学科点专项科研基金资助项目(20060533071)

通信作者：杨  慧(1981-)，女，湖南益阳人，博士研究生，从事岩石断裂力学研究；电话：13574844830；E-mail: yanghui-dd@163.com