Trans. Nonferrous Met. Soc. China 28(2018) 2520-2527

Phase transition, thermodynamic and elastic properties of ZrC

Jing QIAN¹, Chang-yi WU², Hao-ran GONG¹

1. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;

2. Department of Educational Science, Hunan First Normal University, Changsha 410205, China

Received 17 October 2017; accepted 8 February 2018

Abstract: First principles calculation and quasi-harmonic Debye model were used to obtain more physical properties of zirconium carbide under high temperature and high pressure. The results show that the B1 structure of ZrC is energetically more favorable with lower heat of formation than the B2 structure, and that mechanical instability and positive heat of formation induce the inexistence of the B2 structure at normal pressure. It is also found that the B1 structure would transform to the B2 structure under high pressure below the critical point of V/V₀=0.570. In addition, various thermodynamic and elastic properties of ZrC are obtained within the temperature range of 0-3000 K and the pressure range of 0-100 GPa. The calculated results not only are discussed and understood in terms of electronic structures, but also agree well with corresponding experimental data in the literature.

Key words: ZrC; phase transition; thermodynamic properties; elastic properties; first principles calculation

1 Introduction

During the past years, zirconium carbide (ZrC) has attracted considerable research interests due to its extremely high melting point (3540 °C), superior Vickers hardness (27 GPa), high boiling point (5100 °C), excellent wear and corrosion resistance, high mechanical properties, good thermal and electrical conductivity, and low evaporation, etc [1-12]. The unusual combination of these superior physical and chemical properties of ZrC makes it attractive to be used as cutting tools, wear- resistant coatings, and electrodes, etc [5]. In addition, ZrC has been regarded as hard constituents of metal matrix composites in high-temperature structural applications and nuclear reactors, as well as potential applications in information storage technology, high power industry, and opto-electronic devices [5].

It is well known that the ground state of ZrC at room temperature is a rock-salt cubic structure named  B1 [6,8]. Regarding various properties of the ZrC phase with the B1 structure, the experimental and calculated investigations in the literature are primarily focused on thermal expansion and heat capacity of ZrC, as well as mechanical properties and phase transitions from B1 to B2 (body-centered cubic ordered structure) [1-9,13,14]. Nevertheless, it should be pointed out that the experimental temperature-dependent thermodynamic and mechanical properties of ZrC have been obtained within a limited and dispersive temperature range (e.g., 500-2500 °C [2], 5-350 K [3], 0-300 K [6], 0-1600 K [7]), and that the values of high pressure to induce the B1-B2 phase transition from various theoretical methods were quite different from each other [1-8,13,14].

By means of highly accurate calculations based on density function theory [15,16], the present study is, therefore, dedicated to have a systematic investigation of various properties of ZrC. First principles calculation is used to derive the ground-state properties of ZrC with B1 and B2 structures, as well as the phase transitions from B1 to B2. In addition, first principles calculation is combined with the quasi-harmonic approximation and thermal electronic excitation, to discover the temperature- and pressure-dependent thermodynamic and mechanical properties of ZrC. The derived results are compared extensively with experimental or theoretical evidence in the reference, and the mechanism is discussed in terms of electronic structures, which could deepen the understanding of various properties of ZrC.

2 Theoretical methods

The present first principles calculation is based on the well-established Vienna ab initio simulation package (VASP) within the density functional theory [17]. The calculation is conducted in a plane-wave basis with the projector-augmented wave (PAW) method [18]. The exchange and correlation items are described by generalized gradient approximation (GGA) [19], and the cutoff energy is 450 eV for plane wave basis. For k space integration, the temperature smearing method of METHFESSEL and PAXTON [20] is used for dynamical calculation and the modified tetrahedron method by BLOCHL et al [21] is performed for static calculation.

Accordingly, a unit cell of two atoms (1 Zr and 1 C) is selected for both B1 and B2 structures of ZrC. Gamma centered k grid is adopted for all the calculations: in relaxation calculations for B1 and B2 structures, 11×11×11 and 13×13×13 are used, respectively, while 17×17×17 and 19×19×19 are used in static calculations. The energy criteria are 0.01 and 0.1 meV for electronic and ionic relaxations, respectively, and 0.001 meV for the calculation of DOS and elastic constants.

3 Results and discussion

3.1 Ground-state properties

The ground-state properties of ZrC with B1 and B2 structures at 0 K are calculated by means of first principles calculation. Accordingly, the derived lattice constants (a) of B1 and B2 structures are shown in Table 1. It can be seen that the lattice constant of the B1 structure from this calculation is 4.726 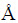, which matches well with the experimental values of 4.68 and 4.698 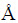in the literature [9]. Moreover, the present lattice constant (2.945 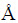) of the B2 structure is also consistent with the corresponding data (2.924 or 3.020 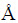) from other calculations [14,23].

Figure 1 displays the calculated total energies of ZrC with B1 and B2 structures as a function of atomic volume. One can observe clearly from this figure that the lowest total energy of the B1 structure corresponding to the equilibrium lattice constant is much smaller than that of the B2 structure. Such a comparison suggests that the B1 structure should be energetically more stable than the B2 structure, which is in good agreement with the observed B1 structure, instead of B2, from experimental studies [1,4]. Interestingly, the two curves of total energies in Fig. 1 have an intersection on the left side of the figure, implying that a phase transition from B1 to B2 would probably happen under high pressure, which will be discussed in Section 3.2.

To investigate the thermodynamic stability of B1 and B2 structures, the heat of formation (ΔH_f) of ZrC is calculated according to the following formula [24]:

ΔH_f=E_ZrC-E_Zr-E_C                              (1)

where E_ZrC, E_Zr and E_C are total energies of ZrC, pure HCP α-Zr, and C (diamond), respectively. Consequently, the derived ΔH_f values are listed in Table 1. It can be seen from Table 1 that the calculated ΔH_f of the B1 structure from the present study is -172.78 kJ/mol, which is compatible with the corresponding value of -185 kJ/mol from experimental observations [24]. Such a large and negative value of ΔH_f indicates the very highly stable nature of the B1 structure. In addition, one can discern from Table 1 that the B2 structure possesses a positive ΔH_f value of 64.79 kJ/mol, which seems much higher than that of B1 structure.

Table 1 Calculated lattice constant (a), heat of formation (ΔH_f), elastic constants (C₁₁, C₁₂, C₄₄), bulk modulus (B), shear modulus (G), elastic modulus (E), and isobaric heat capacities (c_p) of ZrC with B1 and B2 structures

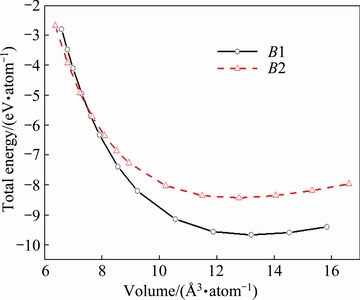
Fig. 1 Total energies of ZrC with B1 and B2 structures

We turn to derive the ground-state mechanical properties of ZrC at 0 K. The elastic constants (C₁₁, C₁₂, and C₄₄) of ZrC are calculated through the strain-energy approach, and the elastic moduli (B, G, and E) are derived by means of the Voigt-Reuss-Hill’s approximation [27]. As a result, the obtained values of C₁₁, C₁₂, C₄₄, B, G, E, and G/B are summarized in Table 1. It can be seen clearly that the calculated elastic constants and elastic moduli of the B1 and B2 structures from the present work are in good agreement with corresponding experimental and calculated data in Refs. [22,25,26].

It is of interest to compare the mechanical stability of the B1 and B2 structures. According to the strain energy theory and born stability criterion [28-30], the strain energy and the matrix of elastic constants of a mechanically stable phase should be positive. By following these guidelines, B1 structure possesses mechanical stability, while the B2 structure is unstable, which is in good agreement with the well-known fact that the B2 structure of ZrC has not been experimentally found so far under normal conditions [1,4]. Considering that the B2 structure has a positive ΔH_f of 64.79 kJ/mol as related before, it is the mechanical instability and positive heat of formation which bring about the inexistence of the B2 structure at normal pressure.

Furthermore, the G/B values of ZrC with B1 and B2 structures are listed in Table 1. It should be pointed out that the G/B ratio has been generally chosen as a primary index to indicate the brittle/ductile behaviors of various materials [31]. One can observe from Table 1 that the calculated G/B value (0.70) of the B1 structure agrees well with the corresponding value from experimental studies [26]. In addition, the derived G/B of the B1 structure seems much bigger than the critical point of 0.57, suggesting that ZrC should be very brittle, which is in excellent agreement with similar experimental observations in the Ref. [26].

3.2 High-pressure phase transition

It is well known that high pressure would alter the atomic arrangement and electronic structures, and therefore has a significant effect on materials behaviors such as mechanical properties, superconductivity, and phase transition. During the past years, the phase transition of ZrC from B1 to B2 under high pressure has been investigated by various theoretical groups [8,13,14, 22,28,32-34]. Nevertheless, the calculated values of critical pressure to trigger the phase transition are quite different from each other, i.e., 289 and 295 GPa from the ultra-soft pseudopotential in the Quantum ESPRESSO and CASTEP codes, respectively [8,13], 313.2 or 303.5 GPa via the FP-LAPW method in WIEN2K [14], 98 or 99 GPa by means of the empirical atomic potentials [28,34], 372 GPa by a three-body force potential model [32], and 525 GPa from plane-wave pseudopotentials implemented in SIESTA [22]. The differences of these critical pressures would be probably attributed to different theoretical methods. In the present work, another theoretical means of PAW-GGA is thus selected to further discover the high-pressure phase transition of ZrC, and it is of interest to compare the current results with those calculated values in the Refs. [8,14,22].

Accordingly, the B1 and B2 structures of ZrC are chosen to discover the phase transition under hydrostatic pressure. The total energies of each structure are calculated as a variation of the scale of the volume (V/V₀) which changes from 2.0 to 0.3 with an interval of 0.04, V and V₀ are actual and the equilibrium volumes of the unit cell. The obtained total energies of B1 and B2 structures are then fitted, respectively, by means of the Vinet’s equation of state (EOS) [27] to derive various values of pressure referring to a series of the scales of the  volume [35].

The energy differences (ΔE) between B1 and B2 structures of ZrC are displayed in Fig. 2 as a function of the scale of volume (V/V₀). One can discern from this figure that the ΔE curve intersects with the line of zero at the value of V/V₀=0.570, and the derived value of critical pressure is 357.624 GPa, which would be considered as the critical point corresponding to the high-pressure phase transition. It should be pointed out that the calculated critical pressure of B1-B2 phase transition from the present PAW-GGA method is constant with the pressure range of 200-550 GPa mentioned above [8,13,14,22,28,32-34].

It is of interest to investigate the effect of pressure on electronic structure of ZrC. Accordingly, Fig. 3 shows the comparison of total densities of states (DOSs) of ZrC with the B2 structure at the V/V₀ values of 1.0 and 0.45. One could observe from Fig. 3 that the electronic structure of the B2 phase at V/V₀=0.45 becomes more delocalized with a larger range of bandwidth and its DOS peaks have much lower height than that at V/V₀=1. In addition, the DOS value at the Fermi level of the B2 phase under high pressure (V/V₀=0.45) is about 0.50 states/(eV·atom), which seems much smaller than the value of 1.35 state/(eV^-1·atom^-1) for the B2 structure at normal condition (V/V₀=1). All the above features of densities of states suggest that high pressure should have an important effect to change the electronic structure and therefore stabilize the B2 structure.

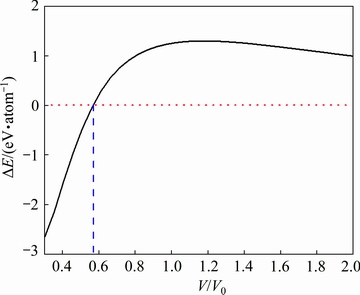
Fig. 2 Energy difference (ΔE) between B1 and B2 structures of ZrC as function of scale of volume (V/V₀)

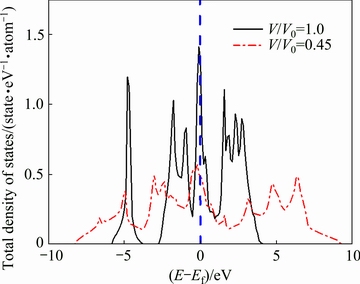
Fig. 3 Total densities of states of ZrC with B2 structure at V/V₀=1.0 and V/V₀=0.45

3.3 Thermodynamic properties

The quasi-harmonic Debye model and thermal electronic excitation are combined in the present study to derive thermodynamic properties of ZrC with the stable B1 structure, as this method has been successfully applied to various thermodynamic calculations [36]. The Helmholtz free energy F(V,T) of ZrC is calculated according the following equation [36]:

F(V,T)=E₀(V)+F_ph(V,T)+F_el(V,T)                 (2)

where E₀(V) is the static total energy at 0 K, and F_ph(V,T) and F_el(V,T) are vibrational and electronic contributions of free energy, respectively.

With the obtained volume-dependent Helmholtz free energy F(V, T), the temperature-dependent volume at ambient pressure, V(T)₀, is fitted by means of the following equation [27]:

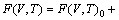
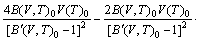
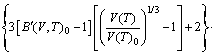
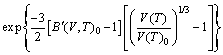      (3)

where B(V,T)₀ and B′(V,T)₀ refer to bulk modulus and pressure derivative of bulk modulus, respectively. The coefficient of thermal expansion (CTE), α(T), is calculated as follows [36]:

                        (4)

The total isochoric heat capacity, c_V, and the isobaric heat capacity, c_p, are then derived [34]. It should be noted that c_V is calculated through the addition of the terms of electronic excitation 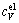 and phonon vibration  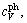which could be obtained by means of the quasi-harmonic Debye model [37]. Accordingly, the calculated 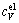, , 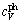c_V and c_p of ZrC with the B1 structure are shown in Fig. 4 as a function of temperature.

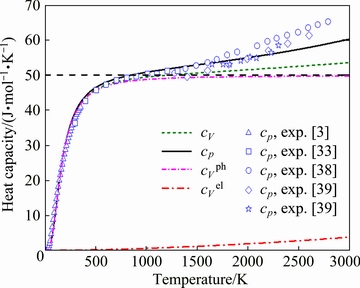
Fig. 4 Temperature-dependent electronic heat capacity 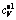, vibrational isochoric heat capacity , total isochoric heat capacity c_V, and isobaric heat capacity c_p of ZrC with B1 structure (The black dash line indicates the Dulong and Petit limit at high temperature)

It can be observed clearly from Fig. 4 that the present heat capacities of the B1 structure of ZrC agree well with experimental observations in Refs. [3,33,38,39]. For instance, the derived c_p value of B1 ZrC at 300 K is 39.72 J/(mol^-1·K^-1), which is in good agreement with the corresponding experimental value of 38.04 J/(mol^-1·K^-1) [3]. These nice agreements indicate that the present theoretical model would be relevant to reveal thermodynamic properties of ZrC. Interestingly, one could also discern that the curves of 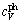, c_V, and c_p exhibit a considerable increase below the temperature of 450 K, and that the c_p value at a certain temperature is generally larger than that of c_V. It can be also seen clearly from Fig. 4 that the  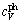value approaches the Dulong and Petit limit (about 50 J/(mol^-1·K^-1) at high temperature, which is consistent with similar observations in Ref. [40].

Furthermore, Fig. 5 displays the coefficients of thermal expansion (CTE, α) as a function of temperature. It can be clearly seen from Fig. 5 that the calculated values from the present work are consistent with corresponding data from experimental observations by other groups [33]. One could also discern from Fig. 5 that CTE of the B1 structure increases dramatically as a function of temperature below 500 K, and a nearly linear and gradual rise of CTE is followed with the increase of temperature. In addition, at a certain temperature, CTE decreases with the increase of pressure.

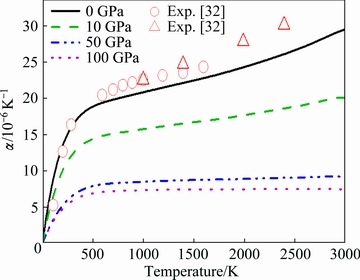
Fig. 5 Coefficients of thermal expansion (α) with B1 structure as function of temperature

3.4 Mechanical properties

The temperature dependent elastic constants of ZrC with the B1 structure are obtained by means of the method in Ref. [36], and the principal procedure is described as follows. Firstly, the volume dependent elastic constants C_ij(V) are derived, according to the universal-linear-independent coupling-strain (ULICS) method [41], at a volume range from V/V₀ of 0.75 to 1.25 with an interval of 0.025. Secondly, the bulk modulus, B(V), is calculated as a function of volume by means of Eq. (3) in Section 3.3.

Thirdly, the bulk modulus, B(T), and elastic constants, C_ij(T), are obtained as a function of temperature through replacing V(T)₀ in the forms of B(V) and C_ij(V). It should be pointed out that the values of V(T)₀ have been calculated by means of Eq. (3) in Section 3.3. Fourthly, the obtained elastic constants are then applied to deriving the temperature-dependent shear modulus (G) and elastic modulus (E) of polycrystalline ZrC through the Voigt-Reuss-Hill’s approximations.

Consequently, the obtained elastic constants of ZrC with the B1 structure are displayed in Fig. 6(a) as a function of temperature. It can be observed from this figure that the calculated C₄₄ values from this work match well with the corresponding values from experiments [6], while the present values of C₁₁ and C₁₂ seem a little smaller than the corresponding experimental data within the low temperature range [6]. One can also notice obviously from Fig. 6(a) that the elastic constants at a certain temperature have an ascending sequence of C₁₂→C₄₄→C₁₁ within the entire temperature range, and that each elastic constant descends almost linearly as a function of the temperature.

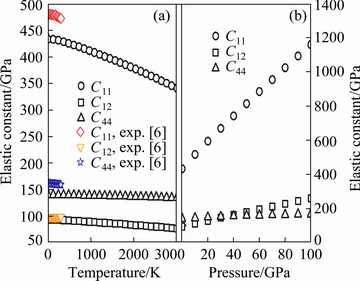
Fig. 6 Temperature-dependent (a) and pressure-dependent (b) elastic constant of ZrC with B1 structure ((a) and (b) are at normal pressure and 0 K, respectively)

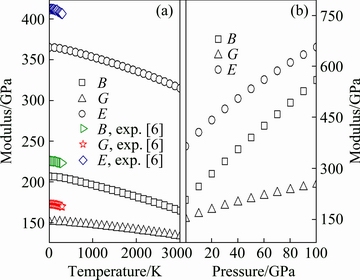
Fig. 7 Temperature-dependent (a) and pressure-dependent (b) bulk modulus (B), shear modulus (G), and elastic modulus (E) of polycrystalline ZrC with B1 structure ((a) and (b) are at normal pressure and 0 K, respectively)

Moreover, the temperature-dependent moduli of the B1 structure of ZrC are summarized in Fig. 7(a). It can be deduced clearly that each curve of B, G, and E exhibits a nearly linear decrease with the increase of temperature. One could also find out that the calculated values of B, G, and E are consistent with experimental evidence in Ref. [6]. Interestingly, one could see from Fig. 6(b) and Fig. 7(b) that all the elastic constants and elastic moduli increase almost linearly with the increase of pressure.

It is of importance to understand the temperature- and pressure-dependent mechanical properties in terms of electronic structures [42,43]. As a typical example, Fig. 8 shows the comparison of charge density plots of the B1 structure of ZrC at three volumes of the unit cell, V/V₀ =1.0, 1.1, and 0.9. It can be discerned clearly from Fig. 8 that the charge densities between Zr and C atoms at the equilibrium volume (V/V₀=1.0) are lower and higher than the corresponding values when ZrC is under compression (V/V₀=0.9) and expansion (V/V₀=1.1), respectively, indicating that the chemical bonding of ZrC would become weaker and stronger as a result of the increase of temperature and pressure, and vice versa. The above changes of charge densities due to volume variation would therefore bring about a fair understanding to the increase of mechanical properties of ZrC with the decrease of temperature or the increase of pressure as displayed in Figs. 6 and 7.

4 Conclusions

1) Ab initio calculation was used to derive the ground-state properties and phase transition of ZrC with B1 and B2 structures. In addition, the quasi-harmonic Debye model and thermal electronic excitation were combined with ab initio calculation to obtain various thermodynamic and mechanical properties of ZrC as a function of temperature and pressure.

2) It is revealed that B1 structures are thermodynamically stable with large and negative ΔH_f values, while the B2 structure could not be fabricated under normal conditions due to its positive ΔH_f and mechanical unstableness.

3) Calculation also shows that the B1→B2 phase transition could be triggered below the critical volume of V/V₀=0.570 with the high pressure of 357.624 GPa, and that the large differences of critical pressure in the literature would be attributed to different theoretical methods.

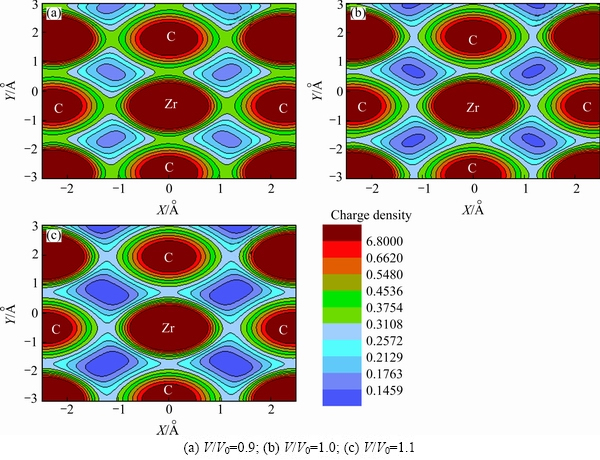
Fig. 8 Charge density plots of B1 structure of ZrC at different conditions

4) Moreover, the c_p and CTE values of ZrC increase with the increase of temperature, CTE values decrease with the increase of pressure. The elastic constants (C₁₁, C₁₂, and C₄₄) and elastic moduli (B, G, and E) of ZrC increase with the increase of pressure and decrease with the increase of temperature.

References

[1] HOUSKA C R. Thermal expansion and atomic vibration amplitudes for TiC, TiN, ZrC, ZrN, and pure tungsten [J]. Journal of Physics and Chemistry of Solids, 1964, 25: 359-366.

[2] RICHARDSON J H. Thermal expansion of three group IVA carbides to 2700 C [J]. Journal of the American Ceramic Society, 1965, 48: 497-499.

[3] WESTRUM E F Jr, FEICK G. Zirconium carbide: Heat capacity and thermodynamic properties from 5 to 350 °C [J]. Journal of Chemical and Engineering Data, 1963, 8: 176-178.

[4] ELLIOTT R O, KEMPTER C P. Thermal expansion of some transition metal carbides [J]. The Journal of Physical Chemistry, 1958, 62: 630-631.

[5] VARSHNEY D, SHRIYA S. Elastic, mechanical and thermodynamic properties at high pressures and temperatures of transition metal monocarbides [J]. International Journal of Refractory Metals and Hard Materials, 2013, 41: 375-401.

[6] CHANG R, GRAHAM L J. Low-temperature elastic properties of ZrC and TiC [J]. Journal of Applied Physics, 1966, 37: 3778-3783.

[7] HANNINK R H J, MURRAY M J. Elastic moduli measurements of some cubic transition metal carbides and alloyed carbides [J]. Journal of Materials Science, 1974, 9: 223-228.

[8] IVASHCHENKO V I, TURCHI P E A, SHEVCHENKO V I. Phase transformation B1 to B2 in TiC, TiN, ZrC and ZrN under pressure [J]. Condensed Matter Physics, 2013, 16: 33602-1-9.

[9] FU Hong-zhi, PENG Wei-min, GAO Tao. Structural and elastic properties of ZrC under high pressure [J]. Materials Chemistry and Physics, 2009, 115: 789-794.

[10] LI Jun, YANG Xin, SU Zhe-an, XUE Liang, ZHONG Ping, LI Shuai-peng, HUANG Qi-zhong. Effect of ZrC-SiC content on microstructure and ablation properties of C/C composites [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 2653-2664.

[11] LIU Chun-xuan, CHEN Jia-xun, SU Zhe-an, YANG Xin, CAO Liu-xu, HUANG Qing-zhong. Pyrolysis mechanism of ZrC precursor and fabrication of C/C-ZrC composites by precursor infiltration and pyrolysis [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 1779-1784.

[12] ZHANG Zhong-wei, ZHEN Qiang, ZHENG Feng, LU Fei, NAN Ce-wen, LI Rong, WANG Jun-shan. High-temperature diffusion behavior of ZrC in C matrix and its promotion on graphitization [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 2257-2262.

[13] HAO Ai-min, ZHOU Tie-jun, ZHU Yan, ZHANG Xin-yu, LIU Ri-ping. First-principles investigations on electronic, elastic and thermodynamic properties of ZrC and ZrN under high pressure [J]. Materials Chemistry and Physics, 2011, 129: 99-104.

[14] LV Zeng-tao, HU Hai-quan, WU Cheng, CUI Shou-xin, ZHANG Gui-qing, FENG Wen-xian. First-principles study of structural stability, electronic and elastic properties of ZrC compounds [J]. Physica B: Condensed Matter, 2011, 406: 2750-2754.

[15] LIU Liu-cheng, WANG Ji-wei, QIAN Jing, HE Yue-hui, GONG Hao-ran, LIANG Chao-ping, ZHOU Sheng-feng. Fundamental effects of Ag alloying on hydrogen behaviors in PdCu [J]. Journal of Membrane Science, 2018, 550: 230-237.

[16] YANG Jia-xi, ZHAO Heng-lv, GONG Hao-ran, SONG Min, REN Qing-qiang. Proposed mechanism of HCP→FCC phase transition in titanium through first principles calculation and experiments [J]. Scientific Reports, 2018, 8: 1992-1-9.

[17] KRESSE G, HAFNER J. Ab initio molecular dynamics for open-shell transition metals [J]. Physical Review B, 1993, 48: 13115.

[18] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59: 1758-1775.

[19] PERDEW J P, CHEVARY J A, VOSKO S H, JACKSON K A, PEDERSON M R, SINGH D J, FIOLHAIS C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1992, 46: 6671-6687.

[20] METHFESSEL M, PAXTON A T. High-precision sampling for Brillouin-zone integration in metals [J]. Physical Review B, 1989, 40: 3616-3621.

[21] BLOCHL P E, JEPSEN O, ANDERSEN O K. Improved tetrahedron method for Brillouin-zone integrations [J]. Physical Review B, 1994, 49: 16223-16233.

[22] MECABIH S, AMRANE N, NABI Z, ABBAR B, AOURAG H. Description of structural and electronic properties of TiC and ZrC by generalized gradient approximation [J]. Physica A: Statistical Mechanics and its Applications, 2000, 285: 392-396.

[23] CHAUHAN M, GUPTA D C. Electronic, mechanical, phase transition and thermo-physical properties of TiC, ZrC and HfC: High pressure computational study [J]. Diamond and Related Materials, 2013, 40: 96-106.

[24] LIU Yang-zen, JIANG Ye-hua, ZHOU Rong, FENG Jing. First principles study the stability and mechanical properties of MC (M= Ti, V, Zr, Nb, Hf and Ta) compounds [J]. Journal of Alloys and Compounds, 2014, 582: 500-504.

[25] WEBER W. Lattice dynamics of transition-metal carbides [J]. Physical Review B, 1973, 8: 5082-5092.

[26] BROWN H L, KEMPTER C P. Elastic properties of zirconium carbide [J]. Physica Status Solidi (b), 1966, 18(1): 18-20.

[27] MA Guo-cheng, FAN Jing-lian, GONG Hao-ran. Mechanical behavior of Cu-W interface systems upon tensile loading from molecular dynamics simulations [J]. Computational Materials Science, 2018, 152: 165-168.

[28] BHARDWAJ P, SINGH S. Structural phase stability and elastic properties of refractory carbides [J]. International Journal of Refractory Metals and Hard Materials, 2012, 35: 115-121.

[29] MILSTEIN F, HILL R. Divergences among the born and classical stability criteria for cubic crystals under hydrostatic loading [J]. Physical Review Letters, 1979, 43: 1411-1413.

[30] QIAN Jing, WU Chang-yi, FAN Jing-lian, GONG Hao-ran. Effect of alloying elements on stacking fault energy and ductility of tungsten [J]. Journal of Alloys and Compounds, 2018, 737: 372-376.

[31] PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals [J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1954, 45: 823-843.

[32] DIWAN B D. Structural phase transition of refractory metal carbides at high pressure [J]. Canadian Journal of Physics, 2013, 92: 415-419.

[33] ABDOLLAHI A. First-principle calculations of thermodynamic properties of ZrC and ZrN at high pressures and high temperatures [J]. Physica B: Condensed Matter, 2013, 410: 57-62.

[34] SINGH A, AYNYAS M, SANYAL S. Phase transition and high pressure behavior of zirconium and niobium carbides [J]. Open Physics, 2009, 7: 102-107.

[35] YANG Jia-xi, LIU Liu-cheng, GONG Hao-ran, SONG Min. Proposed mechanism of twin formation during hexagonal-close- packed structure to face-centered-cubic phase transition [J]. Solid State Communications, 2018,284-286:40-44.

[36] LIANG Chao-ping, WU Chang-yi, FAN Jing-lian, GONG Hao-ran, Structural, thermodynamic, and mechanical properties of WCu solid solutions [J]. Journal of Physics and Chemistry of Solids, 2017, 110: 401-408.

[37] WU Chang-yi, HAN Jin-cheng, SUN Lei, GONG Hao-ran, LIANG Chao-ping. Effects of trigonal deformation on electronic structure and thermoelectric properties of bismuth [J]. Journal of Physics: Condensed Matter, 2018,30:285504-1-13.

[38] LEVINSON L S. High-temperature heat contents of TiC and ZrC [J]. The Journal of Chemical Physics, 1965, 42: 2891-2892.

[39] DUFF A I, DAVEY T, KORBMACHER D, GLENSK A, GRABOWSKI B, NEUGEBAUER J, FINNIS M W. Improved method of calculating ab initio high-temperature thermodynamic properties with application to ZrC [J]. Physical Review B, 2015, 91: 214311.

[40] KRASNENKO V, BRIK M G. First-principles calculations of hydrostatic pressure effects on the structural, elastic and thermodynamic properties of cubic monocarbides XC (X= Ti, V, Cr, Nb, Mo, Hf) [J]. Solid State Sciences, 2012, 14: 1431-1444.

[41] YU Rong, ZHU J, YE H Q. Calculations of single-crystal elastic constants made simple [J]. Computer Physics Communications, 2010, 181: 671-675.

[42] QIAN Jing, WU Chang-yi, GONG Hao-ran, ZHOU Sheng-feng. Cohesion properties of W-ZrC interfaces from first principles calculation [J]. Journal of Alloys and Compounds, 2018, 768: 387-391.

[43] CHEN Liang, WANG Qian, XIONG Lei, GONG Hao-ran. Computationally predicted fundamental behaviors of embedded hydrogen at TiC/W interfaces [J]. International Journal of Hydrogen Energy, 2018, 43: 16180-16186.

ZrC的相变以及热力学和弹性性质

钱 静¹，吴昌义²，龚浩然¹

1. 中南大学 粉末冶金国家重点实验室，长沙 410083；

2. 湖南第一师范学院 教育科学学院，长沙 410205

摘  要：采用第一性原理计算，结合准谐近似德拜模型深入研究高温高压下ZrC的性能。结果表明，ZrC的B1结构比B2结构具有更低的生成热，说明B1结构的ZrC更稳定，此外，力学不稳定性和正的生成热是B2结构的ZrC在常压下不存在的原因。研究还发现，B1结构的ZrC在V/V₀=0.570的临界点以下可以转化为B2结构。另外，通过第一性原理计算和准谐近似德拜模型，分别在0~3000 K的温度范围内和0~100 GPa的压力范围内研究ZrC的各种热力学和弹性性质。对ZrC电子结构的各种性质进行讨论和说明，计算结果与文献中相应的实验数据吻合较好。

关键词：ZrC；相变；热力学性质；弹性性质；第一性原理计算

(Edited by Xiang-qun LI)

Foundation item: Project (2014GB115000) supported by Key Project of ITER of Ministry of Science and Technology of China; Project supported by State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China

Corresponding author: Hao-ran GONG; Fax: +86-731-88710855; E-mail: gonghr@csu.edu.cn

DOI: 10.1016/S1003-6326(18)64898-8