大直径气力反循环钻头结构参数数值模拟与优化
赵志强,殷琨,博坤,殷其雷,张五钊
(吉林大学 建设工程学院,吉林 长春,130021)
摘要:为实现大直径嵌岩桩孔在浅孔和干孔时的气力反循环排渣,解决无法使用气举和泵吸反循环排渣的技术难题,设计基于引射器原理的大直径潜孔锤气力反循环钻头。采用正交试验设计方法,运用计算流体动力学(CFD)仿真技术,探索引射器原理在大直径钻井反循环排渣中应用的可行性。理论分析表明:钻头结构的6个关键参数即喷嘴直径(Dn)、喷嘴数量(N)、喷嘴长度(L)、喷嘴倾斜角度(θs)、喷嘴偏转角度(θd)和引导段直径(Dg)直接影响着排渣效果;基于引射器原理设计的大直径钻头反循环效果可靠、稳定;当GQF-16潜孔锤供风量为50 m3/min,钻头直径为1.2 m时,Dn=20 mm,N=3,L=50 mm,θs=35°,θd=10°,Dg=50 mm为钻头最优理论结构参数组合。
关键词:大直径钻头;气力反循环;引射器;计算流体动力学;正交设计
中图分类号:TE247 文献标志码:A 文章编号:1672-7207(2013)10-4264-09
Numerical simulation and optimization of structural parameters on large-diameter air reverse circulation DTH hammer bit
ZHAO Zhiqiang, YIN Kun, BO Kun, YIN Qilei, ZHANG Wuzhao
(College of Construction Engineering, Jilin University, Changchun 130021, China)
Abstract: In order to achieve cutting transport with air reverse circulation in dry and shallow large-diameter holes of rock-socketed pile, and solve the technical problem with air-lift and pump reverse circulation, a large-diameter reverse circulation bit was innovatively designed based on ejecting theory. Meanwhile, the orthogonal design method and computational fluid dynamics (CFD) simulation technique were applied to explore the application feasibility of ejector theory in use of in air reverse circulation drilling. Through theory analysis, six key geometry parameters of air reverse circulation bit were proved to have direct effect on the function of cutting transport, including the diameter of nozzles (Dn), the number of nozzles (N), the length of nozzles (L), the angle of inclination (θs), the angle of deflection (θd) and the diameter in induced segment(Dg). Each parameter was analysed and optimized to reveal influence law of structural parameters on reverse circulation cutting transport. The results show that the reverse circulation effect of large diameter bit designed based on ejecting theory is absolutely valid and stable. Furthermore, while the supplied air volume of GQF-16 DTH hammer reaches to 50 m3/min and diameter of the bit goes to 1.2 m, a configuration of parameters with Dn=20 mm, N=3, L=50 mm, θs=35°, θd=10°, Dg=50 mm are the most ideal parameter combinations.
Key words: large-diameter DTH hammer bit; air reverse circulation; ejector; computational fluid dynamics; orthogonal design
大直径嵌岩桩(桩径d≥0.8m)因具有单桩承载力大、抗震能力强、桩顶沉降量小等优点,被广泛应用于高层及超高层建筑、港口码头、水库坝基、公路及铁路桥梁、围海造田地基加固和煤矿抽排瓦斯通风井、投料井等工程[1-3]。大直径嵌岩桩施工中可采用大直径潜孔锤钻进或旋挖钻机大直径潜孔锤联合施工工艺方法[4],后者可发挥2种施工工艺的优点,加快嵌岩桩孔施工速度和质量。但大直径潜孔锤施工过程中,由于钻杆与孔壁之间外环空断面积较大,采用正循环不能满足排渣要求[5],而反循环排渣因上返通道断面积较小,不受桩孔直径变化的影响[6],常用于嵌岩桩施工。但是在浅孔孔段、干孔或缺水、破碎漏失等地层时,常用的泵吸、气举反循环均无法使用[7]。为实现大直径嵌岩桩孔施工中气力反循环排渣,突破无法使用常规气举和泵吸反循环的技术瓶颈,解决浅孔和干孔段排渣难题,避免孔底岩屑重复破碎对钻头球齿的磨损[8],将广泛应用的流体引射器原理引入到钻头的反循环排渣结构,设计气力反循环钻头。在钻头结构参数设计过程中,采用正交试验设计方法,运用计算流体动力学(CFD)仿真技术,探讨引射器原理应用于气力反循环结构的可行性,同时总结分析各结构参数对反循环排渣效果的影响,以及为气力反循环钻头结构参数设计提供依据。
1 引射器原理与气力反循环
引射器利用高速射流的紊动扩散作用,使2股不同压力的流体相互混合并产生能量交换,已被广泛地应用于化工、军事等领域[9]。引射器结构包括:喷嘴、接收室、混合室和扩压室,其工作原理如图1所示:高压气流从喷嘴1高速喷出,被引射气流在引射气流的剪切作用下,被卷吸进入混合室3,继续与引射气流发生动量、能量交换,逐渐在扩压室4形成单一均匀的混合气流[10-12]。
GQF-16大直径潜孔锤气力反循环钻具系统原理如图2所示:由空压机1输出的压缩空气经进气管2、气水龙头3、主动钻杆5、双壁钻杆6、进入潜孔锤7,驱动活塞冲击做功,驱动活塞做功后的压缩空气借助钻头内部的引射器结构引导流体进入双壁钻杆中心通道,形成孔底负压区,抽吸钻头8与孔壁之间外环空的空气,并携带钻头破碎的岩屑快速上返至地表。
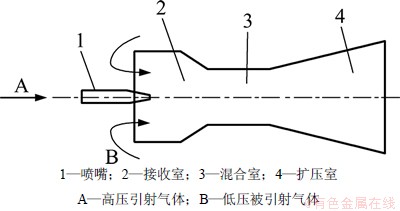
图1 单级气体引射器原理图
Fig. 1 Schematic diagram of single gas ejector
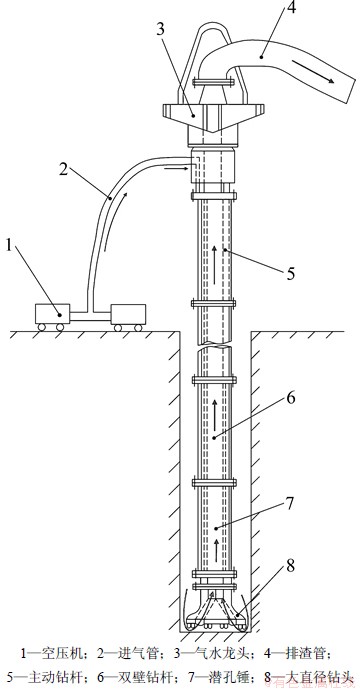
图2 GQF-16大直径潜孔锤气力反循环钻具系统图
Fig. 2 Diagram of GQF-16 large diameter DTH air reverse circulation drilling tool
基于引射器原理设计的大直径气力反循环钻头的工作原理(见图3)是:压缩空气在驱动活塞2作功后,经由花键套7与花键轴8之间的间隙,进入花键轴8内部的导引孔,再经由喷嘴高速喷出;喷出的高速气流卷吸周围流体,在孔底形成负压区,进而抽吸钻头9与孔壁之间的外环空的空气,2股气流混合后携带钻头破碎的岩屑,经由芯管1高速上返至地表。
根据大直径潜孔锤结构特点,气力反循环钻头的主要结构参数有6个(见图4):(1) 喷嘴直径Dn;(2) 喷嘴数量N;(3)喷嘴长度L;(4) 喷嘴倾斜角度θs;(5) 喷嘴偏转角度θd;(6) 引导段直径Dg。
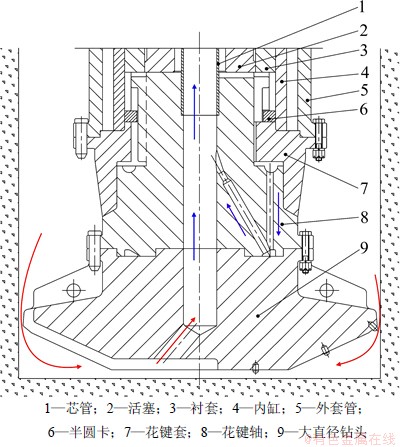
图3 气力反循环钻头结构原理图
Fig. 3 Schematic diagram of structure of air reverse circulation bit
2 CFD建模
2.1 数学模型
流体流动要受物理守恒定律的支配,基本的守恒定律包括:质量守恒定律、动量守恒定律和能量守恒定律[13]。
质量守恒方程为
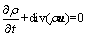 (1)
(1)
动量守恒方程为
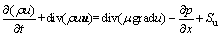 (2)
(2)
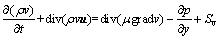 (3)
(3)
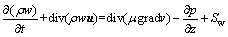 (4)
(4)
能量守恒方程为
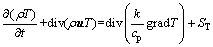 (5)
(5)
其中:div为散度;u为速度矢量;u,v和w分别为速度矢量 u在x,y和z方向的分量;ρ为液体密度;μ为动力黏度;p为压强;k为流体传热系数;cp为比热容;Su,Sv和Sw为动量守恒方程的广义源项[14]。
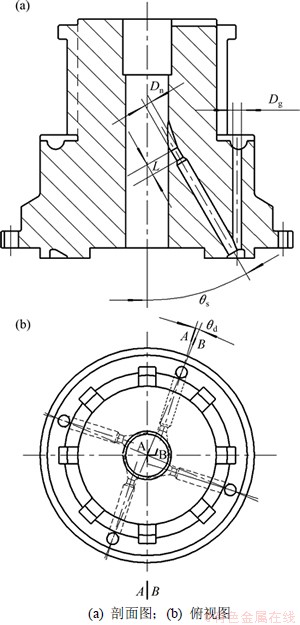
图4 气力反循环钻头结构参数图
Fig. 4 Schematic diagram of structural parameters of air reverse circulation bit
2.2 CFD建模
采用三维CAD软件Solidworks建立钻头内部流体流动区域模型,在满足计算精度的前提下,结合所配置计算机的计算能力,用前处理软件Hypermesh划分网格,见图5。CFD模型网格数量控制在(30~40)万个,其中六面体网格所占比例为78%~92%。
在Fluent求解过程中,为提高求解的精度和收敛的速度,采用SIMPLEC算法对对流项采用二阶迎风格式进行离散;近壁面采用标准壁面函数法[15]。在Fluent分析过程中,设置质量入口边界条件和压力出口边界条件;同时设置残差监视(动量方程、湍动耗散率、湍动能残差均为10-7,连续性方程残差为10-5,能量方程残差为10-6)和出入口质量流量监视,以这2个监视值作为收敛与否的判定标准[16]。
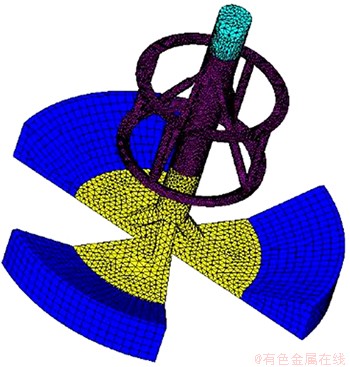
图5 CFD网格模型
Fig. 5 CFD grid model
3 正交试验设计
气力反循环钻头结构参数优化设计中,如每个结构参数选3个变量,那么,这6个参数全面数值模拟的模型数量是36(即729)个,CFD计算会十分繁重,并且统计分析数据及总结各参数变化规律也很繁琐。
若采用正交试验设计来科学地安排CFD数值模拟,则CFD模型数量会大大减少,而且数据统计也会简化[17-19]。
首先,选用L8(27)正交表,对6个钻头结构参数各选2个水平,确定各参数之间的主次顺序,同时检查任意2个参数之间是否存在交互作用。经过对6个参数15种组合的计算分析,各因素之间均不存在交互作用。
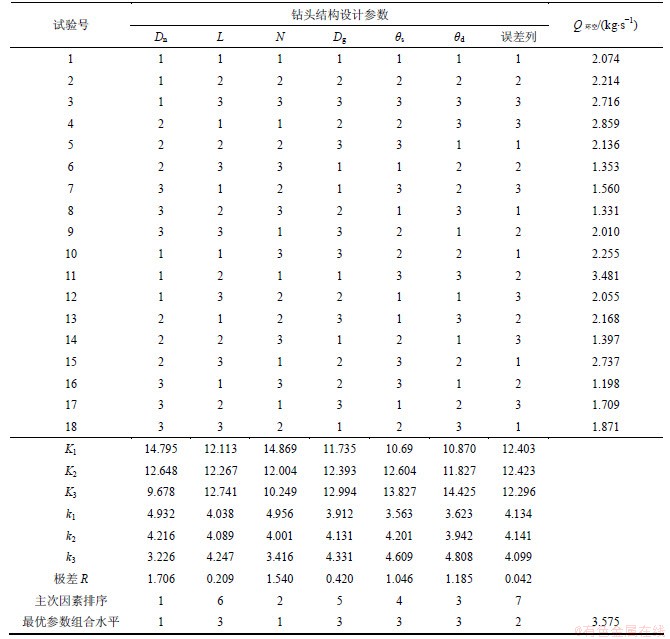
最后,采用L18(37)正交表,对6个钻头结构参数进行3水平正交试验设计,见表1。引入“外环空空气抽吸质量(Q环空)”概念,作为试验评价指标:Q环空>0, 说明外环空空气被吸入中心通道,Q环空反映引射器的抽吸能力,其值越大说明抽吸能力越强,反循环的效果也越好;Q环空=0, 说明压缩气体通过引射器后既不抽吸外环空空气,也没进入外环空;Q环空<0, 说明钻头不能吸入外环空空气,反循环失效,在设计中,需要避免这种情形。
4 CFD计算结果分析
在进风量不变的前提下,对L18(37)交表中得到的Q环空数值进行回归分析,总结参数变化对反循环排渣效果的影响规律。
4.1 喷嘴长度L、引导段直径Dg变化时,喷嘴直径Dn变化对Q环空的影响规律
图6所示为喷嘴长度L、引导段直径Dg变化时,Q环空随Dn的变化规律。从图6可见:当Dg和Dn不变,L变化时,目标值Q环空的变化幅度不大。当L和Dg不变,Dn由15 mm增至40 mm时,Q环空先增大后减小。无论L和Dg如何组合,Q环空的最大值均出现在Dn=20 mm附近。
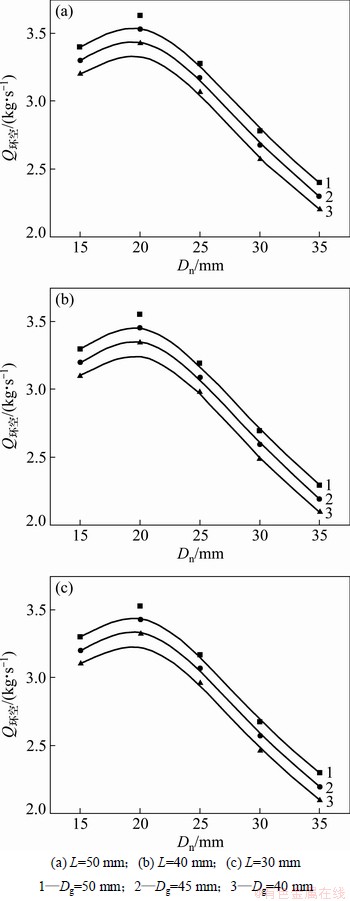
图6 Dg变化时,Q环空随Dn的变化规律
Fig. 6 Effect of Dn on Q环空 at different Dg
表1 钻头结构设计参数 L18(37) 正交表
Table 1 L18(37) orthogonal table for structural parameter of DTH hammer bit
因为压缩气体通过喷嘴高速喷出,对低速流体产生卷吸作用,形成“文丘里效应”,在钻头底部产生负压区,从而抽吸外环空的空气进入芯管。当Dn过小时,喷嘴局部压力损失会增大,活塞底部的背压也会增大,压缩气体的能量不能有效地转化为活塞的冲击能,会造成能量浪费;当Dn过大时,压缩气体的流速会降低,引射流体对外环空空气的抽吸作用会减弱。因此,在钻头设计过程中,为达到最优的反循环效果,Dn应尽量选在20 mm附近。
4.2 引导段直径Dg、喷嘴直径Dn变化时,喷嘴数量N变化对Q环空的影响
图7所示为引导段直径Dg、喷嘴直径Dn变化时,Q环空随N的变化规律。从图7可见:当N和Dn一定时,Dg变化,Q环空变化的幅度很小;Dg和Dn不变时,喷嘴数量N由2个增至6个,Q环空先增大后减小。不管Dg和Dn怎么变化,均是N=3时,Q环空出现最大值。
因为Dn一定,N增加,喷嘴总断面积增加,压缩空气经过喷嘴后流速降低,从而减弱引射流体的卷吸能力,并且喷出的流体之间会形成干扰,不利于引射流体在孔底形成负压区。当N过小时,流经喷嘴的局部压力损失会增加,造成压缩气体能量损失,也会降低引射气体对外环空空气的抽吸能力。
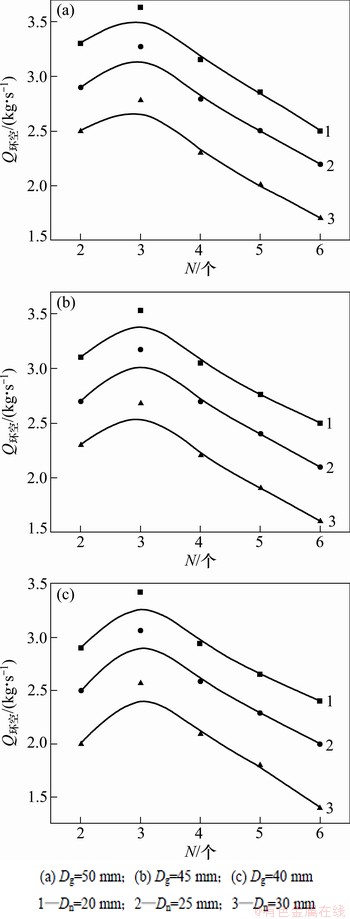
图7 Dn变化时,Q环空随N的变化规律
Fig. 7 Effect of N on Q环空at different Dn
因此,为使气力反循环钻头的反循环效果达到最优,喷嘴数量N应选3个。
4.3 喷嘴直径Dn、引导段直径Dg变化时,喷嘴长度L变化对Q环空的影响规律
图8所示为喷嘴直径Dn、引导段直径Dg变化时,Q环空随L的变化规律。从图8可见:当L和Dg一定,Dn变化时,Q环空波动幅度较大;当Dn和Dg一定时,随着L由30 mm增加到70 mm,Q环空先缓慢增大;在L=50 mm附近时,Q环空取得最大值,然后Q环空减小。不管Dn和Dg怎么组合,Q环空的最大值均出现在L=50 mm附近。
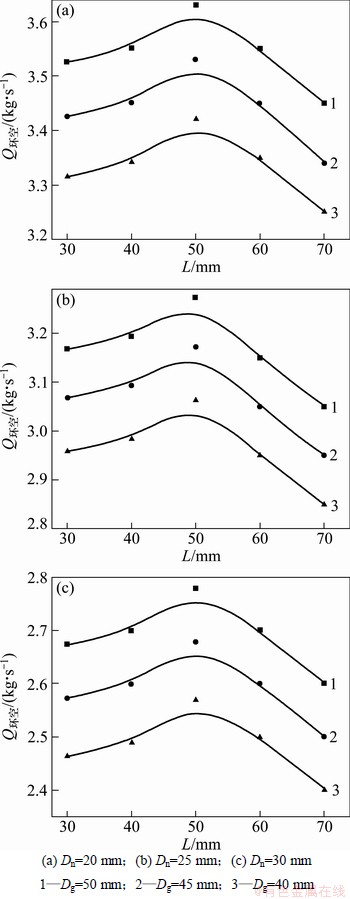
图8 Dg变化时,Q环空随L的变化规律
Fig. 8 Effect of L on Q环空 at different Dg
这是因为喷嘴长度L过短时,经由喷嘴喷射出的流体会发散,减弱了引射流体的引射能力,但是,当L过长时,虽然喷射出的流体成束性好,但喷嘴处的局部压力损失又过大,同样降低了引射流体的引射能力。因此,在钻头结构参数设计中,喷嘴长度L选值应靠近50 mm。
4.4 喷嘴直径Dn、喷嘴偏转角度θd变化时,喷嘴倾斜角度θs对Q环空的影响规律
图9所示为喷嘴直径Dn、喷嘴偏转角度θd变化时,Q环空随θs的变化规律。从图9可见:当Dn和θs一定,Dn变化时,Q环空的数值波动较大;当Dn和θd一定时,随着θs由20°增加到40°,Q环空先增大再减小。并且无论Dn和θd参数如何组合,θs=35°附近时,Q环空均出现最大值。
因为喷嘴倾斜角度过小时,流体流动的距离长,沿程损失增大,从而降低高速流体的卷吸能力。当倾斜角度过大时,高速喷射流体会直接撞击芯管内壁,产生射流漫反射现象,同时产生紊流,不利于引射流体抽吸外环空的气体进入中心通道。
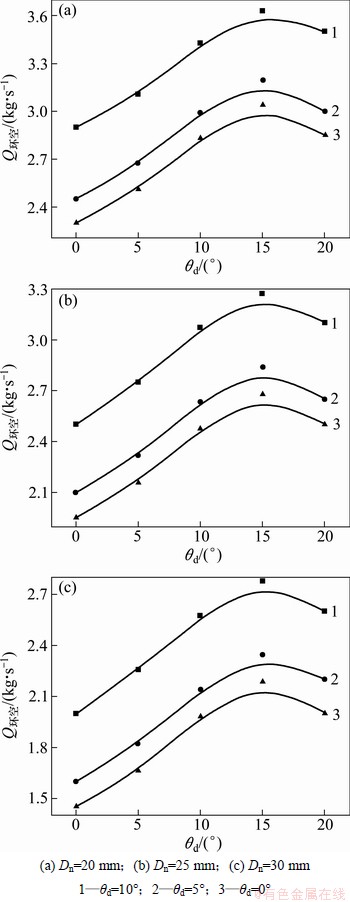
图9 θd变化时,Q环空随θs的变化规律
Fig. 9 Effect of θs on Q环空 at different θd
所以,在钻头设计过程中,喷嘴的倾斜角度应尽量靠近35°。
4.5 喷嘴直径Dn、喷嘴倾斜角度θs变化时,喷嘴偏转角度θd对Q环空的影响规律
图10所示为喷嘴直径Dn、喷嘴倾斜角度θs变化时,Q环空随θd的变化规律。从图10中可见:θs和θd一定,随着Dn的变化,Q环空变化波动较大;Dn和θs一定时,随着θd由0°增大到20°,Q环空先增大后减小。无论Dn和θs怎么组合,当θd在10°附近时,Q环空均取得最大值。
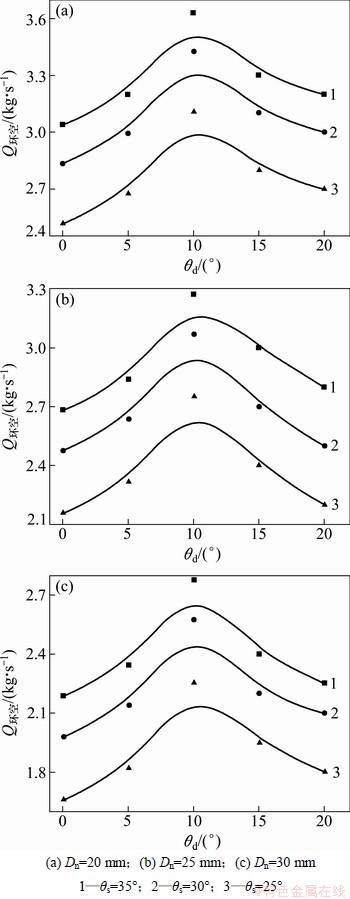
图10 θs变化时,Q环空随θd的变化规律
Fig. 10 Effect of θd on Q环空 at different θs
因为当喷嘴产生一定偏转角度后,压缩气体在经过喷嘴高速喷出后会沿着芯管内壁螺旋状上升,增加引射流对外环空空气的抽吸效果。当偏转角度增大到一定角度后,喷嘴喷出的高速气流会在芯管内壁产生碰撞干扰,并在芯管内形成紊流,从不利于引射流卷吸外环空的气体上返。
因此,在气力反循环钻头结构参数设计时,喷嘴偏转角度θd尽量选10°。
4.6 喷嘴数量N、喷嘴直径Dn变化时,引导段直径Dg对Q环空的影响规律
图11所示为喷嘴数量N、喷嘴直径Dn变化时,Q环空随Dg的变化规律。从图11可见:当Dn和Dg一定,N变化时,Q环空的数值波动剧烈;N和Dn一定时,随着Dg由35 mm增大到55 mm,Q环空数值先缓慢增加在减小。在不同Dn和N参数组合下,Dg在50 mm附近时,Q环空均取得最优值。
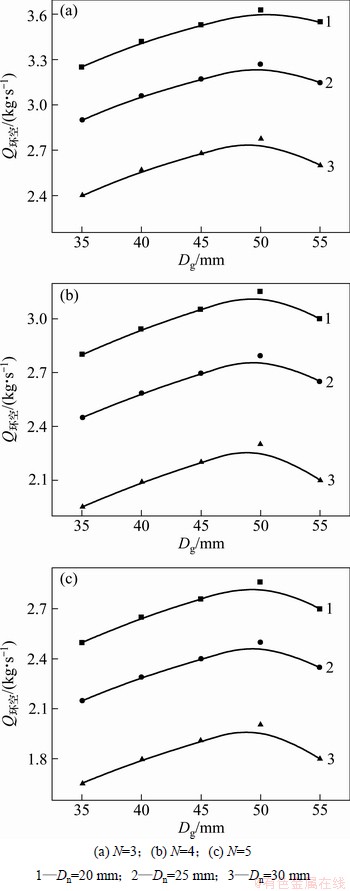
图11 Dn变化时, Q环空随Dg的变化规律
Fig. 11 Effect of Dg on Q环空at different Dn
这是因为引射流的卷吸能力主要受引射流体所携带的能量和流速影响,压缩气体通过引导段进入喷嘴时,引导孔直径过小,将增大引导孔内沿程损失,减弱引射流体卷吸能力;但引导孔直径增大,引射流体流速会降低,也会减弱引射流体对被引射流体的的卷吸能力。
因此,为使反循环形成效果达到最佳,在实际钻头结构参数设计中,Dg应尽量靠近50 mm。
5 结论
(1) 将引射器原理应用到大直径潜孔锤气力反循环钻头结构是可行的,并可实现稳定的反循环效果。
(2) 通过正交试验设计方法,得到钻头6个结构参数的主次因素和最优水平,优选出了最优理论参数组合。钻头6个结构参数显著影响目标值Q环空,L8(27)与L18(37)正交表中各因素的主次顺序一致,它们对目标值Q环空影响由大至小的顺序是:喷嘴直径Dn,喷嘴数量N,喷嘴偏转角度θd,喷嘴倾斜角度θs,引导段直径Dg,喷嘴长度L。
(3) 当GQF-16潜孔锤供风量为50 m3/min,钻头直径为1.2 m时,喷嘴直径Dn=20 mm,喷嘴数量N=3,喷嘴偏转角度θd=10°,喷嘴倾斜角度θs=35°,引导段直径Dg=50 mm,喷嘴长度L=50 mm为最优理论参数组合,此时Q环空=3.575 kg/s,均大于L18(37)正交表中任意参数组合的Q环空,并且这组参数组合不在L18(37)正交表中。
参考文献:
[1] 肖宏彬. 竖向荷载作用下大直径桩的荷载传递理论及应用研究[D]. 长沙: 中南大学土木工程学院, 2005: 1-15.
XIAO Hongbin. Theoretical and application research on load transfer of vertically loading large diameter piles[D]. Changsha: Central South University, School of Civil Engineering, 2005: 1-15.
[2] Sethi P L, Geng I, Wong P K. Construction of rock socketed piles in-sydney sandstone to meet performance requirements[J]. Australian Geomechanics Journal, 2012, 47(3): 97-102.
[3] 王方, 杨智, 李夕兵. 山坡地上大体量建筑嵌岩桩基设计与施工[J]. 中南大学学报: 自然科学版, 2004, 35(3): 484-489.
WANG Fang, YANG Zhi, LI Xibing. The design and construction of rock-socketed pile of large building on hillside[J]. Journal of Central South University: Science and Technology, 2004, 35(3): 484-489.
[4] 谭现锋, 朱学顺, 胡克祯, 等. 潜孔锤旋挖钻机组合在基岩桩施工中的应用[J]. 探矿工程: 岩土钻掘工程, 2006, 7(3): 22-26.
TAN Xianfeng, ZHU Xueshun, HU Kezhen, et al. Down the hole hammer combined with auger drill in the pile of rock foundation[J]. Exploration Engineering: Rock & Soil Drilling and Tunneling, 2006, 7(3): 22-26.
[5] Kirk G, Muzondo T, Harney D. Improved grade control using reverse circulation drilling at Mogalakwena Platinum mine, South Africa[C]//Proceedings of 8th International Mining Geology Conference 2011. Australia: Australasian Institute of Mining and Metallurgy, 2011: 329-340.
[6] Bo K, Wang M S, Zhao Z Q. Numerical simulation on bottom hole flow fields of reverse circulation bit[J]. Applied Mechanics and Materials, 2012, 256/257/258/259: 2826-2830.
[7] Lyous C W, Bayum G. Air and gas drilling manual[M]. Second Edition. USA: McGraw-Hill Companies, 2001: 85-96.
[8] 朴金石, 殷琨, 赵志强, 等. 冲击回转钻进条件下硬质合金钻头柱齿磨损机理[J]. 吉林大学学报: 地球科学版, 2011, 41(1): 195-199.
PIAO Jinshi, YIN Kun, ZHAO Zhiqiang, et al. Wear mechanism of the rock drill buttons in the DTH hammer drill[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(1): 195-199.
[9] 张鲲鹏, 薛飞, 潘卫明, 等. 高压气体引射器的试验研究和仿真[J]. 热科学与技术, 2004, 3(2): 133-138.
ZHANG Kunpeng, XUE Fei, PAN Weiming, et al. Experimental investigation and numerical simulation of high-pressure gas ejector[J]. Journal of Thermal Science and Technology, 2004, 3(2): 133-138.
[10] 刘益才, 曹立宏, 马卫武, 等. 冰箱喷射器最优喷射系数分析[J]. 中南大学学报: 自然科学版, 2009, 40(2): 329-333.
LIU Yicai, CAO Lihong, MA Weiwu, et al. Optimum eject-coefficient of refrigerator-ejector[J]. Journal of Central South University: Science and Technology, 2009, 40(2): 329-333.
[11] Yadav R L, Patwardhan A W. Design aspects of ejectors: Effects on suction chamber geometry[J]. Chemical Engineering Science, 2008, 63(15): 3886-3897.
[12] Lucas C, Koehler J, Schroeder A, et al. Experimentally validated CO2 ejector operation characteristic used in a numerical investigation of ejector cycle[J]. International Journal of Refrigeration, 2013, 36: 881-891.
[13] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004: 61-165.
WANG Fujun. Computational fluid dynamics analysis[M]. Beijing: Tsinghua University Press, 2004: 61-165.
[14] 林建忠, 阮晓东, 陈邦国, 等. 流体力学[M]. 1版. 北京: 清华大学出版社, 2005: 76-95.
LIN Jianzhong, RUAN Xiaodong, CHEN Bangguo, et al. Fluid mechanics[M]. 1st ed. Beijing: Tsinghua University Press, 2005: 76-95.
[15] 范黎明, 殷琨, 张永光, 等. 基于引射原理的侧吸式反循环钻头结构参数数值研究[J]. 中南大学学报: 自然科学版, 2011, 42(1): 220-226.
FAN Liming, YIN Kun, ZHANG Yongguang, et al. Numerical investigation of geometry parameters onside-ejector DTH hammer RC bit[J]. Journal of Central South University: Science and Technology, 2011, 42(1): 220-226.
[16] 刘建林. 气体钻井用贯通式潜孔锤关键技术研究[D]. 长春: 吉林大学建设工程学院, 2009: 103-117.
LIU Jianlin. Researches on the key technologies of hollow-through DTH used in gas drilling[D]. Changchun: Jilin University, College of Construction Engineering, 2009: 103-117.
[17] 李云雁, 胡传荣. 试验设计与数据处理[M]. 1版. 北京: 化学工业出版社, 2008: 124-159.
LI Yunyan, HU Chuanrong. Experiment design and data processing[M]. 1st ed. Beijing: Chemical Industry Press, 2008: 124-159.
[18] 邓姝皓, 龚竹青, 易丹青, 等. 电沉积制备铁-镍-铬纳米晶合金箔工艺的正交设计[J]. 中南大学学报: 自然科学版, 2005, 36(6): 24-29.
DENG Shuhao, GONG Zhuqing, CAI Yiqing, et al. Orthogonal design of technology for electrodeposition nanocrystalline Fe-Ni-Cr alloy foil[J]. Journal of Central South University: Science and Technology, 2005, 36(6): 24-29.
[19] Franek L, Jiang X Y. Orthogonal design of experiments for parameter learning in image segmentation[J]. Signal Processing, 2013, 96: 1694-1704.
(编辑 邓履翔)
收稿日期:2013-04-01;修回日期:2013-06-29
基金项目:中国地质调查局资助项目(1212011120256)
通信作者:殷琨(1952-),男,吉林长春人,教授,从事多工艺冲击回转钻探工艺及工具研究;电话:13804320251;E-mail:yinkun@jlu.edu.cn