J. Cent. South Univ. (2012) 19: 1570-1576

DOI: 10.1007/s11771-012-1178-z

Efficient multiuser detector based on box-constrained dichotomous coordinate descent and regularization

QUAN Zhi(全智)^{1, 2}, LIU Jie(刘杰)³

1. Department of Electrical Engineering, Federal University of Juiz de Fora, Juiz de For a 36036900, Brazil;

2. School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China;

3. RF Engines Limited, Newport P0305WB, United Kingdom

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: The presented iterative multiuser detection technique was based on joint deregularized and box-constrained solution to quadratic optimization with iterations similar to that used in the nonstationary Tikhonov iterated algorithm. The deregularization maximized the energy of the solution, which was opposite to the Tikhonov regularization where the energy was minimized. However, combined with box-constraints, the deregularization forced the solution to be close to the binary set. It further exploited the box-constrained dichotomous coordinate descent algorithm and adapted it to the nonstationary iterative Tikhonov regularization to present an ef?cient detector. As a result, the worst-case and average complexity are reduced down as K^2.8 and K^2.5 floating point operation per second, respectively. The development improves the “efficient frontier” in multiuser detection, which is illustrated by simulation results. In addition, most operations in the detector are additions and bit-shifts. This makes the proposed technique attractive for fixed-point hardware implementation.

Key words: dichotomous coordinate descent; de-regularization; low complexity; multiuser detection; Tikhonov regularization

1 Introduction

In code division multiple access (CDMA) systems, multiuser detection was capable of providing high detection performance [1]. However, the complexity of multiuser detectors that were capable of approaching the optimal performance was still a very important issue. The comparison of advanced multiuser techniques in  Ref. [2], in terms of group detection error and complexity, had shown that an “efficient frontier” of multiuser detectors was primarily composed of the decision- feedback (DF) detector [3], probabilistic data association (PDA) detector [4], and branch and bound (BB) detector [5]. The DF detector was the simplest one; the BB detector provided the best detection performance, while the PDA detector gave a good detection performance with simpler implementation than the BB detector [2]. An iterative multiuser detection technique based on box-constrained solution with Gauss-Seidel iterations and nonstationary iterative deregularization (GS-BD) had been proposed in Ref. [6]. This multiuser detection was based on the iterated Tikhonov regularization [7]. In  Ref. [6], the algorithm exploited the advantages of the bootstrap detector [8] and technique of deregularization. However, the deregularization maximized the energy of the solution, in opposite to minimizing it in the Tikhonov regularization. Combined with box-constraints, the deregularization forced the solution to be close to the binary set and improved the “efficient frontier” with the complexity as low as K^3.2 floating point operation per second (FLOPS).

It further developed the GS-BD technique by exploiting the box-constrained dichotomous coordinate descent (DCD) algorithm and adapted it to the nonstationary iterative Tikhonov regularization to present the DCD-BTN (DCD box constraint with negative diagonal loading and Tikhonov iterations) detector [9]. As a result, the worst-case and average complexity were reduced down to K^2.8 and K^2.5 FLOPS, respectively. Although only the multiuser detection problem was addressed here, the algorithm was applicable to a wide class of applications since many communication problems can be formulated as quadratic optimization with similar constraints. Moreover, most operations in the detector were additions and bit-shifts. This made the proposed technique attractive for fixed-point hardware implementation.

2 Problem formulation of multiuser detection

The matched-filter output at a symbol synchronous CDMA receiver is given by the K-length vector:

θ=Rh+n                                    (1)

where the vector h{-1, +1}^K, contains bits transmitted by the K users, R is a positive definite signature waveform correlation K×K matrix, and n is a real-valued zero-mean Gaussian random vector with covariance matrix σ²R. The Eq. (1) also describes multiuser communications in multi-antenna, ?at and frequency- selective fading channels [10]. The multiple input multiple output (MIMO) communication [11-12] and other communication scenarios [13-15] can also be modeled by Eq. (1).

The optimal maximum likelihood (ML) multiuser detector estimates the vector h by minimizing the following quadratic function with binary constraints h{-1, +1}^K:

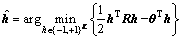                (2)

Although the ML detector provides the best detection performance, it is not practical due to its high complexity.

3 Non-stationary iterative Tikhonov regula- rization

The minimum mean square error (MMSE) detector solves the unconstrained quadratic optimization problem [1] using the regularization term (λ/2)h^Th:

            (3)

where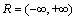. This regularization was also known as diagonal loading [16], which promotes a solution with a small energy. A more accurate solution to the problem (Eq. (2)) could be obtained using the non-stationary Tikhonov iterative regularization [17-18]. Instead of solving (Eq. (3)), a sequence of (N+1) unconstrained optimization problems could be solved, with the n-th unconstrained optimization problem:

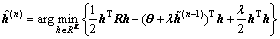 (4)

where n (=0, …, N) is the Tikhonov iteration index, 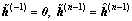 and λ>0.

The solution of Eq. (4) could be regarded as an unconstrained solution to the following equation:

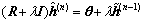                      (5)

When N=0, it obtains the MMSE detector where the final solution is 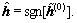 When N≥1, the described multiuser detector provides a better performance than the MMSE detector [8], and in this case, the final solution is given by the hard decision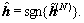

As proposed in Ref. [8], λ varies with n according to

                       (6)

In Eq. (5),  is a semi-hard version of  for which the k-th element is given by [8]

                        (7)

where α<0 is a pre-defined coefficient.

Obtaining a direct solution of Eq. (5) requires approximately K³ FLOPS. Consequently, a direct implementation of the detector with N Tikhonov iterations requires (N+1)K³ FLOPS. In the simulation below, this direct implementation is called Direct-T detector. This detector achieved a good detection performance [6]; however, its complexity is high.

In order to reduce the complexity, Eq. (5) could be solved approximately using the classical Gauss-Seidel (GS) iterations [6]. In most cases, the GS iterations could significantly reduce the detector complexity without a significant degradation in performance. The detector using GS iterations is called as GS-T detector. The GS-T detector approached the “efficient frontier”, but does not improve it.

4 Detectors with box-constrained relaxation

The complicated optimization problem (Eq. (2)) could be approximately solved by relaxing the binary constraint h{-1, +1}^K. A multiuser detector with sphere constraint provides a detection performance similar to that of the MMSE detector [19]. Using the box-constraint h{-1, +1}^K results in a better performance than the sphere-constrained minimization [2, 19-20]. A multiuser detector with box-constraint solves the convex optimization problem by

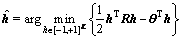                (8)

The solution to Eq. (8) could be regarded as a box-constrained solution to

Rh=θ                                       (9)

The Eq. (9) could be solved by nonlinear GS iterations [21]. Each iteration consists of two steps. At the first step, the classical GS iteration was performed as

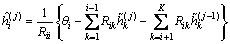        (10)

where j=1, …, N_GS, is the iteration index;  and are elements of vectors  and 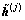, respectively;  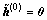and R_ik is the (i, k)-th element of the matrix R. At the second step, the semi-hard update is performed as

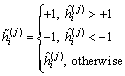                        (11)

The final solution is obtained by applying the hard decision: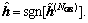

The complexity of Eq. (10) with N Tikhonov iterations is 2(N+1)N_GSK² FLOPS. To simplify the algorithm further, when solving Eq. (5) for the (n+1) Tikhonov iteration, the GS iteration is initialized with the semi-hard solution Eq. (7) obtained from the n-th Tikhonov iteration. When the initial value is close to the equilibrium, the number of GS iterations for solving    Eq. (5) can be significantly reduced. However, to ensure an accurate solution,  GS iterations for the first step are used, which solve the classical MMSE detection problem, and 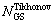 GS iterations are used for other updated. The overall complexity of the algorithm was  FLOPS.

Algorithm 1: Box-constrained DCD algorithm

Initialization:  H=1, p=0.

for m=1:M_b

Step 1: d=2^-m+1

Step 2: Flag=0, …, pass

Step 3: for j=1:K …iteration

Step 4:   if |r(j)|>(d/2)R(j, j) then

Step 5:     x=h(j)+sgn(r(j))d

Step 6:     if |x|≤H then

Step 7:       h(j)=x

Step 8:       r=r-sgn(r(j))·d·R(:, j)

Step 9:       Flag=1, p=p+1

Step 10:      if p>N_u end algorithm

Step 11: end j-loop

Step 12: if Flag=1, go to Step 2

end m-loop.

The box-constrained dichotomous coordinate descent (DCD)-based multiuser [22-23] uses the box- constraint h[-1, +1]^K in the quadratic minimization (Eq. (2)). Algorithm 1 presents the box-constrained DCD algorithm. The box-constrained DCD algorithm is designed to offer a simple solution for the vector h, without explicit multiplications and divisions. The final accuracy of the solution vector h depends on the number of bits (M_b), the number of iterations, and the conditional number of the system matrix. The first set of iterations in the algorithm determines the most significant bit (m=1) for all elements of h using a step size parameter d. The subsequent sets of iterations determine the less significant bits up to a suitable number of bits (maximally M_b). The residual vector is given by 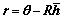, where  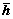is the initialization of h. In this work,  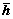is set to be zero, and r is equal to θ. The step-size d is reduced by power of two at Step 1, so no explicit multiplication or division is carried out as all the multiplications and divisions could be replaced by simple bit shifts. If an element of the solution vector is updated at iteration, such iteration is labeled “successful”. For every step size update, the algorithm repeats successful iterations until all elements of the residual vector r becomes so small that the condition at Step 4 is not met for all j or h over?ows the range [-H, +H] at Step 6, where H=1 for BPSK modulation. The computational load of the algorithm mainly depended on these successful iterations N_u and the number of bits M_b. A limit for the number of successful iterations N_u could be predefined and used as a stopping condition (at Step 10). If there is no such limit, or the limit is high enough, the accuracy of the solution is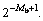

The coordinate descent iterations used by the box- constrained DCD algorithm could also solve Eq. (9).

5    Nonstationary Tikhonov iterations with box-constraint and negative diagonal loading

The regularization with negative loading is given, and it is justified by using the regularization together with the box-constraint. Then, the detector that performs Tikhonov iterations with such regularization and box-constraint are introduced. Finally, the proposed DCD based detector could be further simplified by exploiting inherent properties of DCD algorithm.

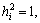The box-constraint tightens the solution set, which results in a better detection performance compared to that with the unconstrained solutions. An additional tightening of the solution could further improve the performance. The binary constraint h{-1, +1}^K implies that  where h_i is the i-th element of the vector h, hence, h^Th=K. Within the K dimensional box [-1, +1]^K, the solution h satisfies the inequality (K-h^Th)≥0. Therefore, for forcing the vector h[-1, +1]^K to be close to the binary set h{-1, +1}^K, it needs to minimize the term (K-h^Th). Thus, an additional tightening of the solution set could be achieved by introducing the following optimization problem:

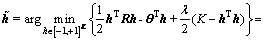
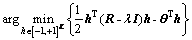                     (12)

where λ>0. The solution in Eq. (12) could be considered as a box-constrained solution to

(R-λI)h=θ                                       (13)

The matrix R in Eq. (9) was replaced by the matrix (R-λI), which implies that the joint box-constraint and regularization with negative diagonal loading are used. The regularization parameter λ is chosen as that in the MMSE detector, i.e. λ=σ². The final solution  is obtained by projecting the vector  to the binary set as =sgn[]. The solution to Eq. (13) could be found either by using nonlinear GS iterations in Ref. [6] or by using the DCD algorithm with the matrix R replaced by (R-λI). The GS iterations with box-constrained and negative diagonal loading (GS-BN) detector use the orthogonal projection operation to perform the semi-hard update. In the DCD box constrained detector, the projection is not used. Instead, before deciding whether an iteration is “successful” or “unsuccessful”, the box-constraint test is applied to a possible solution (i.e. pre-update of h). If the possible solution is outside the box, the iteration is considered as “unsuccessful” and the update is cancelled. Consequently, it obtains the GS-BN or DCD box- constrained negative loading (DCD-BN) detectors with improved performance compared to the box-constrained multiuser detectors.

The Tikhonov iterations are taken into account. At zero Tikhonov iteration, the optimization problem    (Eq. (12)) that corresponds to the GS-BN or DCD-BN detectors is solved. In further Tikhonov iterations, the solution of the optimization problem could be found:

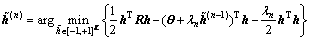                (14)

which could be considered as a box-constrained solution of

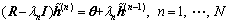        (15)

The regularization parameter λ_n is determined as that in Eq. (6). The final solution is obtained by using the hard decision 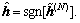 The Eq. (15) could be solved either by the GS iterations or the DCD algorithm. Consequently, the GS-Box constraint with negative diagonal loading and Tikhonov iterations (GS-BTN) or DCD-Box constraint with negative diagonal loading and Tikhonov iteration (DCD-BTN) detectors is obtained.

So far, it is assumed that the box-constrained DCD algorithm is implemented with zero-initialization of the solution vector h and an initialization of the residual vector as r=θ. However, a non-zero initialization vector h can also be used, for which the initialization of the residual vector becomes as r=θ-Rh. If the initialization vector h is close to the final solution, the number of “successful” updated in the box-constrained DCD algorithm could be reduced, resulting in a reduction in the complexity. For the proposed DCD-BTN detector, and after each Tikhonov iteration, the accuracy of the solution is improved in general. So, it could be used for initializing the vector h in the following Tikhonov iteration. It is expected that with such initialization, the complexity of the box-constrained DCD algorithm decreases as n increases.

However, it also requires extra 2NK² FLOPS for initialization of the residual vector in the N Tikhonov iterations, which could be substantial for a large N. To avoid this complication, zero initialization is applied for h (i.e. θ initialization is used for r) in the box-constrained DCD algorithm, where the solution 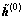 and the residual vector r⁽⁰⁾ would be used later in the Tikhonov iterations of the DCD-BTN algorithm. The DCD-BTN detector could be implemented according to the following steps:

Step 1: Solve the equation (R-λ₀I)h=θ by using the box-constrained DCD algorithm with the zero- initialization of h and matrix R is replaced by (R-λ₀I), i.e. using DCD-B (0, R-λ₀I, θ, H, N_u, M_b), to obtain a solution vector 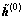 and a residual vector r⁽⁰⁾.

Step 2: For n=1, …, N, solve Eq. (15) by using the box-constrained DCD algorithm with  as an initialization of the solution.

Step 3: Apply the hard decision to 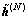 to obtain the final solution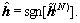

6 Simplified implementation of DCD-BTN multiuser detector

In the DCD-BTN detector, at the zero Tikhonov iteration, the equation (R-λ₀I)h=θ is solved with respect to h by using the DCD algorithm with zero-initialization of the solution vector and initialization of the residual vector r by the vector θ. The DCD algorithm provides a solution vector 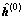 and the residual vector:

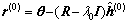                       (16)

If at the first Tikhonov iteration, the vector 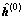 is used for initialization of the solution vector of the equation, the residual vector r should be initialized by the vector:

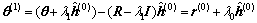        (17)

where the last equality is due to Eq. (16). The DCD algorithm produces a solution vector h⁽¹⁾ and the residual vector:

                 (18)

At the 2nd Tikhonov iteration, it solves the problem 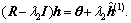 For initializing the solution of this equation by the vector 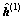, it also initializes the residual vector r by the vector:

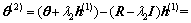
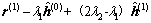               (19)

where the last equality is due to Eq. (18). The DCD algorithm produces a solution vector 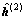 and the residual vector  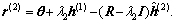Similarly, at the (n-1)-th Tikhonov iteration, n≥3, the DCD algorithm produces a solution vector  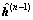and the residual vector:

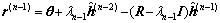         (20)

At the n-th Tikhonov iteration, n≥3, it solves the problem 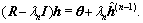 For initializing the solution by the vector 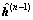, it also initializes the residual vector r by the vector:

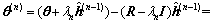
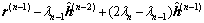       (21)

where the last equality is due to Eq. (20). Combining  Eqs. (17), (19) and (21) together, the following equation could be obtained:

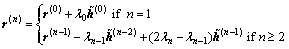                (22)

As an initialization of the residual vector, matrix R is replaced by R-λ_nI, i.e. using DCD-B 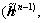 R-λ_nI, r⁽ⁿ⁾, H, N_u, M_b) to obtain a solution vector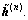

7 Simulation results

The numerical results are presented to show the detection performance and complexity of the DCD-BTN multiuser detector. The same simulation environment (AWGN channel) is used, with randomly generated binary spreading codes and highly loaded scenarios as those in Ref. [2]. For the box-constrained DCD algorithm, the maximum number of successful iterations N_u=1 000 is used. Although using a smaller N_u can reduce the complexity of the algorithm with little degradation in performance, it sets N_u at a high value to ensure the best detection performance.

The proposed DCD-BTN algorithm is further compared with the “efficient frontier” presented in   Ref. [2]. It uses a highly loaded scenario, for which the number of users K=60 and the spreading factor (SF) is 63. Figure 1 shows the group detection error (probability of at least one error among all K user data) as a function of the detector worst-case complexity for signal-to-noise ratio (SNR) of 10 dB. The known BB, PDA, and DF detectors form the “efficient frontier”, i.e. they provide the best trade-off in terms of the complexity and detection performance. The Direct-T detector exploits the non-stationary Tikhonov iterative regularization as described in Ref. [8]. The case of N=0 corresponds to the MMSE detector whose performance is poor. As N increases, the detection performance significantly improves, but is still worse than that of the BB detector. The performance improvement with respect to the MMSE detector is achieved at the expense of an increase in the complexity. The simulations were run for high N beyond 30, but the performance is not improved, and is still worse than that of the BB detector. The results marked ‘GS-T’ are related to the GS implementation of the detector using Tikhonov iterative regularization as described in Ref. [6]. Within each Tikhonov iteration, GS iterations reduce the complexity without degrading the detection performance. However, even with GS iterations, the detector cannot improve the “efficient frontier”.

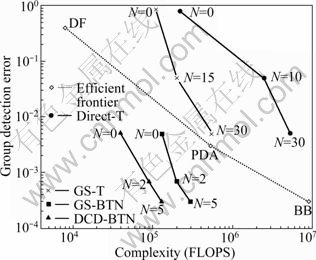
Fig. 1 Group detection error versus worst-case complexity (K= 60; SF: 63; SNR: 10 dB)

The GS-BTN detector that uses GS iterations to implement Tikhonov regularization with negative diagonal loading and box-constraint outperforms the GS-T detector in terms of the group detection error. When N=5, the GS-BTN detector achieves the same performance as that of the BB detector, which also presents the optimal ML detection performance.

Compared to the Direct-T and GS-T detectors, the GS-BTN detector allows a significant improvement in the detection performance. It also allows a reduction in the required number of Tikhonov iterations (to achieve the best reached performance) from N=30 to N=5, which results in a lower complexity. The complexity of the GSBTN detector is as low as approximately K^3.2 FLOPS (When the simulations are run, the corresponding complexity can also be calculated).

The DCD-BTN detector also achieves the lowest group detection error after N=5 Tikhonov iterations. Its performance is similar to that of the GS-BTN detector. However, the worst-case complexity of the DCD-BTN detector with N=5 Tikhonov iterations is only K^2.8 FLOPS, which is lower than that of the GS-BTN detector. Thus, the DCD-BTN detector allows the reduction in the worst-case complexity, compared to the GS-BTN detector without degrading the detection performance.

Figure 2 shows the group detection error as a function of the average complexity for the case that K is 60, SF is 63 and SNR is 10 dB. The DCD-BTN detector has a lower average complexity than other detectors. The only exception is the DF detector, but its detection performance is poor. Moreover, the DF detector requires computing the Cholesky decomposition of the matrix R (not taken into account in Figs. 1 and 2). For N=5, the DCD-BTN detector achieves the same detection performance as the BB detector, i.e. it achieves the performance of the optimal ML detector. In this case, the average complexity of the DCD-BTN detector is approximately K^2.5 FLOPS, which is lower than that of the BB detector.

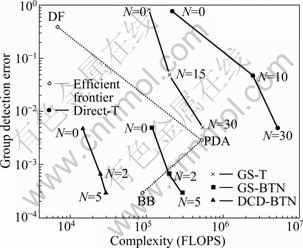
Fig. 2 Group detection error versus average complexity (K=60; SF: 63; SNR: 10 dB)

Figure 3 demonstrates the group detection error of the BB and DCD-BTN detectors as a function of the worst-case complexity for the case that K is 60, SF is 63 and SNR is 7 dB. Simulation results are shown for a BB detector with upper bounded complexity for several complexity bounds (5×10⁵, 10⁶ and 5×10⁶). This is due to the high worst-case complexity of the BB detector for low SNRs. The detection performance of the DCD-BTN is significantly better than that of the BB detector. In addition, the complexity of the DCD-BTN detector is significantly lower than that of the BB detector.

Figure 4 shows the bit error rate performance of the detectors DF, PDA and DCD-BTN with N=5 compared to the single-user bound as a function of SNR for the case the K is 60 and SF is 63. It can be seen that the DCD-BTN detector outperforms the other detectors, especially at high SNRs. In this case, its BER performance is close to that of the single user bound.

Fig. 3 Group detection error vs worst-case complexity (K=60; SF: 63; SNR: 7 dB)

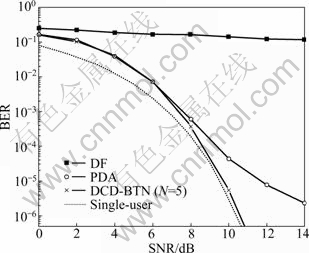
Fig. 4 BER performance of DF, PDA, and DCD-BTN detectors against single-user bound (K=60; SF: 63)

The DCD-BTN multiuser detector has the lowest complexity among detectors providing the ML performance. It significantly improves the “efficient frontier” in multiuser detection. An extra benefit of the proposed DCD-BTN detector is that it is essentially multiplication-free and division-free. Multiplications are only required for calculation of the vector r⁽ⁿ⁾ and diagonal elements of the matrix in Eq. (15). Most operations in the detector are additions and bit-shifts. This makes the proposed technique attractive for fixed-point hardware implementation [24-28].

8 Conclusions

1) A known iterative multiuser detection technique based on box-constrained solution with GS-BN provides a better trade-off between complexity and detection performance than the “efficient frontier”, which is formed by the DF, PDA, and BB detectors. By using DCD iterations instead of the Gauss-Seidel iterations, the DCD-box constraint with negative diagonal loading and Tikhonov iterations multiuser detector is proposed.

2) The performance of the DCD-BTN detector, in terms of group detection error and complexity, has been compared with that of the existing advanced multiuser detection techniques, such as the DF, BB and PDA detectors. The DCD-BTN detector shows the lowest complexity among these detectors while provides almost an ML-like performance.

3) Most operations in the DCD-BTN detector can be implemented using additions and bit-shifts. This makes it easy for implementing in the real-time hardware. The multiplications are only required for calculation of the residual vector r update. However, this involves a very small number of multiplications.

References

[1] VERDU S. Multiuser detection [M]. Cambridge, UK: Cambridge University Press, 1998.

[2] HASEGAWA F, LUO J, PATTIPATI K, WILLETT P, PHAM D. Speed and accuracy comparison of techniques for multiuser detection in synchronous CDMA [J]. IEEE Trans Commun, 2004, 52(4): 540-545.

[3] VARANASI M K. Decision feedback multiuser detection: A systematic approach [J]. IEEE Trans Inform Theory, 1999, 45(1): 219-240.

[4] LUO J, PATTIPATI K R, WILLETT P K, HASEGAWA F. Near-optimal multiuser detection in synchronous CDMA using probabilistic data association [J]. IEEE Comm Letters, 2001, 5(9): 361-363.

[5] LUO J, PATTIPATI K, WILLETT P, BRUNEL L. Branch-and- bound-based fast optimal algorithm for multiuser detection in synchronous CDMA [C]// Proc IEEE Int Conf on Communications, ICC’2003. Anchorage, Alaska, USA, 2003: 3336-3340.

[6] ZAKHAROV Y V, LUO J, KASPARIS C. Joint box-constraint and deregularization in multiusr detection [C]// 14th European Signal Processing Conference. Florence, Italy, 2006: 1-5.

[7] ENGL H W. Necessary and sufficient conditions for convergence of regularization methods for solving linear operator equations of the first kind [J]. Numerical Functional Analysis and Optimization, 1981, 3(2): 201-222.

[8] KASPARIS C, PIECHOCKI R J, FLETCHER P N, NIX A R. A bootstrap multiuser detector for CDMA based on Tikhonov regularization [C]// Proc IEEE International Symposium Acoustic, Speed, and Signal Processing. Hong Kong: IEEE Press, 2003: 69-72.

[9] ZAKHAROV Y, LUO J, KASPARIS C. Efficient multiuser detection based on box-constraint relaxation, regularization with negative diagonal loading and coordinate-descent iterations [M]. Preprint, University of York, U.K. 2006.

[10] RASMUSSEN L K, ALEXANDER P D, LIM T J. A linear model for CDMA signals received with multiple antennas over multipath fading channels [C]// CDMA Techniques for Third Generation Mobile Systems. Norwell Kluwer Academic Publishers, 1999: 23-57.

[11] JENSEN M A, WALLACE J W. A review of antennas and propagation for MIMO wireless communications [J]. IEEE Trans Antennas and Propagation, 2004, 52(11): 2810-2824.

[12] VISHNU VARDHAN K, MOHAMMED S K, CHOCKALINGAM A, SUNDAR RAJAN B. A low complexity detector for large MIMO systems and multiuser CDMA systems [J]. IEEE Journal on Selected Areas in Communications, 2008, 26(3): 473-485.

[13] SPASOJEVIC P, GEORGHIADES C N. The slowest descent method and its application to sequence estimation [J]. IEEE Trans Commun, 2001, 49(9): 1592-1604.

[14] TEYAN C, ZAKHAROV Y V, CHUNSHAN L. Low complexity channel estimate based adaptive linear equalizer [J]. IEEE Signal Processing Letters, 2011, 18(7): 427-430.

[15] QUAN Z, RIBEIRO M V. A low cost STBC-OFDM system with improved reliability for power line communications [C]// 2011 IEEE International Symposium on Power Line Communications and Its Applications (ISPLC). New Jersey: IEEE Press, 2011: 261-266.

[16] VOROBYOV S A, GERSHAN A B, LUO Z Q. Robust adaptive beamforming using worst-case performance optimization: a solution to the mismatch problem [J]. IEEE Trans Signal Processing, 2003, 51(2): 313-324.

[17] NEUMAIER A. Solving ill-conditioned and singular linear systems: A tutorial on regularization [J]. SIAM Review, 1998, 40(3): 636- 666.

[18] HANKE M, GROETSCH C W. Nonstationary iterated Tikhonov regularization [J]. J Optim Theory Appl, 1998, 98(1): 37-53.

[19] TAN P H, RASMUSSEN L K, LIM T J. Box-constrained maximum-likelihood detection in CDMA [C]// Proc IEEE 51st Vehicular Technology Conf Spring2000. Tokyo, Japan: IEEE Press, 2000: 517-521.

[20] TAN P H, RASMUSSEN L K, LIM T J. Constrained maximum-likelihood detection in CDMA [J]. IEEE Trans Commun, 2001, 49(1): 142-153.

[21] YENER A, YATES R D, ULUKUS S. CDMA multiuser detection: A nonlinear programming approach [J]. IEEE Trans Commun, 2002, 50(6): 1016-1024.

[22] ZAKHAROV Y V, TOZER T C. Box-constrained multiuser detection based on multiplication-free coordinate descent optimization [C]// Proc Fifth IEEE Workshop on Signal Processing Advances in Wireless Communications. Lisboa, Portugal, 2004: 11-14.

[23] ZAKHAROV Y, TOZER T C. Multiplication-free iterative algorithm for LS problem [J]. Electronics Letters, 2004, 40(9): 567-569.

[24] LIU J, ZAKHAROV Y, WEAVER B. Architecture and FPGA design of dichotomous coordinate descent algorithms [J]. IEEE Trans Circuits and Systems. Part I: Regular Papers, 2009, 56(11): 2425- 2438.

[25] QUAN Z, LIU J, ZAKHAROV Y. FPGA design of box-constrained MIMO detector [C]// IEEE International Conference on Communications ICC 09. New Jersey: IEEE Press, 2009: 1-5.

[26] LIU J, WEAVER B, ZAKHAROV Y. FPGA implementation of multiplication-free complex division [J]. Electronics Letters, 2008, 44(2): 95-96.

[27] QUAN Z, LIU J, ZAKHAROV Y. FPGA implementation of DCD based CDMA multiuser detector [C]// 15th Int Conf on Digital Signal Processing. New Jersey: IEEE Press, 2007: 319-322.

[28] LIU J, QUAN Z, ZAKHAROV Y. Parallel FPGA implementation of DCD algorithm [C]// 15th Int Conf on Digital Signal Processing. New Jersey: IEEE Press, 2007: 331-334.

(Edited by DENG Lü-xiang)

Received date: 2011-07-14; Accepted date: 2011-10-09

Corresponding author: QUAN Zhi, PhD; Tel: 55-32-21023465; E-mail: zhi.quan@engenharia.ufjf.br